Опорный конспект Кор, УВТ, Мех, Эл, ТБ, СБ,ПТМ . 18-19

1.

Федеральное агентство морского и речного транспорта
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Волжский государственный университет водного транспорта»
Кафедра теории конструирования инженерных сооружений
Составители Н.А. Анисимова, И.Н. Шоркина
ЛЕКЦИОННО-ПРАКТИЧЕСКАЯ ТЕТРАДЬ
ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ И
ИНЖЕНЕРНОЙ ГРАФИКЕ
для студентов дневного отделения

2.

(специальностей 26.03.02 - Кораблестроение, 20.03.01 - Техносферная безопасность,
26.03.01- Управление водным транспортом, 08.03.01- Строительство,
26.05.06 - Эксплуатация судовых энергетических установок,
23.03.03 - Эксплуатация транспортно-технологических машин и комплексов)
Преподаватель
Студент
группа
Нижний Новгород
2018

3.

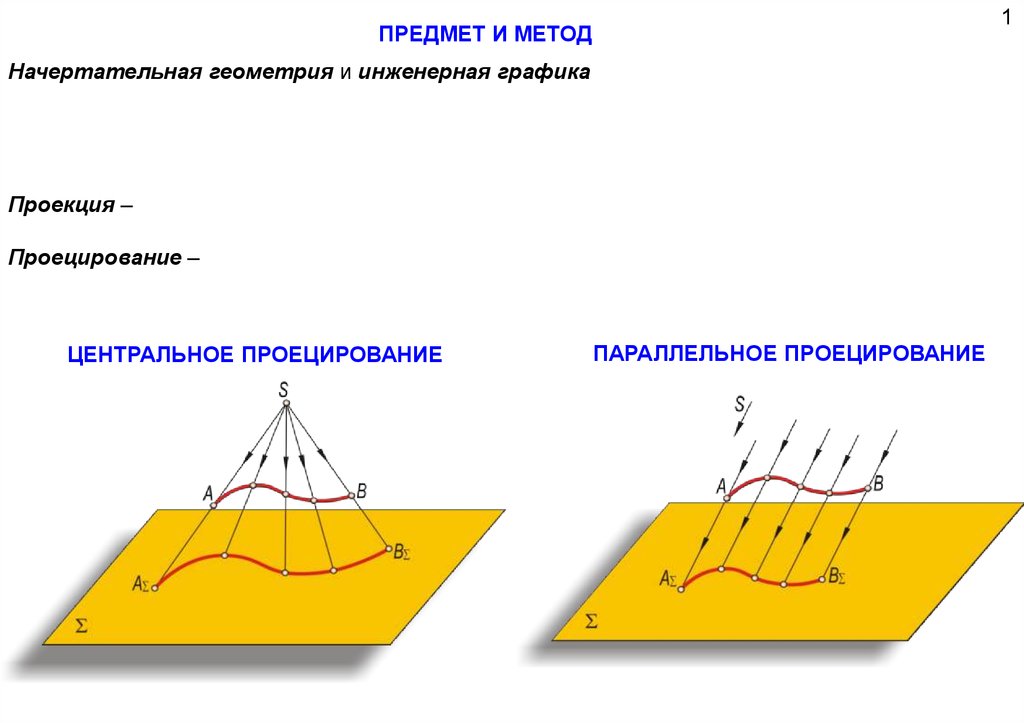
1
ПРЕДМЕТ И МЕТОД
Начертательная геометрия и инженерная графика
Основным методом построения изображений на плоскости является
метод проекций.
Проекция –
Проецирование –
ЦЕНТРАЛЬНОЕ ПРОЕЦИРОВАНИЕ
ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ

4.

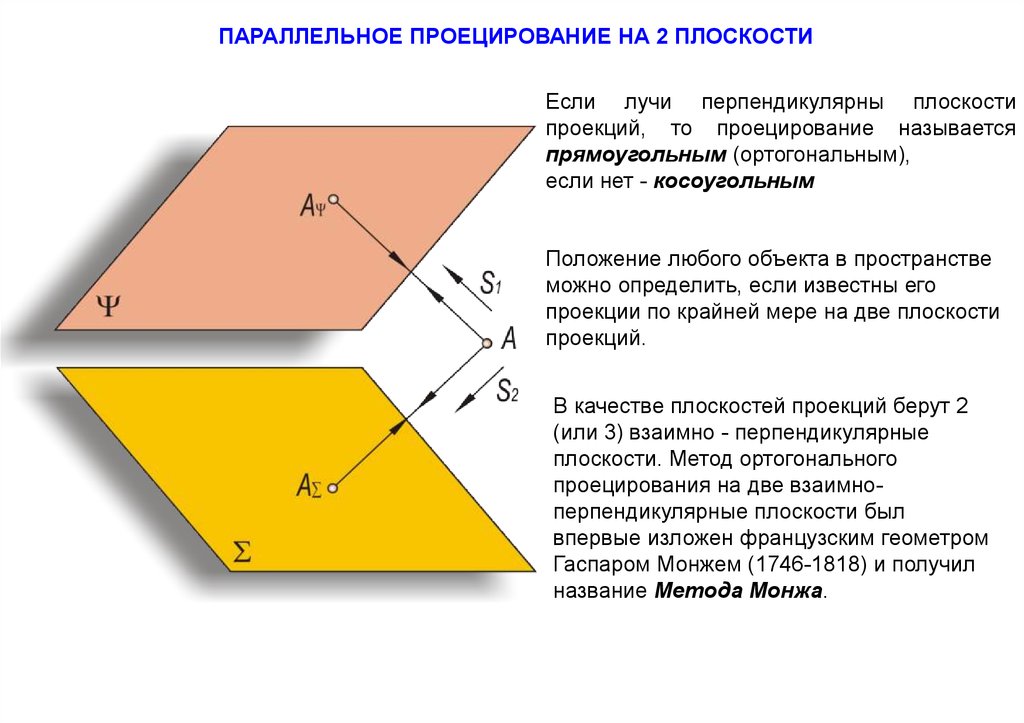
ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ НА 2 ПЛОСКОСТИ
Если лучи перпендикулярны плоскости
проекций, то проецирование называется
прямоугольным (ортогональным),
если нет - косоугольным
Положение любого объекта в пространстве
можно определить, если известны его
проекции по крайней мере на две плоскости
проекций.
В качестве плоскостей проекций берут 2
(или 3) взаимно - перпендикулярные
плоскости. Метод ортогонального
проецирования на две взаимноперпендикулярные плоскости был
впервые изложен французским геометром
Гаспаром Монжем (1746-1818) и получил
название Метода Монжа.

5.

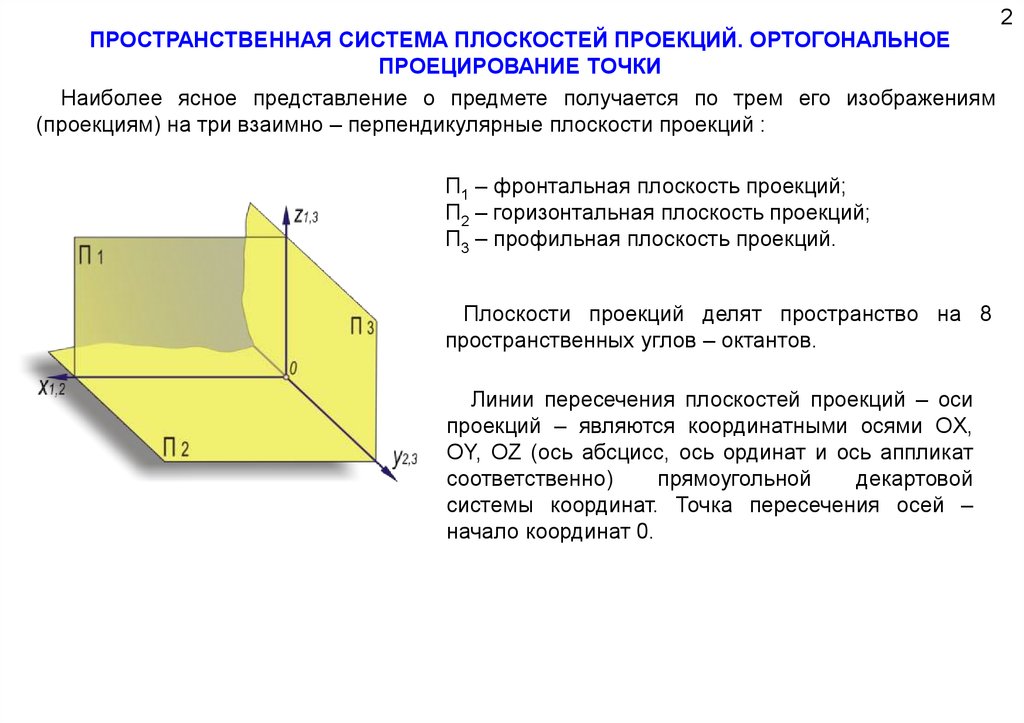
ПРОСТРАНСТВЕННАЯ СИСТЕМА ПЛОСКОСТЕЙ ПРОЕКЦИЙ. ОРТОГОНАЛЬНОЕ
ПРОЕЦИРОВАНИЕ ТОЧКИ
Наиболее ясное представление о предмете получается по трем его изображениям
(проекциям) на три взаимно – перпендикулярные плоскости проекций :
П1 – фронтальная плоскость проекций;
П2 – горизонтальная плоскость проекций;
П3 – профильная плоскость проекций.
Плоскости проекций делят пространство на 8
пространственных углов – октантов.
Линии пересечения плоскостей проекций – оси
проекций – являются координатными осями OX,
OY, OZ (ось абсцисс, ось ординат и ось аппликат
соответственно)
прямоугольной
декартовой
системы координат. Точка пересечения осей –
начало координат 0.
2

6.

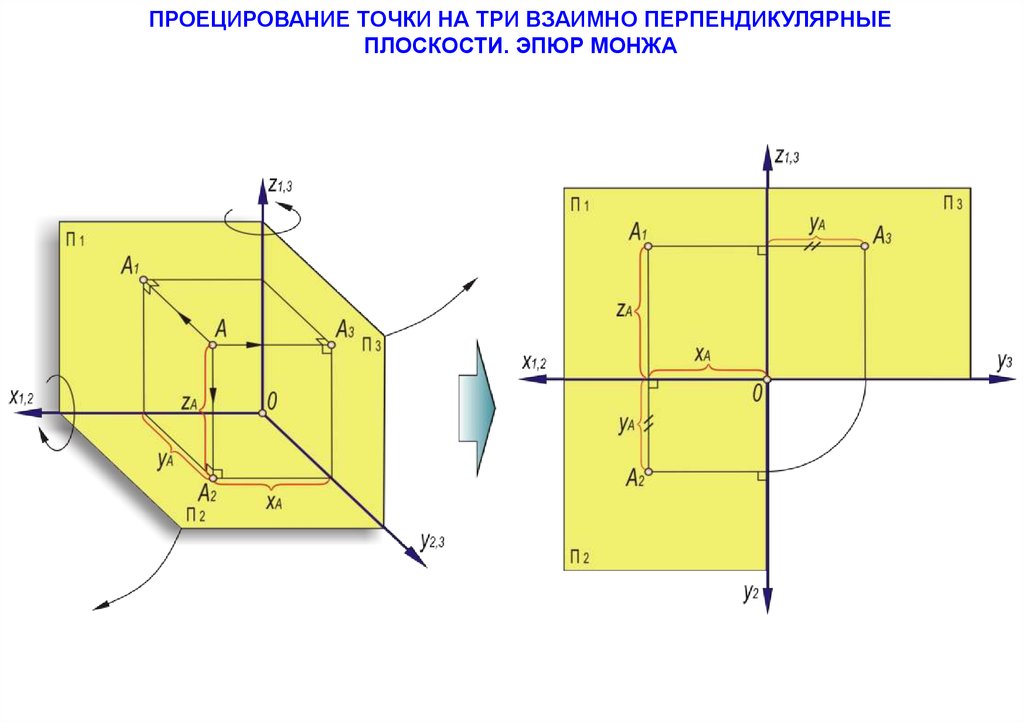
ПРОЕЦИРОВАНИЕ ТОЧКИ НА ТРИ ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫЕ
ПЛОСКОСТИ. ЭПЮР МОНЖА

7.

ЧАСТНЫЕ ПОЛОЖЕНИЯ ТОЧЕК НА ЧЕРТЕЖЕ
3

8.

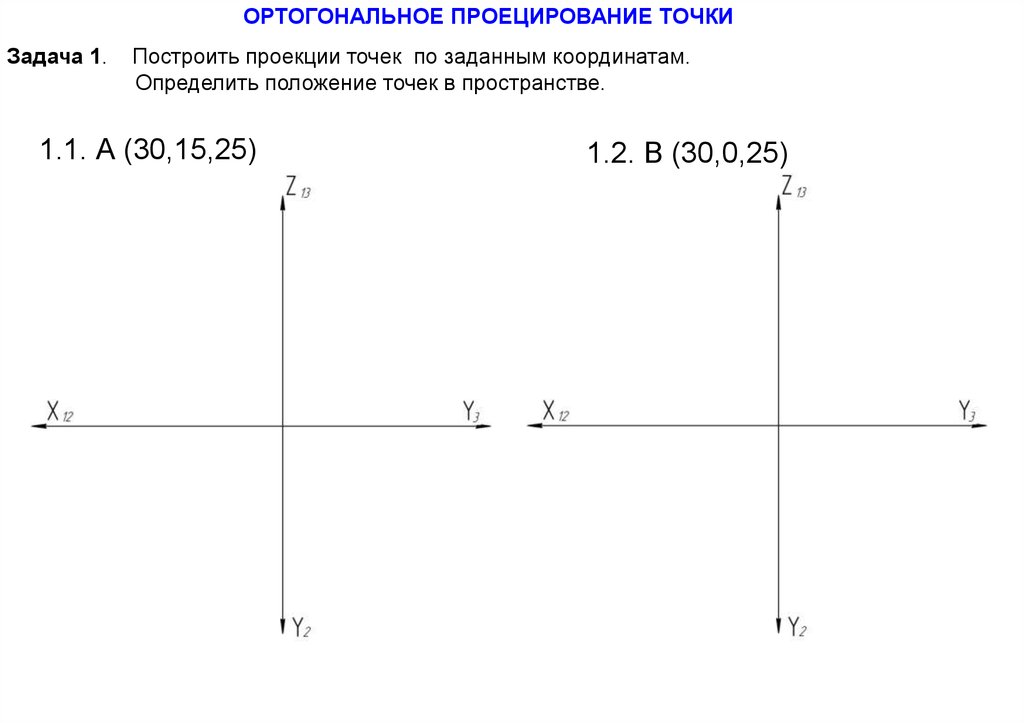
ОРТОГОНАЛЬНОЕ ПРОЕЦИРОВАНИЕ ТОЧКИ
Задача 1.
Построить проекции точек по заданным координатам.
Определить положение точек в пространстве.
1.1. А (30,15,25)
1.2. В (30,0,25)

9.

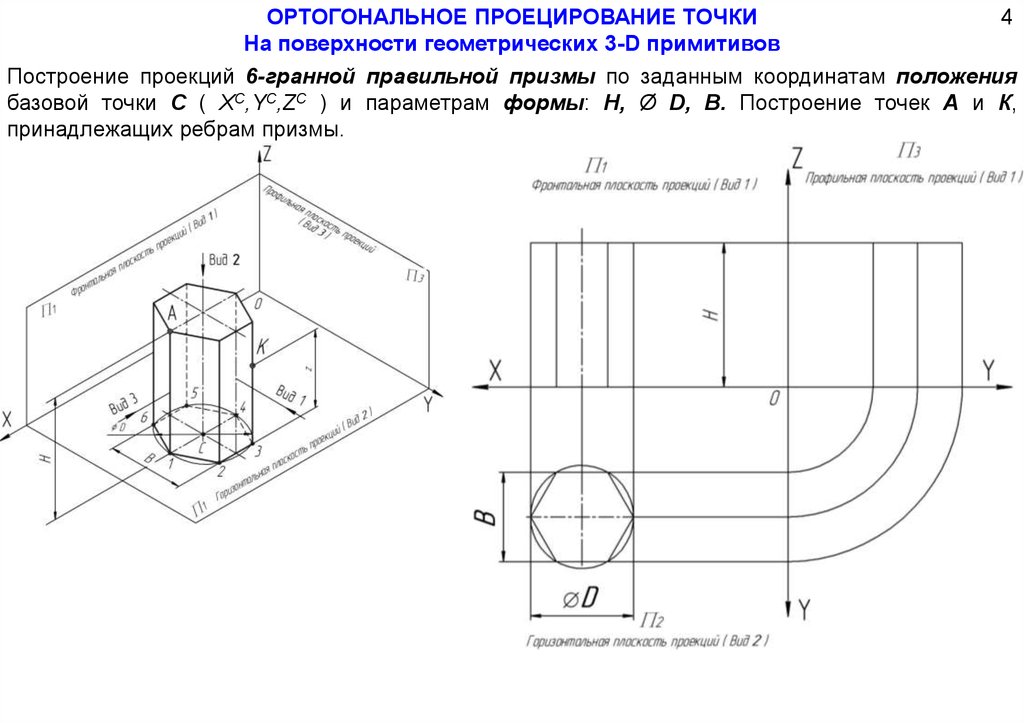
ОРТОГОНАЛЬНОЕ ПРОЕЦИРОВАНИЕ ТОЧКИ
На поверхности геометрических 3-D примитивов
4
Построение проекций 6-гранной правильной призмы по заданным координатам положения
базовой точки С ( ХC,YC,ZC ) и параметрам формы: H, Ø D, B. Построение точек А и К,
принадлежащих ребрам призмы.

10.

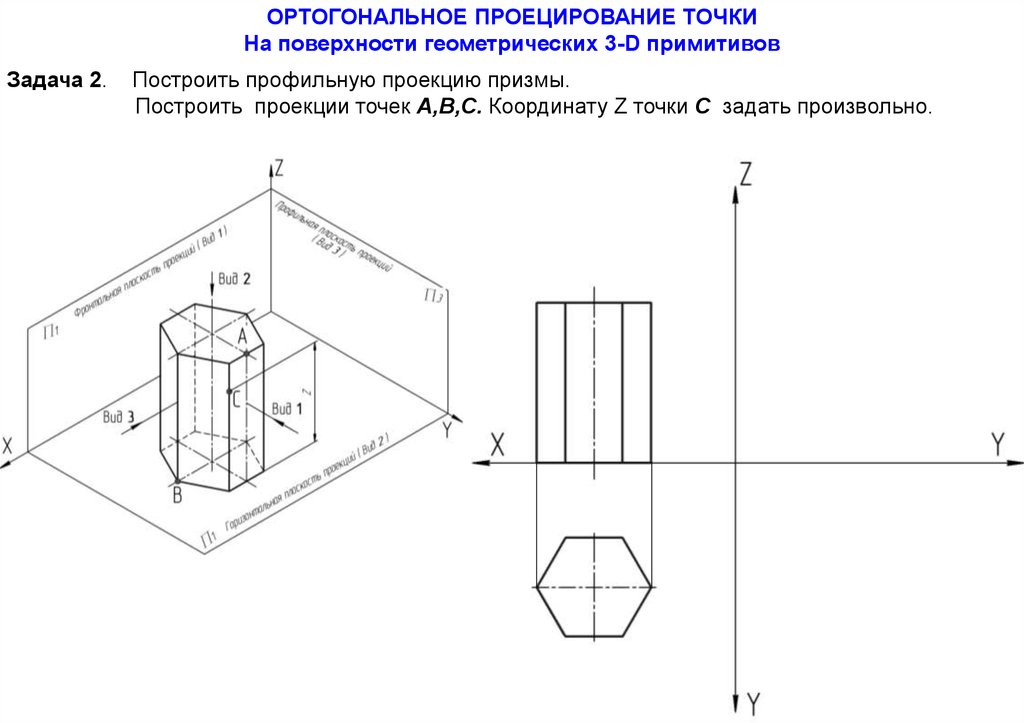
ОРТОГОНАЛЬНОЕ ПРОЕЦИРОВАНИЕ ТОЧКИ
На поверхности геометрических 3-D примитивов
Задача 2.
Построить профильную проекцию призмы.
Построить проекции точек А,В,С. Координату Z точки С задать произвольно.

11.

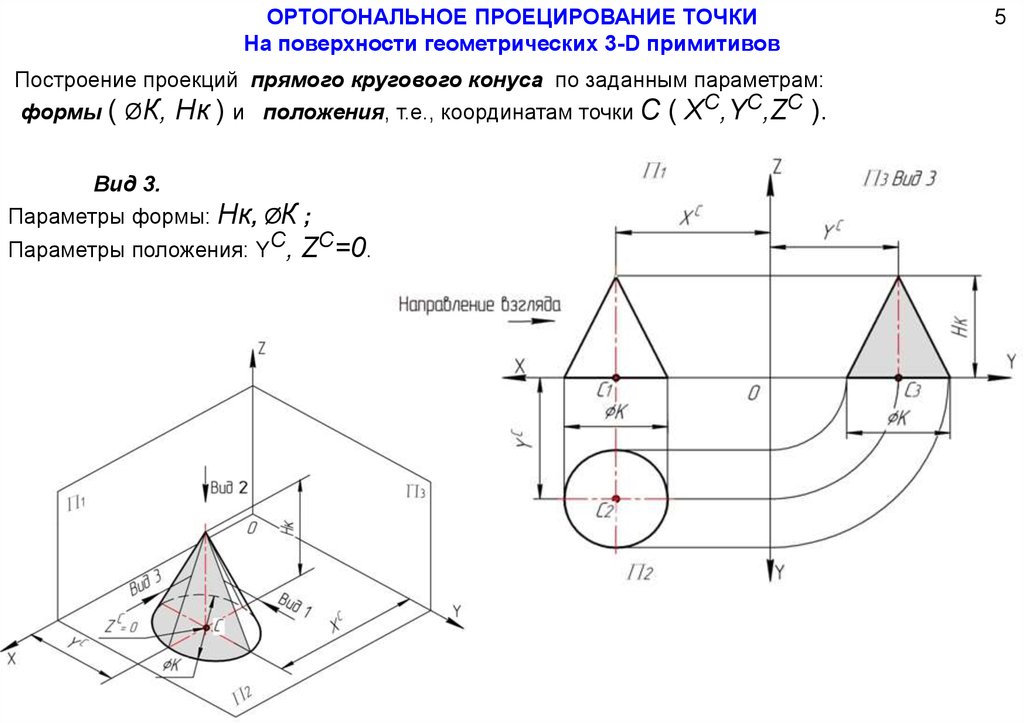
ОРТОГОНАЛЬНОЕ ПРОЕЦИРОВАНИЕ ТОЧКИ
На поверхности геометрических 3-D примитивов
Построение проекций прямого кругового конуса по заданным параметрам:
формы ( ØК, Нк ) и положения, т.е., координатам точки С ( ХC,YC,ZC ).
Вид 3.
Параметры формы: Нк, ØК ;
Параметры положения: YC, ZC=0.
5

12.

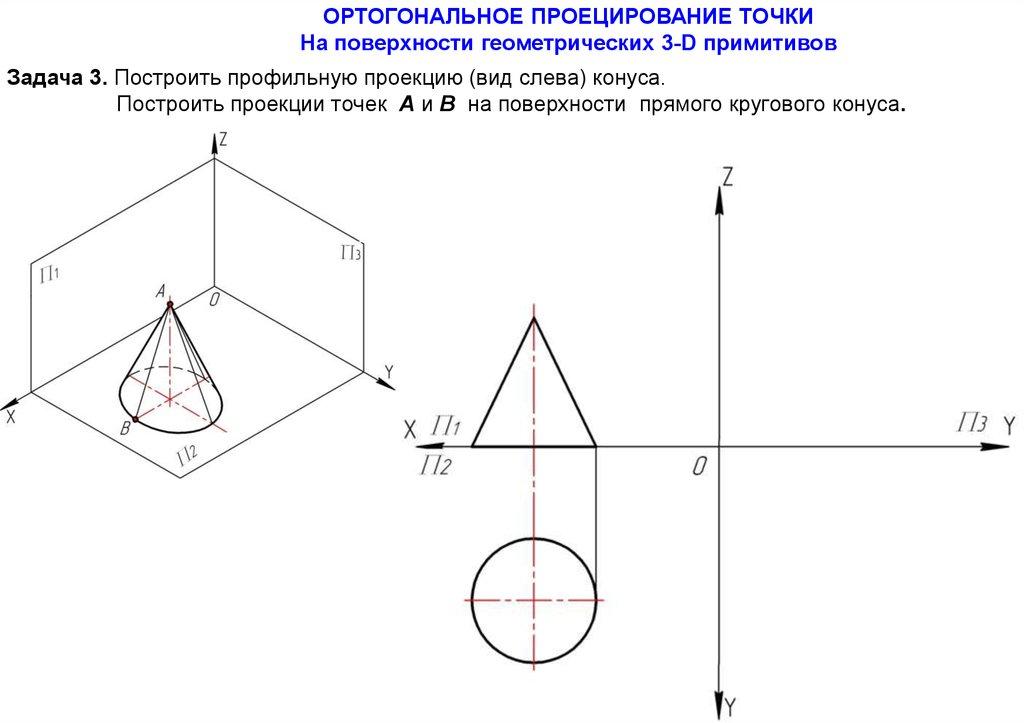
ОРТОГОНАЛЬНОЕ ПРОЕЦИРОВАНИЕ ТОЧКИ
На поверхности геометрических 3-D примитивов
Задача 3. Построить профильную проекцию (вид слева) конуса.
Построить проекции точек А и В на поверхности прямого кругового конуса.

13.

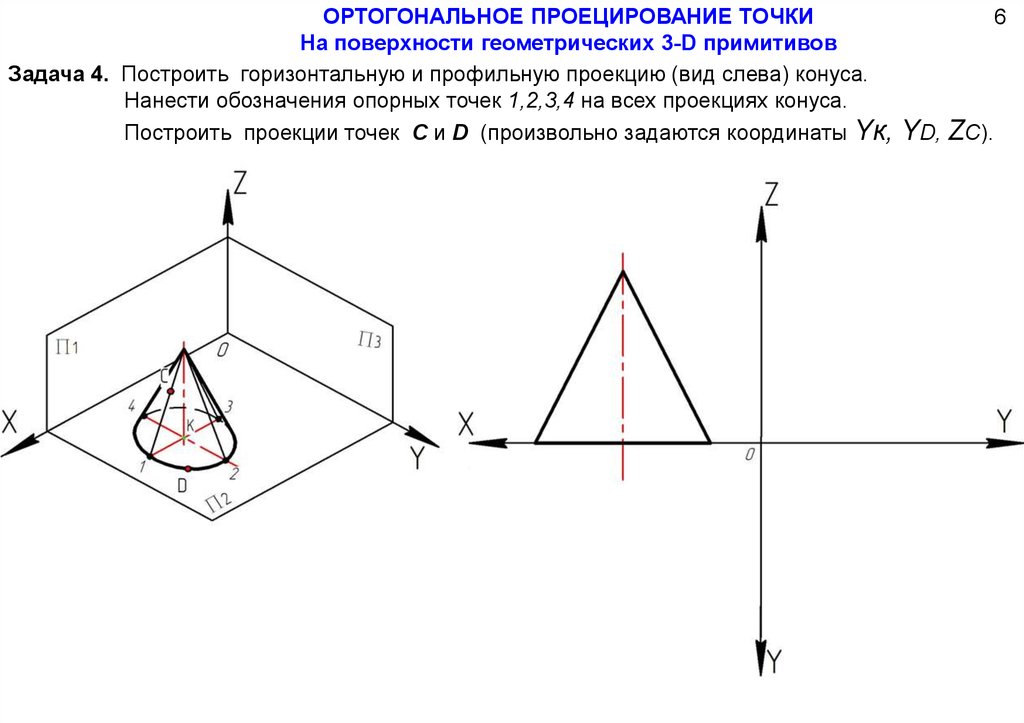
ОРТОГОНАЛЬНОЕ ПРОЕЦИРОВАНИЕ ТОЧКИ
На поверхности геометрических 3-D примитивов
Задача 4. Построить горизонтальную и профильную проекцию (вид слева) конуса.
Нанести обозначения опорных точек 1,2,3,4 на всех проекциях конуса.
Построить проекции точек С и D (произвольно задаются координаты Yк,
6
YD, ZC).

14.

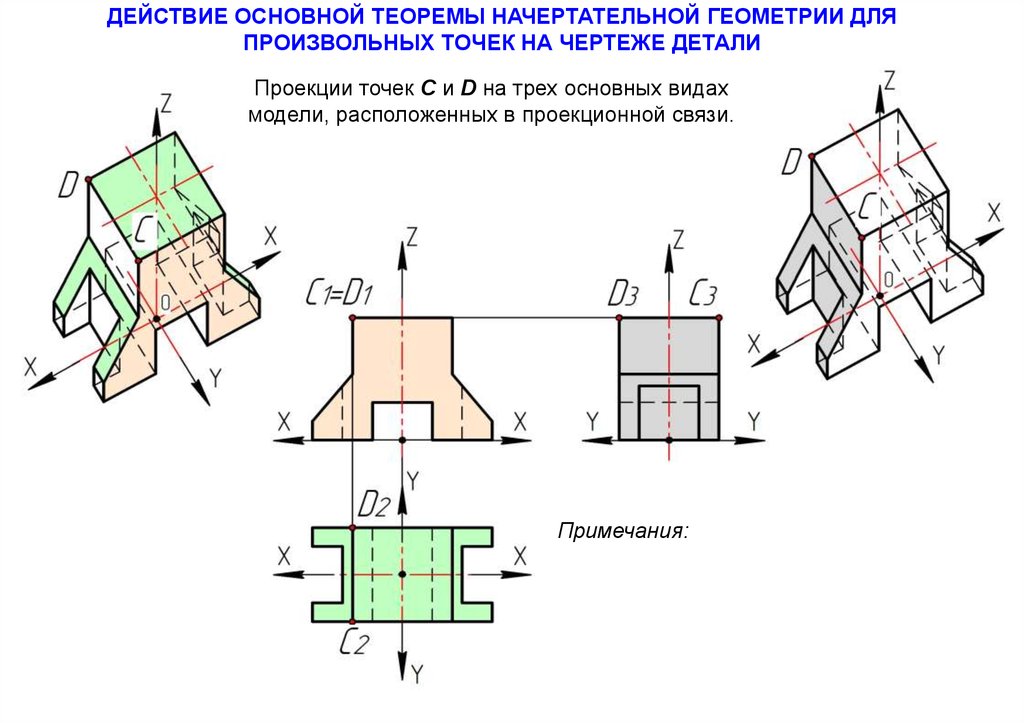
ДЕЙСТВИЕ ОСНОВНОЙ ТЕОРЕМЫ НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ ДЛЯ
ПРОИЗВОЛЬНЫХ ТОЧЕК НА ЧЕРТЕЖЕ ДЕТАЛИ
Проекции точек С и D на трех основных видах
модели, расположенных в проекционной связи.
Примечания:

15.

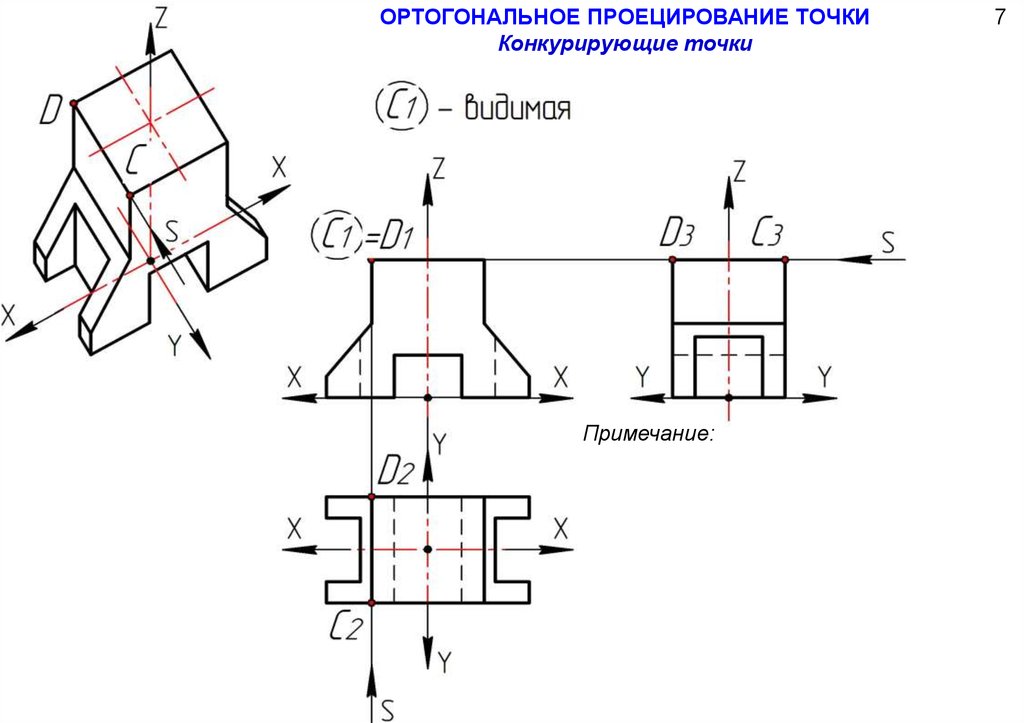
ОРТОГОНАЛЬНОЕ ПРОЕЦИРОВАНИЕ ТОЧКИ
Конкурирующие точки
Примечание:
7

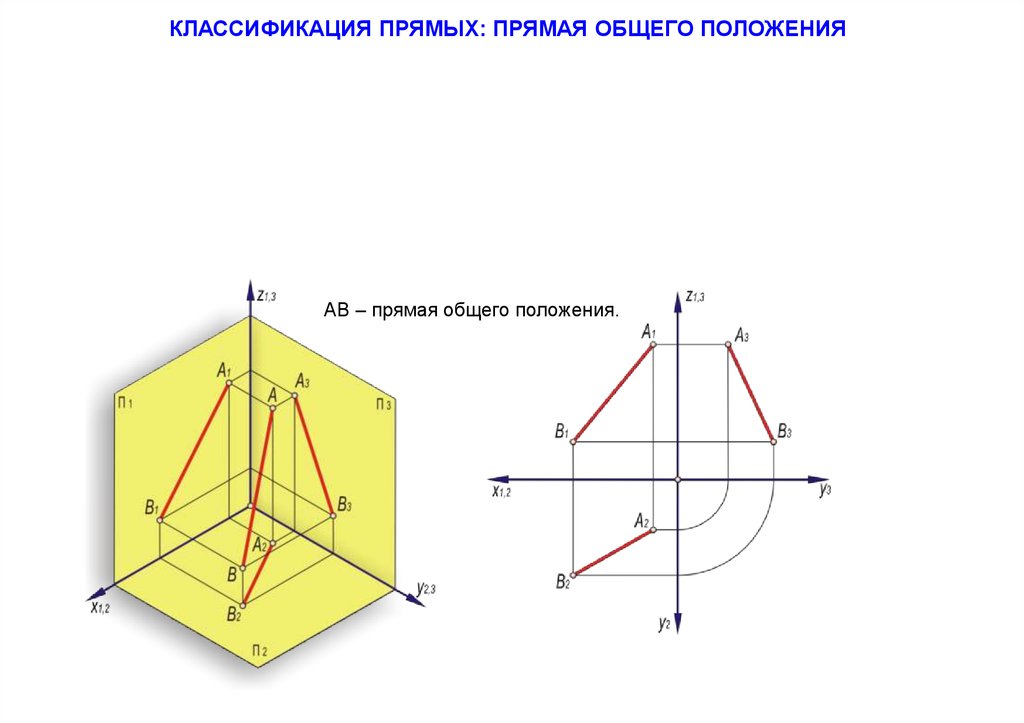
16.

КЛАССИФИКАЦИЯ ПРЯМЫХ: ПРЯМАЯ ОБЩЕГО ПОЛОЖЕНИЯ
АВ – прямая общего положения.

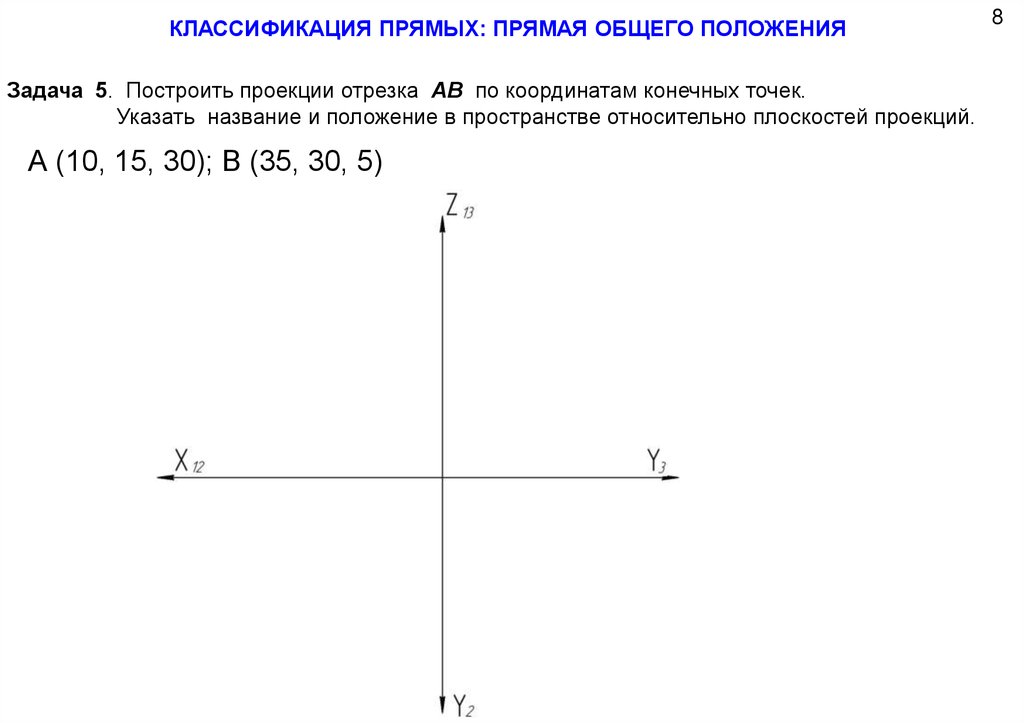
17.

КЛАССИФИКАЦИЯ ПРЯМЫХ: ПРЯМАЯ ОБЩЕГО ПОЛОЖЕНИЯ
Задача 5. Построить проекции отрезка АВ по координатам конечных точек.
Указать название и положение в пространстве относительно плоскостей проекций.
А (10, 15, 30); В (35, 30, 5)
8

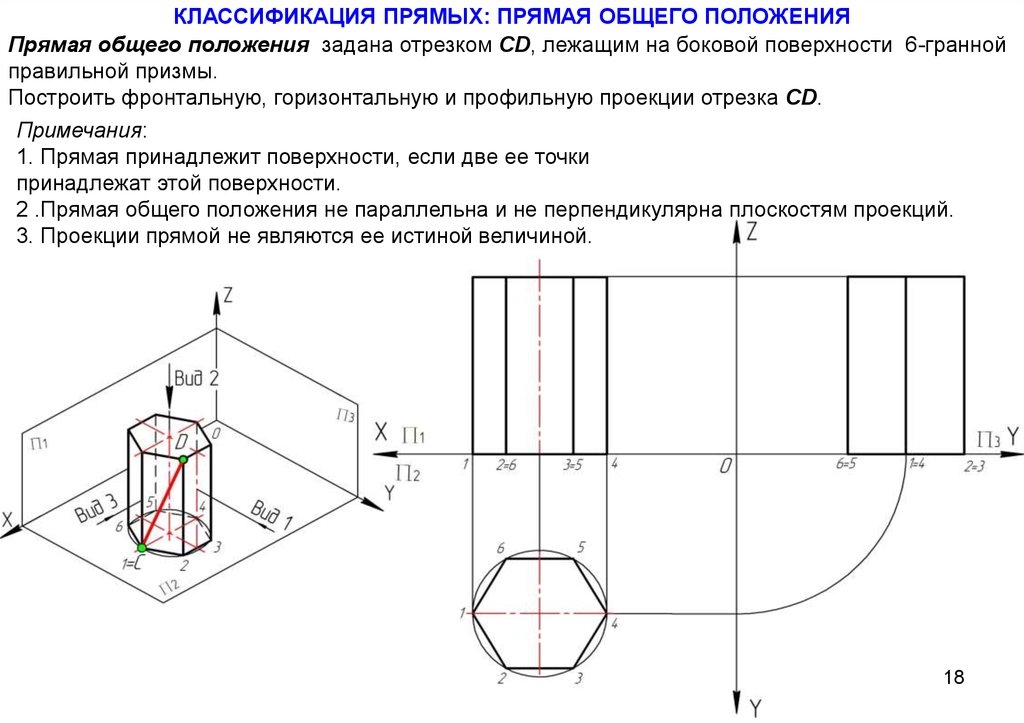
18.

КЛАССИФИКАЦИЯ ПРЯМЫХ: ПРЯМАЯ ОБЩЕГО ПОЛОЖЕНИЯ
Прямая общего положения задана отрезком СD, лежащим на боковой поверхности 6-гранной
правильной призмы.
Построить фронтальную, горизонтальную и профильную проекции отрезка СD.
Примечания:
1. Прямая принадлежит поверхности, если две ее точки
принадлежат этой поверхности.
2 .Прямая общего положения не параллельна и не перпендикулярна плоскостям проекций.
3. Проекции прямой не являются ее истиной величиной.
18

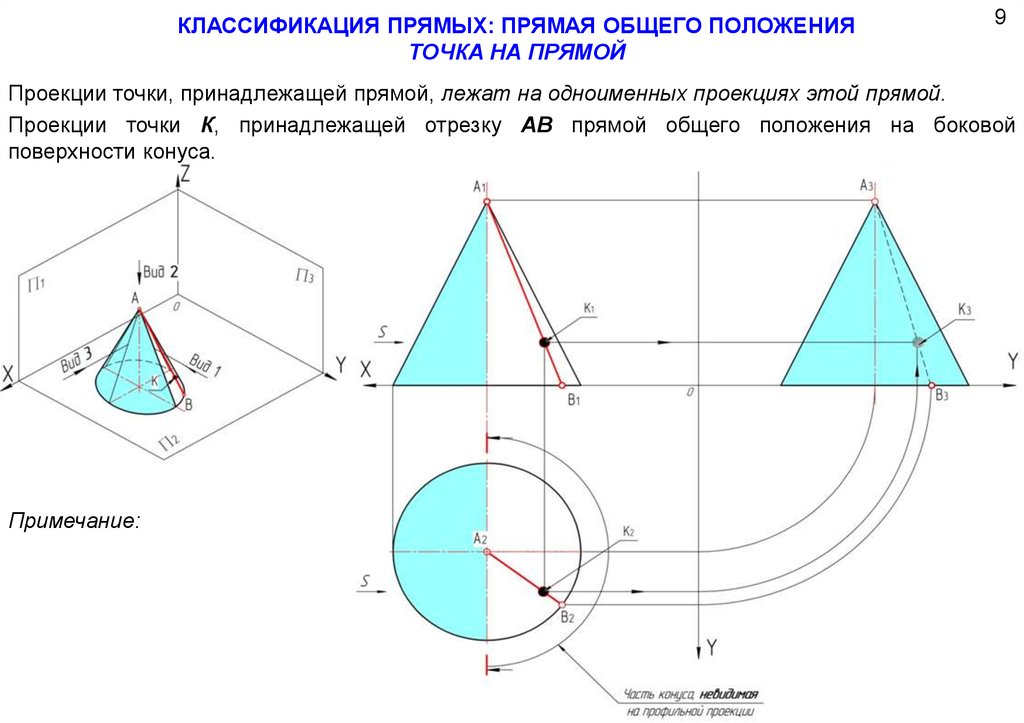
19.

КЛАССИФИКАЦИЯ ПРЯМЫХ: ПРЯМАЯ ОБЩЕГО ПОЛОЖЕНИЯ
ТОЧКА НА ПРЯМОЙ
9
Проекции точки, принадлежащей прямой, лежат на одноименных проекциях этой прямой.
Проекции точки К, принадлежащей отрезку АВ прямой общего положения на боковой
поверхности конуса.
Примечание:

20.

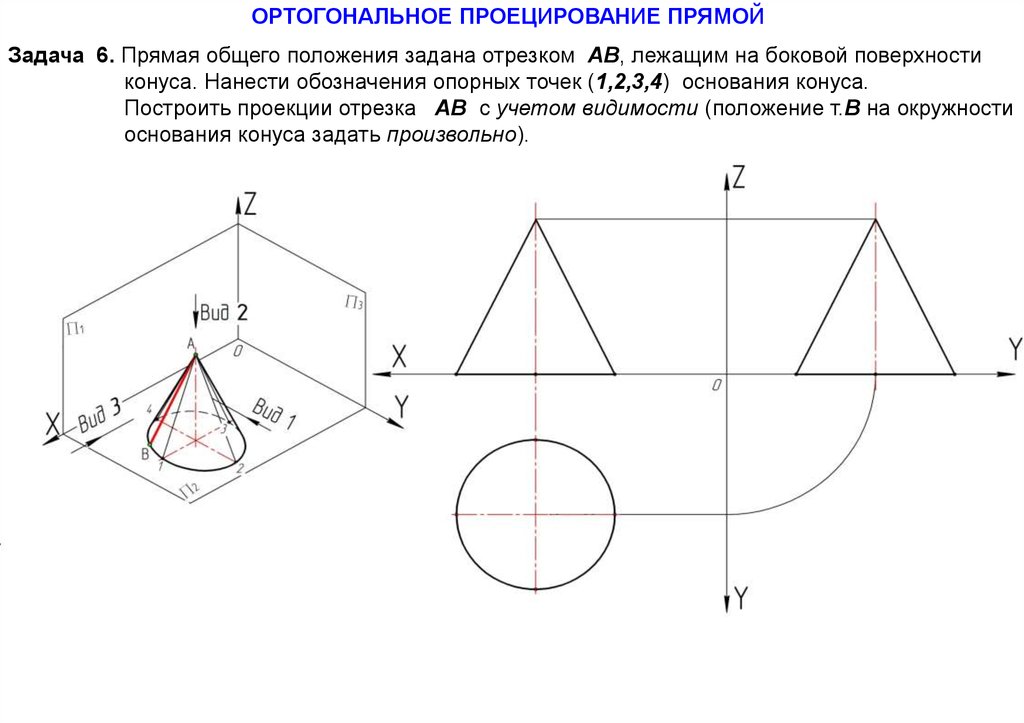
ОРТОГОНАЛЬНОЕ ПРОЕЦИРОВАНИЕ ПРЯМОЙ
Задача 6. Прямая общего положения задана отрезком АВ, лежащим на боковой поверхности
конуса. Нанести обозначения опорных точек (1,2,3,4) основания конуса.
Построить проекции отрезка АВ с учетом видимости (положение т.В на окружности
основания конуса задать произвольно).

21.

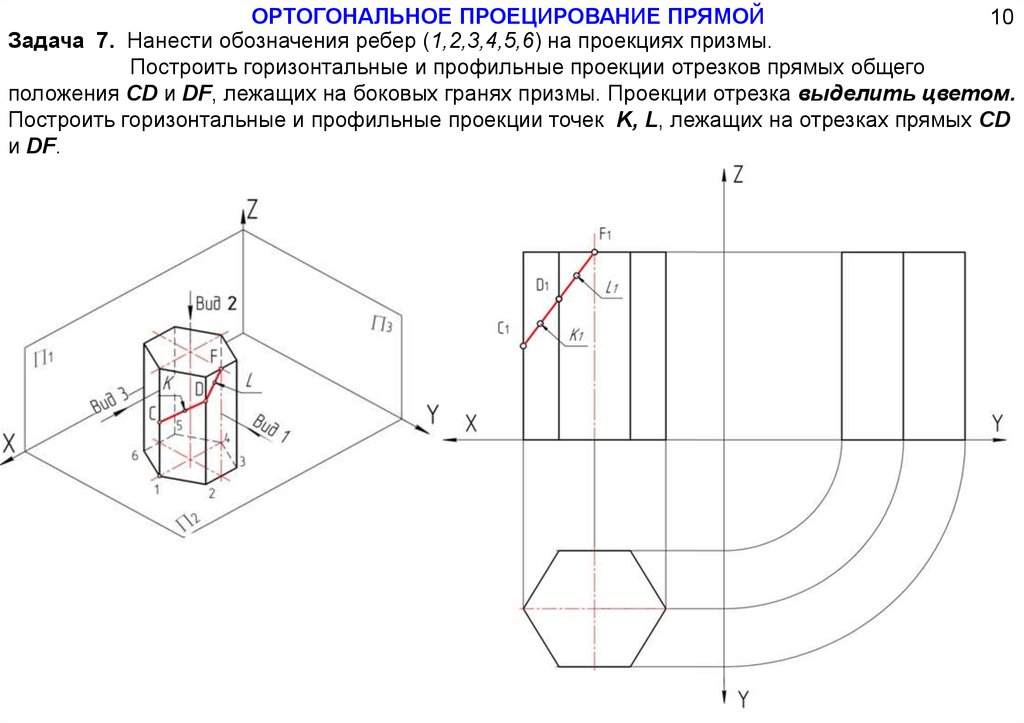
ОРТОГОНАЛЬНОЕ ПРОЕЦИРОВАНИЕ ПРЯМОЙ
10
Задача 7. Нанести обозначения ребер (1,2,3,4,5,6) на проекциях призмы.
Построить горизонтальные и профильные проекции отрезков прямых общего
положения CD и DF, лежащих на боковых гранях призмы. Проекции отрезка выделить цветом.
Построить горизонтальные и профильные проекции точек K, L, лежащих на отрезках прямых CD
и DF.

22.

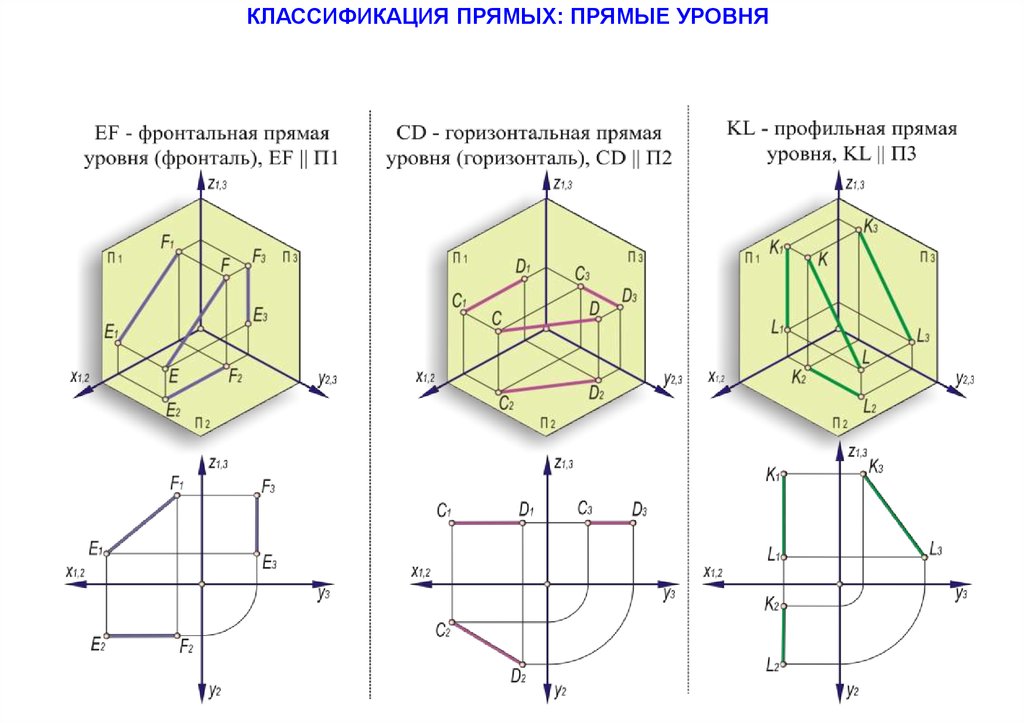
КЛАССИФИКАЦИЯ ПРЯМЫХ: ПРЯМЫЕ УРОВНЯ

23.

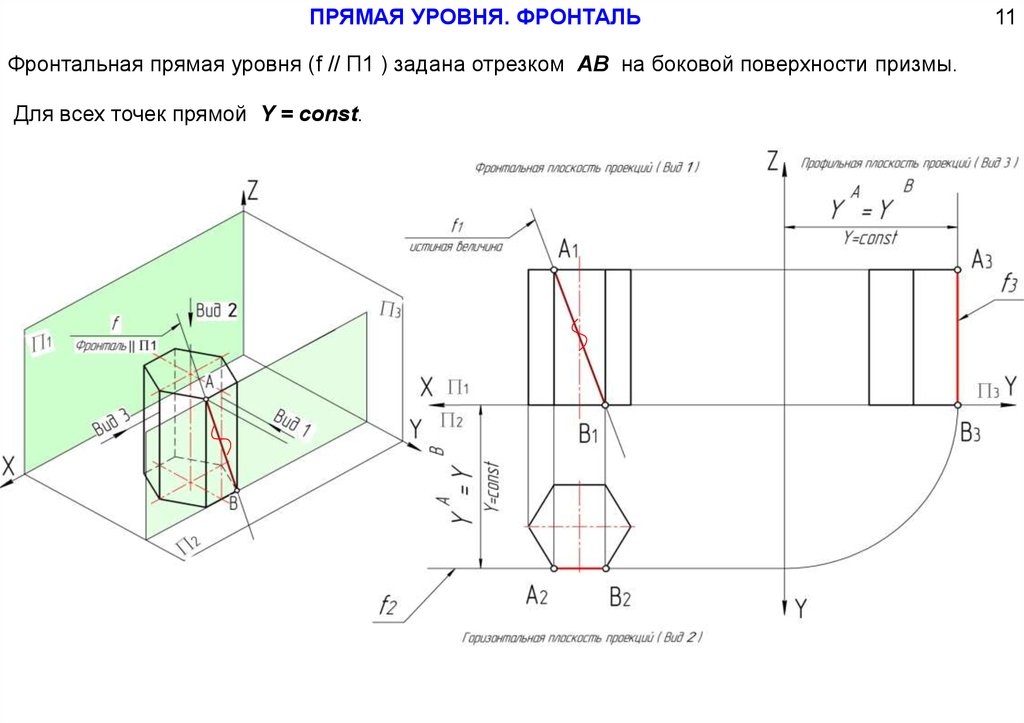
ПРЯМАЯ УРОВНЯ. ФРОНТАЛЬ
Фронтальная прямая уровня (f // П1 ) задана отрезком АВ на боковой поверхности призмы.
Для всех точек прямой Y = const.
11

24.

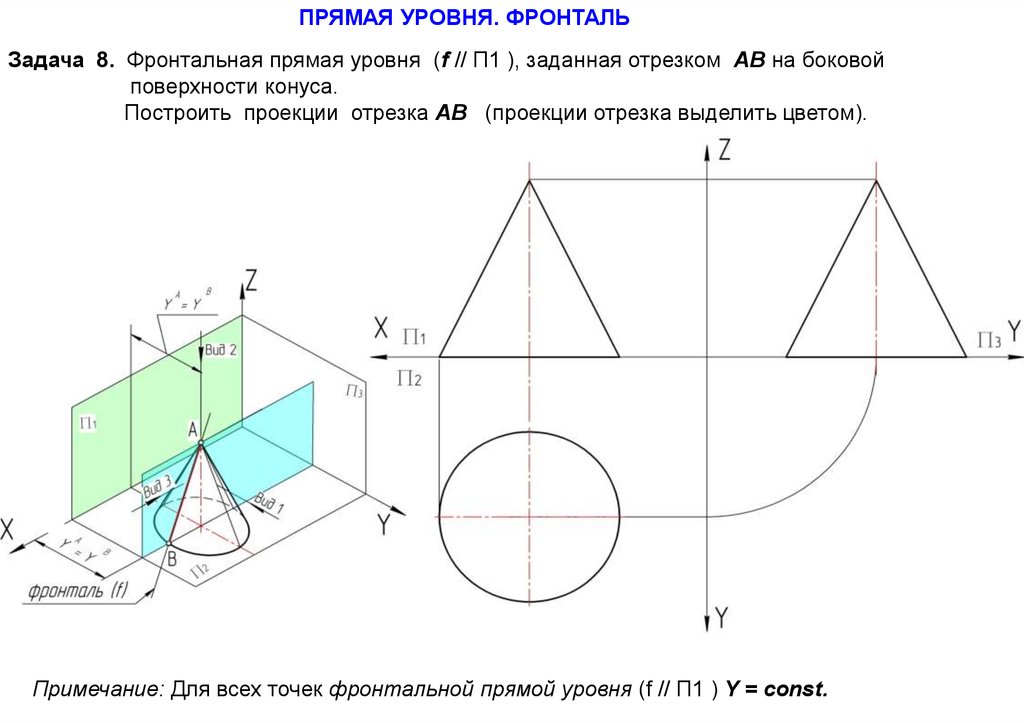
ПРЯМАЯ УРОВНЯ. ФРОНТАЛЬ
Задача 8. Фронтальная прямая уровня (f // П1 ), заданная отрезком АВ на боковой
поверхности конуса.
Построить проекции отрезка АВ (проекции отрезка выделить цветом).
Примечание: Для всех точек фронтальной прямой уровня (f // П1 ) Y = const.

25.

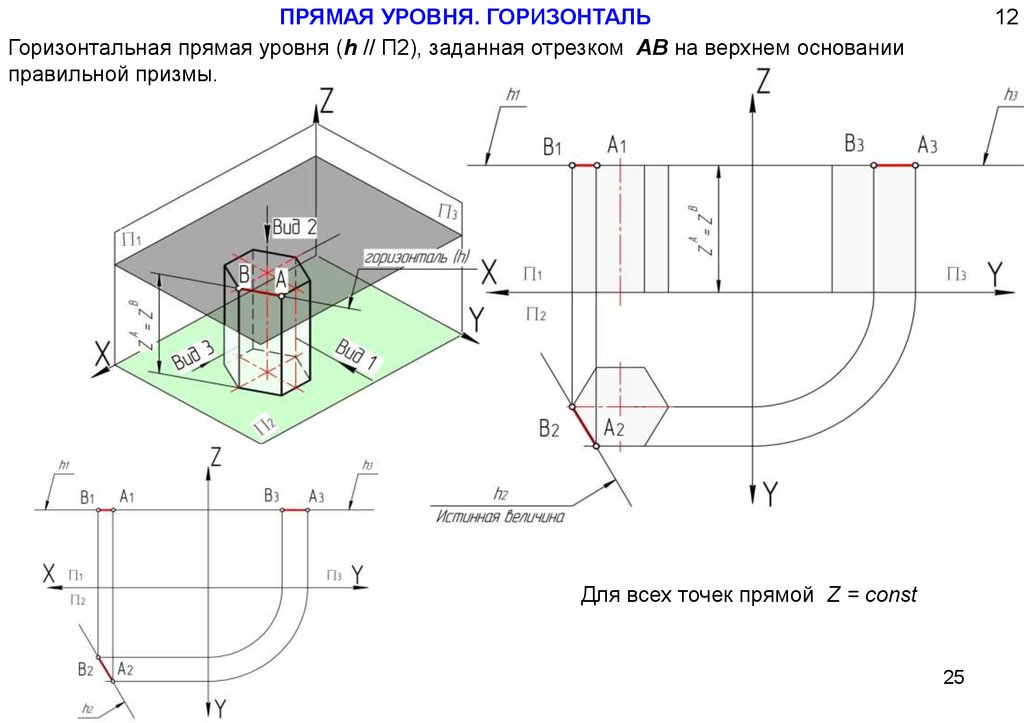
ПРЯМАЯ УРОВНЯ. ГОРИЗОНТАЛЬ
Горизонтальная прямая уровня (h // П2), заданная отрезком АВ на верхнем основании
правильной призмы.
12
Для всех точек прямой Z = const
25

26.

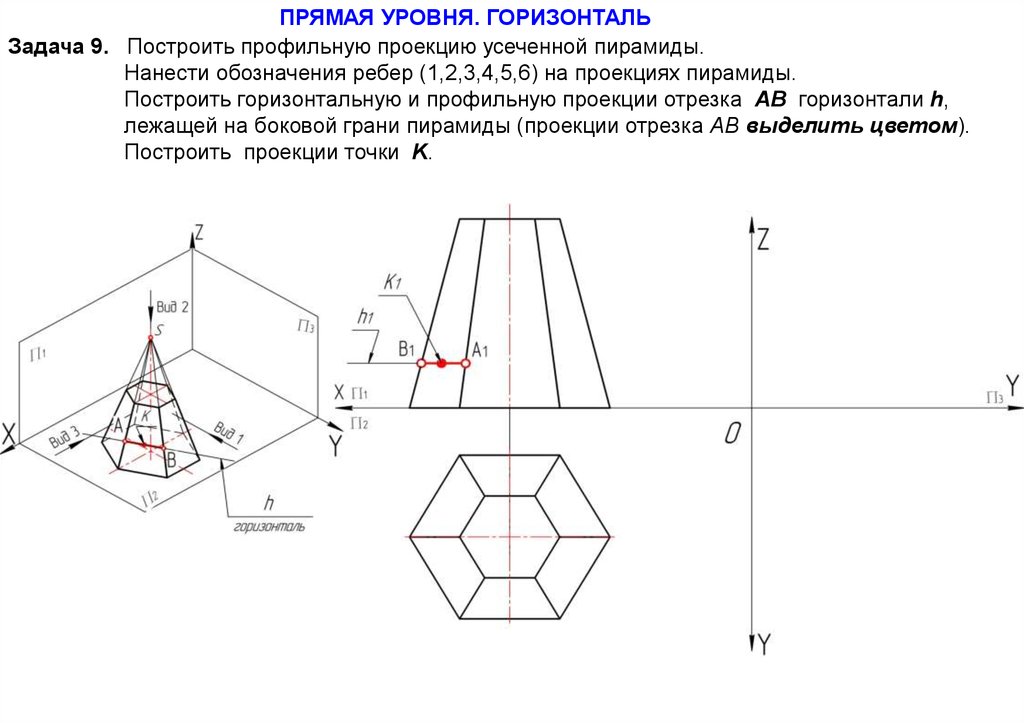
ПРЯМАЯ УРОВНЯ. ГОРИЗОНТАЛЬ
Задача 9. Построить профильную проекцию усеченной пирамиды.
Нанести обозначения ребер (1,2,3,4,5,6) на проекциях пирамиды.
Построить горизонтальную и профильную проекции отрезка АВ горизонтали h,
лежащей на боковой грани пирамиды (проекции отрезка АВ выделить цветом).
Построить проекции точки K.
Точка на горизонтальной прямой уровня (h), заданной отрезком (АВ),
принадлежащим боковой поверхности усеченной пирамиды.

27.

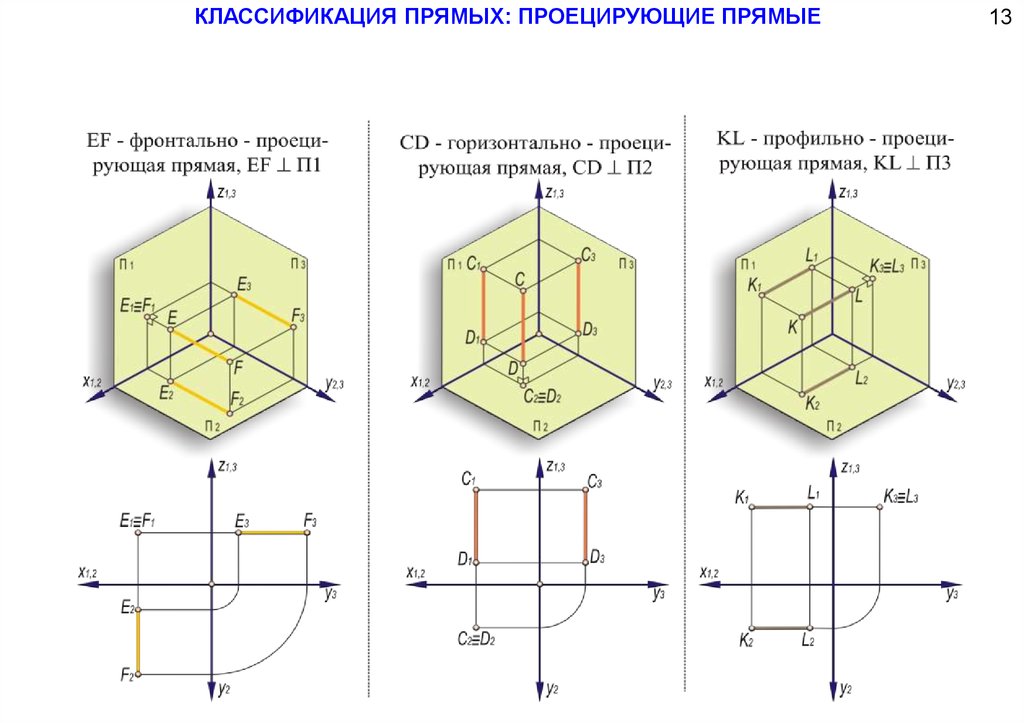
КЛАССИФИКАЦИЯ ПРЯМЫХ: ПРОЕЦИРУЮЩИЕ ПРЯМЫЕ
13

28.

КЛАССИФИКАЦИЯ ПРЯМЫХ. ПРОЕЦИРУЮЩИЕ ПРЯМЫЕ
Фронтально-проецирующая прямая задана отрезком АВ на боковой поверхности прямого
кругового цилиндра.
Примечания:

29.

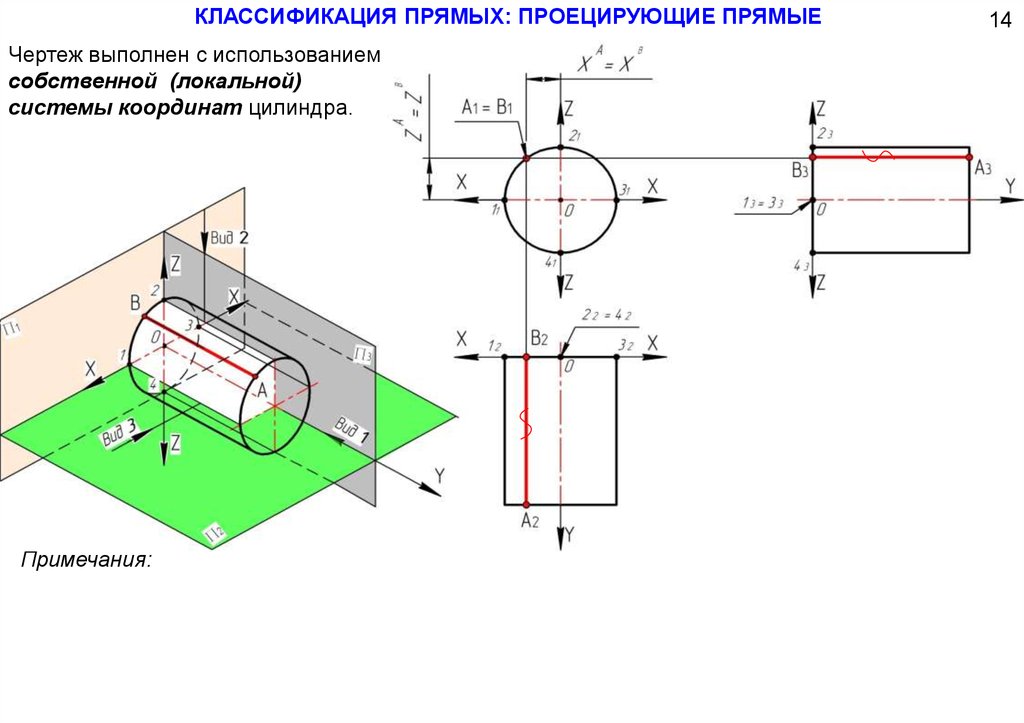
КЛАССИФИКАЦИЯ ПРЯМЫХ: ПРОЕЦИРУЮЩИЕ ПРЯМЫЕ
14
Чертеж выполнен с использованием
Фронтально-проецирующая
собственной (локальной)
прямая задана отрезком (АВ)
системы координат цилиндра.
на боковой поверхности прямого
кругового цилиндра.
Чертеж выполнен
с использованием
собственной (локальной)
системы координат пирамиды.
Примечания:

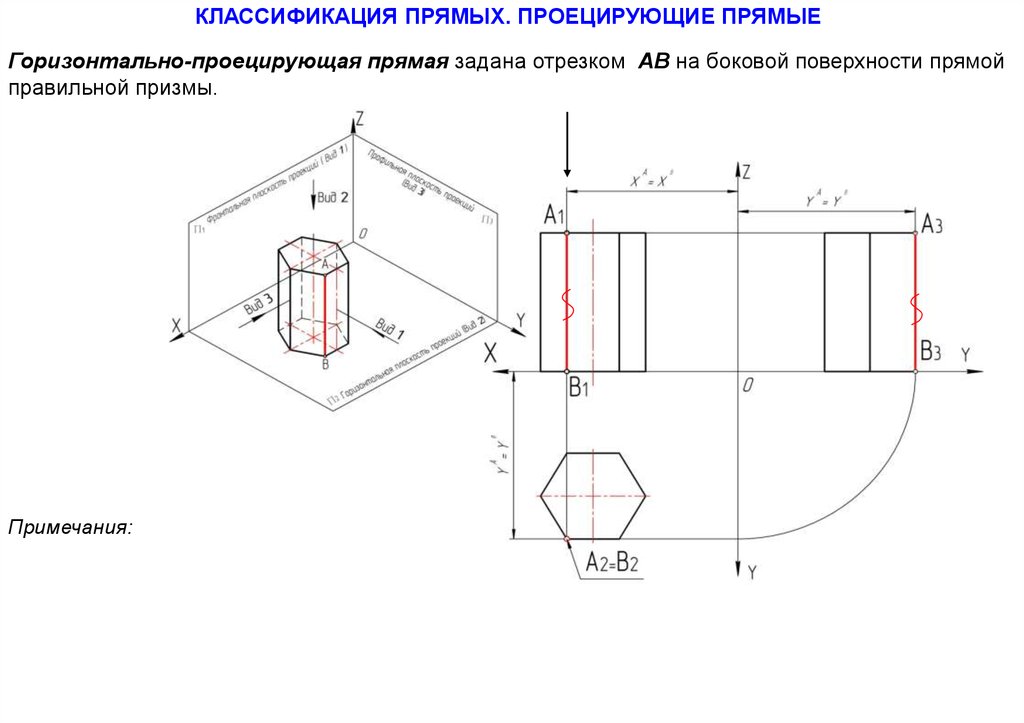
30.

КЛАССИФИКАЦИЯ ПРЯМЫХ. ПРОЕЦИРУЮЩИЕ ПРЯМЫЕ
Горизонтально-проецирующая прямая задана отрезком АВ на боковой поверхности прямой
правильной призмы.
Примечания:

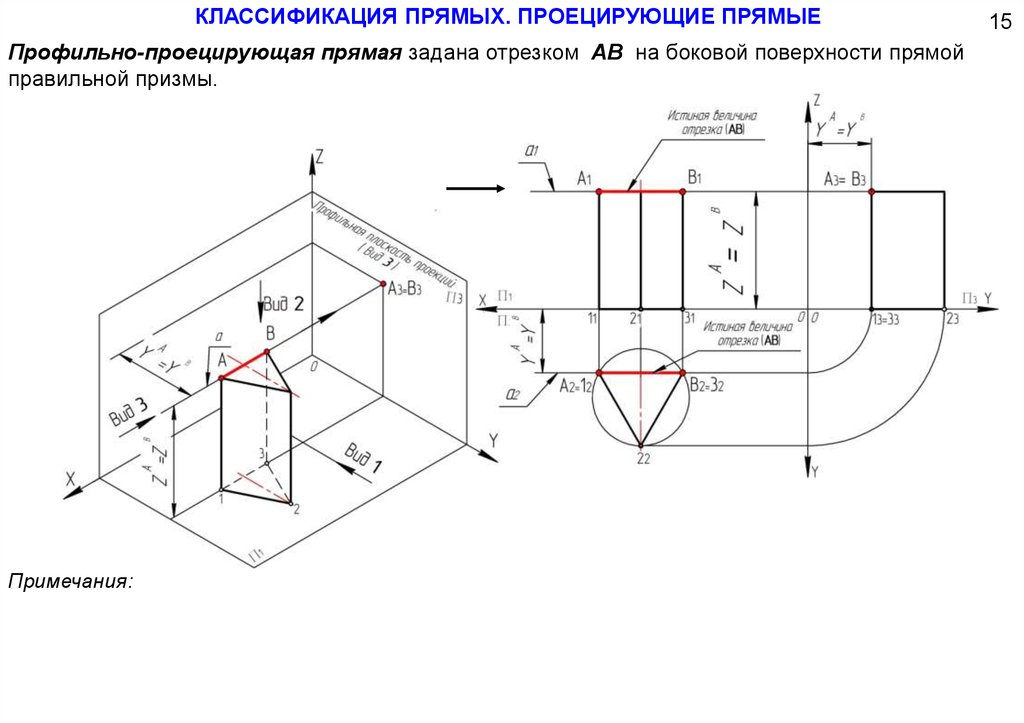
31.

КЛАССИФИКАЦИЯ ПРЯМЫХ. ПРОЕЦИРУЮЩИЕ ПРЯМЫЕ
Профильно-проецирующая прямая задана отрезком АВ на боковой поверхности прямой
правильной призмы.
Примечания:
15

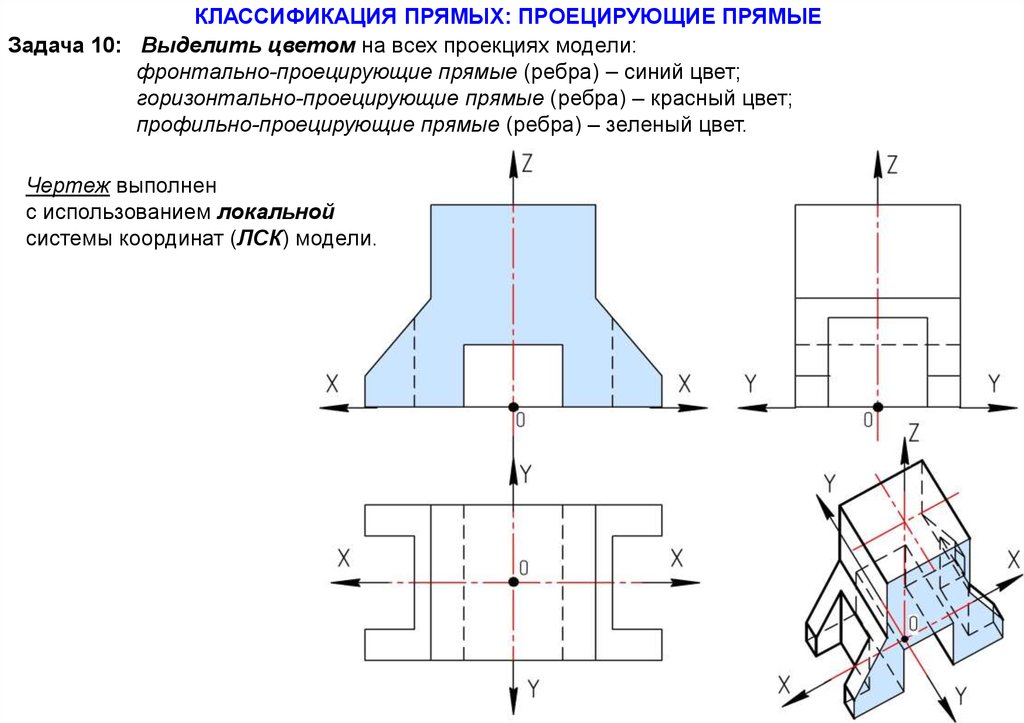
32.

КЛАССИФИКАЦИЯ ПРЯМЫХ: ПРОЕЦИРУЮЩИЕ ПРЯМЫЕ
Задача 10: Выделить цветом на всех проекциях модели:
фронтально-проецирующие прямые (ребра) – синий цвет;
горизонтально-проецирующие прямые (ребра) – красный цвет;
профильно-проецирующие прямые (ребра) – зеленый цвет.
Чертеж выполнен
с использованием локальной
системы координат (ЛСК) модели.

33.

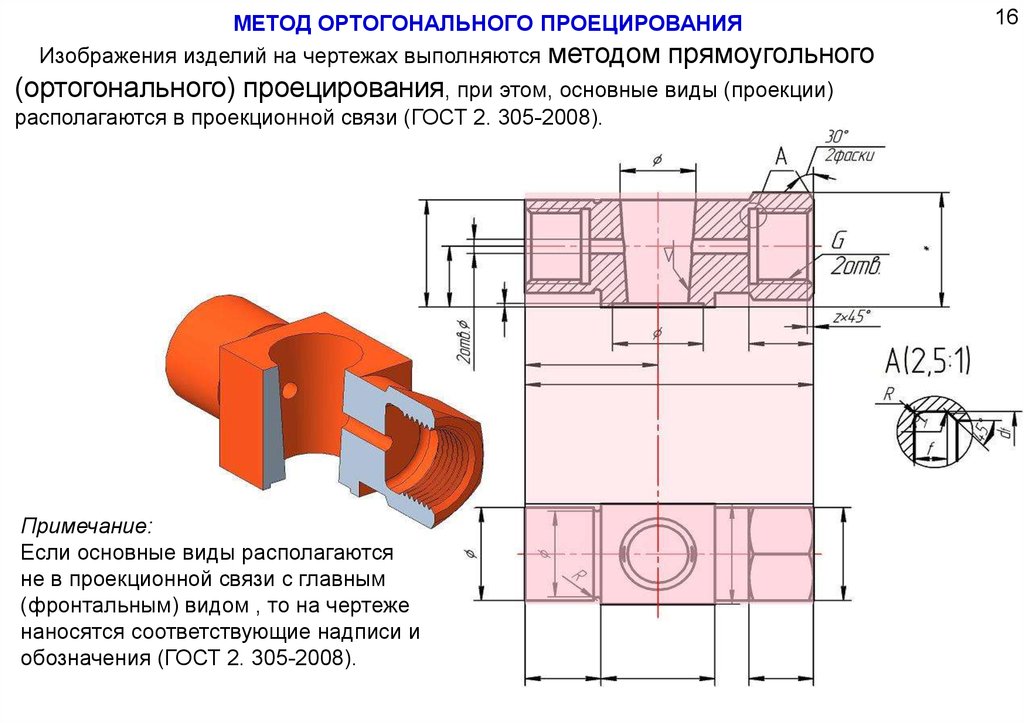
МЕТОД ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ
Изображения изделий на чертежах выполняются методом прямоугольного
(ортогонального) проецирования, при этом, основные виды (проекции)
располагаются в проекционной связи (ГОСТ 2. 305-2008).
Примечание:
Если основные виды располагаются
не в проекционной связи с главным
(фронтальным) видом , то на чертеже
наносятся соответствующие надписи и
обозначения (ГОСТ 2. 305-2008).
16

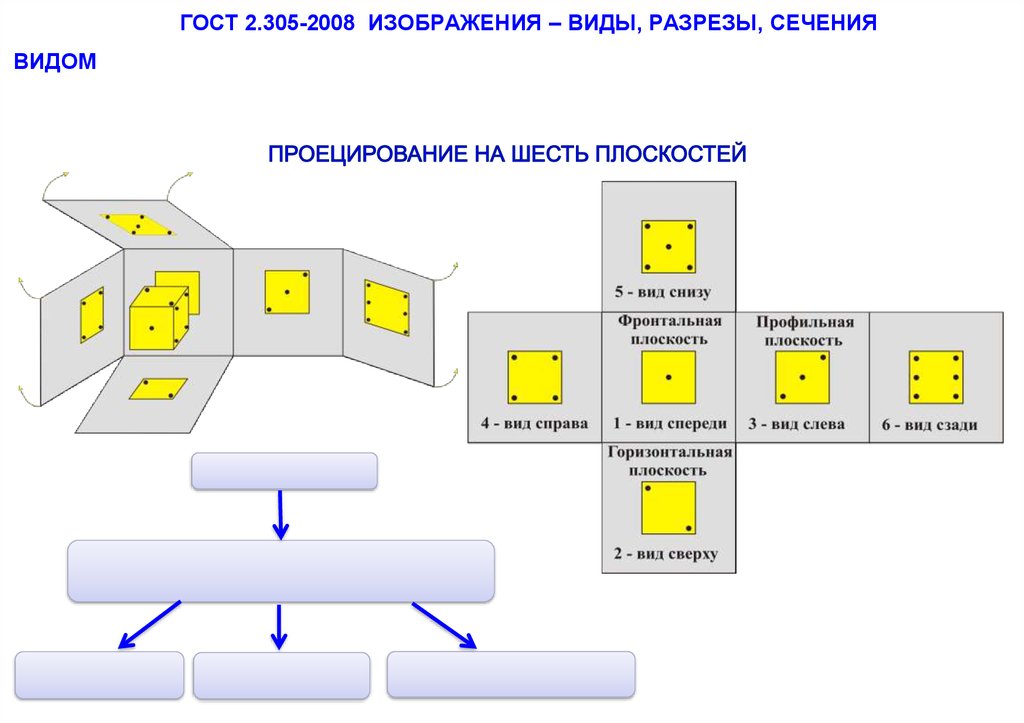
34. ГОСТ 2.305-2008 ИЗОБРАЖЕНИЯ – ВИДЫ, РАЗРЕЗЫ, СЕЧЕНИЯ

ВИДОМ

35.

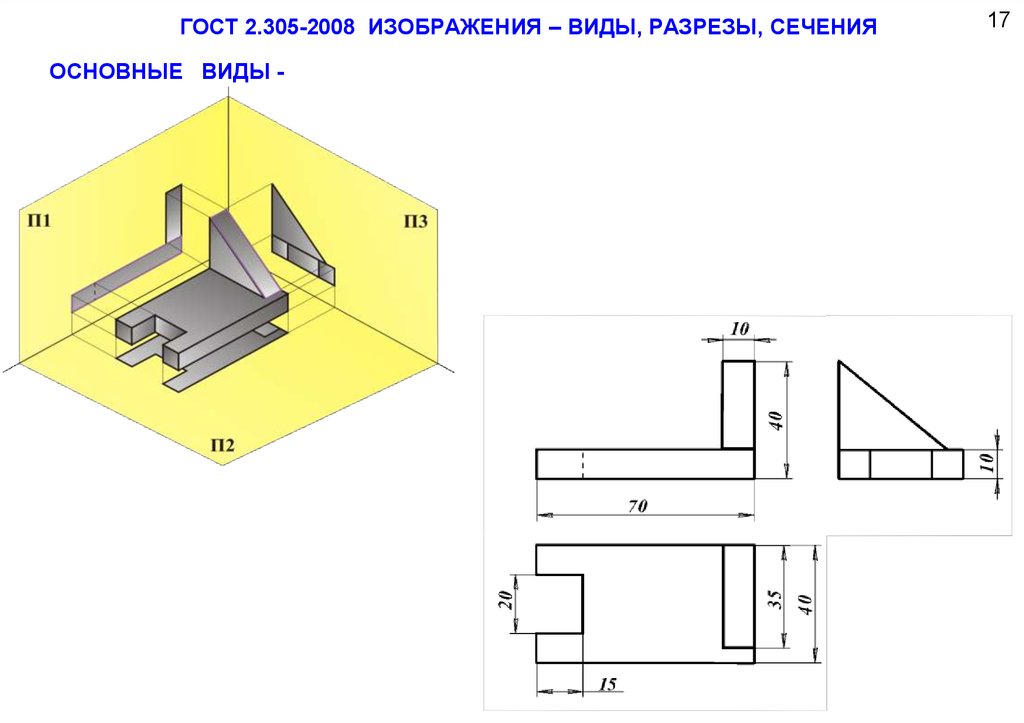
ГОСТ 2.305-2008 ИЗОБРАЖЕНИЯ – ВИДЫ, РАЗРЕЗЫ, СЕЧЕНИЯ
ОСНОВНЫЕ ВИДЫ -
17

36.

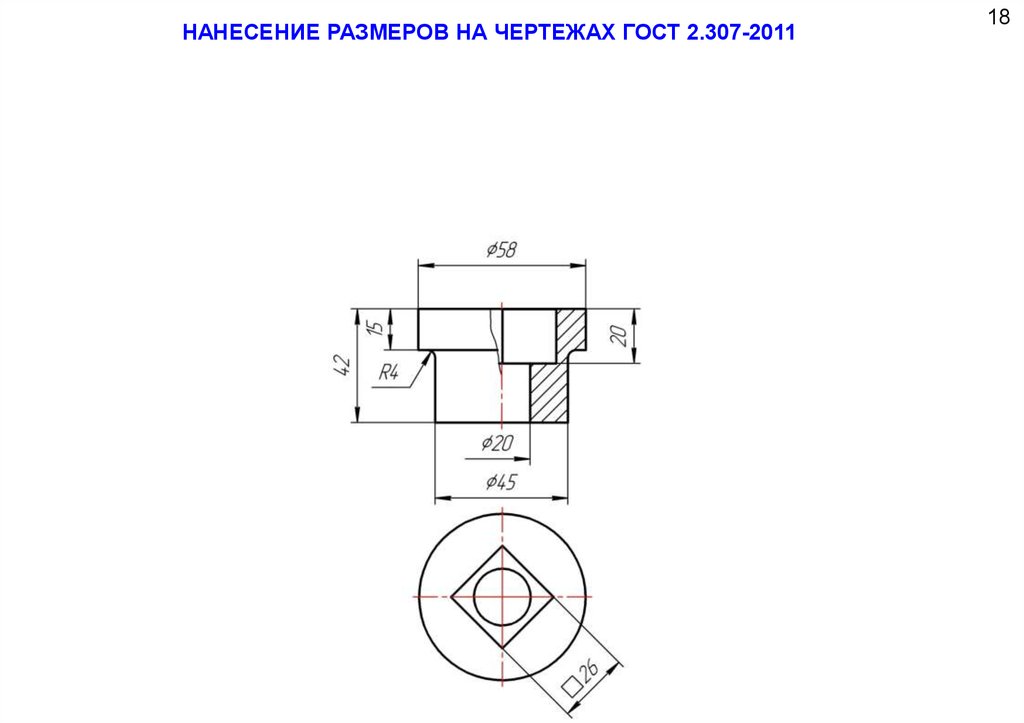
ГОСТ 2.307 - 2011 (взамен 2.307-68)
НАНЕСЕНИЕ РАЗМЕРОВ И ПРЕДЕЛЬНЫХ ОТКЛОНЕНИЙ
Настоящий стандарт устанавливает правила нанесения размеров и предельных отклонений в
графических документах на изделия всех отраслей промышленности и строительства.
Представленные на чертеже изображения устанавливают форму предмета, а для определения
величины (длины, ширины, диаметра, высоты и т.д.) изображенного предмета и его элементов
служат размерные числа.

37.

НАНЕСЕНИЕ РАЗМЕРОВ НА ЧЕРТЕЖАХ ГОСТ 2.307-2011
18

38.

ОТНОСИТЕЛЬНОЕ ПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ: ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ

39.

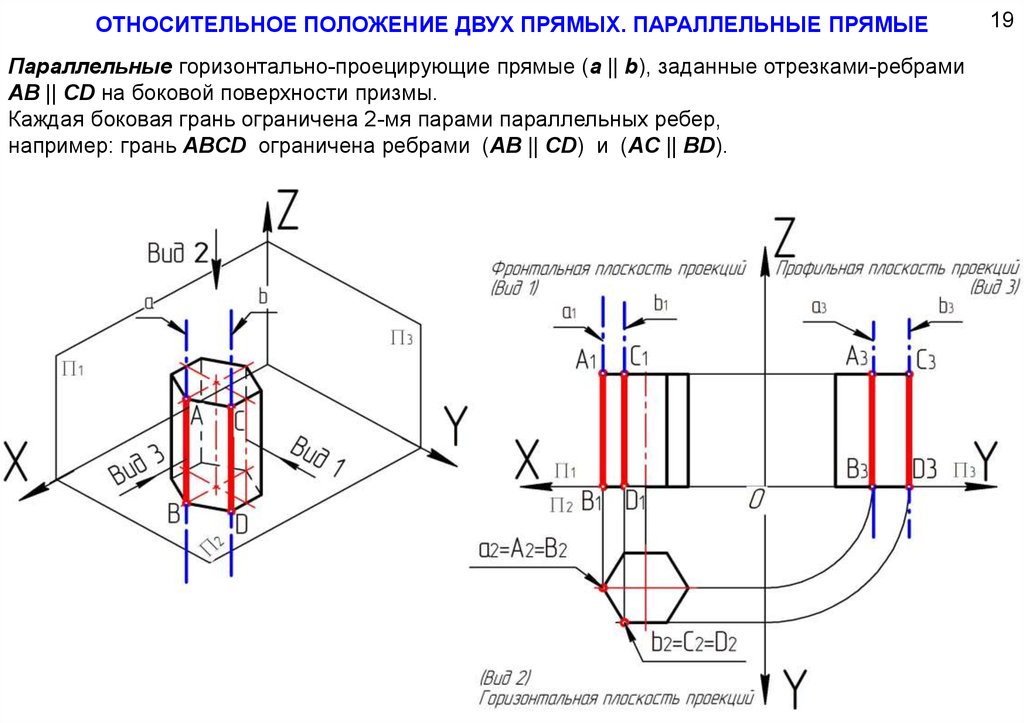
ОТНОСИТЕЛЬНОЕ ПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ. ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ
Параллельные горизонтально-проецирующие прямые (a || b), заданные отрезками-ребрами
AB || CD на боковой поверхности призмы.
Каждая боковая грань ограничена 2-мя парами параллельных ребер,
например: грань ABCD ограничена ребрами (AB || CD) и (AС || ВD).
19

40.

ОТНОСИТЕЛЬНОЕ ПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ. ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ
Параллельные горизонтальные
прямые уровня (h || h'),
заданные отрезками AB || CD

41.

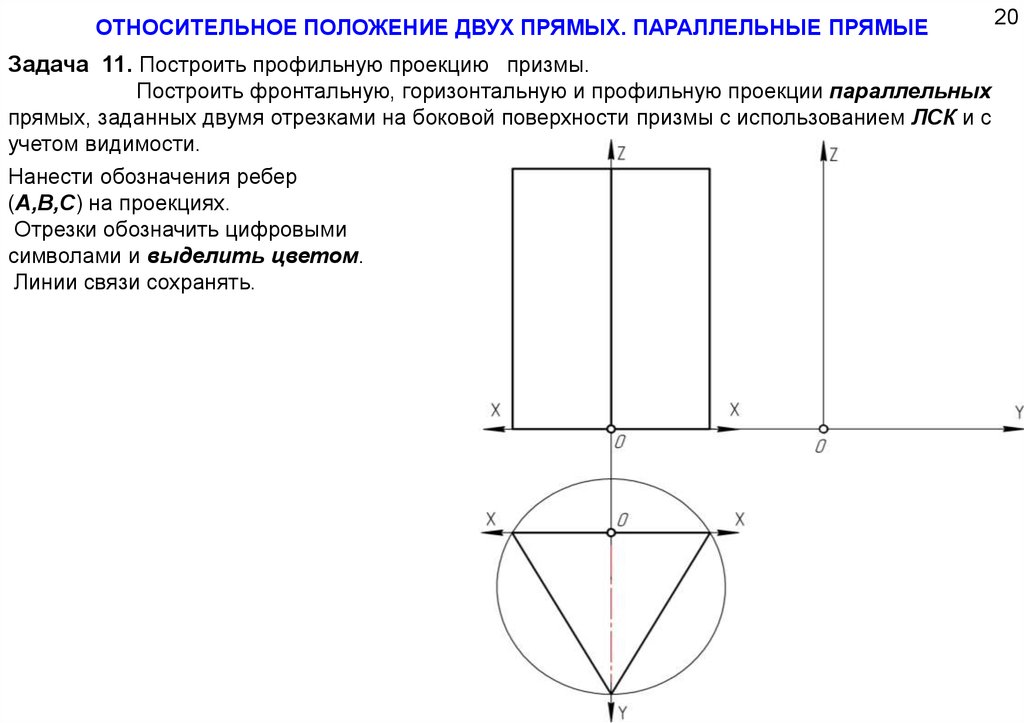
ОТНОСИТЕЛЬНОЕ ПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ. ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ
Задача 11. Построить профильную проекцию призмы.
Построить фронтальную, горизонтальную и профильную проекции параллельных
прямых, заданных двумя отрезками на боковой поверхности призмы с использованием ЛСК и с
учетом видимости.
Нанести обозначения ребер
(А,В,С) на проекциях.
Отрезки обозначить цифровыми
символами и выделить цветом.
Линии связи сохранять.
20

42.

ОТНОСИТЕЛЬНОЕ ПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ: ПЕРЕСЕКАЮЩИЕСЯ ПРЯМЫЕ

43.

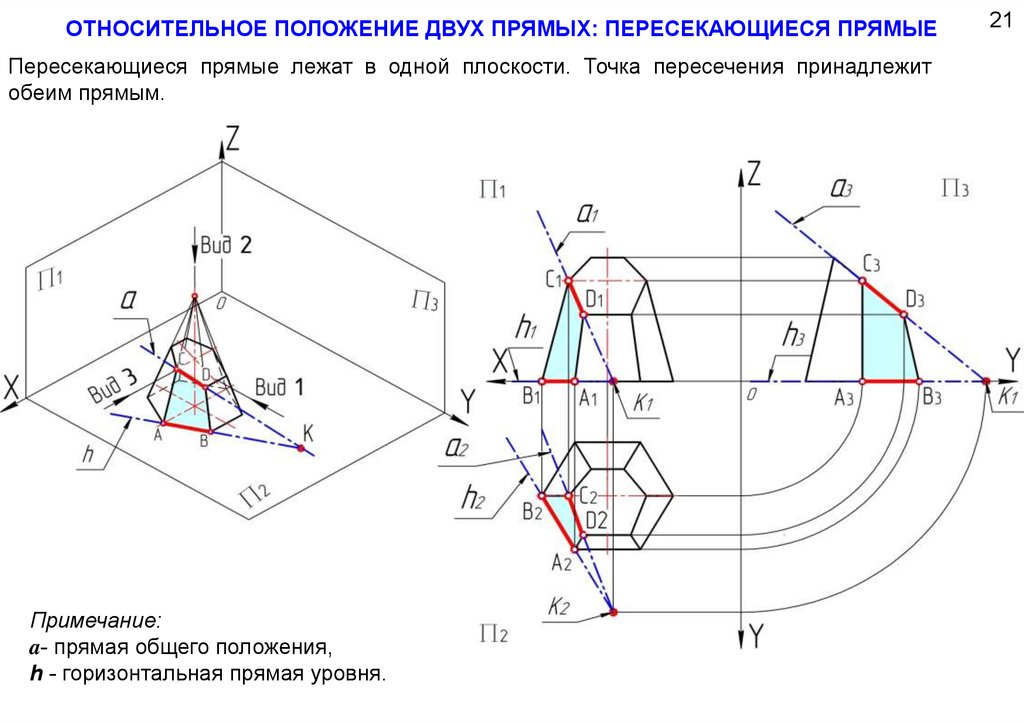
ОТНОСИТЕЛЬНОЕ ПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ: ПЕРЕСЕКАЮЩИЕСЯ ПРЯМЫЕ
Пересекающиеся прямые лежат в одной плоскости. Точка пересечения принадлежит
обеим прямым.
Примечание:
a- прямая общего положения,
h - горизонтальная прямая уровня.
21

44.

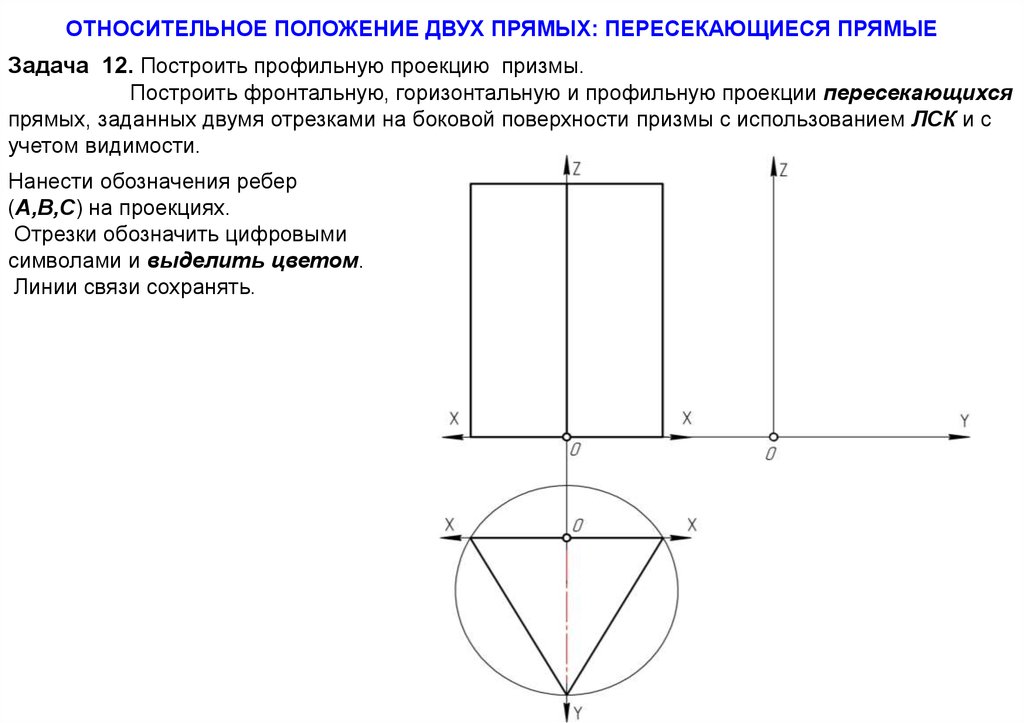
ОТНОСИТЕЛЬНОЕ ПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ: ПЕРЕСЕКАЮЩИЕСЯ ПРЯМЫЕ
Задача 12. Построить профильную проекцию призмы.
Построить фронтальную, горизонтальную и профильную проекции пересекающихся
прямых, заданных двумя отрезками на боковой поверхности призмы с использованием ЛСК и с
учетом видимости.
Нанести обозначения ребер
(А,В,С) на проекциях.
Отрезки обозначить цифровыми
символами и выделить цветом.
Линии связи сохранять.

45.

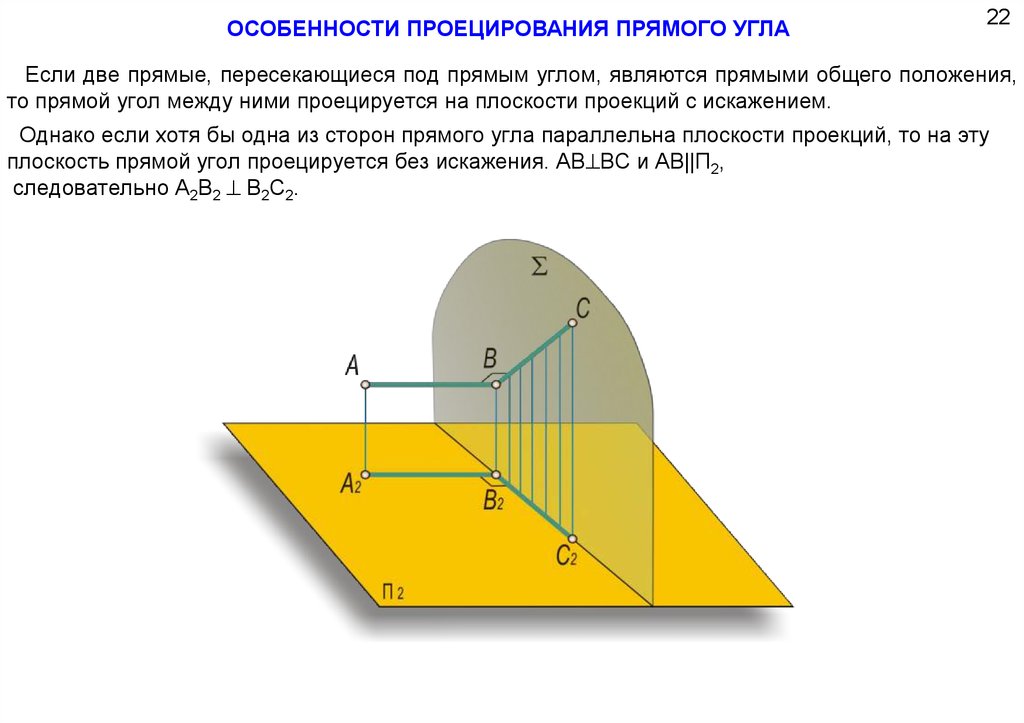
ОСОБЕННОСТИ ПРОЕЦИРОВАНИЯ ПРЯМОГО УГЛА
22
Если две прямые, пересекающиеся под прямым углом, являются прямыми общего положения,
то прямой угол между ними проецируется на плоскости проекций с искажением.
Однако если хотя бы одна из сторон прямого угла параллельна плоскости проекций, то на эту
плоскость прямой угол проецируется без искажения. АВ^ВС и АВ||П2,
следовательно А2В2 ^ В2С2.

46.

ОСОБЕННОСТИ ПРОЕЦИРОВАНИЯ ПРЯМОГО УГЛА
Задача 13. Через точку А провести прямую, перпендикулярную прямой ВС.
13.1.
13.2.
A1
В1
С1
В1
A1
С1
x12
x12
B2
С2
B2
С2
A2
A2

47.

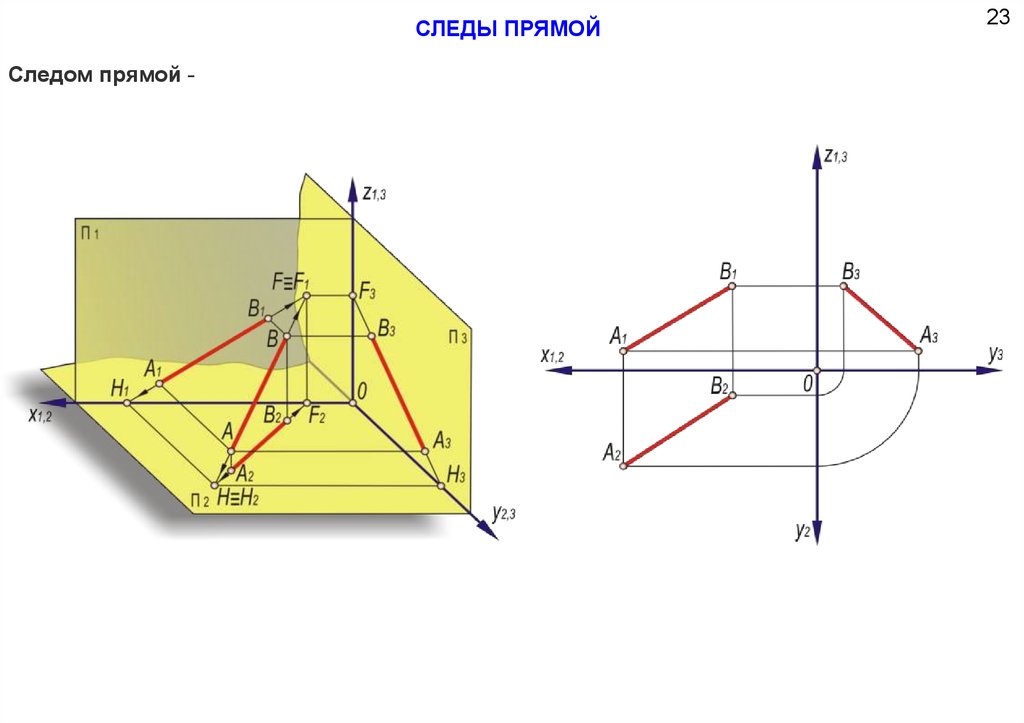
СЛЕДЫ ПРЯМОЙ
Следом прямой -.
23

48.

СЛЕДЫ ПРЯМОЙ
Задача 14. На пространственном чертеже (черт. 14.1.) и на эпюре (черт. 14.2. и 14.3.) построить
фронтальный и горизонтальный следы прямой, заданной отрезком АВ.
14.1.
1
В1
В
А1
x12
А
В2
А2
2
14.2.
14.3.
B1
A1
В1
A1
x12
x12
B2
В2
A2
A2

49.

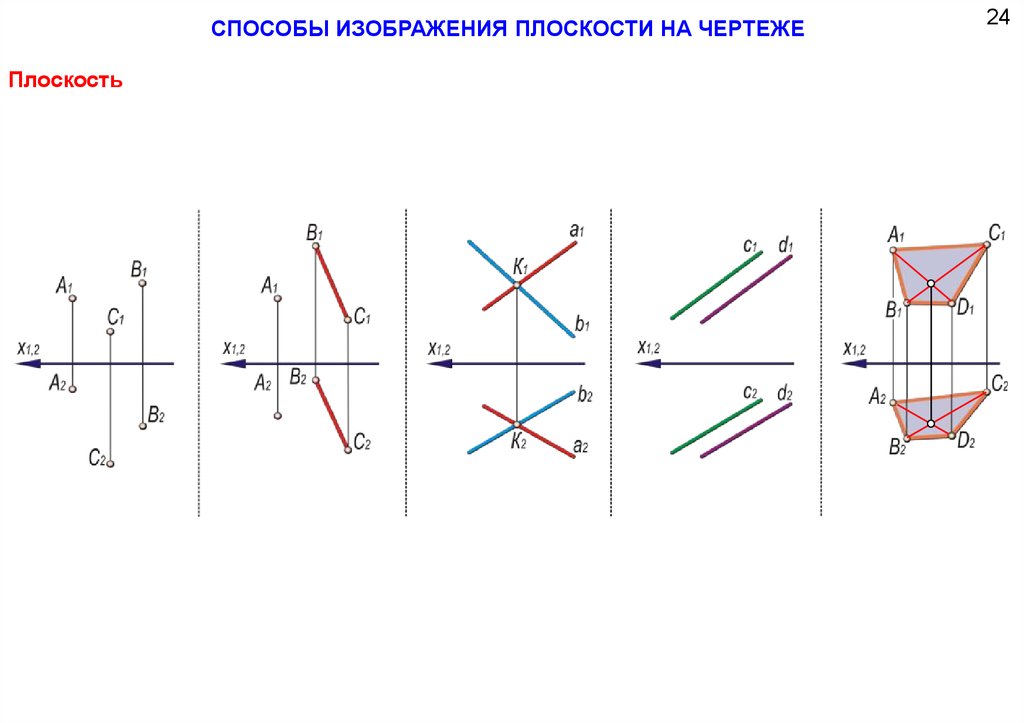
СПОСОБЫ ИЗОБРАЖЕНИЯ ПЛОСКОСТИ НА ЧЕРТЕЖЕ
Плоскость
24

50.

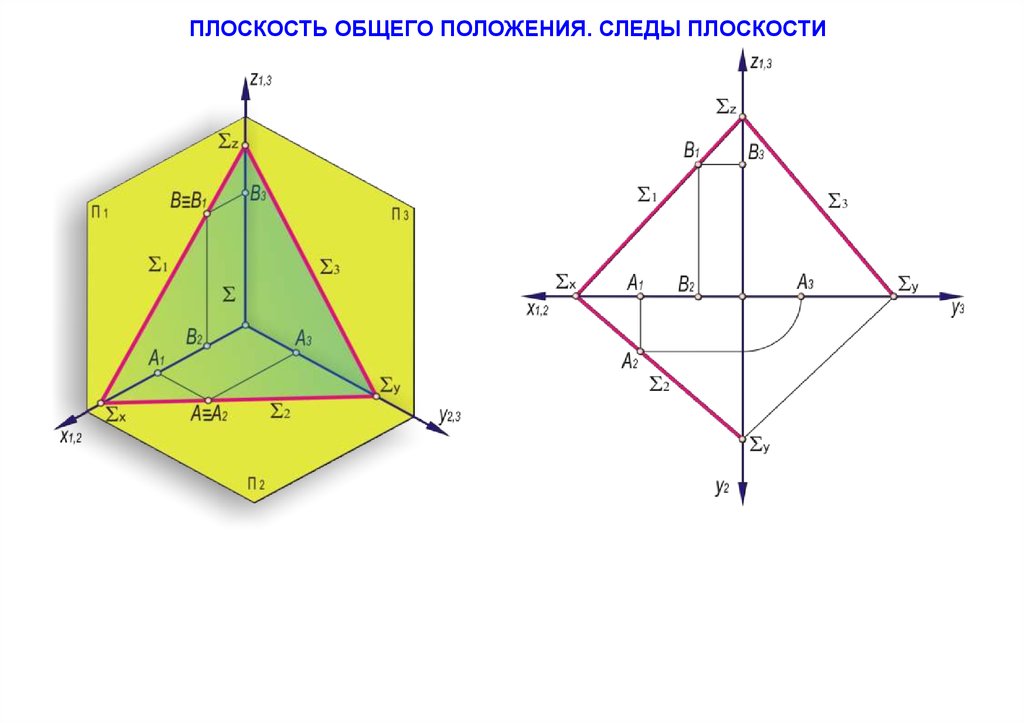
ПЛОСКОСТЬ ОБЩЕГО ПОЛОЖЕНИЯ. СЛЕДЫ ПЛОСКОСТИ

51.

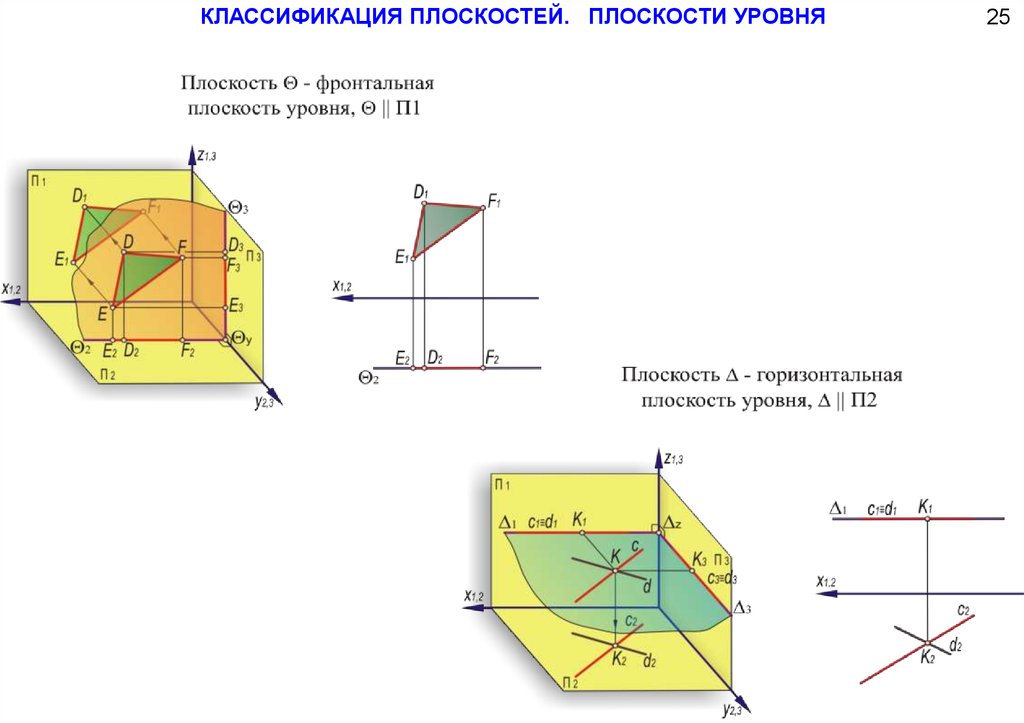
КЛАССИФИКАЦИЯ ПЛОСКОСТЕЙ. ПЛОСКОСТИ УРОВНЯ
25

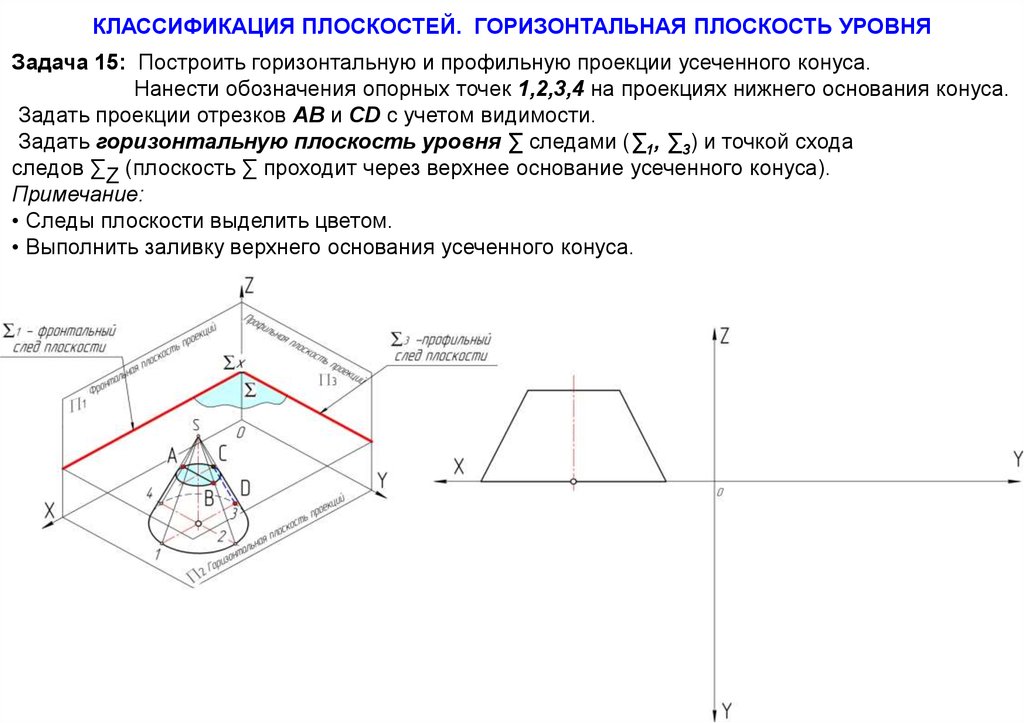
52.

КЛАССИФИКАЦИЯ ПЛОСКОСТЕЙ. ГОРИЗОНТАЛЬНАЯ ПЛОСКОСТЬ УРОВНЯ
Задача 15: Построить горизонтальную и профильную проекции усеченного конуса.
Нанести обозначения опорных точек 1,2,3,4 на проекциях нижнего основания конуса.
Задать проекции отрезков АВ и CD с учетом видимости.
Задать горизонтальную плоскость уровня ∑ следами (∑1, ∑3) и точкой схода
следов ∑Z (плоскость ∑ проходит через верхнее основание усеченного конуса).
Примечание:
• Следы плоскости выделить цветом.
• Выполнить заливку верхнего основания усеченного конуса.

53.

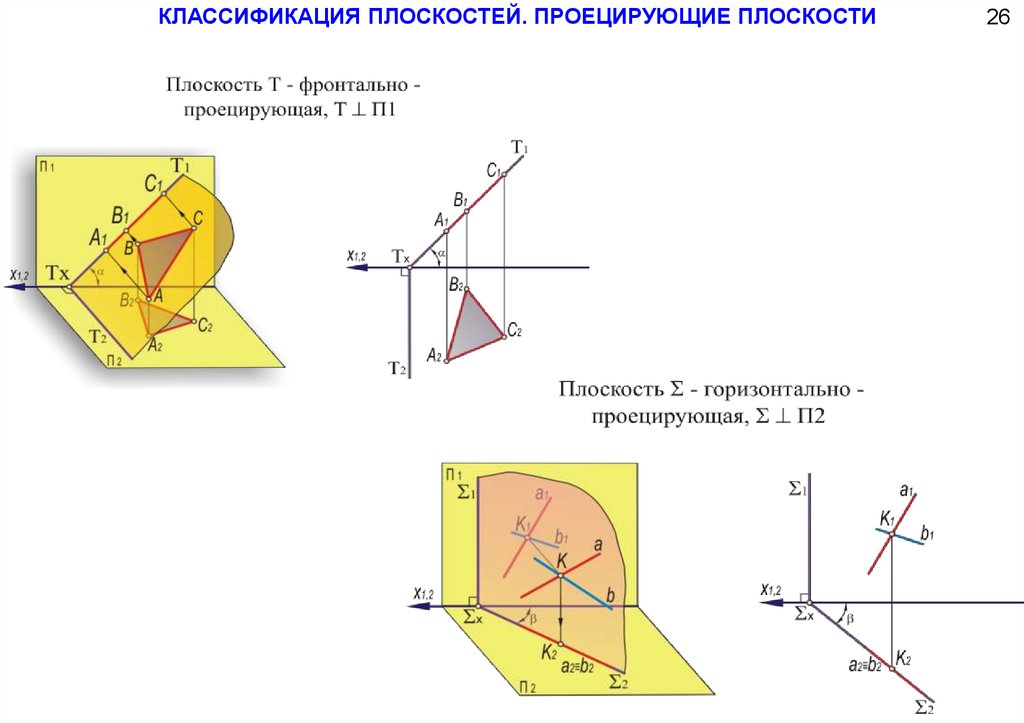
КЛАССИФИКАЦИЯ ПЛОСКОСТЕЙ. ПРОЕЦИРУЮЩИЕ ПЛОСКОСТИ
26

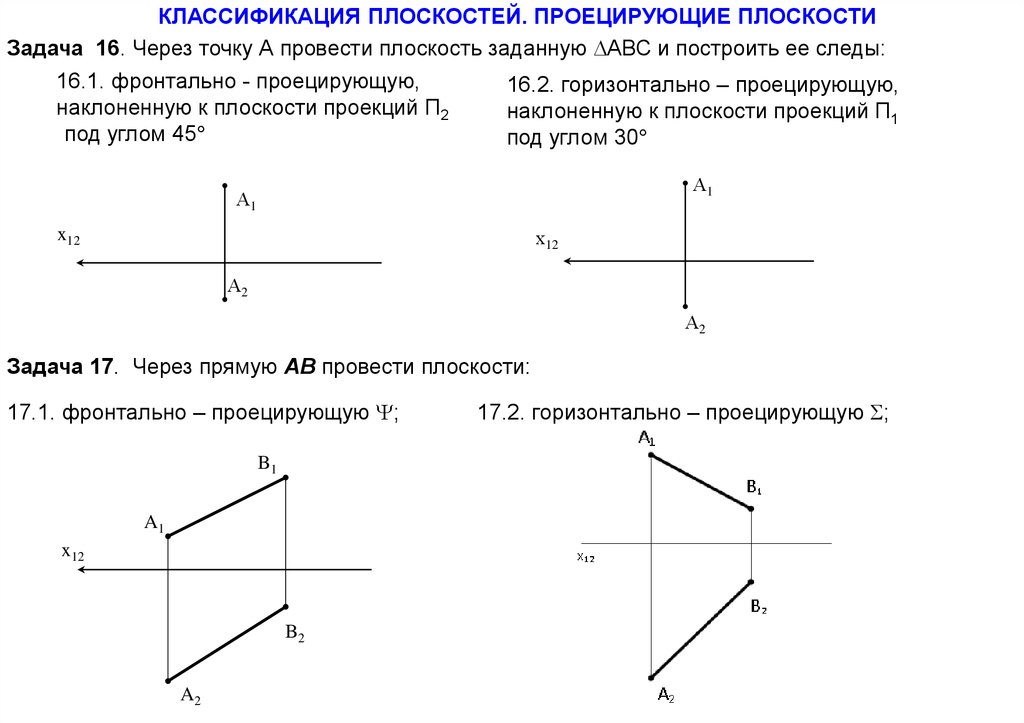
54.

КЛАССИФИКАЦИЯ ПЛОСКОСТЕЙ. ПРОЕЦИРУЮЩИЕ ПЛОСКОСТИ
Задача 16. Через точку А провести плоскость заданную АВС и построить ее следы:
16.1. фронтально - проецирующую,
16.2. горизонтально – проецирующую,
наклоненную к плоскости проекций П2
наклоненную к плоскости проекций П1
под углом 45
под углом 30
А1
А1
х12
x12
А2
А2
Задача 17. Через прямую АВ провести плоскости:
17.1. фронтально – проецирующую ;
B1
A1
x12
B2
A2
17.2. горизонтально – проецирующую ;

55.

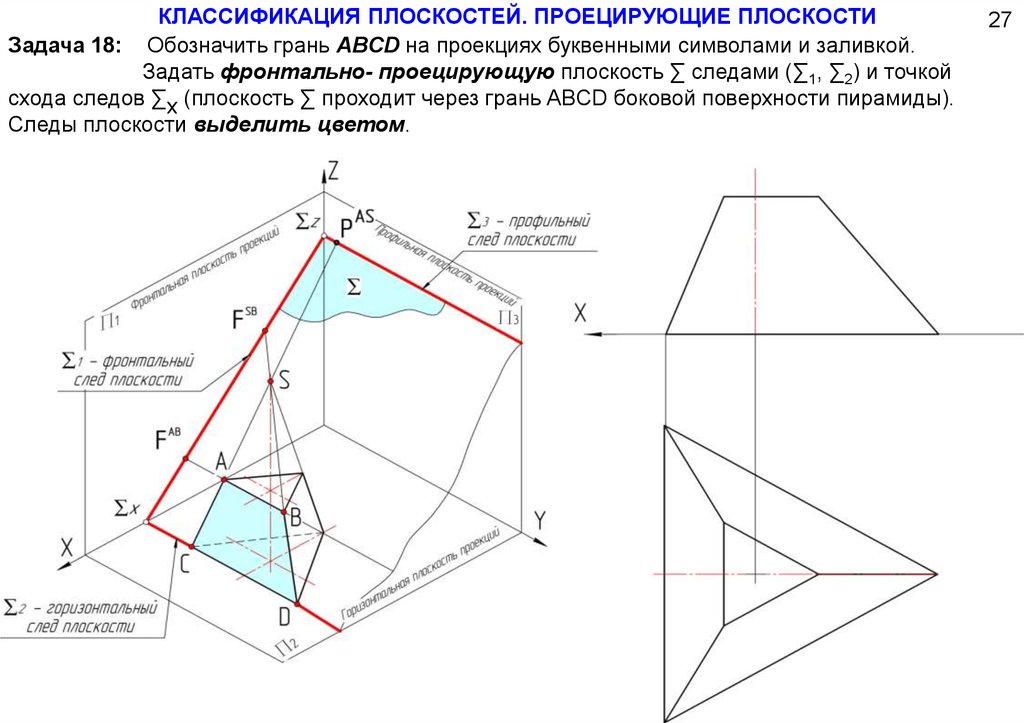
КЛАССИФИКАЦИЯ ПЛОСКОСТЕЙ. ПРОЕЦИРУЮЩИЕ ПЛОСКОСТИ
Задача 18: Обозначить грань ABCD на проекциях буквенными символами и заливкой.
Задать фронтально- проецирующую плоскость ∑ следами (∑1, ∑2) и точкой
схода следов ∑х (плоскость ∑ проходит через грань ABCD боковой поверхности пирамиды).
Следы плоскости выделить цветом.
27

56.

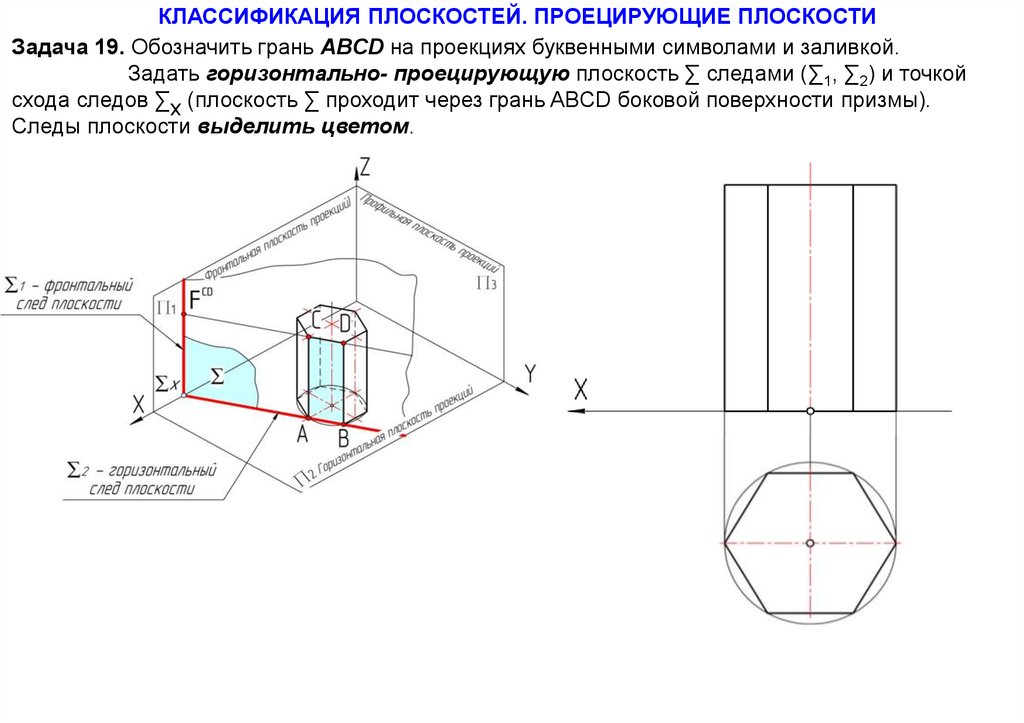
КЛАССИФИКАЦИЯ ПЛОСКОСТЕЙ. ПРОЕЦИРУЮЩИЕ ПЛОСКОСТИ
Задача 19. Обозначить грань ABCD на проекциях буквенными символами и заливкой.
Задать горизонтально- проецирующую плоскость ∑ следами (∑1, ∑2) и точкой
схода следов ∑х (плоскость ∑ проходит через грань ABCD боковой поверхности призмы).
Следы плоскости выделить цветом.

57.

ПРЯМАЯ И ТОЧКА В ПЛОСКОСТИ
28

58.

СПОСОБЫ ПРЕОБРАЗОВАНИЯ ЧЕРТЕЖА
РЕШЕНИЕ МНОГИХ ЗАДАЧ НГ ПОЛУЧАЕТСЯ БОЛЕЕ ПРОСТЫМ И БЫСТРЫМ, ЕСЛИ РАСПОЛОЖИТЬ ГЕОМЕТРИЧЕСКИЕ ЭЛЕМЕНТЫ (ГЭ) ЧАСТНЫМ ОБРАЗОМ ОТНОСИТЕЛЬНО
ПЛОСКОСТЕЙ ПРОЕКЦИЙ.
ПЕРВЫЙ СПОСОБ –
ВТОРОЙ СПОСОБ –
ЗАМЕНА ПЛОСКОСТЕЙ ПРОЕКЦИЙ
СУЩНОСТЬ СПОСОБА:
ПРАВИЛО :

59.

ОПРЕДЕЛЕНИЕ ИСТИННОЙ ВЕЛИЧИНЫ ОТРЕЗКА И УГЛА ЕГО НАКЛОНА К
ГОРИЗОНТАЛЬНОЙ ПЛОСКОСТИ ПРОЕКЦИЙ СПОСОБОМ ЗАМЕНЫ ПЛОСКОСТЕЙ
29

60.

ЗАМЕНА ПЛОСКОСТЕЙ ПРОЕКЦИЙ
Задача 20. Опустить перпендикуляр из точки А на отрезок ВС.
А1
С1
x12
П1
П2
В1
С2
А2
В2

61.

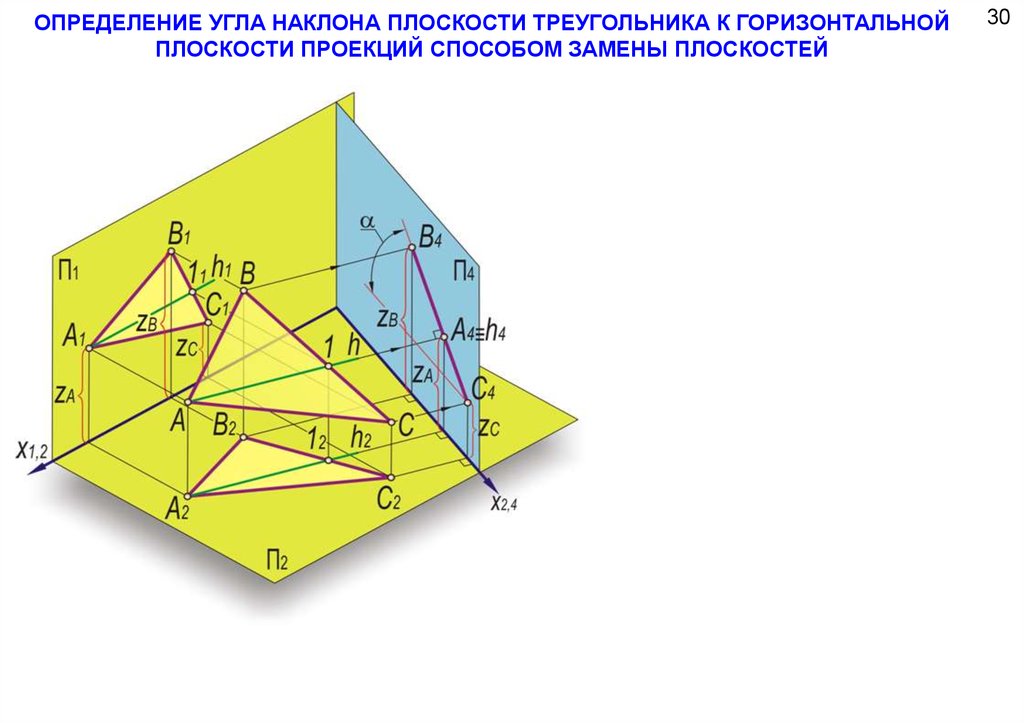
ОПРЕДЕЛЕНИЕ УГЛА НАКЛОНА ПЛОСКОСТИ ТРЕУГОЛЬНИКА К ГОРИЗОНТАЛЬНОЙ
ПЛОСКОСТИ ПРОЕКЦИЙ СПОСОБОМ ЗАМЕНЫ ПЛОСКОСТЕЙ
30

62.

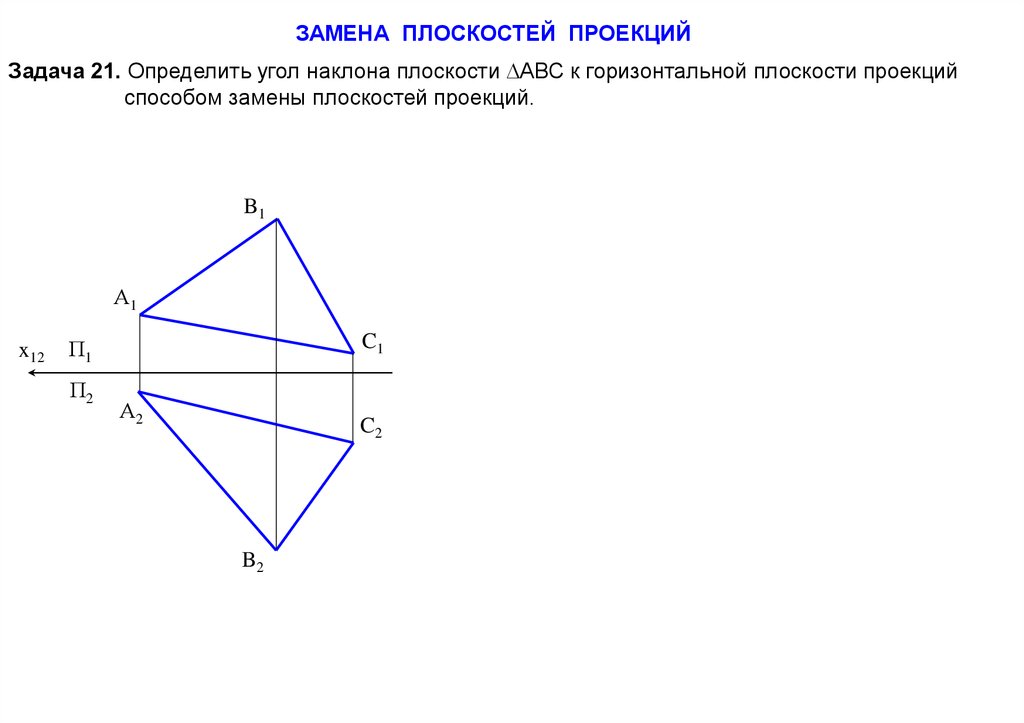
ЗАМЕНА ПЛОСКОСТЕЙ ПРОЕКЦИЙ
Задача 21. Определить угол наклона плоскости АВС к горизонтальной плоскости проекций
способом замены плоскостей проекций.
B1
А1
x12
C1
П1
П2
А2
C2
B2

63. ГОСТ 2.305-2008 ИЗОБРАЖЕНИЯ – ВИДЫ, РАЗРЕЗЫ, СЕЧЕНИЯ

РАЗРЕЗОМ
31

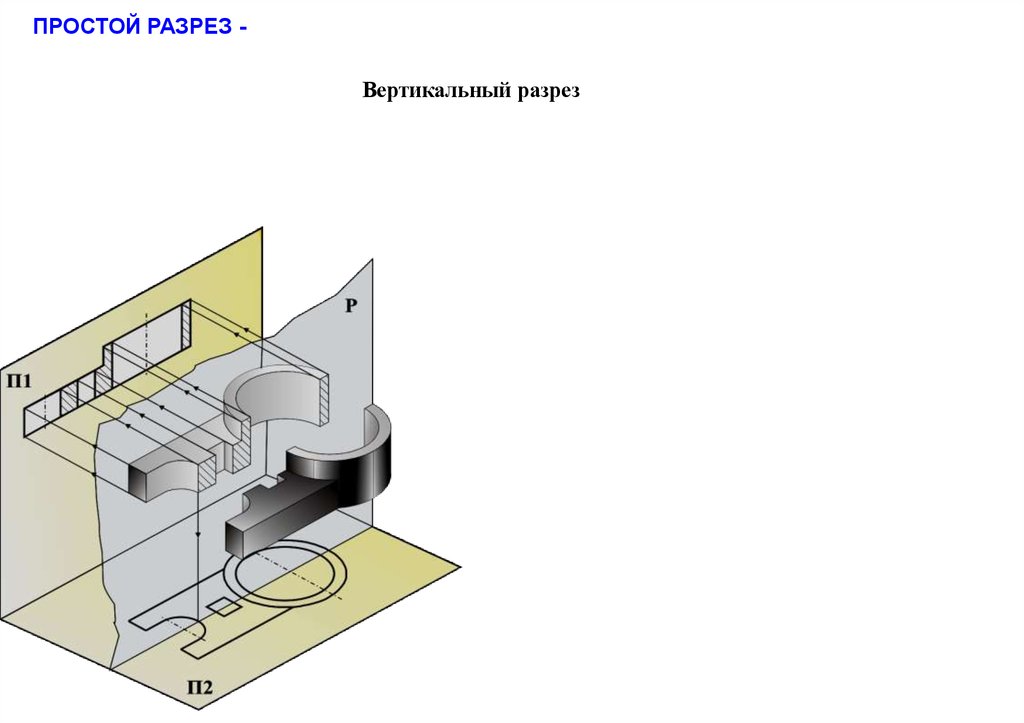
64.

ПРОСТОЙ РАЗРЕЗ -
Вертикальный разрез

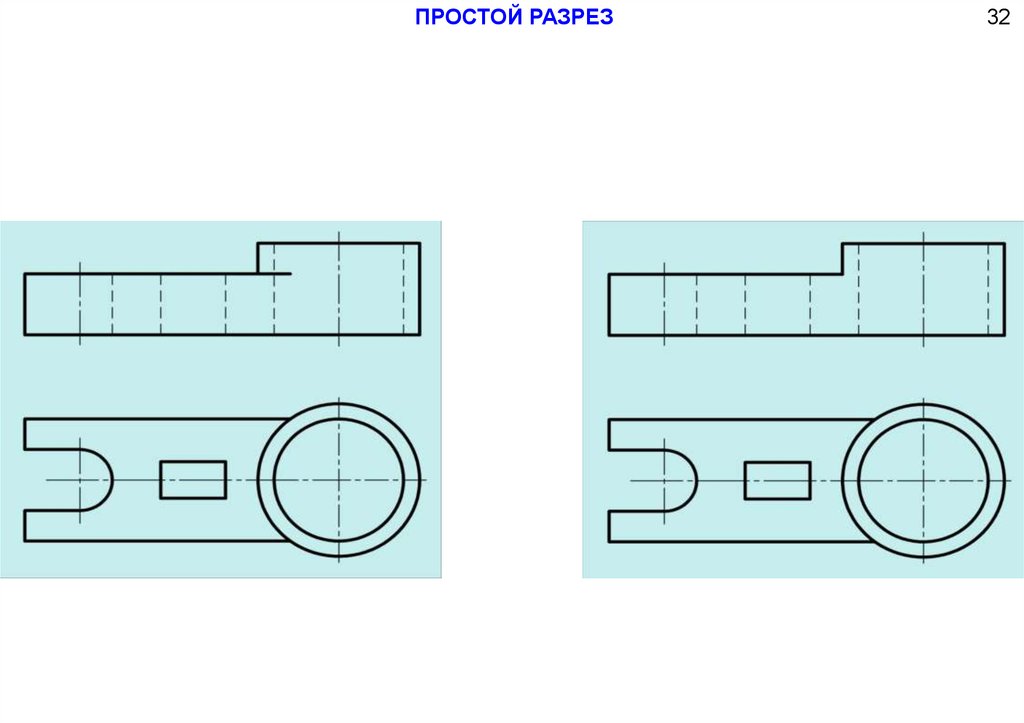
65.

ПРОСТОЙ РАЗРЕЗ
Простой фронтальный разрез
Исходный чертеж
32

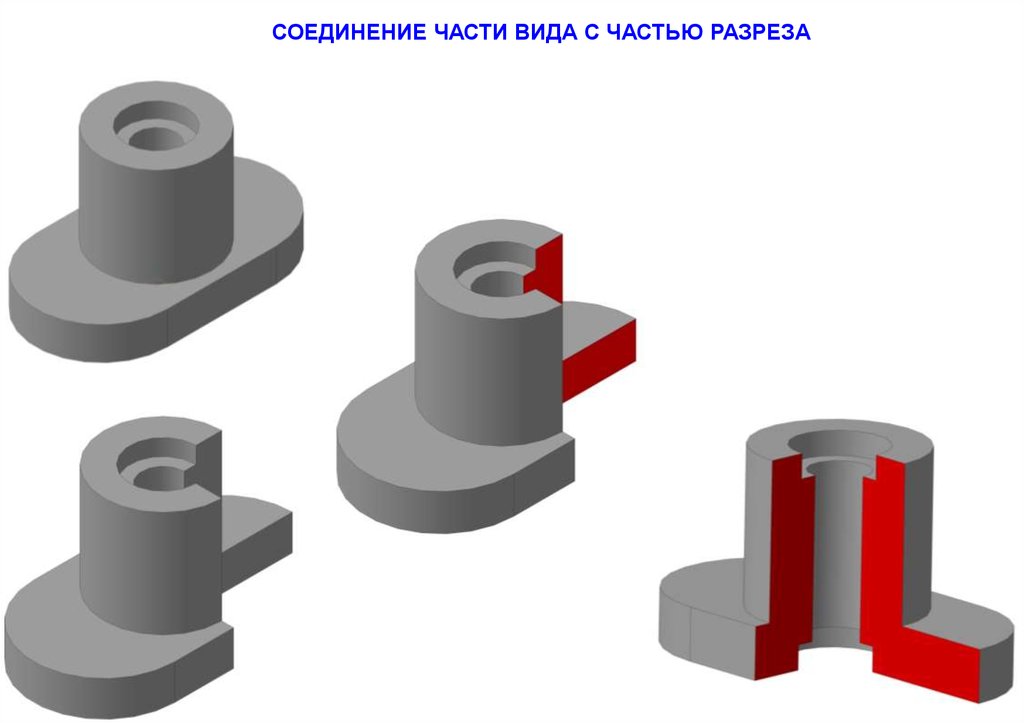
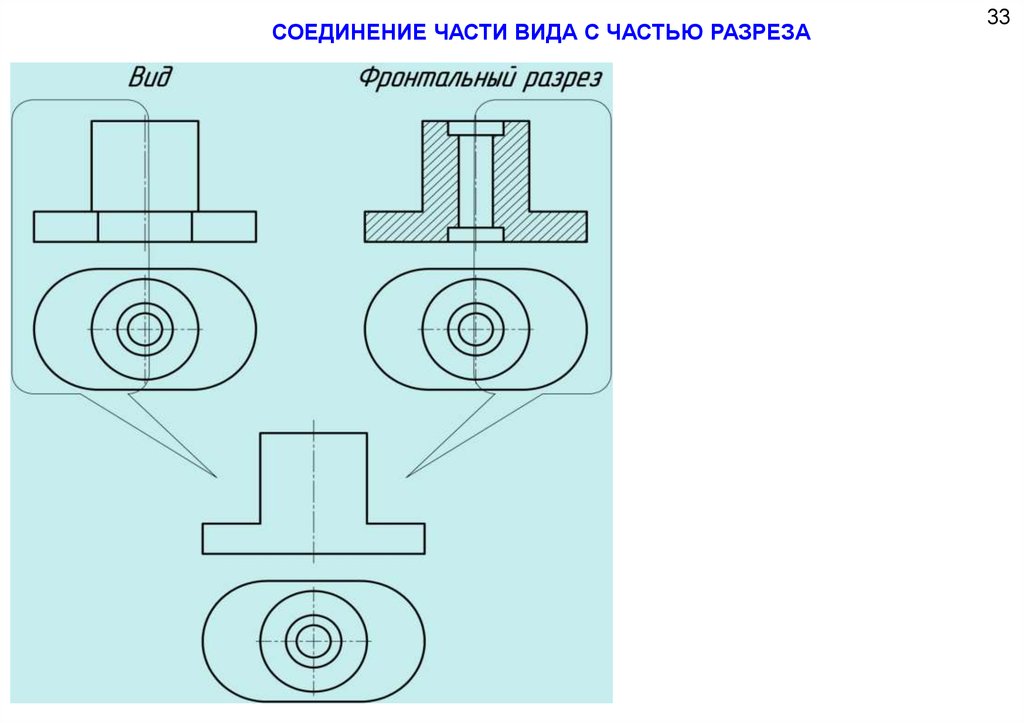
66. СОЕДИНЕНИЕ ЧАСТИ ВИДА С ЧАСТЬЮ РАЗРЕЗА

67. СОЕДИНЕНИЕ ЧАСТИ ВИДА С ЧАСТЬЮ РАЗРЕЗА

33

68.

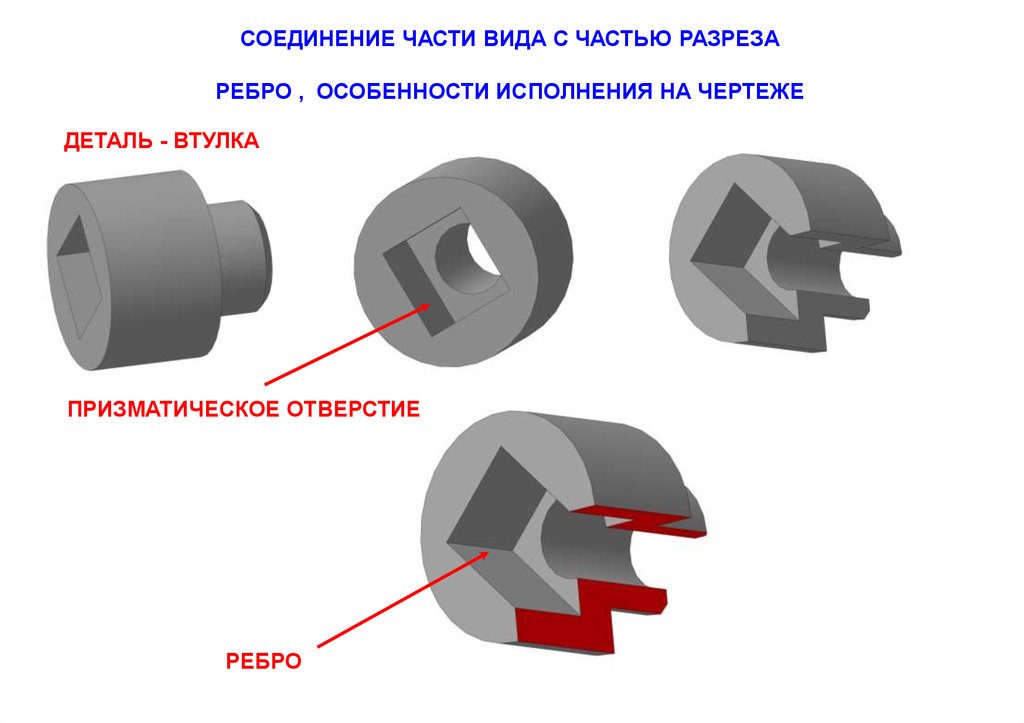
СОЕДИНЕНИЕ ЧАСТИ ВИДА С ЧАСТЬЮ РАЗРЕЗА
РЕБРО , ОСОБЕННОСТИ ИСПОЛНЕНИЯ НА ЧЕРТЕЖЕ
ДЕТАЛЬ - ВТУЛКА
ПРИЗМАТИЧЕСКОЕ ОТВЕРСТИЕ
РЕБРО

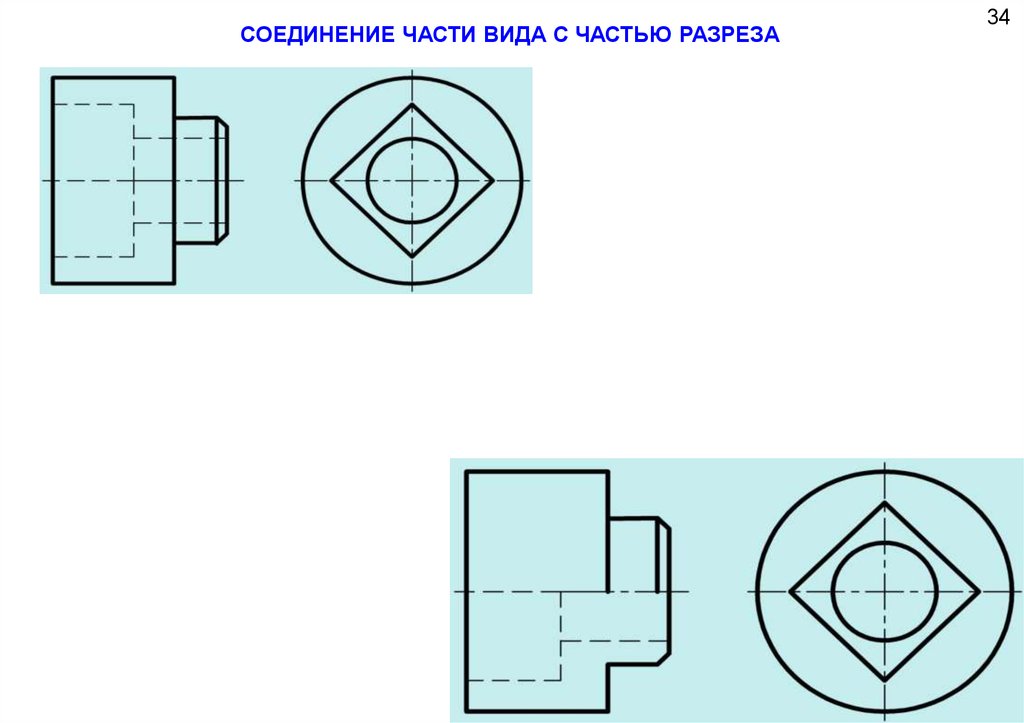
69.

СОЕДИНЕНИЕ ЧАСТИ ВИДА С ЧАСТЬЮ РАЗРЕЗА
34

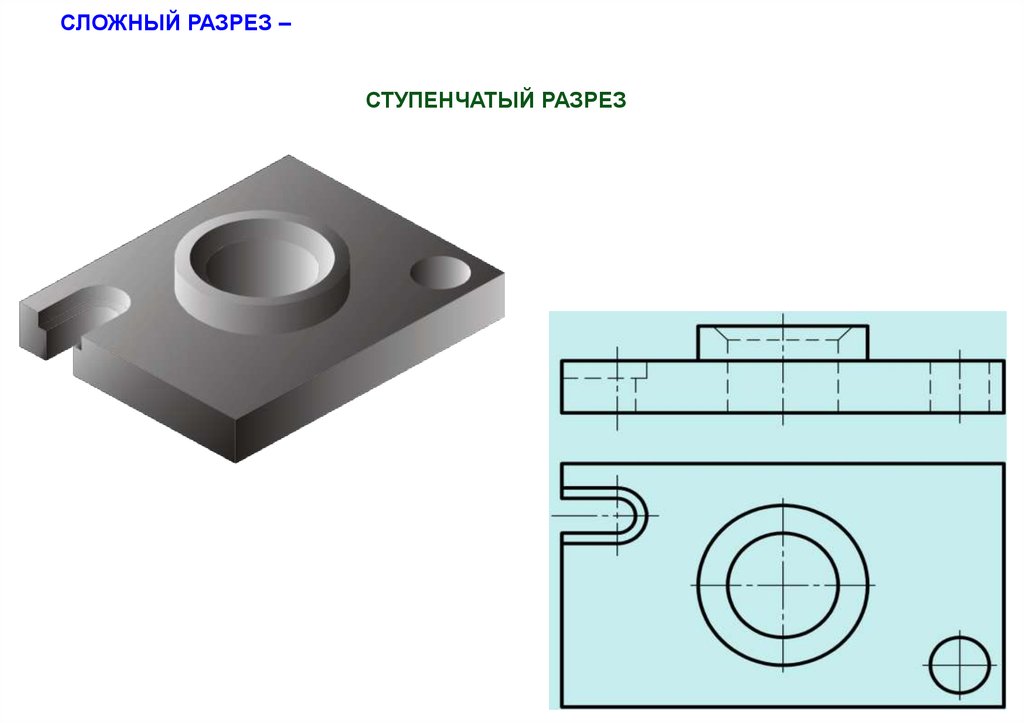
70.

СЛОЖНЫЙ РАЗРЕЗ –
СТУПЕНЧАТЫЙ РАЗРЕЗ

71.

СТУПЕНЧАТЫЙ РАЗРЕЗ
35

72.

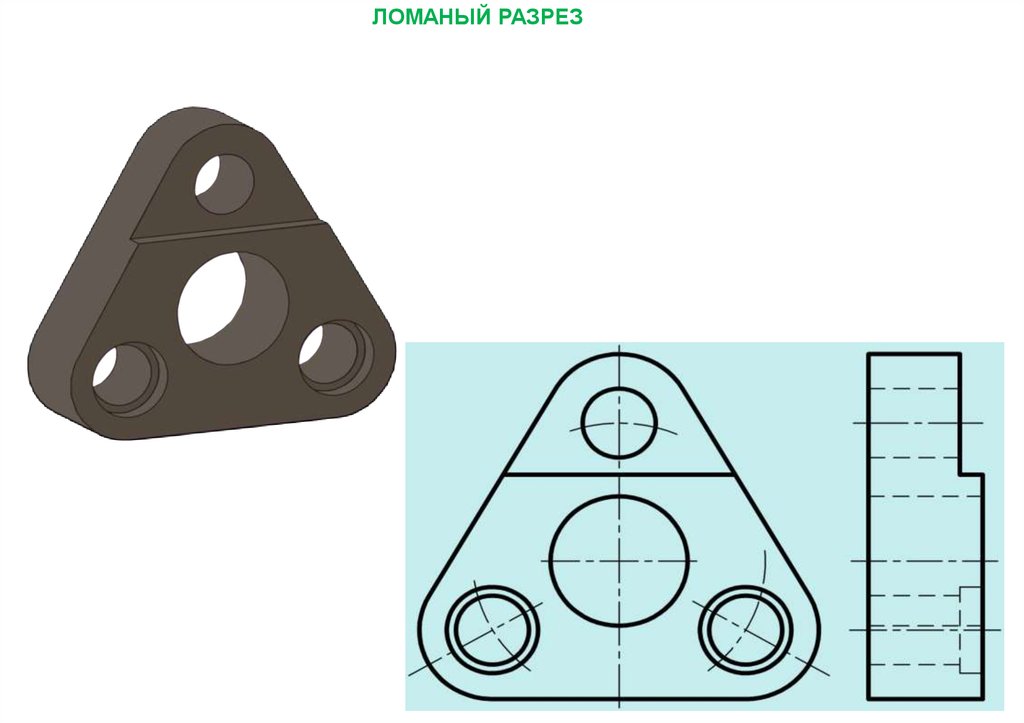
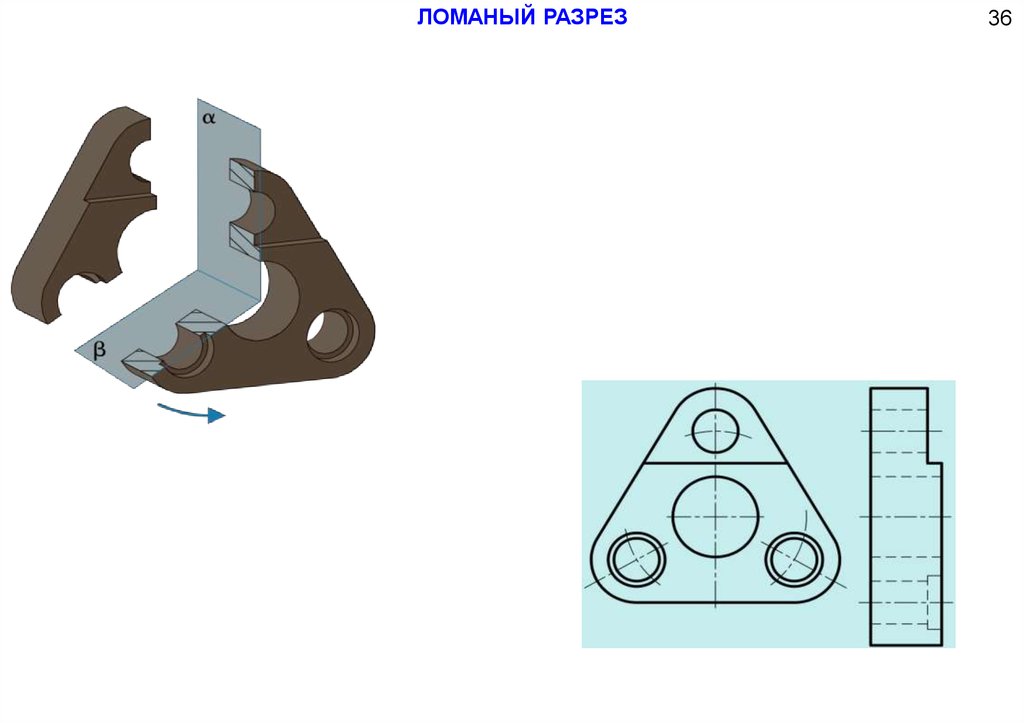
ЛОМАНЫЙ РАЗРЕЗ

73.

ЛОМАНЫЙ РАЗРЕЗ
36

74.

ПОВЕРХНОСТИ
В НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ ПОВЕРХНОСТИ РАССМАТРИВАЮТ С ТОЧКИ ЗРЕНИЯ
СПОСОБА ОБРАЗОВАНИЯ:
НА ЭПЮРЕ МОНЖА ПОВЕРХНОСТЬ ЗАДАЕТСЯ:
КЛАССИФИКАЦИЯ ПОВЕРХНОСТЕЙ
ЛИНЕЙЧАТЫЕ
97

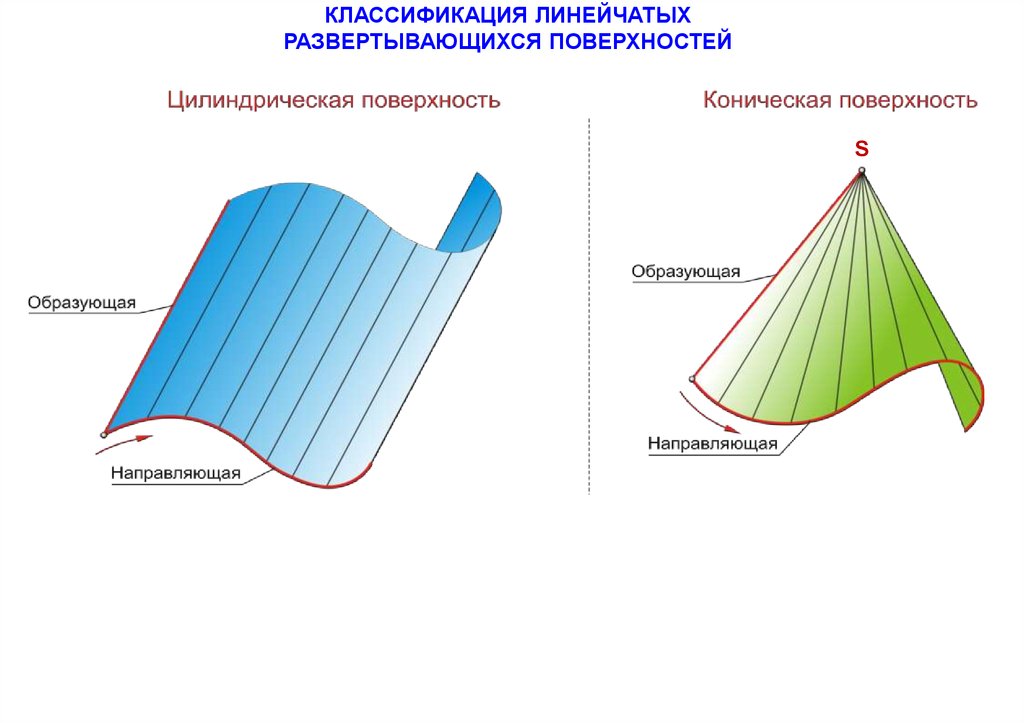
75.

КЛАССИФИКАЦИЯ ЛИНЕЙЧАТЫХ
РАЗВЕРТЫВАЮЩИХСЯ ПОВЕРХНОСТЕЙ
37
37
S

76.

КЛАССИФИКАЦИЯ ЛИНЕЙЧАТЫХ
РАЗВЕРТЫВАЮЩИХСЯ ПОВЕРХНОСТЕЙ
98
S

77.

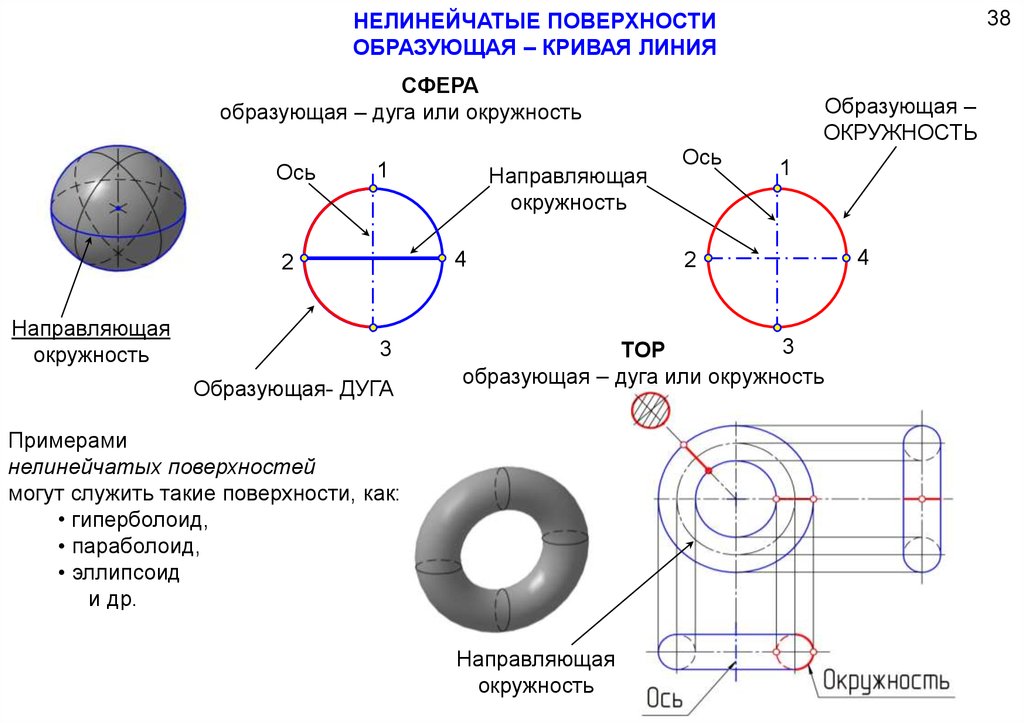
НЕЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ
ОБРАЗУЮЩАЯ – КРИВАЯ ЛИНИЯ
38
СФЕРА
образующая – дуга или окружность
Ось
1
4
2
Направляющая
окружность
Направляющая
окружность
3
Образующая- ДУГА
Образующая –
ОКРУЖНОСТЬ
Ось
1
2
3
ТОР
образующая – дуга или окружность
Примерами
нелинейчатых поверхностей
могут служить такие поверхности, как:
• гиперболоид,
• параболоид,
• эллипсоид
и др.
Направляющая
окружность
4

78.

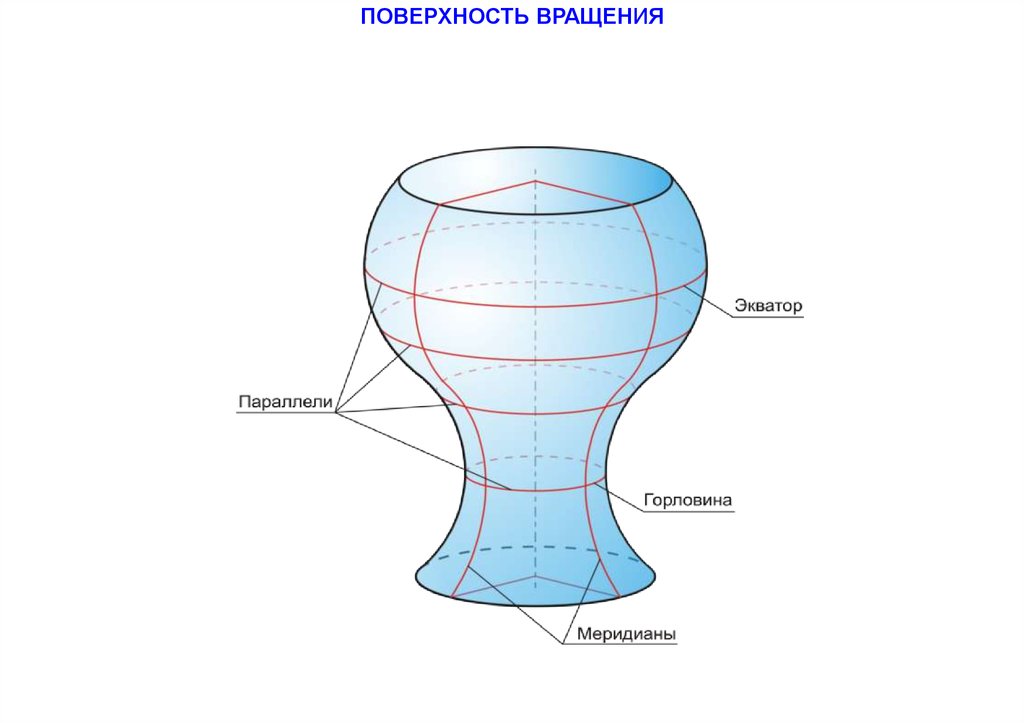
ПОВЕРХНОСТЬ ВРАЩЕНИЯ
К ПОВЕРХНОСТЯМ ВРАЩЕНИЯ ОТНОСЯТСЯ ПОВЕРХНОСТИ, ОБРАЗУЮЩИЕСЯ
ВРАЩЕНИЕМ ЛИНИИ ВОКРУГ ПРЯМОЙ , ПРЕДСТАВЛЯЮЩЕЙ СОБОЙ ОСЬ ВРАЩЕНИЯ
100

79.

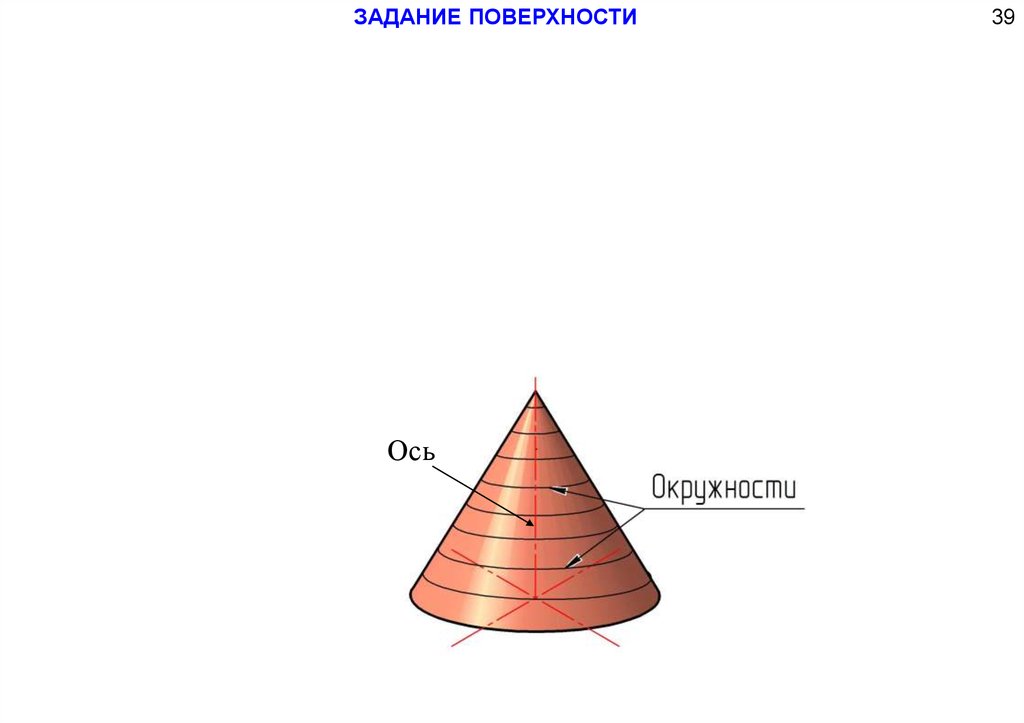
ЗАДАНИЕ ПОВЕРХНОСТИ
Ось
101
39

80.

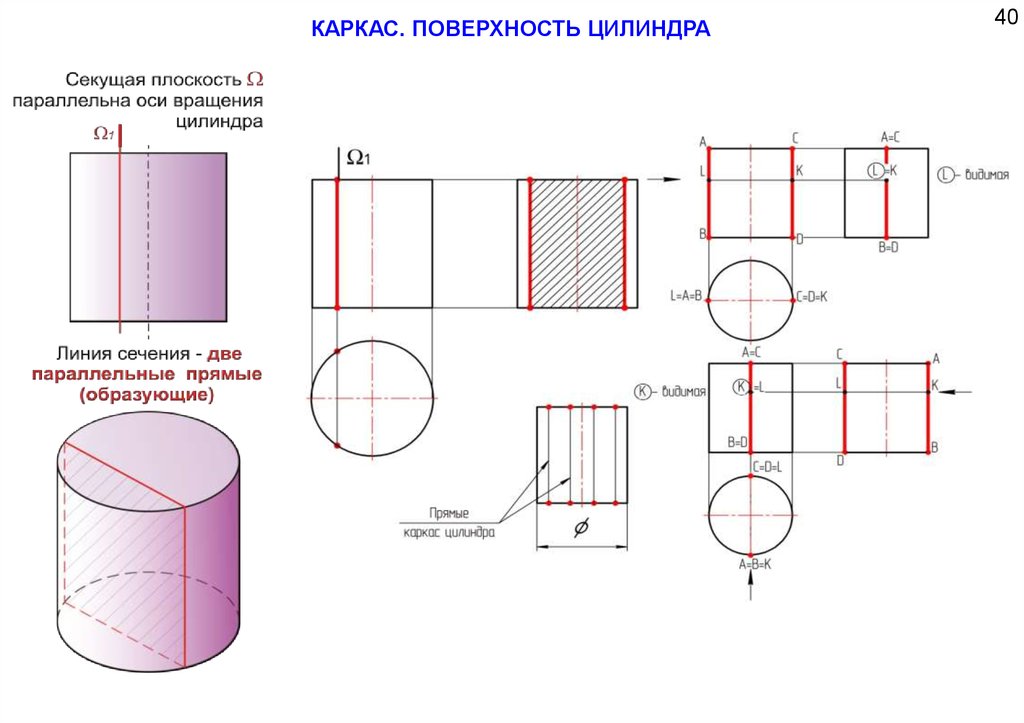
ПОВЕРХНОСТИ ВРАЩЕНИЯ

81.

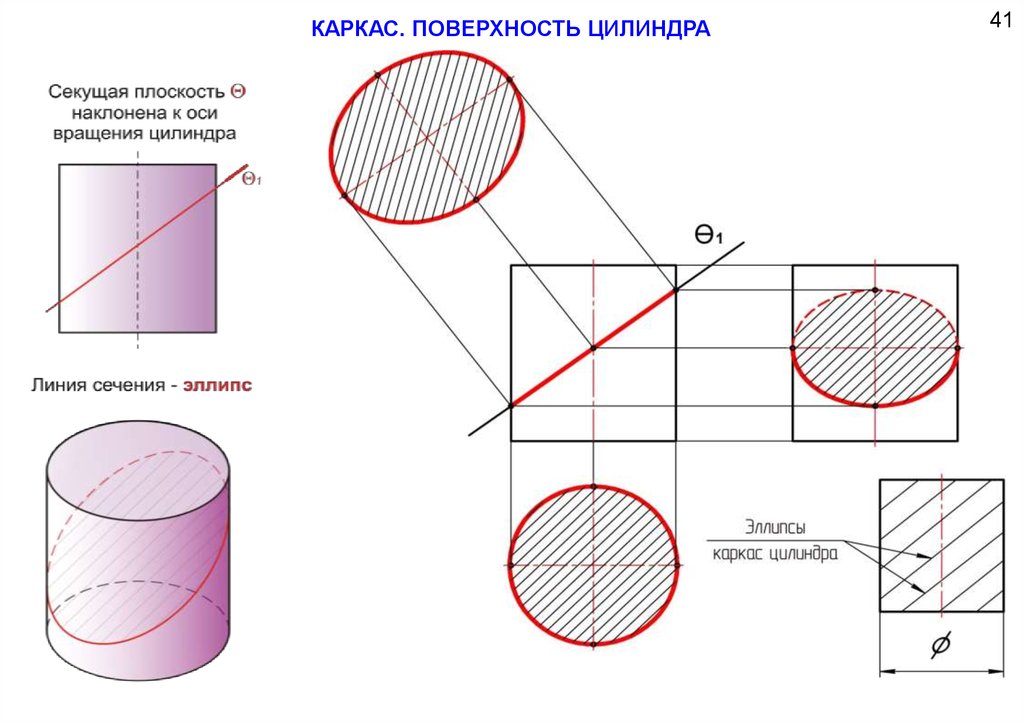
КАРКАС. ПОВЕРХНОСТЬ ЦИЛИНДРА
40

82.

КАРКАС. ПОВЕРХНОСТЬ ЦИЛИНДРА

83.

КАРКАС. ПОВЕРХНОСТЬ ЦИЛИНДРА
41

84.

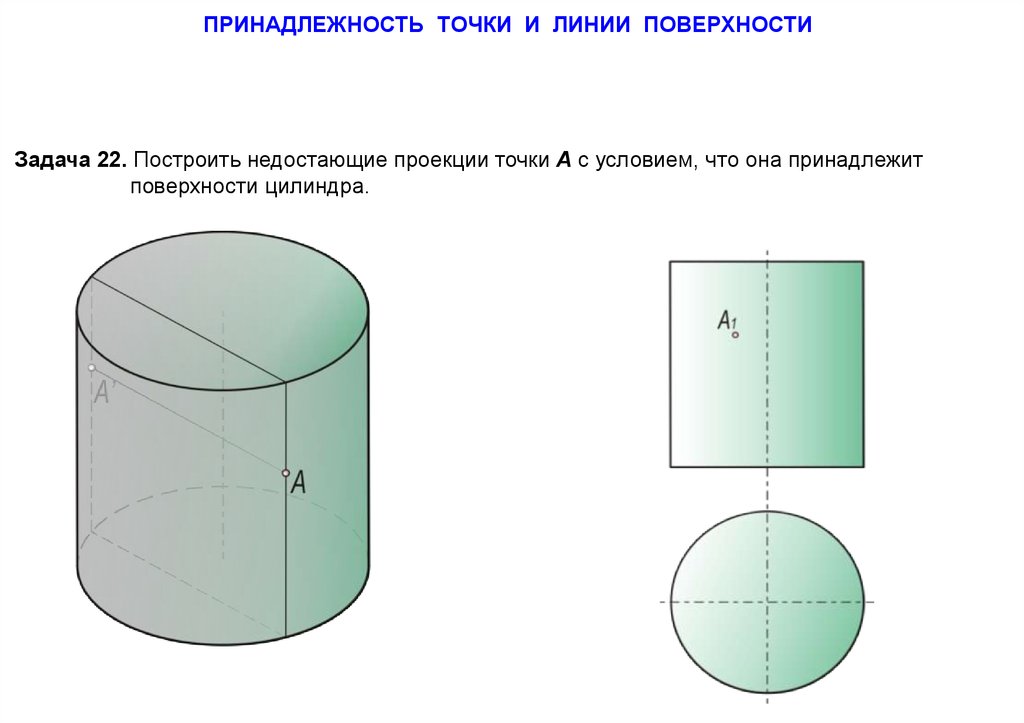
ПРИНАДЛЕЖНОСТЬ ТОЧКИ И ЛИНИИ ПОВЕРХНОСТИ
Задача 22. Построить недостающие проекции точки А с условием, что она принадлежит
поверхности цилиндра.

85.

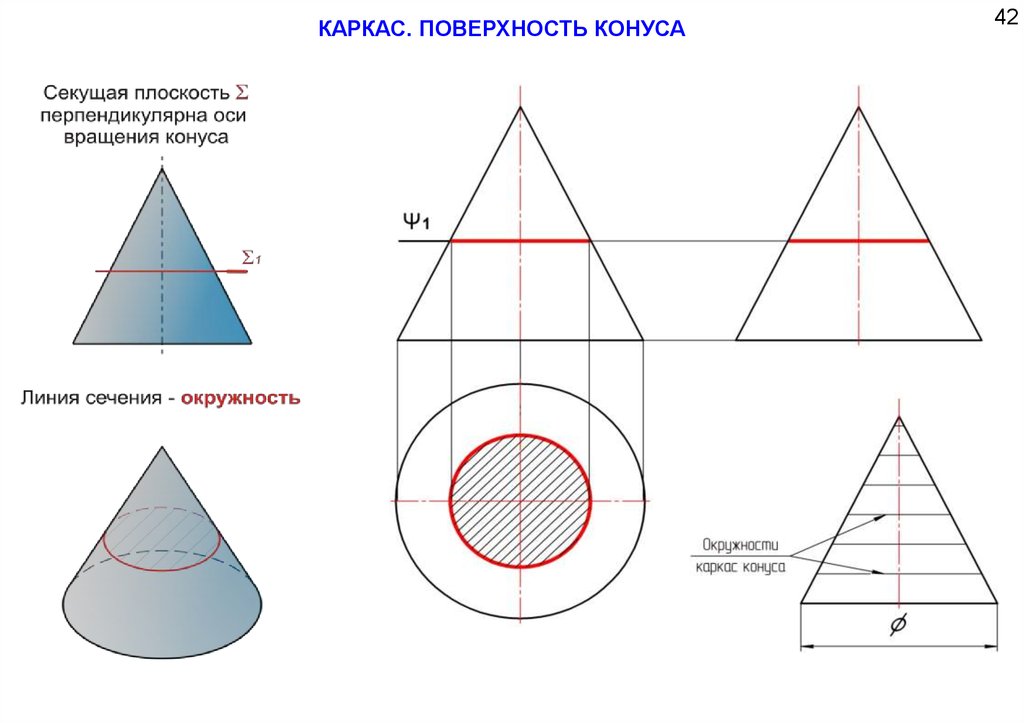
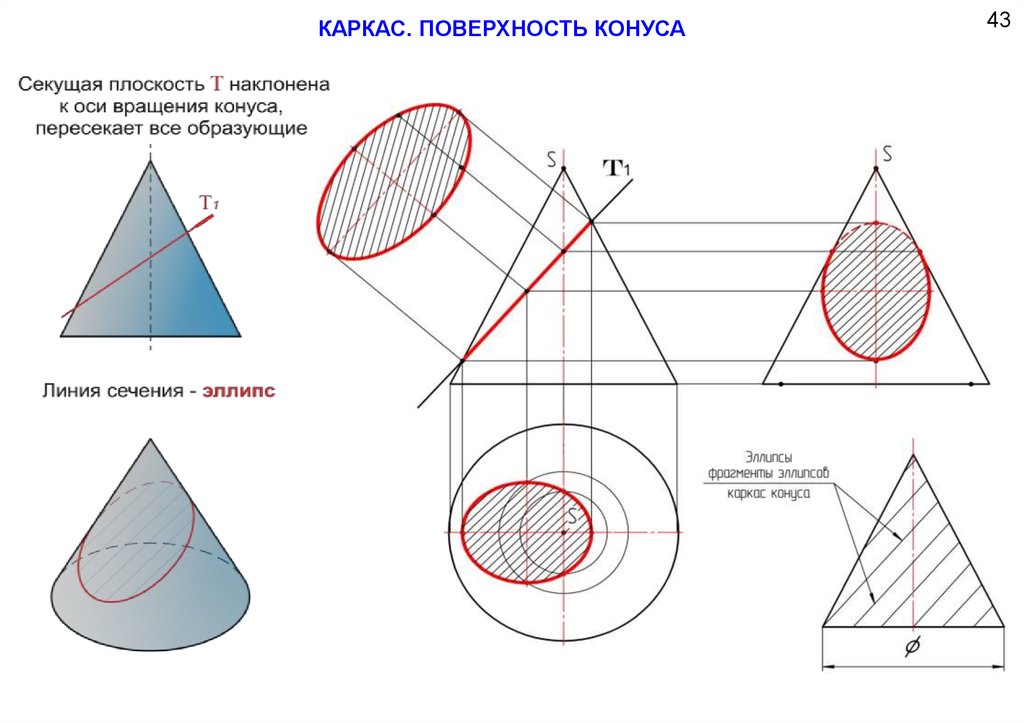
КАРКАС. ПОВЕРХНОСТЬ КОНУСА
42

86.

КАРКАС. ПОВЕРХНОСТЬ КОНУСА
45

87.

КАРКАС. ПОВЕРХНОСТЬ КОНУСА
43

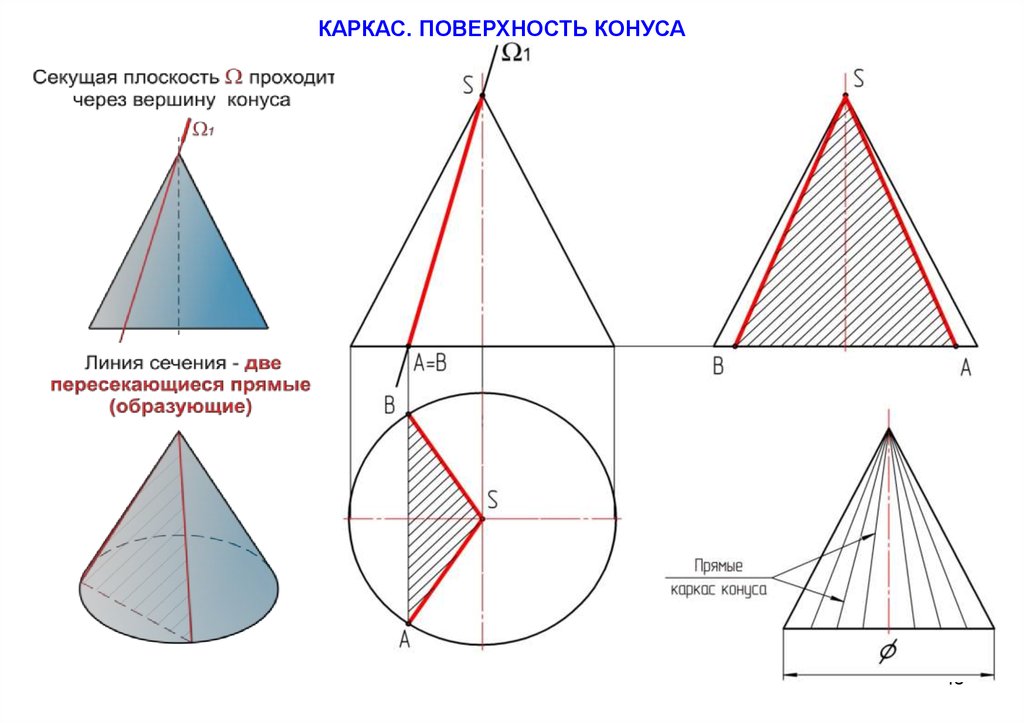
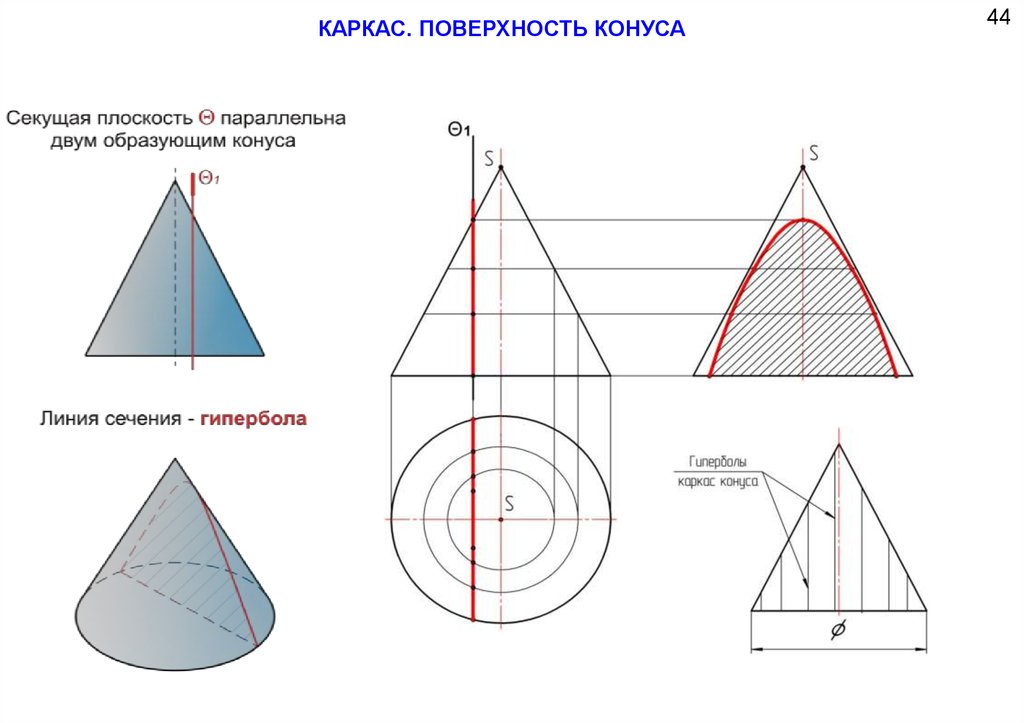
88.

КАРКАС. ПОВЕРХНОСТЬ КОНУСА

89.

КАРКАС. ПОВЕРХНОСТЬ КОНУСА
44

90.

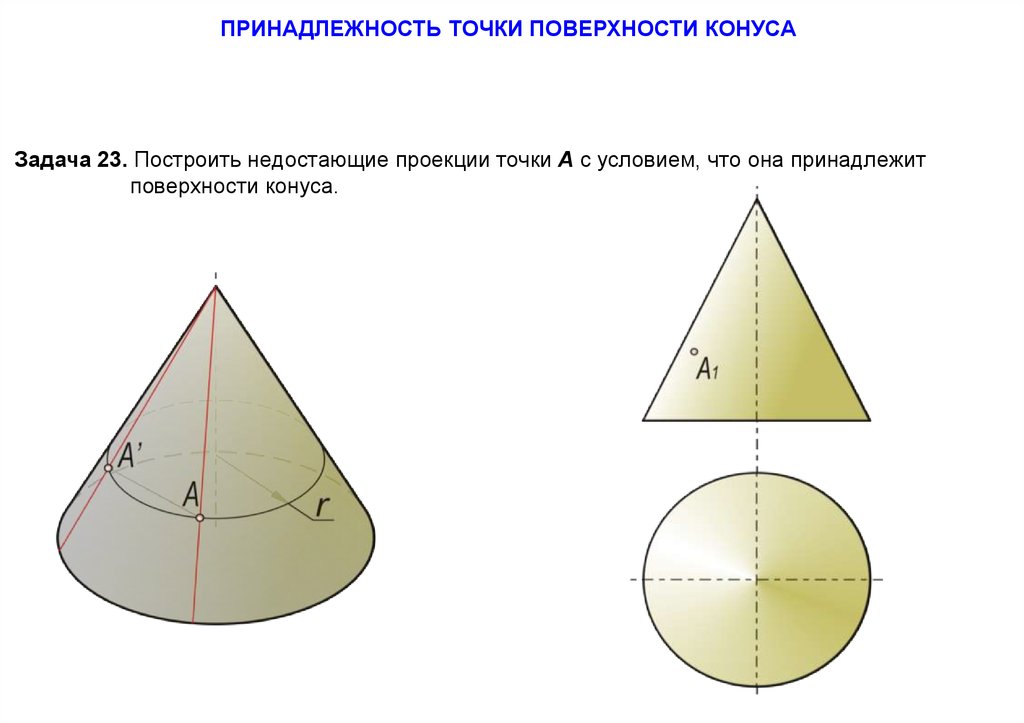
ПРИНАДЛЕЖНОСТЬ ТОЧКИ ПОВЕРХНОСТИ КОНУСА
Задача 23. Построить недостающие проекции точки А с условием, что она принадлежит
поверхности конуса.
705

91.

ПОВЕРХНОСТИ ВРАЩЕНИЯ
ЧАСТНЫЕ ВИДЫ ПОВЕРХНОСТЕЙ ВРАЩЕНИЯ
ТОР – поверхность, образованная вращением окружности или дуги окружности вокруг оси,
лежащей в одной плоскости с образующей тора, но не проходящей через ее центр
45

92.

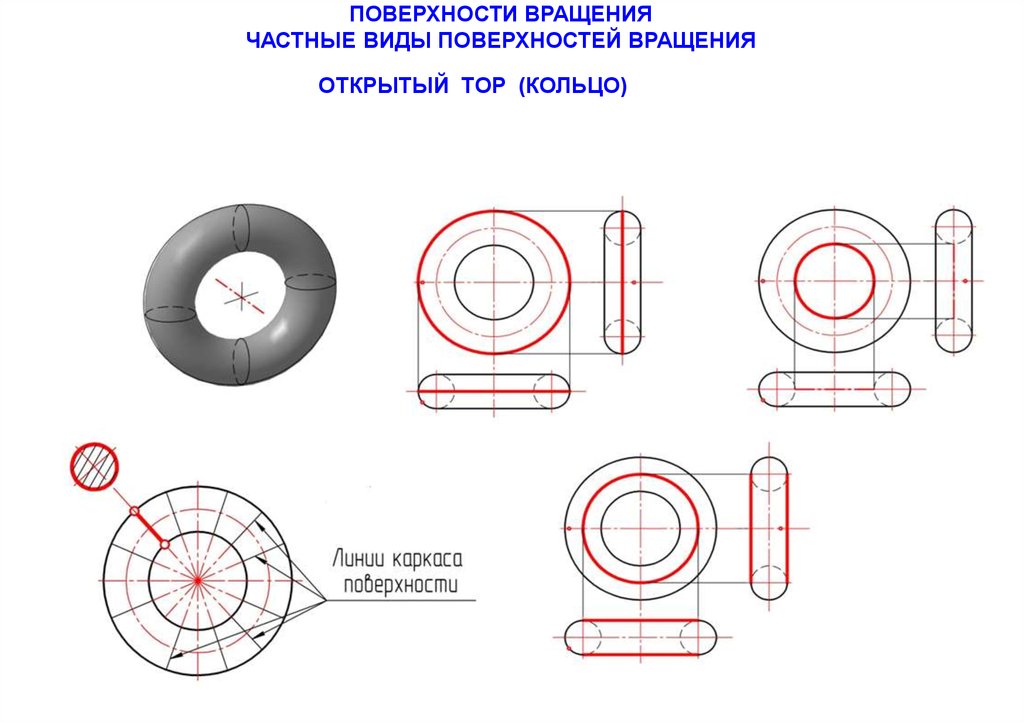
ПОВЕРХНОСТИ ВРАЩЕНИЯ
ЧАСТНЫЕ ВИДЫ ПОВЕРХНОСТЕЙ ВРАЩЕНИЯ
ОТКРЫТЫЙ ТОР (КОЛЬЦО)

93.

ПОВЕРХНОСТИ ВРАЩЕНИЯ
ЧАСТНЫЕ ВИДЫ ПОВЕРХНОСТЕЙ ВРАЩЕНИЯ
ЗАКРЫТЫЙ ТОР
46

94.

ПОВЕРХНОСТИ ВРАЩЕНИЯ
ЧАСТНЫЕ ВИДЫ ПОВЕРХНОСТЕЙ ВРАЩЕНИЯ
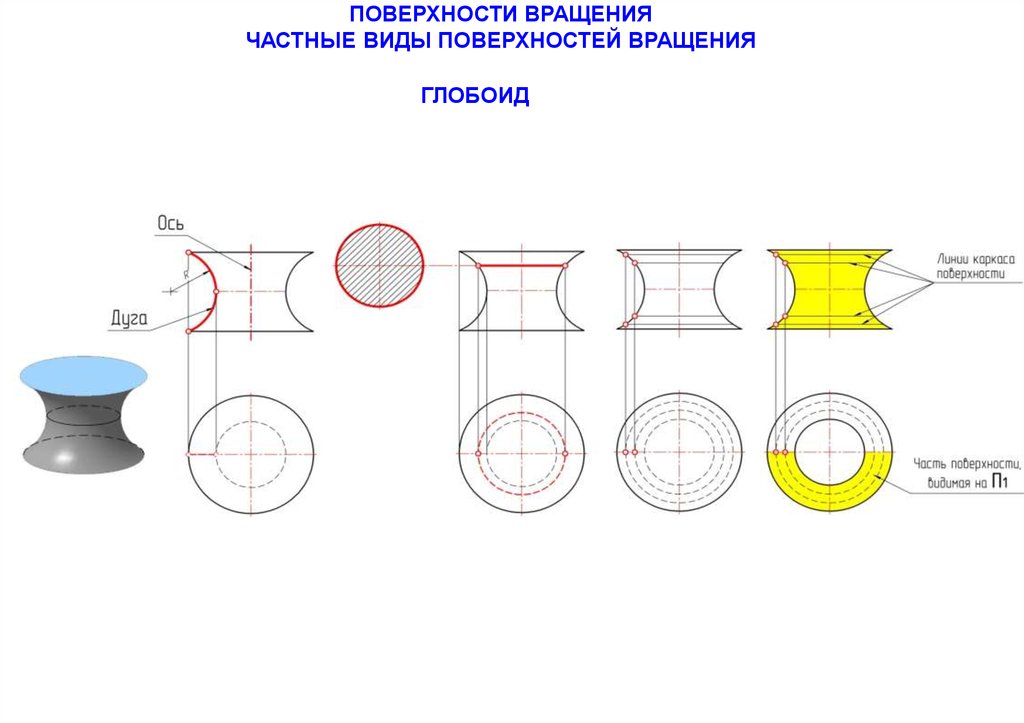
ГЛОБОИД

95.

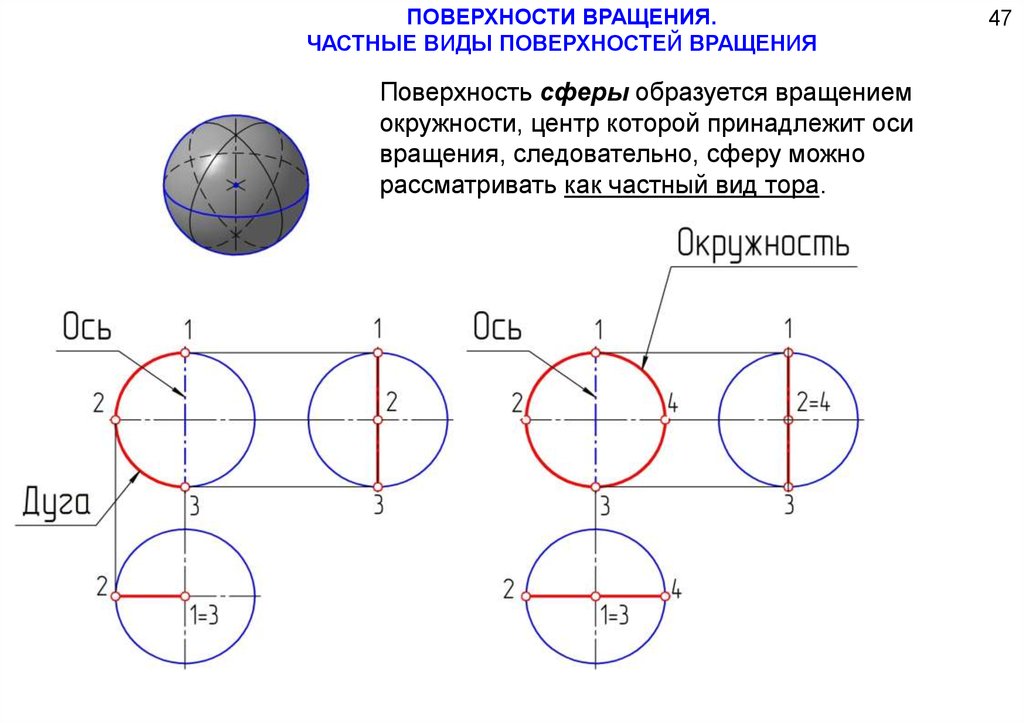
ПОВЕРХНОСТИ ВРАЩЕНИЯ.
ЧАСТНЫЕ ВИДЫ ПОВЕРХНОСТЕЙ ВРАЩЕНИЯ
Поверхность сферы образуется вращением
окружности, центр которой принадлежит оси
вращения, следовательно, сферу можно
рассматривать как частный вид тора.
47

96.

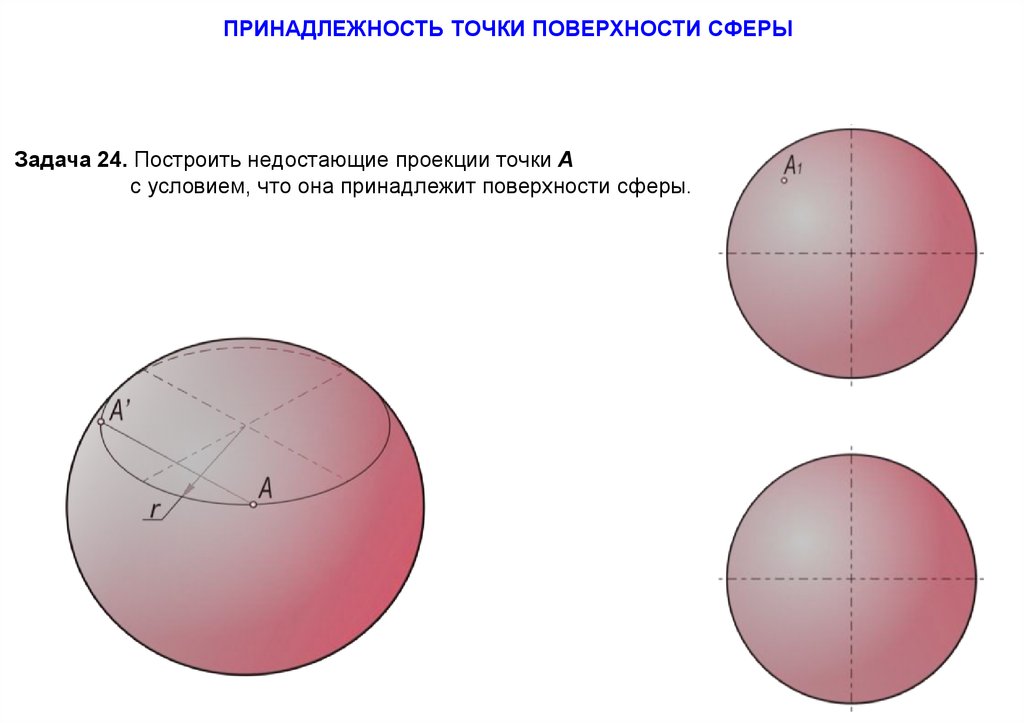
ПРИНАДЛЕЖНОСТЬ ТОЧКИ ПОВЕРХНОСТИ СФЕРЫ
Задача 24. Построить недостающие проекции точки А
с условием, что она принадлежит поверхности сферы.

97.

ГОСТ 2.305-2008 ИЗОБРАЖЕНИЯ – ВИДЫ, РАЗРЕЗЫ, СЕЧЕНИЯ
СЕЧЕНИЕМ
48

98.

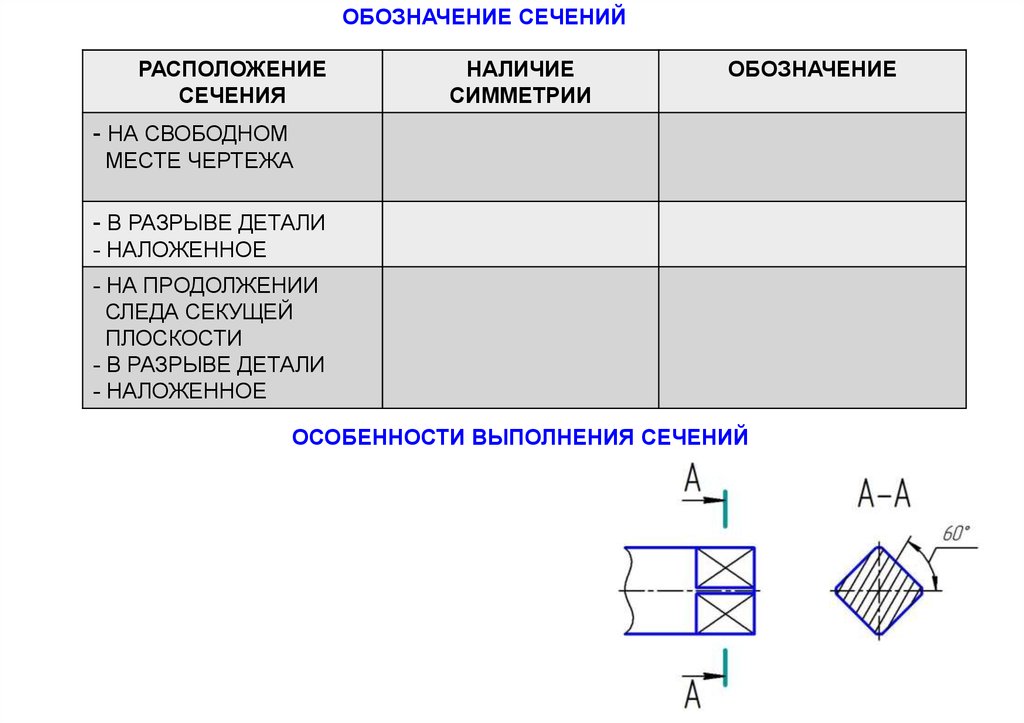
ОБОЗНАЧЕНИЕ СЕЧЕНИЙ
РАСПОЛОЖЕНИЕ
СЕЧЕНИЯ
НАЛИЧИЕ
СИММЕТРИИ
ОБОЗНАЧЕНИЕ
- НА СВОБОДНОМ
МЕСТЕ ЧЕРТЕЖА
- В РАЗРЫВЕ ДЕТАЛИ
- НАЛОЖЕННОЕ
- НА ПРОДОЛЖЕНИИ
СЛЕДА СЕКУЩЕЙ
ПЛОСКОСТИ
- В РАЗРЫВЕ ДЕТАЛИ
- НАЛОЖЕННОЕ
ОСОБЕННОСТИ ВЫПОЛНЕНИЯ СЕЧЕНИЙ

99.

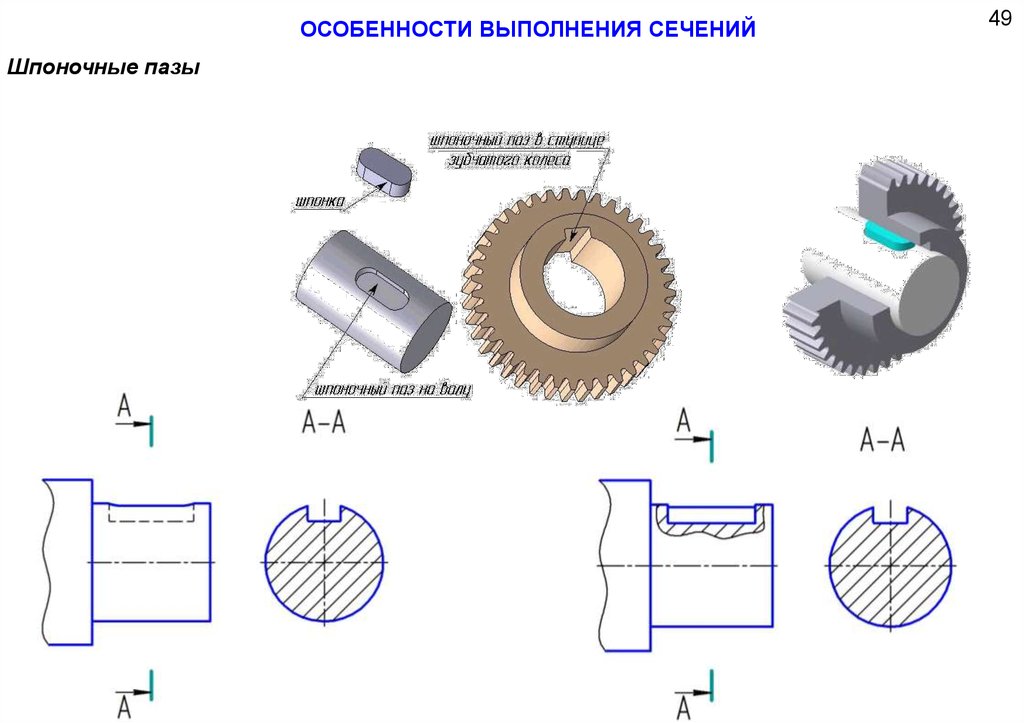
ОСОБЕННОСТИ ВЫПОЛНЕНИЯ СЕЧЕНИЙ
Шпоночные пазы
49

100.

ОСОБЕННОСТИ ВЫПОЛНЕНИЯ СЕЧЕНИЙ
Отверстия на ступени вала
ВЫНЕСЕННОЕ (НАКЛОННОЕ) СЕЧЕНИЕ

101.

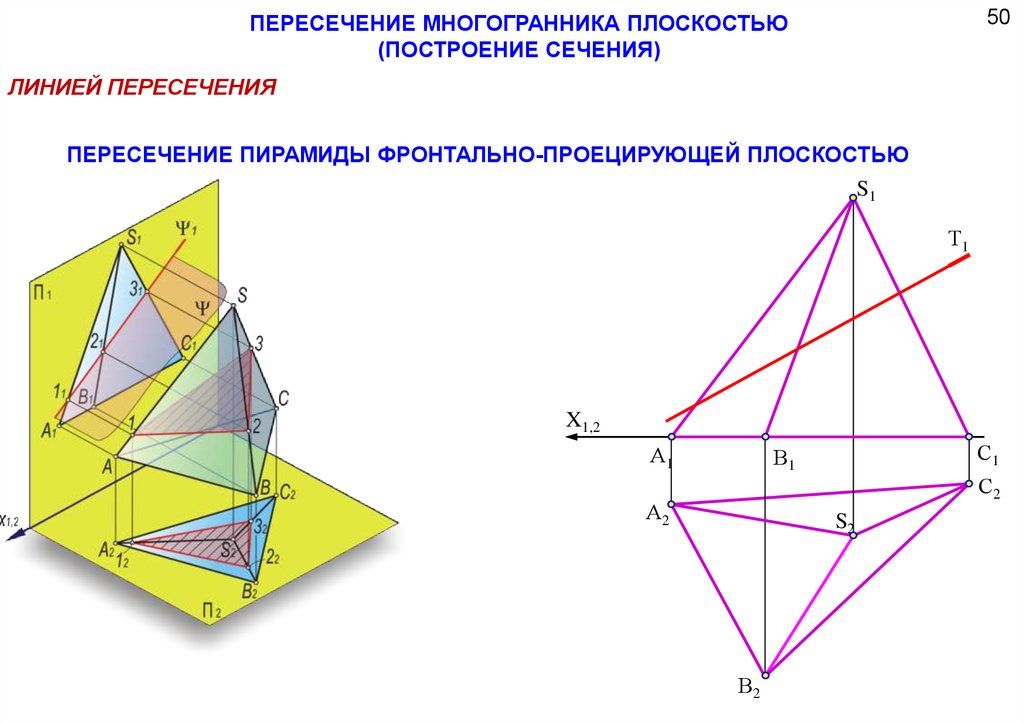
50
ПЕРЕСЕЧЕНИЕ МНОГОГРАННИКА ПЛОСКОСТЬЮ
(ПОСТРОЕНИЕ СЕЧЕНИЯ)
ЛИНИЕЙ ПЕРЕСЕЧЕНИЯ
ПЕРЕСЕЧЕНИЕ ПИРАМИДЫ ФРОНТАЛЬНО-ПРОЕЦИРУЮЩЕЙ ПЛОСКОСТЬЮ
S1
Т1
X1,2
А1
С1
В1
С2
А2
S2
В2

102.

СЕЧЕНИЕ ПОВЕРХНОСТИ СФЕРЫ ПЛОСКОСТЬЮ

103.

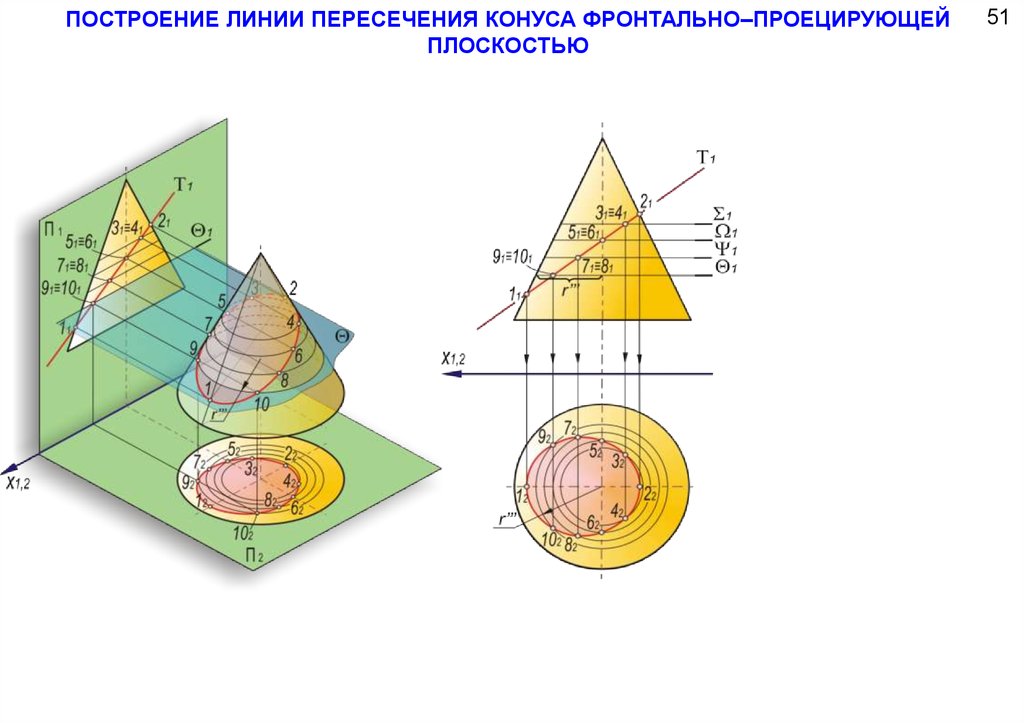
ПОСТРОЕНИЕ ЛИНИИ ПЕРЕСЕЧЕНИЯ КОНУСА ФРОНТАЛЬНО–ПРОЕЦИРУЮЩЕЙ
ПЛОСКОСТЬЮ
51

104.

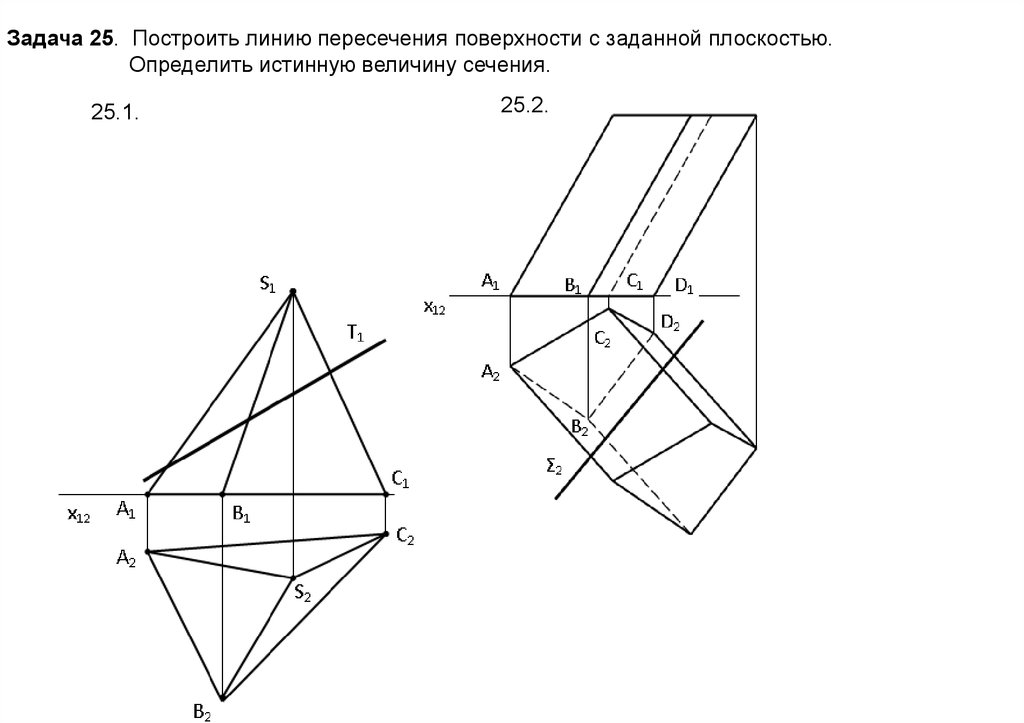
Задача 25. Построить линию пересечения поверхности с заданной плоскостью.
Определить истинную величину сечения.
25.1.
25.2.

105.

52
25.3.
25.4
S1
Ψ1
S2

106.

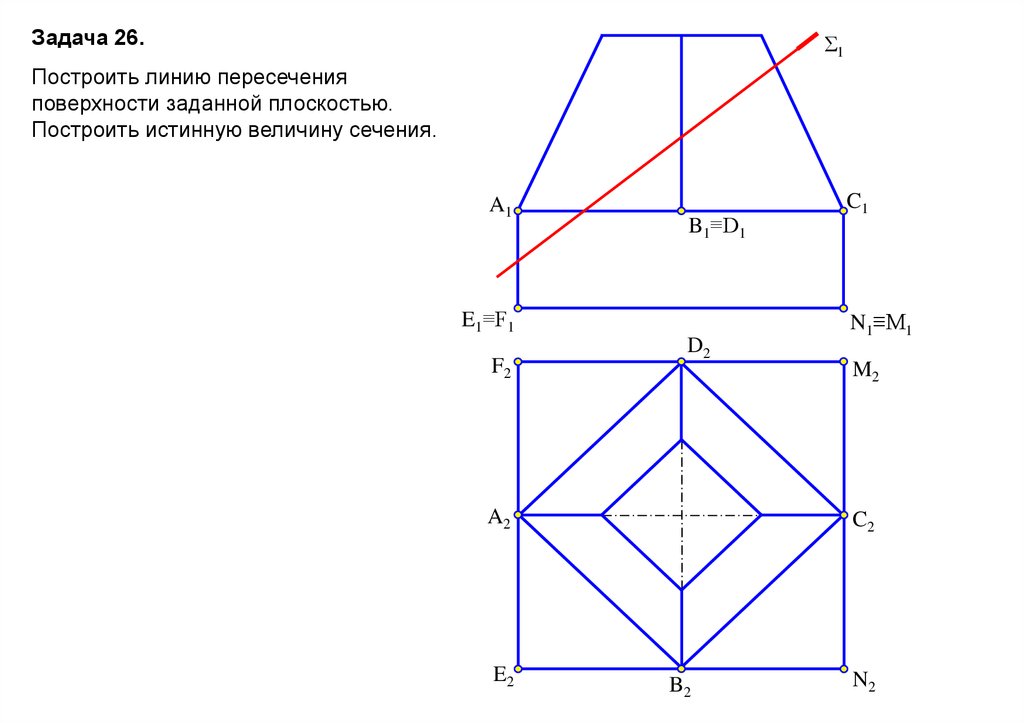
Задача 26.
Σ1
Построить линию пересечения
поверхности заданной плоскостью.
Построить истинную величину сечения.
A1
B1≡D1
E1≡F1
F2
D2
N1≡M1
M2
A2
E2
C1
C2
B2
N2

107.

Задача 27.
53
Σ1
Построить линию пересечения
поверхности заданной плоскостью.
Построить истинную величину
сечения.
A1
B1≡D1
C1
D2
A2
C2
B2

108.

ПРИМЕР ВЫПОЛНЕНИЯ СЕЧЕНИЕ ДЕТАЛИ ПЛОСКОСТЬЮ

109.

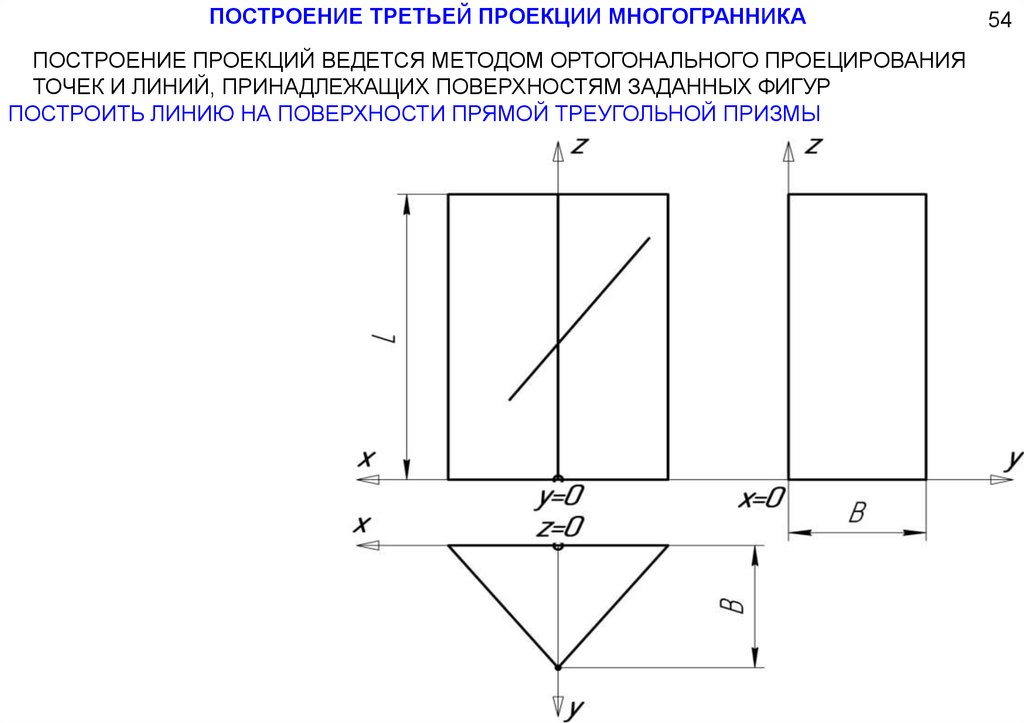
ПОСТРОЕНИЕ ТРЕТЬЕЙ ПРОЕКЦИИ МНОГОГРАННИКА
ПОСТРОЕНИЕ ПРОЕКЦИЙ ВЕДЕТСЯ МЕТОДОМ ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ
ТОЧЕК И ЛИНИЙ, ПРИНАДЛЕЖАЩИХ ПОВЕРХНОСТЯМ ЗАДАННЫХ ФИГУР
ПОСТРОИТЬ ЛИНИЮ НА ПОВЕРХНОСТИ ПРЯМОЙ ТРЕУГОЛЬНОЙ ПРИЗМЫ
54

110.

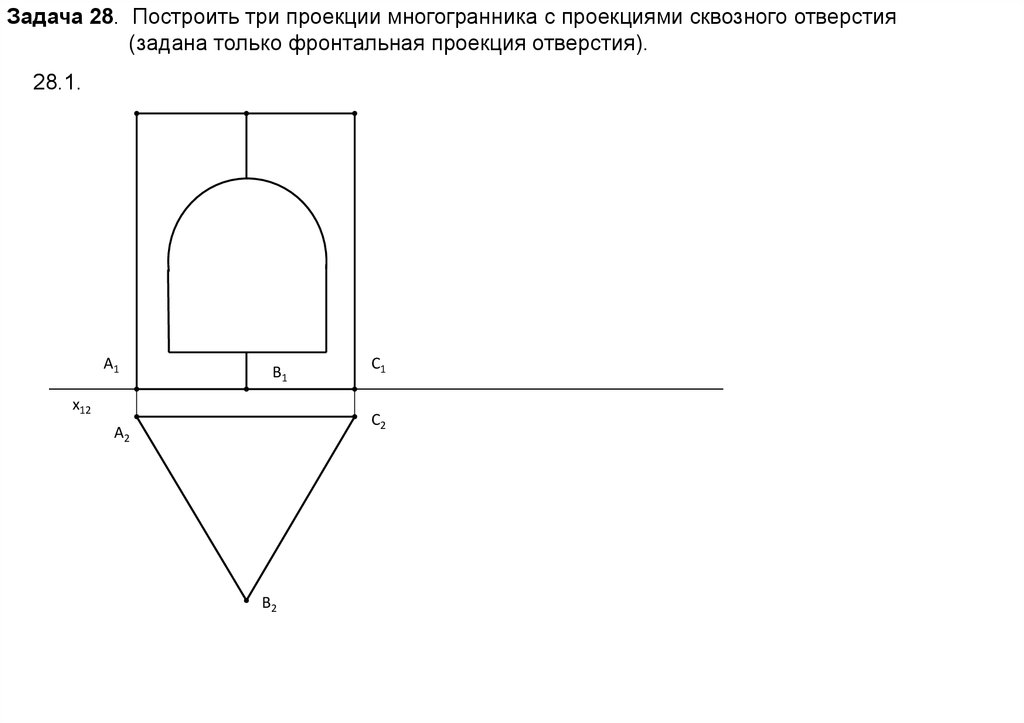
Задача 28. Построить три проекции многогранника с проекциями сквозного отверстия
(задана только фронтальная проекция отверстия).
28.1.
А1
В1
x12
С1
С2
А2
В2

111.

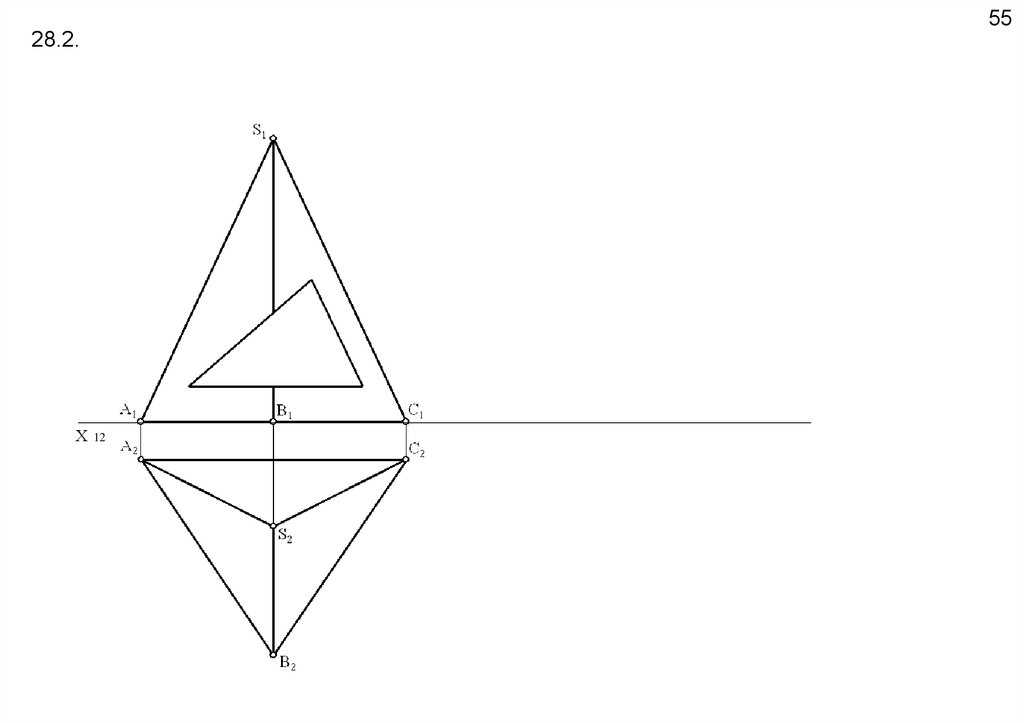
55
28.2.
Х
12

112.

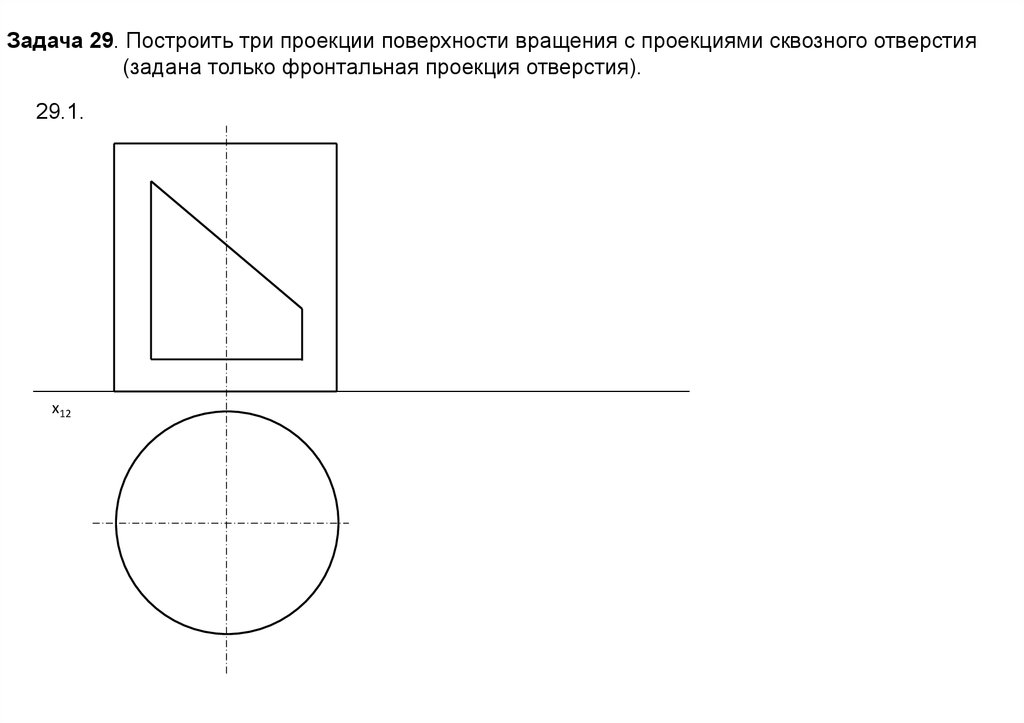
Задача 29. Построить три проекции поверхности вращения с проекциями сквозного отверстия
(задана только фронтальная проекция отверстия).
29.1.
x12

113.

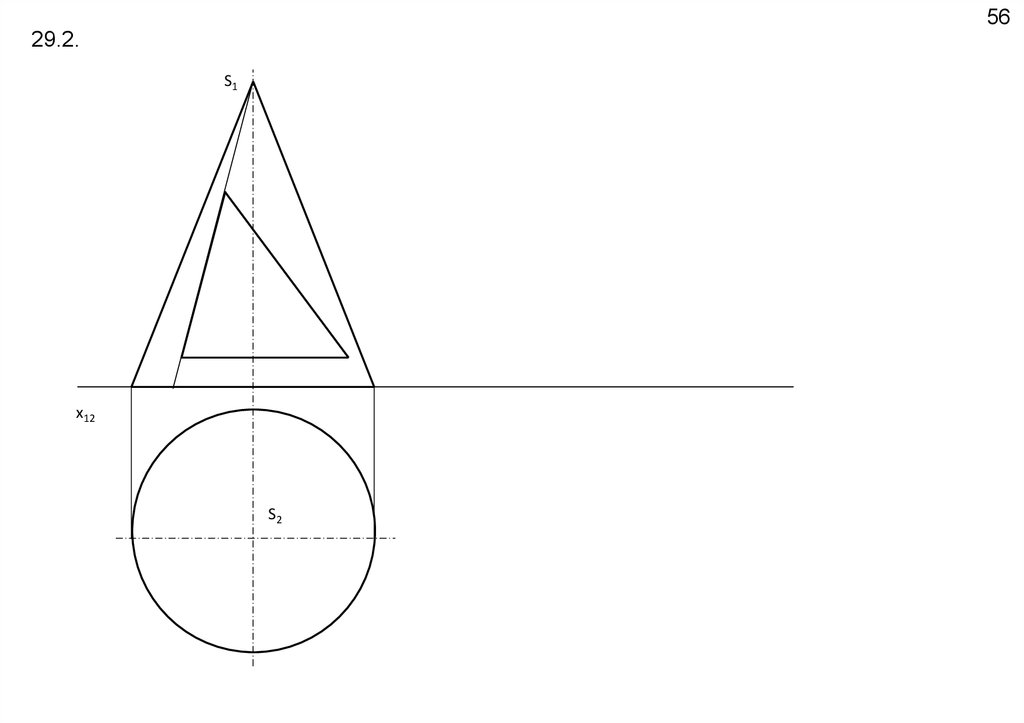
56
29.2.
S1
x12
S2

114.

ПЕРЕСЕЧЕНИЕ ПРЯМОЙ С ПОВЕРХНОСТЬЮ
Алгоритм решения :
l

115.

ПОСТРОЕНИЕ ТОЧЕК ПЕРЕСЕЧЕНИЯ ПРЯМОЙ С ПОВЕРХНОСТЬЮ
Задача 30. Определить точки пересечения прямой с поверхностью пирамиды.
57

116.

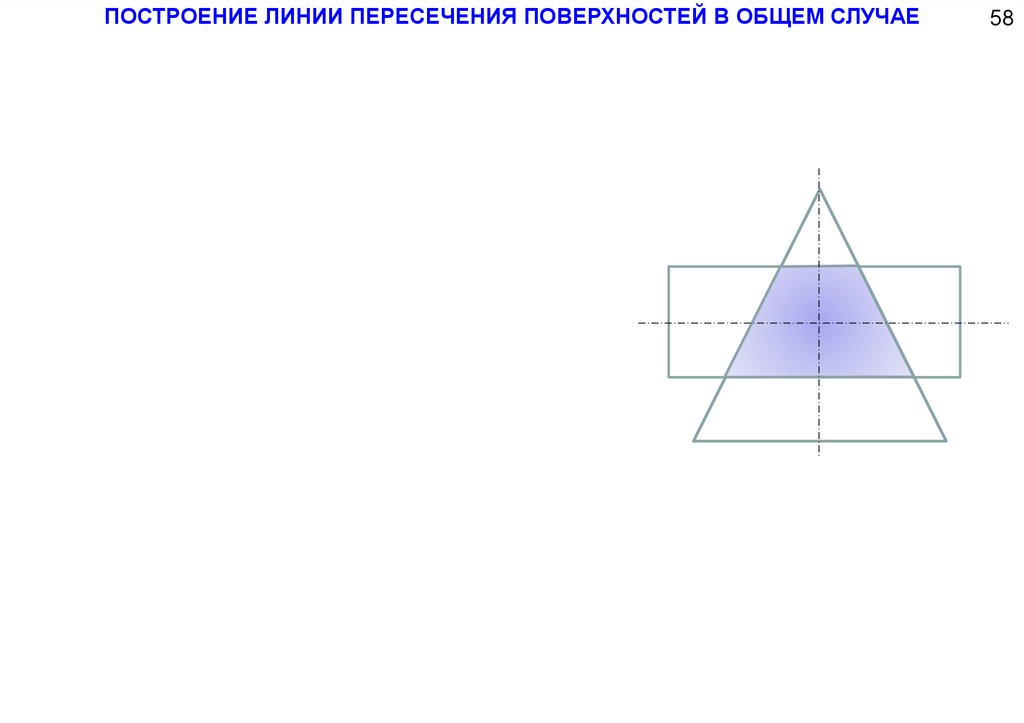
ПОСТРОЕНИЕ ЛИНИИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ В ОБЩЕМ СЛУЧАЕ

117.

ПОСТРОЕНИЕ ЛИНИИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ В ОБЩЕМ СЛУЧАЕ
58

118.

ПОСТРОЕНИЕ ЛИНИИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ СПОСОБОМ
ВСПОМОГАТЕЛЬНЫХ ПЛОСКОСТЕЙ УРОВНЯ

119.

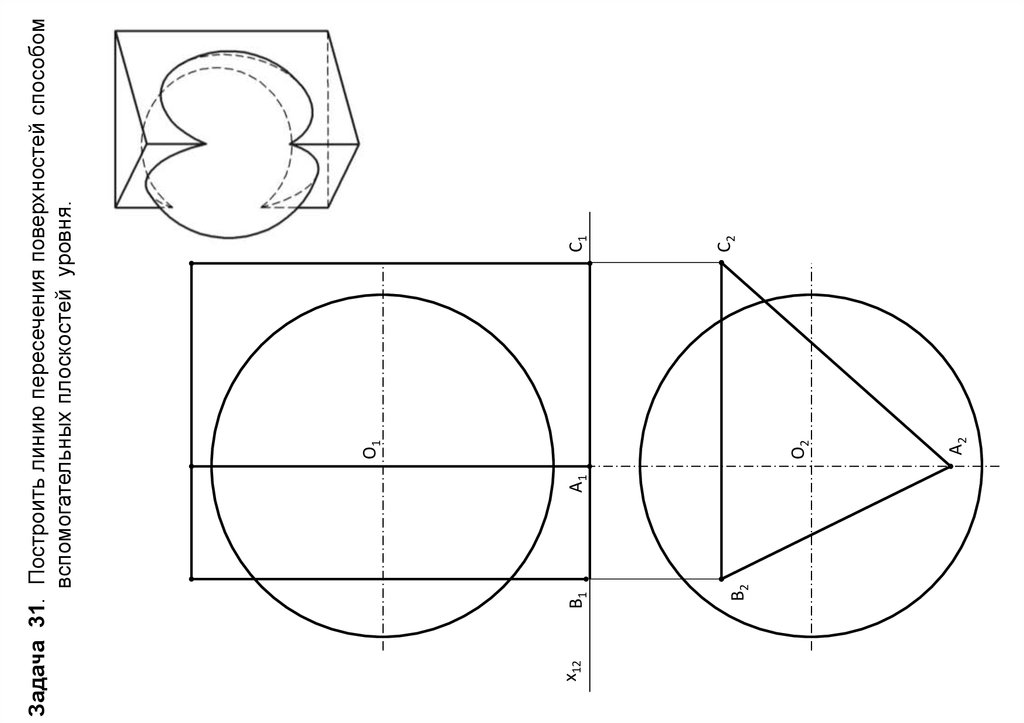
ПОСТРОЕНИЕ ЛИНИИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ ЦИЛИНДРА И СФЕРЫ
МЕТОДОМ СЕКУЩИХ ПЛОСКОСТЕЙ
59

120.

x12
В2
В1
А1
А2
O2
O1
С2
С1
Задача 31. Построить линию пересечения поверхностей способом
вспомогательных плоскостей уровня.

121.

O1
O2
В2
В1
А1
А2
С2
С1
O'2
O'1
Задача 32. Построить линию пересечения поверхностей способом
вспомогательных плоскостей уровня.
60

122.

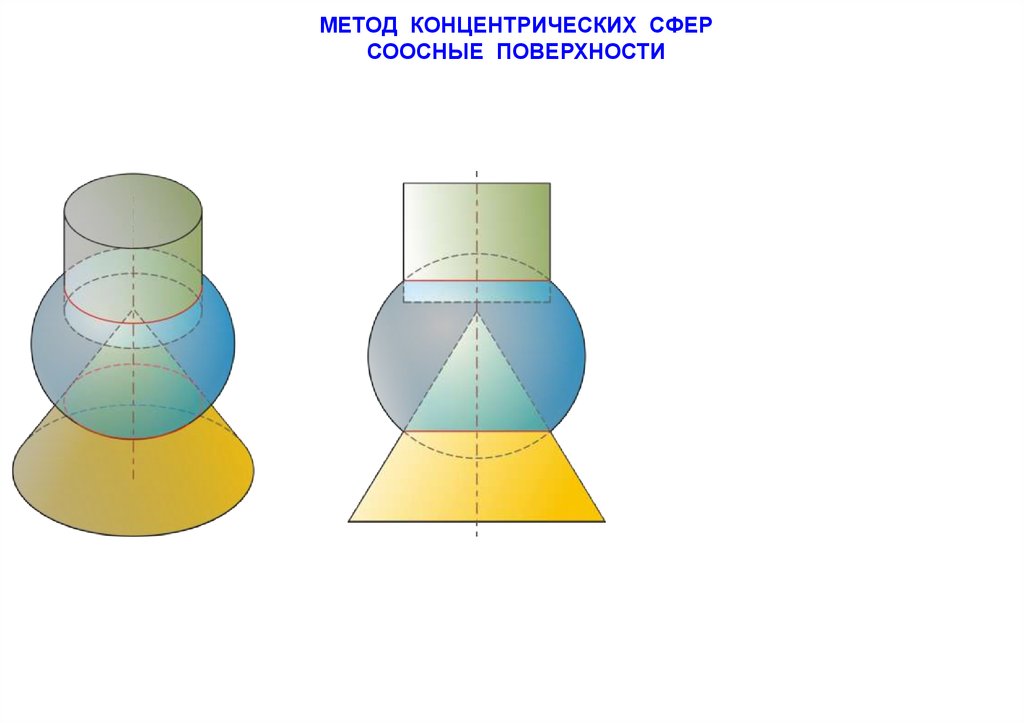
МЕТОД КОНЦЕНТРИЧЕСКИХ СФЕР
СООСНЫЕ ПОВЕРХНОСТИ

123.

МЕТОД КОНЦЕНТРИЧЕСКИХ СФЕР
61

124.

ПОСТРОЕНИЕ ЛИНИИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ МЕТОДОМ
КОНЦЕНТРИЧЕСКИХ СФЕР
О1
Ʃ2
О2

125.

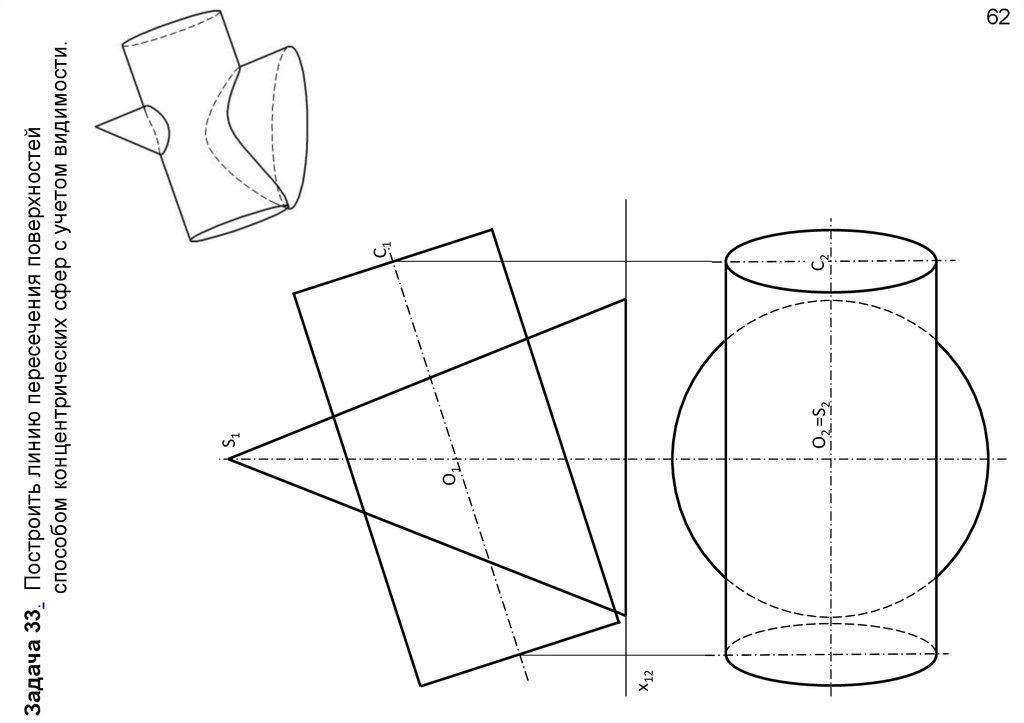
x12
O1
O2 =S2
S1
С2
С1
Задача 33. Построить линию пересечения поверхностей
способом концентрических сфер с учетом видимости.
62

126.

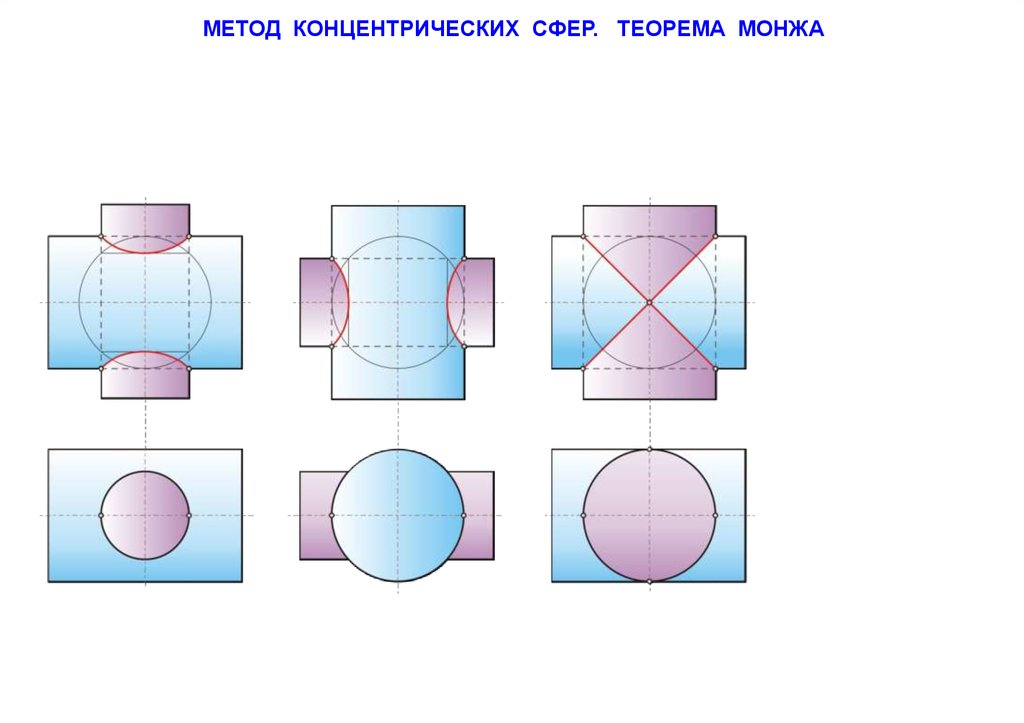
МЕТОД КОНЦЕНТРИЧЕСКИХ СФЕР. ТЕОРЕМА МОНЖА

127.

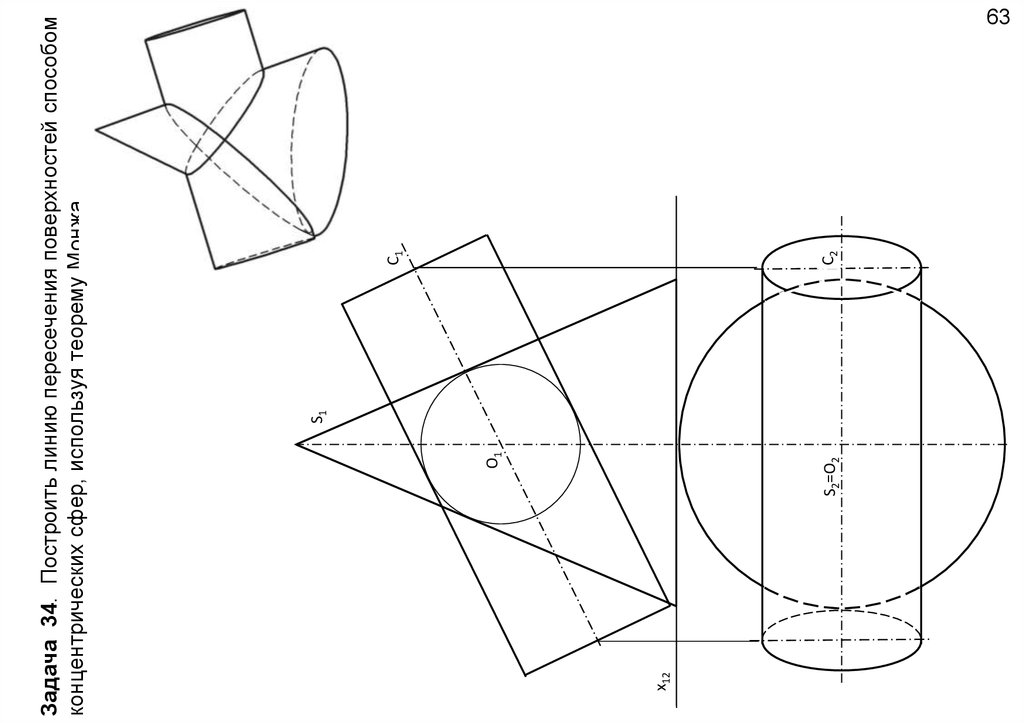
x12
S2=O2
O1
S1
С2
С1
Задача 34. Построить линию пересечения поверхностей способом
концентрических сфер, используя теорему Монжа.
63

128.

ПЕРЕСЕЧЕНИЕ МНОГОГРАННИКОВ
ЛИНИЕЙ ПЕРЕСЕЧЕНИЯ МНОГОГРАННИКОВ

129.

ПОСТРОЕНИЕ ЛИНИИ ПЕРЕСЕЧЕНИЯ МНОГОГРАННИКОВ
64

130.

131.

СПИСОК
ЛИТЕРАТУРЫ
65
1. « Использование ГОСТов в машиностроительном черчении » Н.Е.Зайко, А.Ю.Логинов,
Н.И.Запорожцева. Методические указания. Н.Новгород, ФГОУ ВПО «ВГАВТ» 2006 год.
2. «Изображения : виды, разрезы, сечения» Н.Е.Зайко, И.Н. Шоркина . Учебно-методическое пособие.
Н.Новгород, ФБОУ ВПО «ВГАВТ» 2012 год.
3. «Резьбы и резьбовые соединения» Н.Е. Зайко, С.П. Новиков, С.Н. Уртминцева, И.Н. Шоркина .
Методическое пособие. Н.Новгород, ФБОУ ВПО «ВГАВТ» 2014 год.
4. «Начертательная геометрия» С.В. Тарасова, С.П. Новиков. Методическое пособие. Н.Новгород, ФГОУ
ВПО «ВГАВТ» 2004 год.
5. «Инженерная графика» Н.А. Анисимова, Н.Е. Зайко, С.Н. Уртминцева. Методические указания.
Н.Новгород, ФБОУ ВПО «ВГАВТ» 2014 год.
6. «Расчётно-графические работы по начертательной геометрии» Е.Л. Алексеева, А.Ю. Логинов,
И.Н. Шоркина. Методические указания. Н.Новгород, ФГОУ ВПО «ВГАВТ» 2011 год.
7. «Плоскостное моделирование в графической системе КОМПАС- 3D». Н.И. Анисимова. Методические
указания. Н.Новгород, ФГОУ ВПО «ВГАВТ» 2009 год.

132.

Лекционно-практическая тетрадь по начертательной геометрии и инженерной графике для студентов дневного
отделения (специальностей 26.03.02 - Кораблестроение, 20.03.01 - Техносферная безопасность, 26.03.01- Управление
водным транспортом, 08.03.01- Строительство, 26.05.06 - Эксплуатация судовых энергетических установок, 23.03.03 Эксплуатация транспортно-технологических машин и комплексов)/ Составители Н.А. Анисимова, И.Н. Шоркина.
Кафедра ТКИС – Н. Новгород : ФГБОУ ВО «ВГУВТ», 2018. – 65 с.
Настоящее тетрадь поможет оптимизировать процесс освоения теоретического и практического материала по
начертательной геометрии и инженерной графике.
Тетрадь рекомендована кафедрой теории конструирования инженерных сооружений.
Н.А. Анисимова, И.Н. Шоркина
ЛЕКЦИОННО-ПРАКТИЧЕСКАЯ ТЕТРАДЬ
ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ И ИНЖЕНЕРНОЙ ГРАФИКЕ
Печатается по авторскому оригиналу
без редактирования и корректуры
Усл. печ. 4 л. © ФГБОУ ВО «ВГУВТ», 2018
603950, Нижний Новгород, ул. Нестерова, 5