Похожие презентации:
Кодирование сообщений в отсутствии шума
1.
Кодированиесообщений в
отсутствие шума
2.
Средняя длина кодового словаn
L i P ( xi )
i 1
i
длина кодового слова
3.
log P( xi ) i log m,log P( xi )
i
log m
n
n
P( xi )log P( xi )
i 1
log m
i P( xi )
i 1
4.
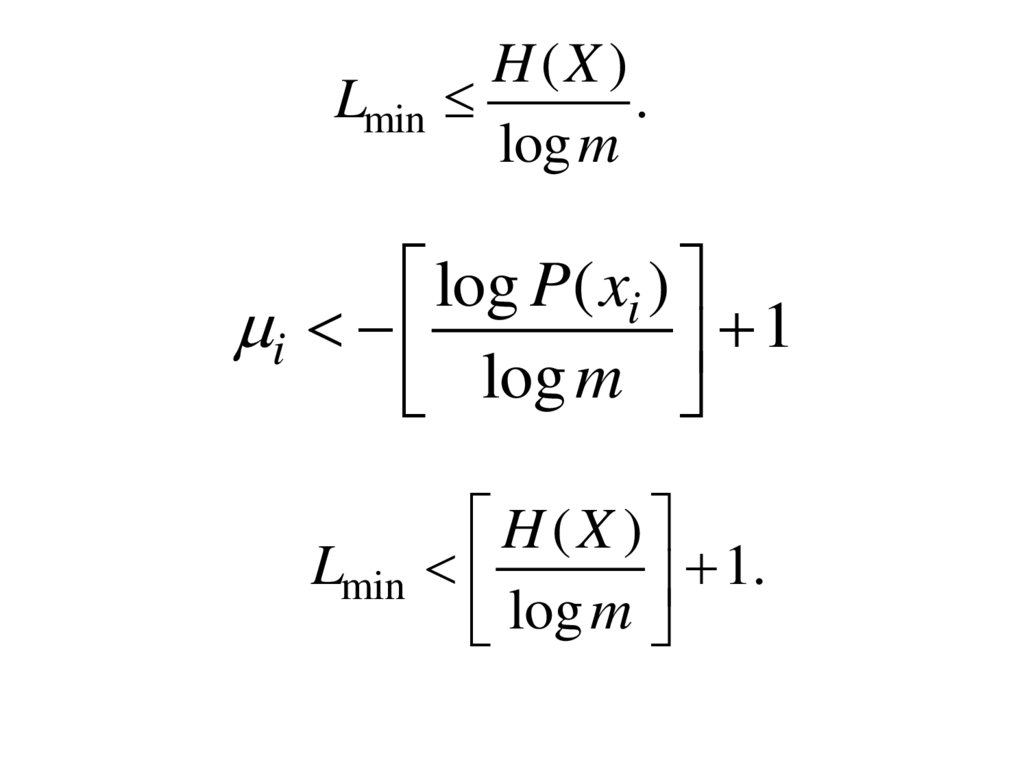
LminH(X )
.
log m
log P( xi )
i
1
log m
Lmin
H (X )
1.
log m
5.
H(X )H(X )
Lmin
1.
log m
log m
Теорема Крафта. Если 1, 2 , , n
– длины кодовых слов, соответствующих
сообщениям х1, х2 , , хn , то необходимым и
достаточным
условием
существования
неперекрываемых кодовых слов с заданными
длинами является выполнение неравенства
n
m
k
1
k 1
m - число различных символов в кодовом алфавите
6.
Теорема Шеннона.При кодировании сообщений х1, х2 ,
, хn
в алфавите насчитывающем m символов,
при условии отсутствия шумов,
средняя длина кодового слова не может
H(X )
быть меньше, чем log m
энтропия сообщений
, где H ( X ) -
7.
ДИСКРЕТНЫЕ КАНАЛЫ С ШУМАМИМодель канала связи при наличии шумов
8.
kk
N m N0 m
N0 N
N0 N
k
N ( N0 N )
N
N0
9.
Пропускная способностьдискретного канала связи с
шумами
10.
I (WT , X T )I (W , X ) lim
(бит/ с)
T
T
С max I (W , X ) (бит/ с)
Сс max I (Z ,Y ) (бит/ с),
I ( ZT , YT )
{Z} {Y}
11.
I ( ZT , YT ) H ( ZT ) H ( ZT / YT )H (YT ) H (YT / ZT )
H(Z) – априорная (безусловная)
энтропия ансамбля {Z}
энтропия ансамбля {Z},
H ( ZT / YT ) оставшаяся после
получения сообщения об
ансамбле {Y}
12.
H ( ZT ) МH ( Z ),H ( ZT / YT ) МH ( Z / Y )
I ( ZT , YT ) МH ( Z ) МH ( Z / Y )
МH (Y ) МH (Y / Z )
13.
Теоремы окодировании в
присутствие шумов
14.
Теорема 1 (К. Шеннон). Если потокинформации H ( X ) создаваемый
источником
H ( X ) Сс
где может быть сколь угодно малым
положительным числом, то существует
такой код, при котором вероятность
ошибок на приемном конце сколь
угодно мала; Сс – пропускная
способность линии связи.
15.
Теорема 2 (К. Шеннон). Если потокинформации создаваемый источником
H ( X ) Сс ,
где 0 , то среди кодов,
обеспечивающих
сколь угодно малую вероятность ошибки,
существует код, при котором скорость
передачи информации I Сс
16.
Теорема 3 (К. Шеннон). Если потокинформации создаваемый источником
H ( X ) Сс
где
0
то никакой код не может сделать
вероятность ошибки сколь угодно малой
Минимальные потери информации в
единицу времени [ H ( X / Y )] равны
17.
Фундаментальноесвойство энтропии
дискретных
эргодических
источников
18.
Теорема 1. Для любых ε>0 и δ>0 можнонайти такое М0, при котором эргодические
последовательности С длиной М M 0
распадаются на два класса: 1) нетипичные,
сумма вероятностей которых меньше ε;
2)
типичные,
вероятности
которых
удовлетворяют следующему неравенству:
1
log
P (С )
H (X )
,
M
19.
Следствие 1. Типичныепоследовательности приблизительно
равновероятны и число их равно
NТ 2
M Н (Х)
Следствие 2. При больших М множество
типичных последовательностей
охватывает малую долю всех возможных
последовательностей, вырабатываемых
эргодическим источником.
20.
N nM
2
log n М
2
M log n
Следствие 3. Чтобы экспериментально
определить энтропию эргодического
источника, у которого вероятностные связи
распространяются на очень большое число
символов, нам необходимо располагать
последовательностью еще большей длины М
при этом вычисленная энтропия будет
близка к своему пределу
1
log
Н(Х )
P(С )
21.
Пример 1. Эргодический источник сэнтропией Н ( Х ) 1,9 (бит) вырабатывает
четыре различных символа. Найти
отношение числа типичных к общему числу
всевозможных последовательностей длиной
М 100 (символов).
Решение. Число типичных
последовательностей
NТ 2
M Н (Х)
100 1,9
190
2
2
M
100
200
а всех возможных N n 4
2
22.
190NТ 2
1
1
200 10
0,001
N 2
1024
2
Таким образом, типичные составляют
одну
тысячную
всех
возможных
последовательностей.
23.
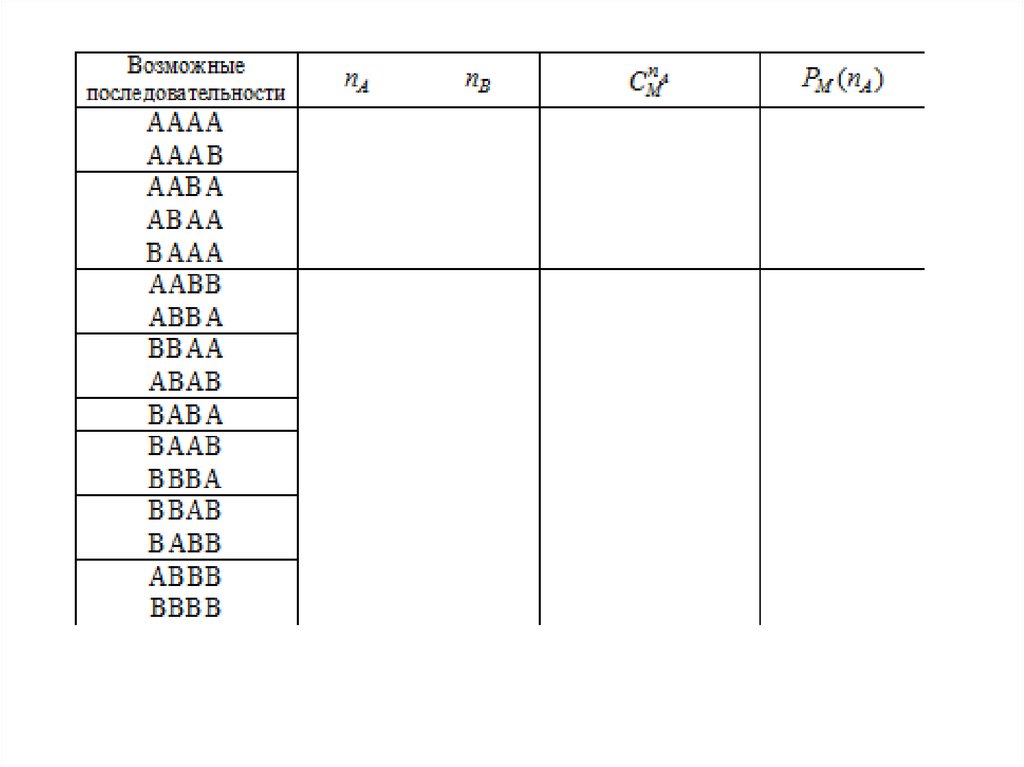
Пример 2. Источник вырабатывает с одинаковойвероятностью два символа А и В. Определить
количество возможных последовательностей,
содержащих n A символов А, причем n A nB M
Определить вероятность события, что в
выработанной источником последовательности
длиной М содержится n A символов А.
M
N 2
nA
СM
M!
.
nA !( M n A )!
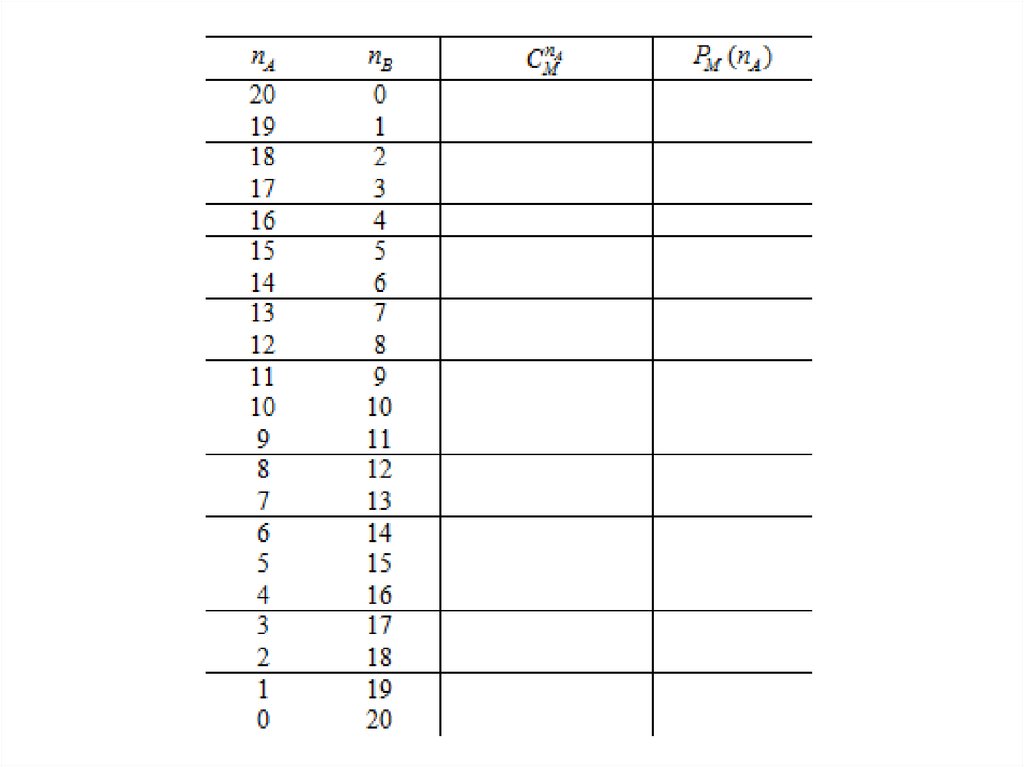
24.
nAPМ (n A ) CM
p
nA
q
M nA
nA
CM
P( B) q 1/ 2
P( А) p 1/ 2
I случай. Пусть M 4
N 2
1
2
М
2 16
4
M
25.
26.
II случай. Пусть M 20N 2
М
2
20
1048476


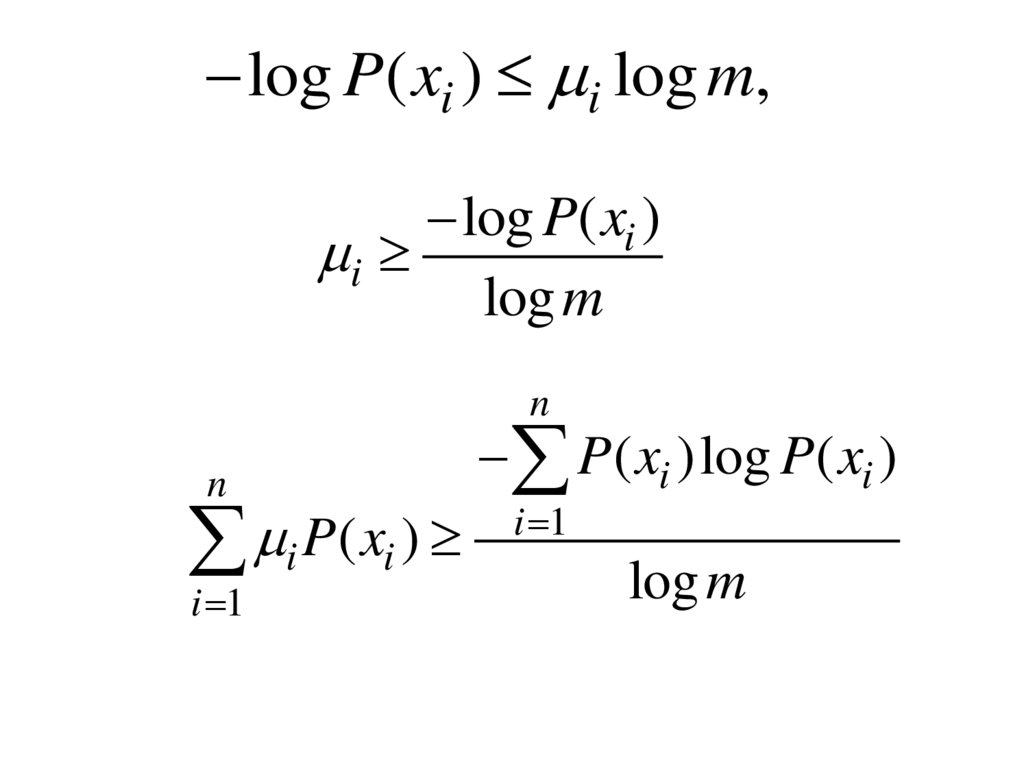



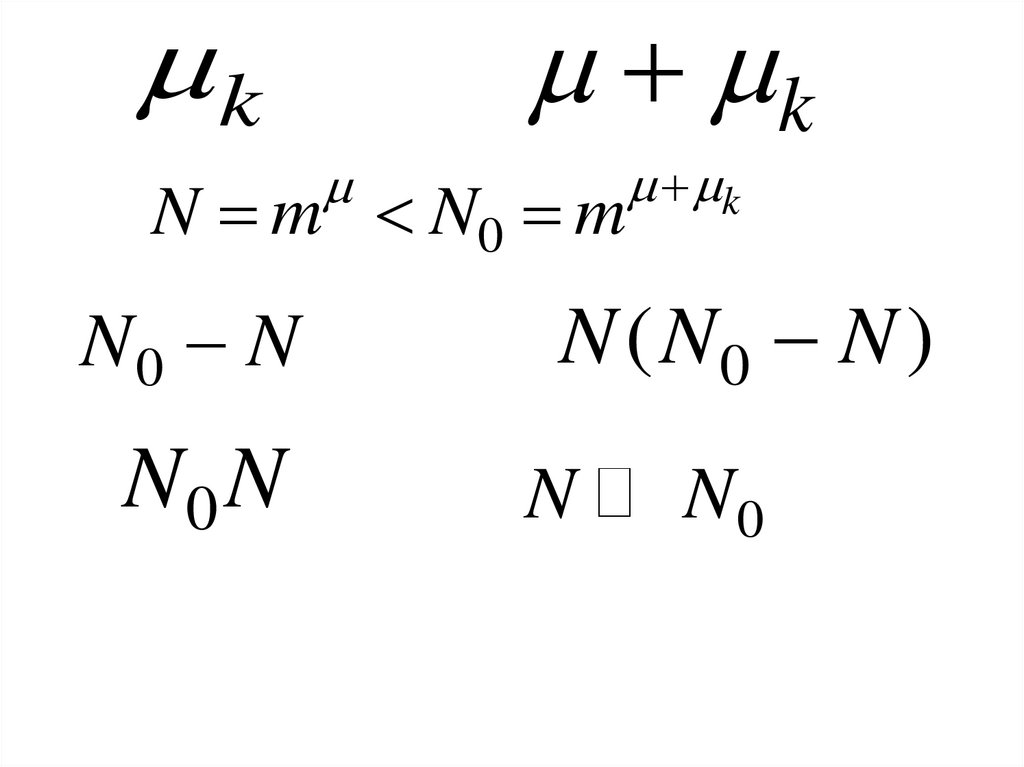

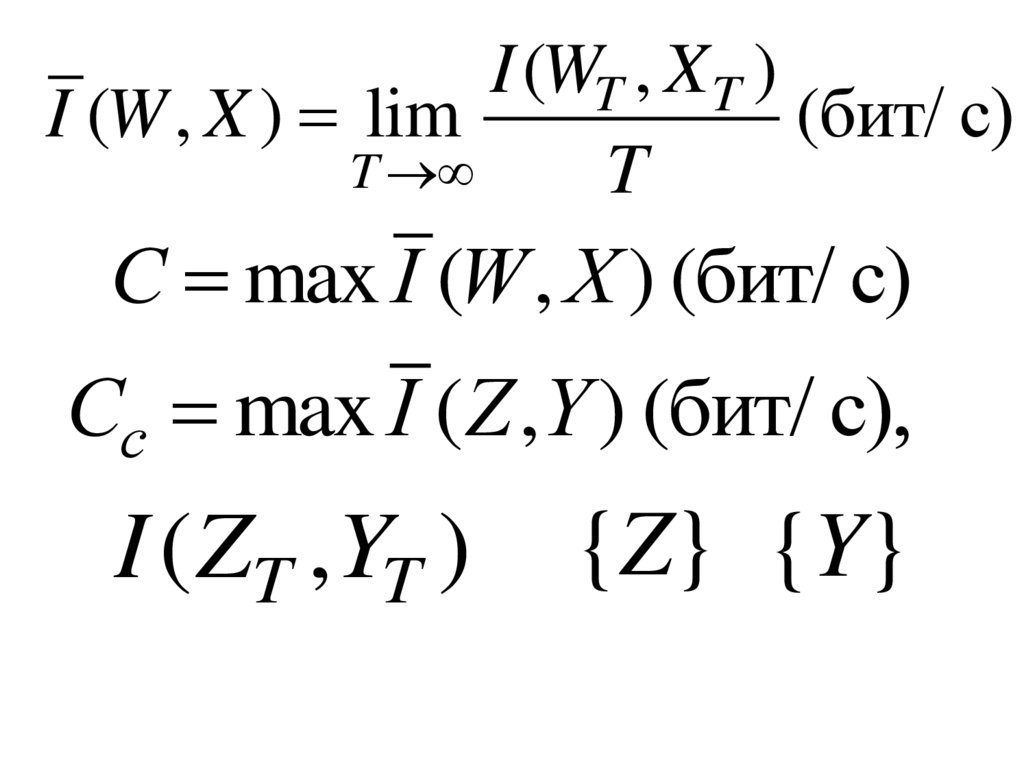

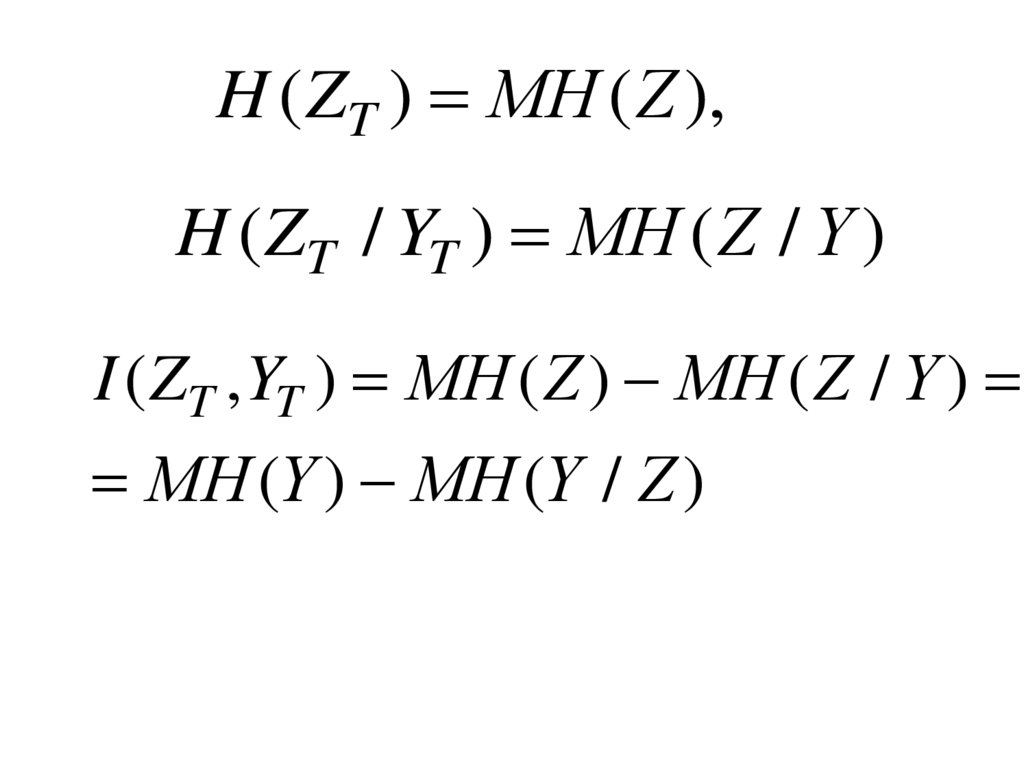











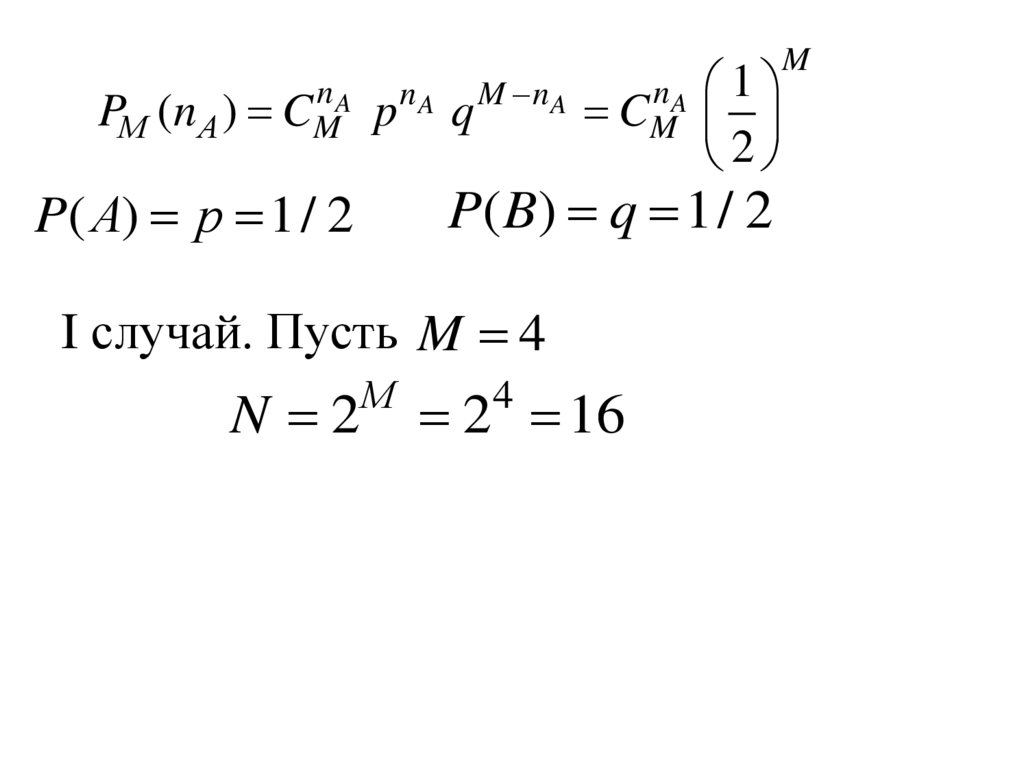
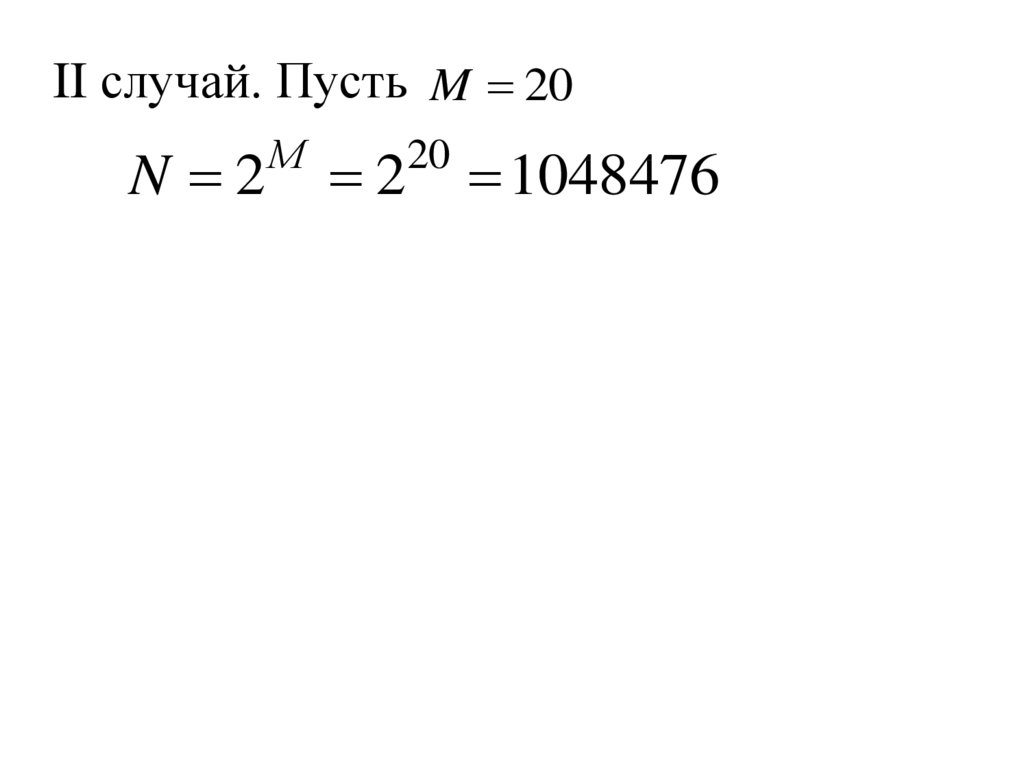
 Математика
Математика Физика
Физика








