Похожие презентации:
Математические основы манипулирования реляционными данными
1.
Математические основы манипулированияреляционными данными
2.
Запрос - это операция над отношениями,приводящая к построению результирующих
отношений.
Языки запросов могут быть построены:
1)на основе операторов реляционной алгебры,
2)на основе систем реляционного исчисления.
3.
1. РЕЛЯЦИОННАЯ АЛГЕБРАΨ ={A, D, J, P, R, Θ, X}
Ψ – реляционная алгебра.
А – множество всех атрибутов предметной области (универсальная
схема отношений).
D – множество доменов.
J – функция из A в D (A→D), определяющая разнесение атрибутов
из A по доменам из D.
P – множество схем отношений, т.е. выделение заголовков столбцов
реляционных таблиц.
R – множество всех экземпляров различных таблиц.
Θ – совокупность операций над доменами из D (>, <, =, и т.д.).
X – операции над экземплярами таблиц (объединение, пересечение,
разность и т.д.).
4.
Реляционная алгебра – это теоретический языкопераций, который на основе одного или нескольких
отношений позволяет создавать другие отношения, без
изменения самих исходных отношений.
Реляционная алгебра является языком
последовательного использования отношений,
в котором все картежи, возможно даже взятые
из разных отношений, обрабатываются одной
командой без применения циклов.
5.
К основным операциям реляционной алгебрыотносятся:
• объединение,
• разность,
• выборка,
• декартово произведение,
• проекция.
К дополнительным относятся –
• пересечение,
• соединение,
• деление.
6.
1. ОбъединениеПусть R – схема отношения r1, r2 – экземпляры отношений со
схемой R.
Объединением отношений r1 и r2 называется отношение r3= r1
r2, каждый кортеж которого принадлежит отношению
r1 или r2.
R A1 , A2
A1
r1 2
A2
5
7
9
A1
1
r2
4
A2
3
6
8
4
r3 r1 r2
A1
A2
2
5
7
9
1
3
4
6
8
4
7.
2. РазностьПусть R – схема отношения r1, r2 – экземпляры отношений со
схемой R.
Разностью отношений r1 и r2 называется отношение r3= r1 – r2,
каждый кортеж которого принадлежит отношению r1, но не
принадлежит отношению r2.
R A1 , A2
A1
r1 2
A2
5
A1
r2 7
A2
9
7
9
3
8
r3 r1 r2
A1
A2
2
5
8.
3. Выборка (селекция)Операция выборки работает только с одной одним отношением
r и определяет результирующее отношение, которое содержит
только те кортежи исходного отношения r, которые удовлетворяют
заданному условию F.
R A1 , A2
r
F A1 A2
A1
A2
2
5
7
9
1
3
t F r 7
1
4
6
4
8
4
A1
2
A2
5
9
3
6
9.
4. Декартово произведениеПусть R, S – схемы отношений со степенями K1, K2, r и s –
экземпляры отношений.
Декартовым произведением t = r s называется отношение со
степенью K1 + K2, кортежи которого получаются путем
конкатенации кортежей из отношения r и s.
R A1 , A2 S A3 , A4 , A5
A1
r 2
7
A2
5
9
A3
8
s
7
2
A4
1
5
4
A5
0
3
6
A1
A2
A3
A4
A5
2
5
8
1
0
2
5
7
5
3
t r s 2
5
2
4
6
7
9
8
1
0
7
9
7
5
3
7
9
2
4
6
10.
5. ПроекцияПроекцией отношения r на множество атрибутов A1, A2,…, An
называется отношение,
t
(r )
A1 , An из значений A , A ,…, A
каждый кортеж которого состоит
1
2
n
отношения r.
A1
8
r
7
2
A2
1
5
4
A3
0
3
6
A1
8
t A1 A3 r
7
2
A3
0
3
6
11.
6. СоединениеΘ – арифметический оператор сравнения,
n – степень отношения r ,
m – степень отношения s,
i, j –атрибуты (номера столбцов) отношений r и s соответственно.
Соединением t отношений r и s называется множество всех
кортежей
таких, что это множество является
соединением какого-либо кортежа из r и какого-либо кортежа из s с
t выражение
r s iΘj истинно.
условием, что
i j
12.
1) Тета-соединениеЕсли Θ – арифметический оператор сравнения, то операция
называется тета-соединением.
A1
r 2
A2
5
3
9
A3
8
s
7
2
A4
1
5
4
A5
0
3
6
A1
2
A2
5
A3
8
A4
1
A5
0
t r s 2
A1 A3
3
5
9
7
8
5
1
3
0
3
9
7
5
3
13.
2) Эквисоединение.Если Θ – арифметический оператор равенства, то операция
называется эквисоединением.
R A1 , A2
A1
r 2
A2
5
7
4
S A3 , A4 , A5
A3
8
s
7
2
A4
1
5
4
A5
0
3
6
A1
t r s 2
A2
5
A3
7
A4
5
A5
3
7
4
2
4
6
A2 A4
14.
3) Естественное соединение.Если присутствуют хотя бы два равных атрибута и один из них
исключается, то результат называют естественным соединением.
R A1 , A2 S A2 , A3 , A4
A3
8
9
1
A4
0
3
6
A1
t r s 2
A2
5
A3
9
A4
3
7
4
1
6
A1
r 2
A2
5
7
4
A2
1
s
5
4
15.
4) Композиция.Это соединение отличается от естественного тем, что из
результирующего отношения удаляют оба атрибута соединения.
R A1 , A2
A1
r 2
A2
5
7
4
S A2 , A3 , A4
A2
1
s
5
4
A1
t r s 2
A3
9
A4
3
7
1
6
A3
8
9
1
A4
0
3
6
16.
7. ПересечениеПусть R – схема отношения r1, r2 – экземпляры отношений со
схемой R.
Результатом операции пересечения двух отношений r1 и r2
является отношение r3= r1 r2, включающее все кортежи, входящие
в оба отношения операнда.
R A1 , A2
A1
r1 2
A2
5
7
9
A1
1
r2
4
A2
3
6
7
9
r3 r1 r2
A1
A2
7
9
17.
8. ДелениеПусть отношение r определено на множестве атрибутов A, а отношение s – на
B, причем B
A,
C = A – B (разность).
Пусть C является множеством атрибутов отношения r, которые не являются
атрибутами отношения s.
Результатом операции деления является набор кортежей отношения r,
определенных на множестве атрибутов C, которые соответствуют комбинации
всех кортежей отношения s.
18.
A12
A2
7
3
2
r
8
5
9
4
6
2
8
1
4
7
A2
s 7
A1
t r/s 2
4
8
19.
пr
л
о
в
э ф
я
м
в
к
о
в
п
л
я
м
в
к
я
м
п
л
к
в
s
t r/s ?
я
м
о
в
20.
t r/sп л
в к
21.
2. СИСТЕМЫ РЕЛЯЦИОННОГО ИСЧИСЛЕНИЯСистемы реляционного исчисления делятся на:
1) системы исчисления с переменными кортежами,
2) система исчисления с переменными на доменах.
22.
2.1. Системы исчисления с переменными кортежамиЗапрос определяет множество кортежей отношения {t:f(t)}, для
которых логическое условие поиска f(t) принимает истинное
значение.
Переменными кортежами являются такие переменные,
областью определения которых является указанное отношение, т. е.
переменные для которых допустимыми значениями могут быть
только кортежи данного отношения.
{t | R1(t) R2(t)}
23.
Атомы формул могут быть:1) R(t),
2) s[i]Өu[j],
3) s[i]Өa или aӨs[i], где a – константа.
Вхождение переменной t в формулу f связано,
если в f оно находится в подформуле,
начинающейся квантором или , за которым
непосредственно следует переменная t.
x R x, y y U x, y, z Q x, y x r U x, y, r x F x
24.
Правильно построенные формулы определяютсярекурсивно следующим образом:
1. Каждый атом – это формула.
2. Если φ1 и φ2 - формулы, то выражения φ1 φ2,
φ1 φ2, ¬φ1, также являются формулами.
3. Если φ – формула, то (s)(φ) – также формула.
4. Если φ – формула, то (s)(φ) - также формула.
5. Формулы могут заключаться в скобки.
6. Используется следующий порядок старшинства:
- арифметические операторы сравнения;
- кванторы;
- , , ¬.
25.
2.2. Система исчисления с переменными надоменах
Запрос определяет
{x1, x2, …, xn: f(x1, x2, …, xn)} – множество значений x1, x2, …, xn –
из доменов, для которых логическое условие поиска f(x1, x2, …, xn)
принимает истинное значение.
Выражение R(x,y) является истинным, тогда и только тогда,
когда в отношении R имеется кортеж со значениями x и y в двух его
атрибутах.
26.
Атомы формул могут быть:1. R(x1x2…xk), где R - k-арное отношение; xi константа или переменная на некотором домене.
2. х
y, где x и y – константы или переменные на
некотором домене, Ө –оператор сравнения.
27.
3. ОПРЕДЕЛЕНИЕ РЕЛЯЦИОННОЙПОЛНОТЫ
Пусть реляционная база данных содержит множество отношений
R{R1, R2, …, Rп}, а множество C(R) представляет собой множество
отношений, полученных из R с помощью операций реляционной
алгебры.
Язык обладает реляционной полнотой, если он может охватить
все связи, представленные C(R).
28.
Для обеспечения реляционной полноты приреализации языка необходимы две следующие
операции:
1) операция присваивания, т.е. возможность
создавать новые отношения для хранения
результатов операций реляционной алгебры,
являющихся также отношениями.
2) операция транзитивного замыкания,
допускающая рекурсию или вложенность
операций реляционной алгебры для построения
выражений произвольной сложности.

















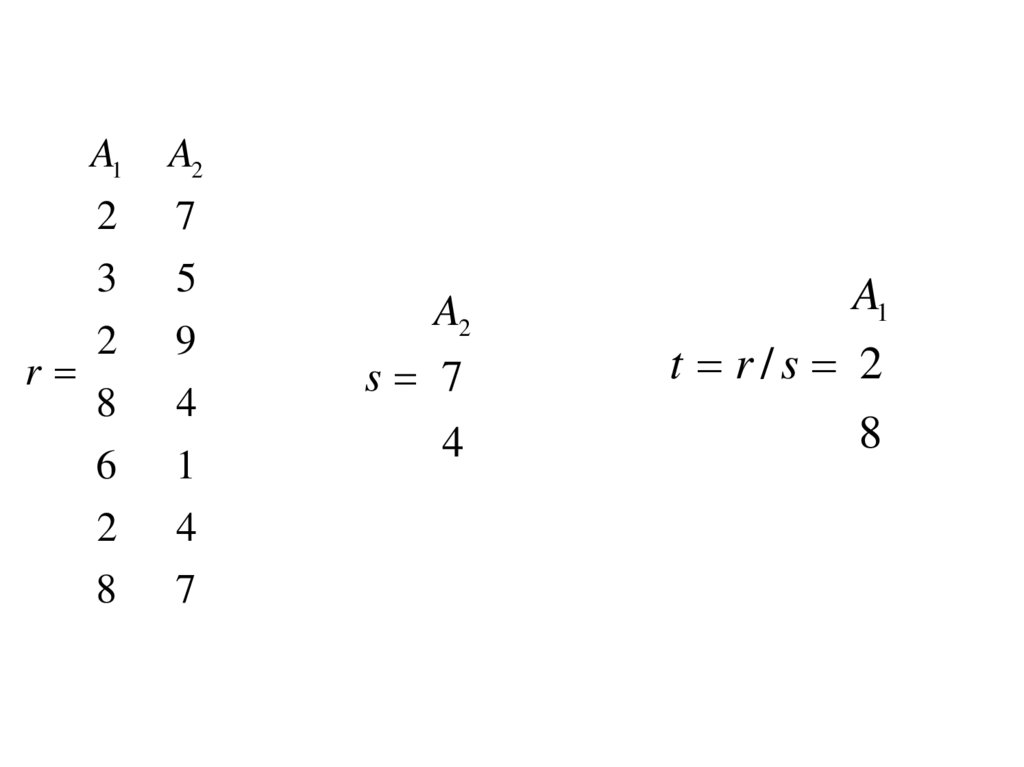










 Математика
Математика