Похожие презентации:
Вектора в пространстве. Система координат в пространстве
1. ВЕКТОРА В ПРОСТРАНСТВЕ
ГЕОМЕТРИЯ 11 КЛАСС2. Система координат в пространстве
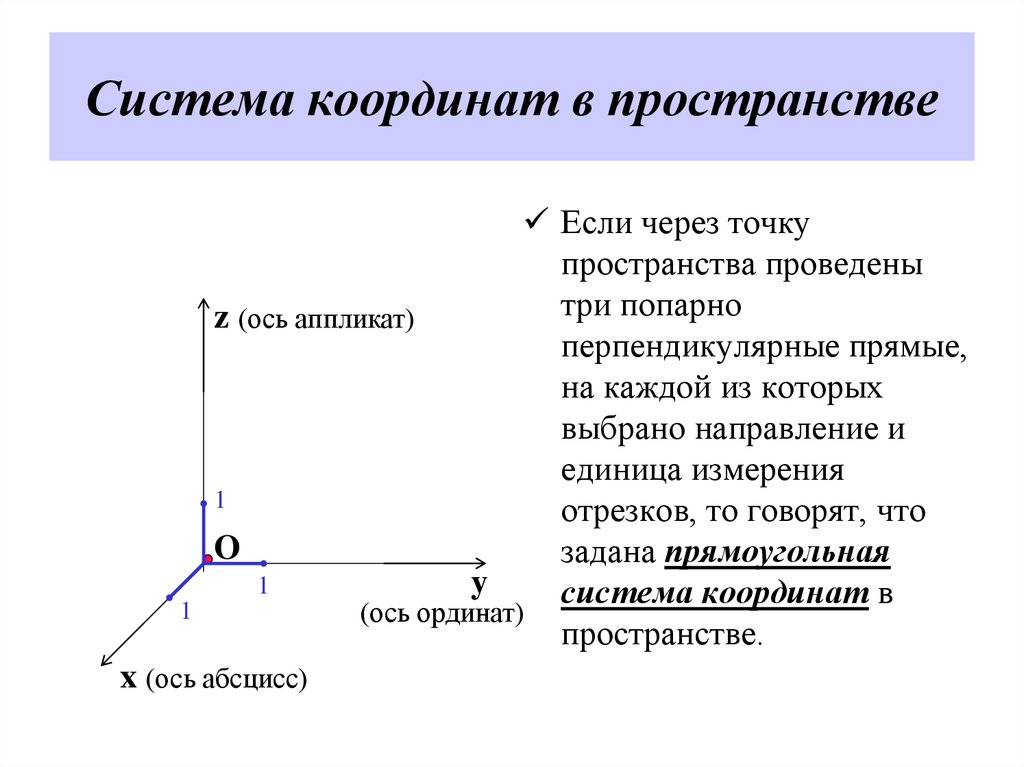
1Если через точку
пространства проведены
три попарно
z (ось аппликат)
перпендикулярные прямые,
на каждой из которых
выбрано направление и
единица измерения
1
отрезков, то говорят, что
O
задана прямоугольная
y
1
система координат в
(ось ординат)
пространстве.
x (ось абсцисс)
3. Система координат в пространстве
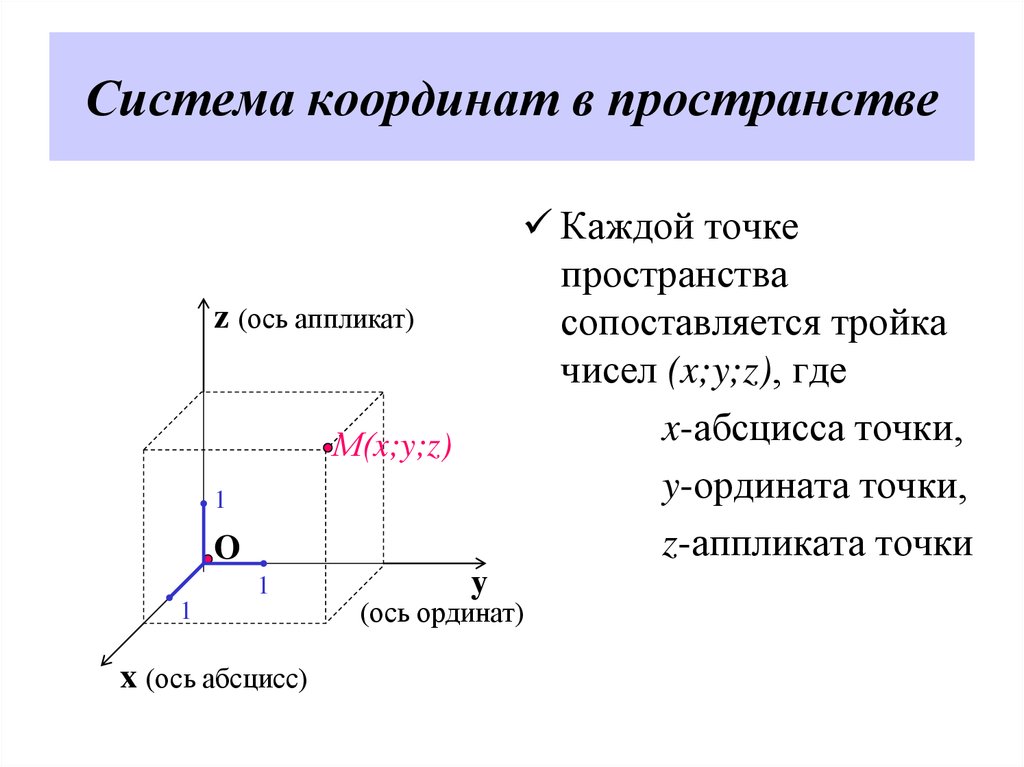
Каждой точкепространства
сопоставляется тройка
чисел (x;y;z), где
x-абсцисса точки,
y-ордината точки,
z-аппликата точки
z (ось аппликат)
М(x;y;z)
1
O
1
1
x (ось абсцисс)
y
(ось ординат)
4. Система координат в пространстве
zM3(0 ; y ; z)
Если точка лежит в
плоскости Oxy, то она
имеет координатыМ1(x ; y ; 0)
M2(x ; 0 ; z)
M(x ; y ; z)
В Охz - М2(x ; 0; z)
O(0;0;0)
y
M1(x ; y ;0)
x
В Oyz - М3(0 ; y ; z)
5. Система координат в пространстве
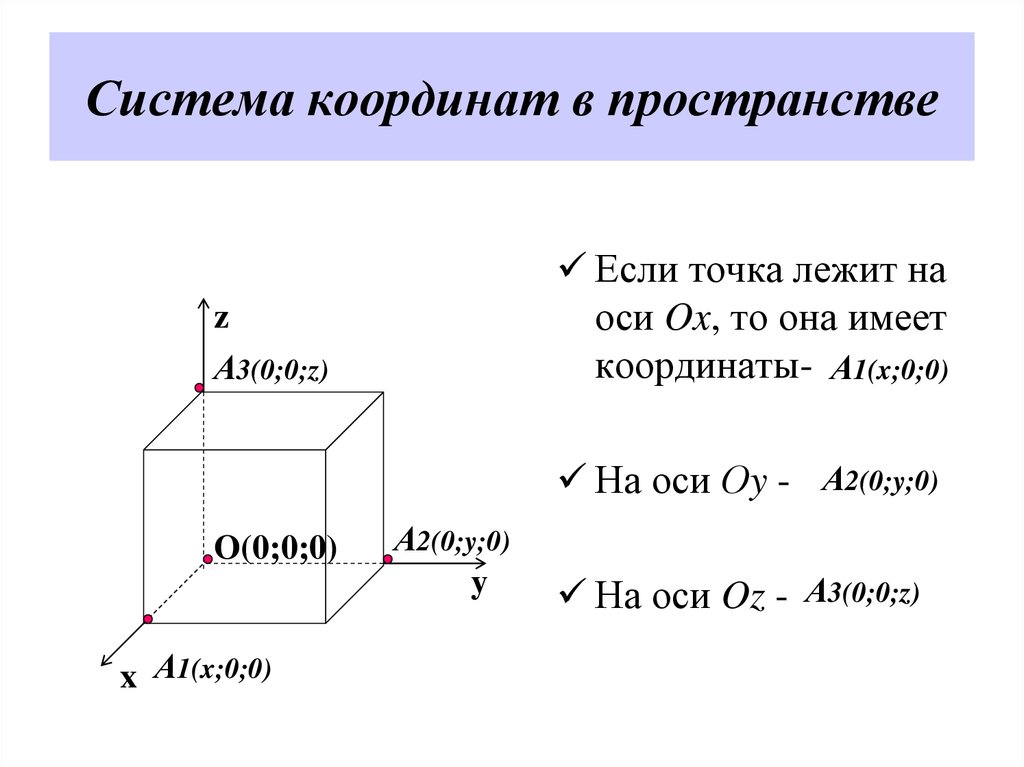
Если точка лежит наоси Ox, то она имеет
координаты- А1(x;0;0)
z
А3(0;0;z)
На оси Оy - А2(0;y;0)
O(0;0;0)
x А1(x;0;0)
А2(0;y;0)
y
На оси Oz - А3(0;0;z)
6. Система координат в пространстве
Вектора ⃗i , ⃗j и ⃗kназываются единичными
координатными
векторами
z (ось аппликат)
⃗
⃗
⃗
• i ‖ Ox , j ‖ Oy , k ‖ Oz
⃗k
• | ⃗i | = | ⃗j | = ⃗| k | = 1
O
⃗i
⃗j
x (ось абсцисс)
y
(ось ординат)
⃗ ⃗ ⃗ ⃗ ⃗ ⃗
• i⊥j ; j⊥k ; i⊥k
7. Связь между координатами векторов и координатами точки
Вектор конец которогосовпадает с данной точкой, а
начало с началом координат
называется радиус-вектором
z
А(а1;а2;а3)
⃗ 1;а2;а3)
ОА(а
Координаты любой точки
равны соответствующим
координатам радиус-вектора
⃗k
O
⃗i
x
⃗j
y
8. Связь между координатами векторов и координатами точки
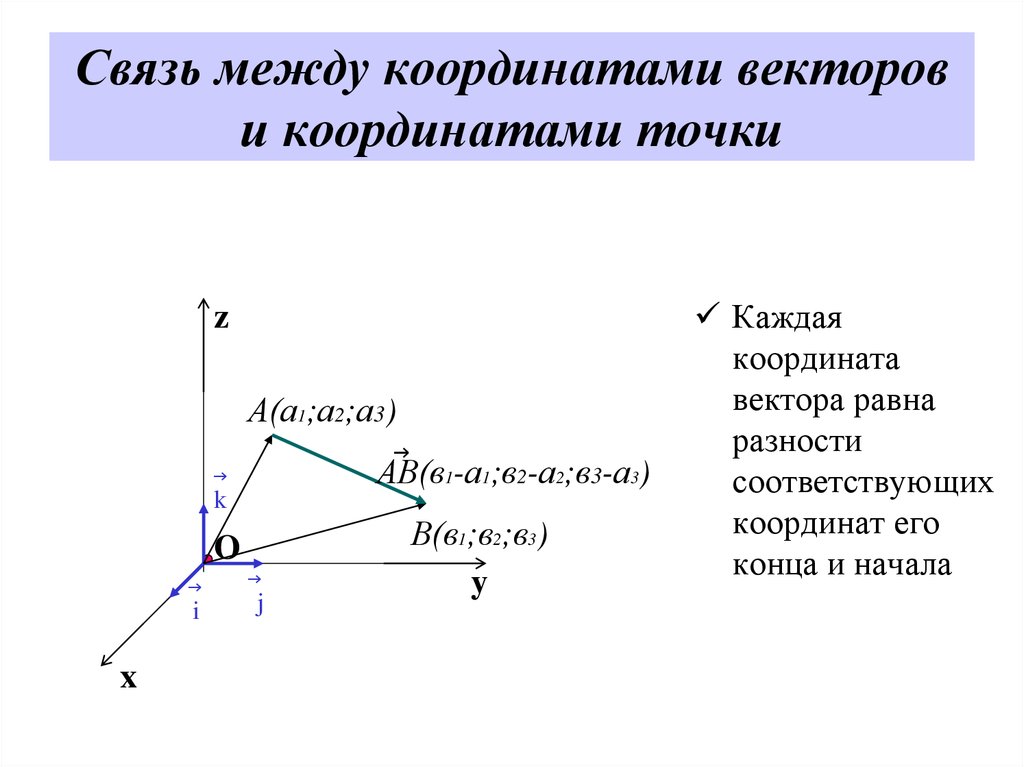
zА(а1;а2;а3)
⃗ 1-а1;в2-а2;в3-а3)
АВ(в
⃗k
O
⃗i
x
⃗j
В(в1;в2;в3)
y
Каждая
координата
вектора равна
разности
соответствующих
координат его
конца и начала




 Математика
Математика








