Похожие презентации:
Декартова система координат в пространстве
1. Декартова система координат в пространстве
2.
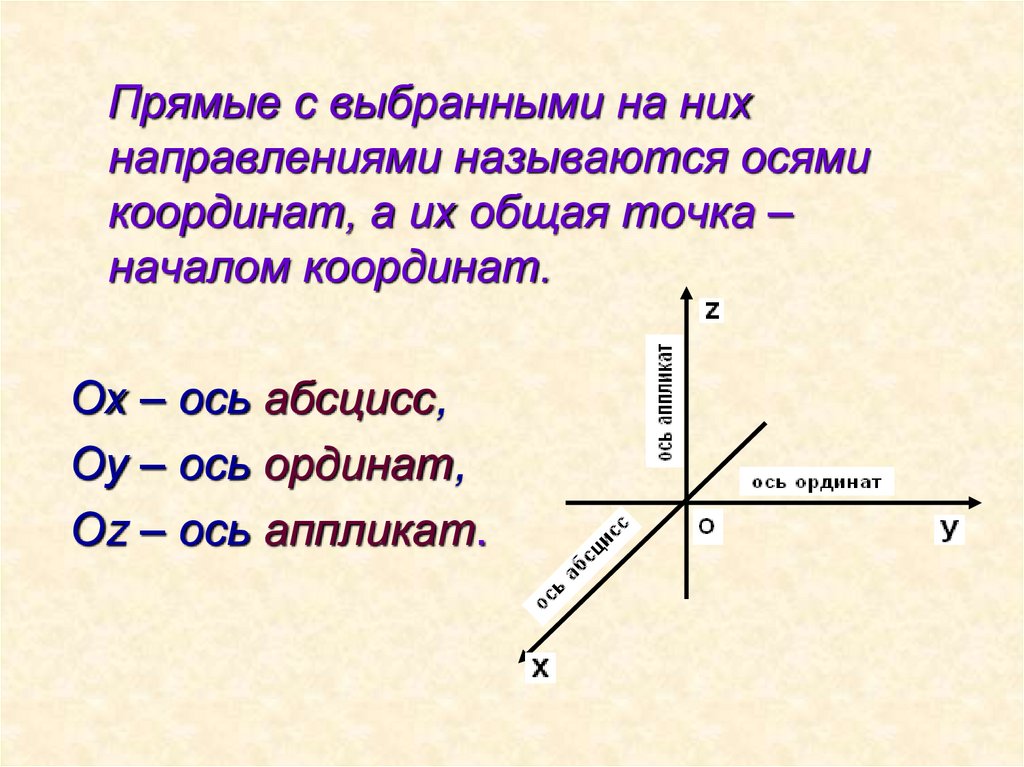
Прямые с выбранными на нихнаправлениями называются осями
координат, а их общая точка –
началом координат.
Ох – ось абсцисс,
Оу – ось ординат,
Оz – ось аппликат.
3.
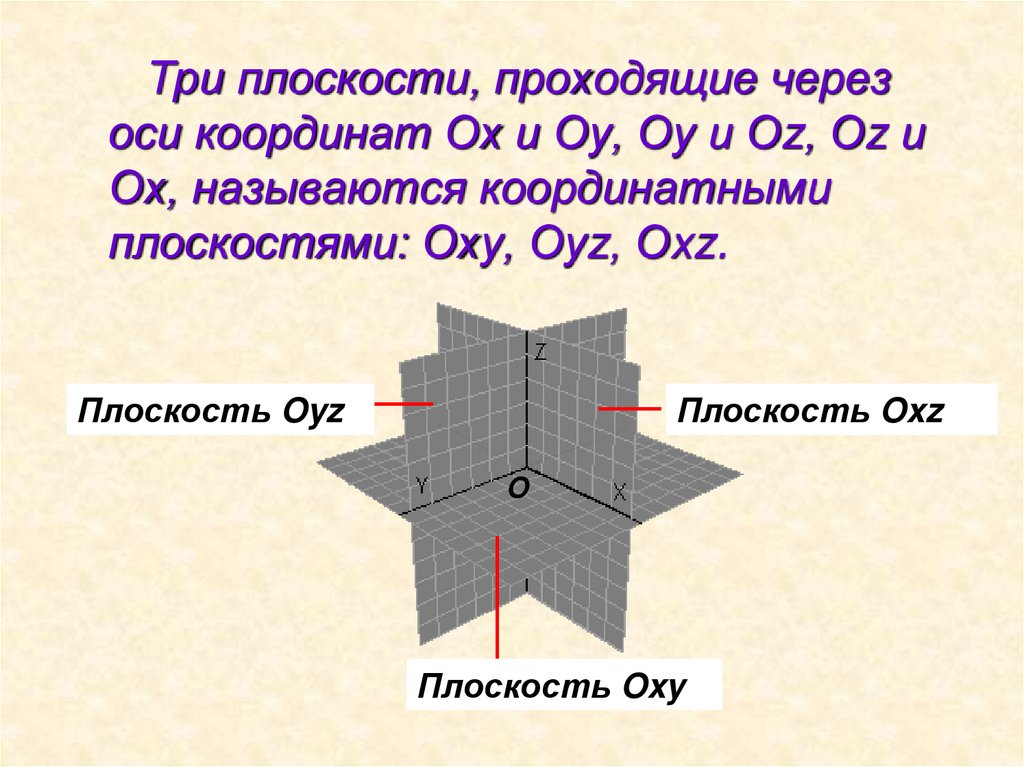
Три плоскости, проходящие черезоси координат Ох и Оу, Оу и Оz, Оz и
Ох, называются координатными
плоскостями: Оху, Оуz, Оxz.
Плоскость Oyz
Плоскость Oxz
O
Плоскость Oxy
4.
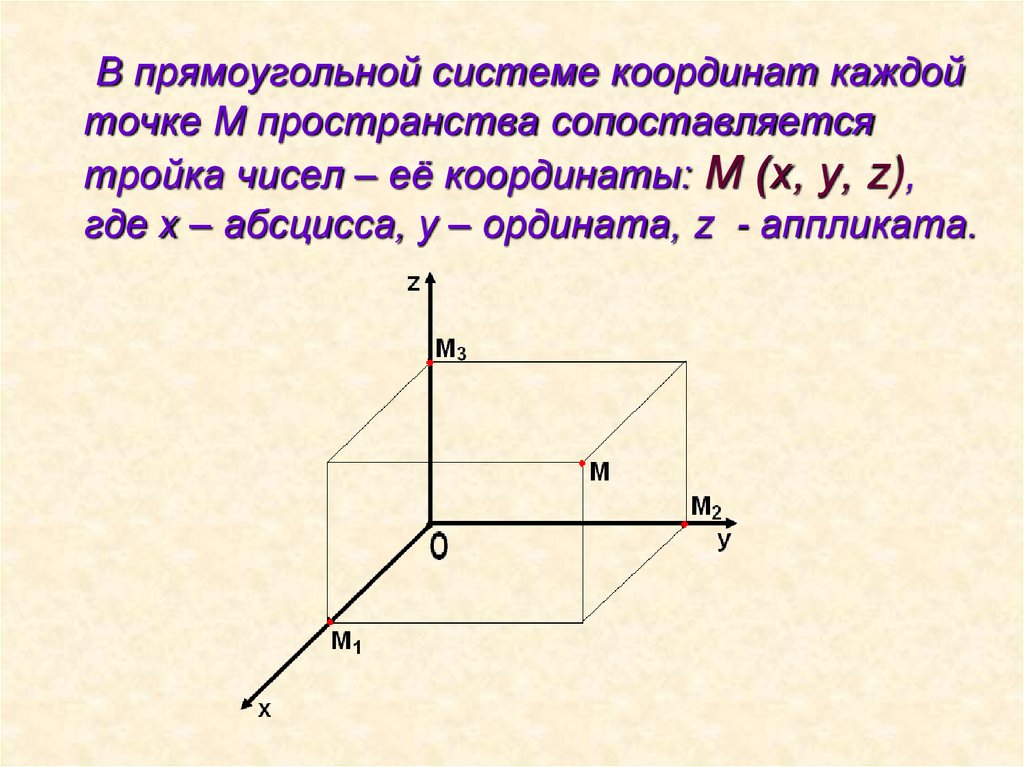
В прямоугольной системе координат каждойточке М пространства сопоставляется
тройка чисел – её координаты: М (х, у, z),
где х – абсцисса, у – ордината, z - аппликата.
5.
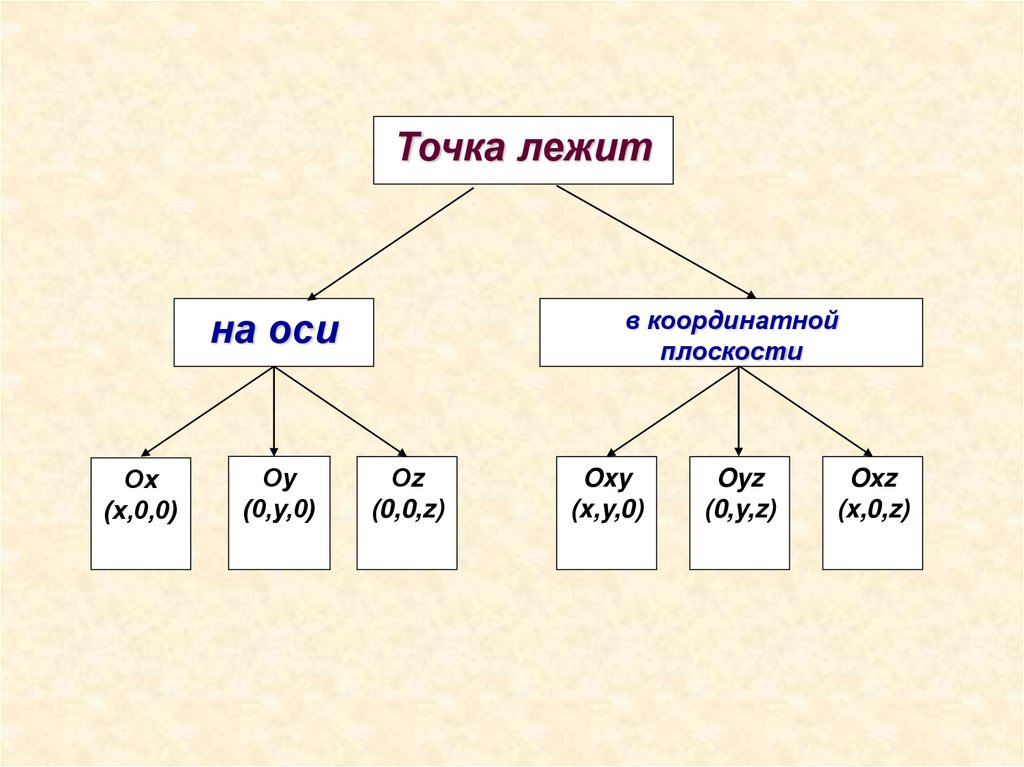
Точка лежитв координатной
плоскости
на оси
Ох
(х,0,0)
Оу
(0,у,0)
Оz
(0,0,z)
Oxy
(x,y,0)
Oyz
(0,y,z)
Oхz
(x,0,z)
6.
Координаты вектора впространстве
7.
Единичный вектор – вектор, длина которого равна 1.i – единичный вектор оси абсцисс, j – единичный вектор
оси ординат, k – единичный вектор оси аппликат.
z
k
j
O
i
x
y
8.
Любой вектор ā можно разложить покоординатным векторам, т.е. представить в
виде:
а хi y j z k
Нулевой вектор можно представить в виде:
0 0i 0 j 0k
Координаты равных векторов соответственно
равны, т.е., если
ā { x1; y1; z1 } = b { x2; y2; z2 }, то
x1 = x2, y1 = y2, z1 = z2.
9.
1. Сумма векторов:a + b = { x1+ x2; y1+ y2; z1+ z2 }.
2. Разность векторов:
a – b = { x1 – x2; y1 – y2; z1 – z2 }.
3. Произведение вектора на
число:
αā = { αx; αy; αz }.
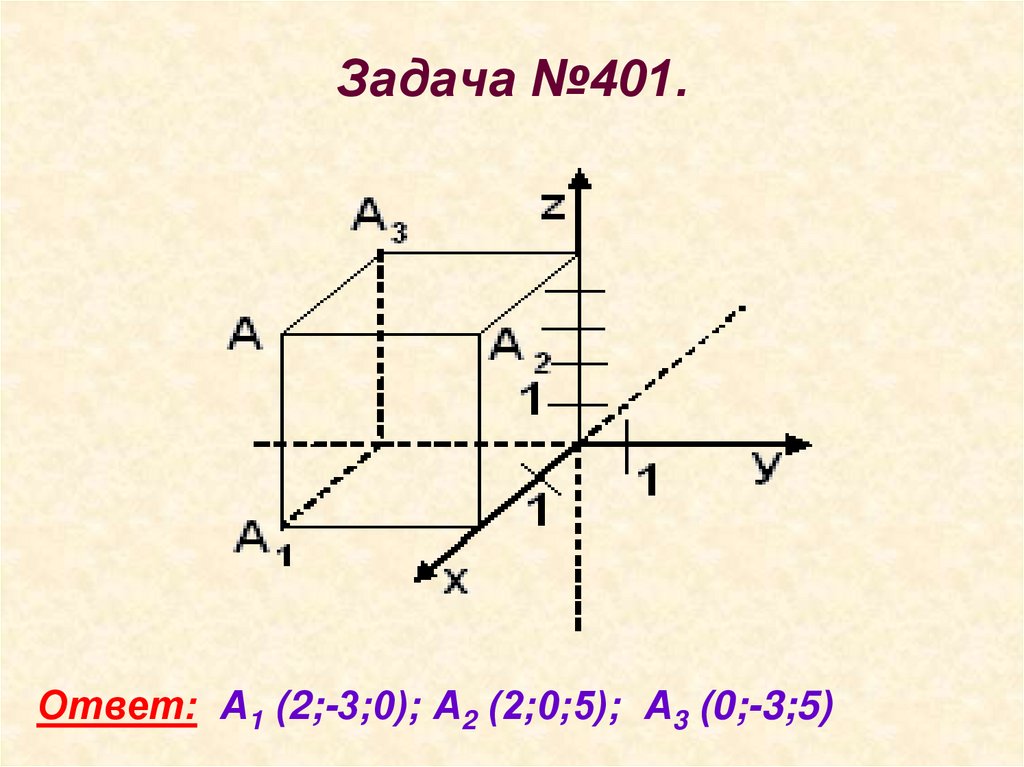
10. Задача №401.
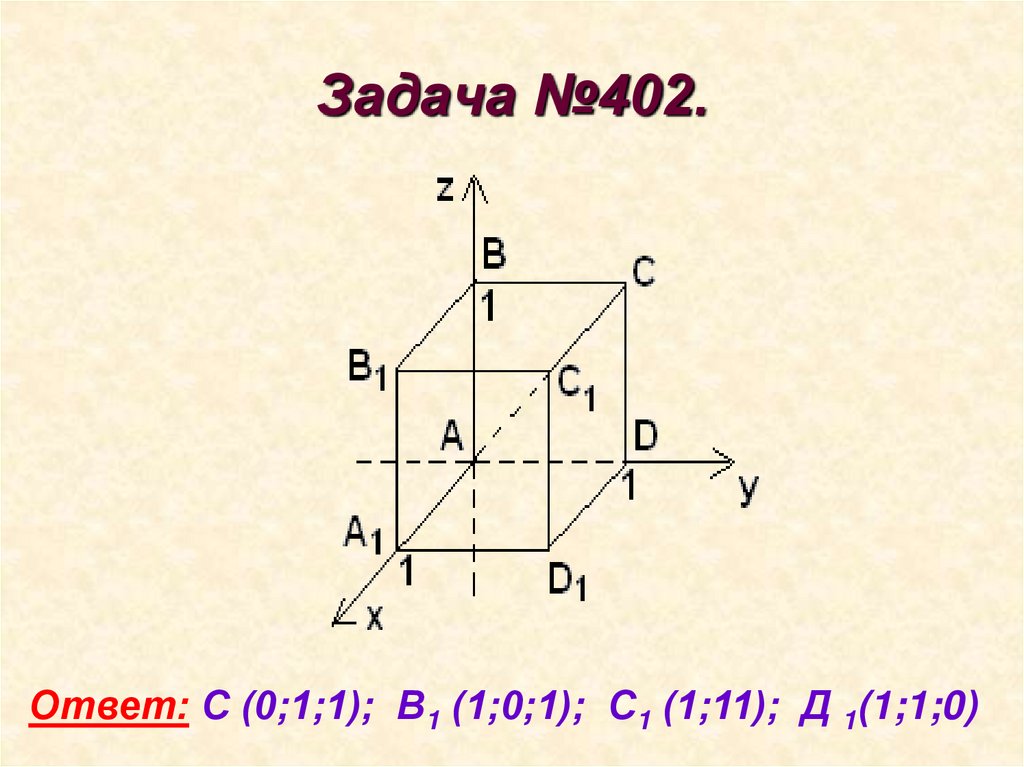
Ответ: А1 (2;-3;0); А2 (2;0;5); А3 (0;-3;5)11. Задача №402.
Ответ: С (0;1;1); В1 (1;0;1); С1 (1;11); Д 1(1;1;0)12.
На уроке познакомились с прямоугольнойсистемой координат, научились строить
точку по заданным ее координатам и
находить координаты точки, изображенной
в заданной системе координат. Декартова
система координат не единственная. К
следующему уроку найти в Интернете
другие системы координат.
13. Разложение вектора по координатным векторам
14.
Векторы называются коллинеарными,если они параллельны.
а
b
с
Если векторы а { x1; y1; z1 } и b { x2; y2; z2 },
то:
х1 у1 z1
k
х2 у 2 z 2
15. Самостоятельная работа
1 вариант2 вариант
№1. Даны векторы
а {2; -4; 3} и b {-3; 1/2; 1}.
Найдите координаты
вектора с = a + b.
№1. Даны векторы
а {1; -3; -1} и b {-1; 2; 0}.
Найдите координаты
вектора с = a – b.
№2. Даны векторы
а {1; -2; 0}, b {3; -6; 0},
c {0; -3; 4}. Найдите
координаты вектора
p = 2a – 1/3b – c.
№2. Даны векторы
а {2; 4; -6}, b {-3; 1; 0},
c {3; 0; -1}. Найдите
координаты вектора
p = -1/2a + 2b – c.
№3. Найдите значения m
и n, при которых
векторы а {6; n; 1} и
b
{m; 16; 2} коллинеарны.
№3. Найдите значения m
и n, при которых
векторы а {-4; m; 2} и
b {2; -6; n} коллинеарны.
16. Связь между координатами векторов и координатами точек
17.
Вектор, конец которого совпадает с данной точкой,а начало – с началом координат, называется радиусвектором данной точки.
Координаты любой точки равны соответствующим
координатам её радус-вектора.
М (x; y; z)
OM (x; y; z)
A (x1; y1; z1), B (x2; y2; z2)
AB (x2 – x1; y2 – y1; z2 – z1)
18. Простейшие задачи в координатах
19.
1. Координаты середины отрезка.z
A (x1; y1; z1), B (x2; y2; z2),
C (x; y; z) – середина АВ.
D
А
С
ОС = ½ (ОА + ОВ), тогда
В
О
х
у
1
1
1
x ( x1 x2 ), y ( y1 y2 ), z ( z1 z2 )
2
2
2
2. Вычисление длины вектора по его
координатам:
если а { x; y; z }, то | a |
x2 y2 z 2
3. Расстояние между двумя точками:
| AB | d ( x2 x1 ) ( y2 y1 ) ( z 2 z1 )
2
2
2
20. Угол между векторами
21.
А^
а
О
а b
α
b
В
• Если а || b и а и b сонаправлены, то α = 0°.
• Если a || b и a и b противоположно
направлены, то α = 180°.
• Если а b, то α = 90°.
22. Скалярное произведение векторов
23.
1) a · b = | a | · | b | · cos(a ^ b)2) a { x1; y1; z1 } и b { x2; y2; z2 }
a · b = x1x2 + y1y2 + z1z2
3) a 2 = | a |2
cos
cos
x1 x2 y1 y2 z1 z 2
x y z x y z
2
1
2
1
a b
| a | | b |
2
1
2
2
2
2
2
2
24.
Решение:№ 467
Введём систему
координат: В(0; 0; 0),
С(1; 0; 0), А(0; 1; 0),
D(1; 1;0), B1(0; 0; 2),
C1(1; 0; 2), D1(1; 1; 2),
A1(0; 1; 2). Тогда,
z
B1
A1
C1
D1
BD{1; 1; 0},
у
B
A
C
х
D
cos
CD1 = BA1{0; 1; 2}.
| 1 0 1 1 0 2 |
12 12 0 2 0 2 12 2 2
1
10
25.
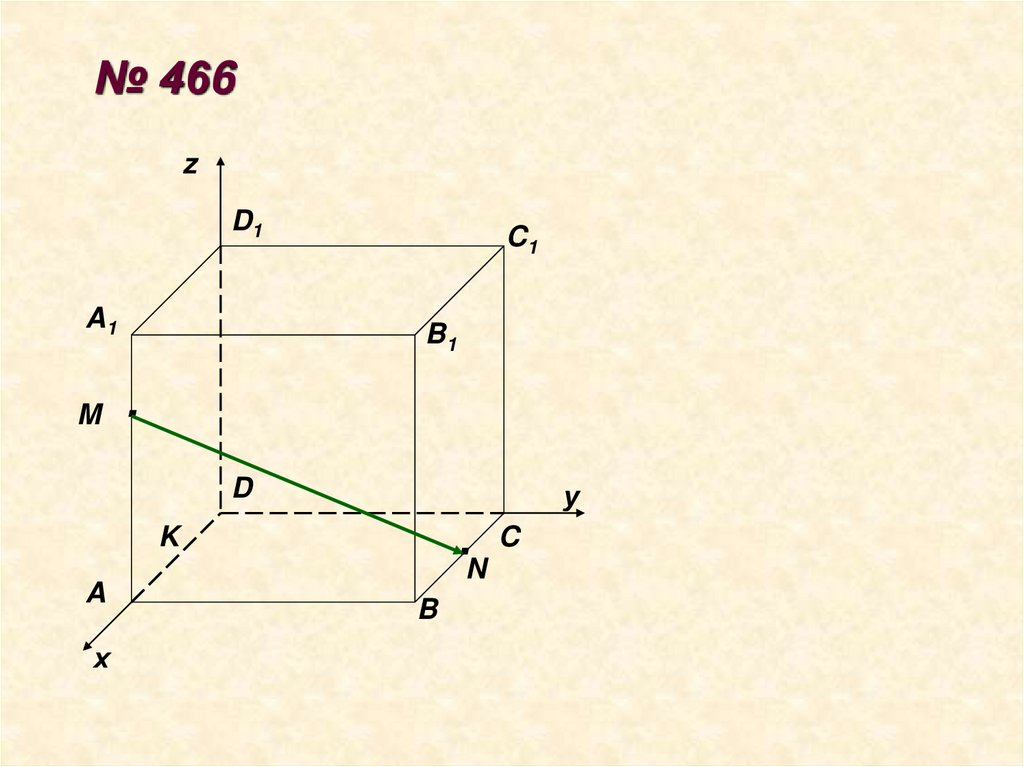
№ 466z
D1
A1
M
C1
B1
.
D
у
. C
K
A
х
N
B
26.
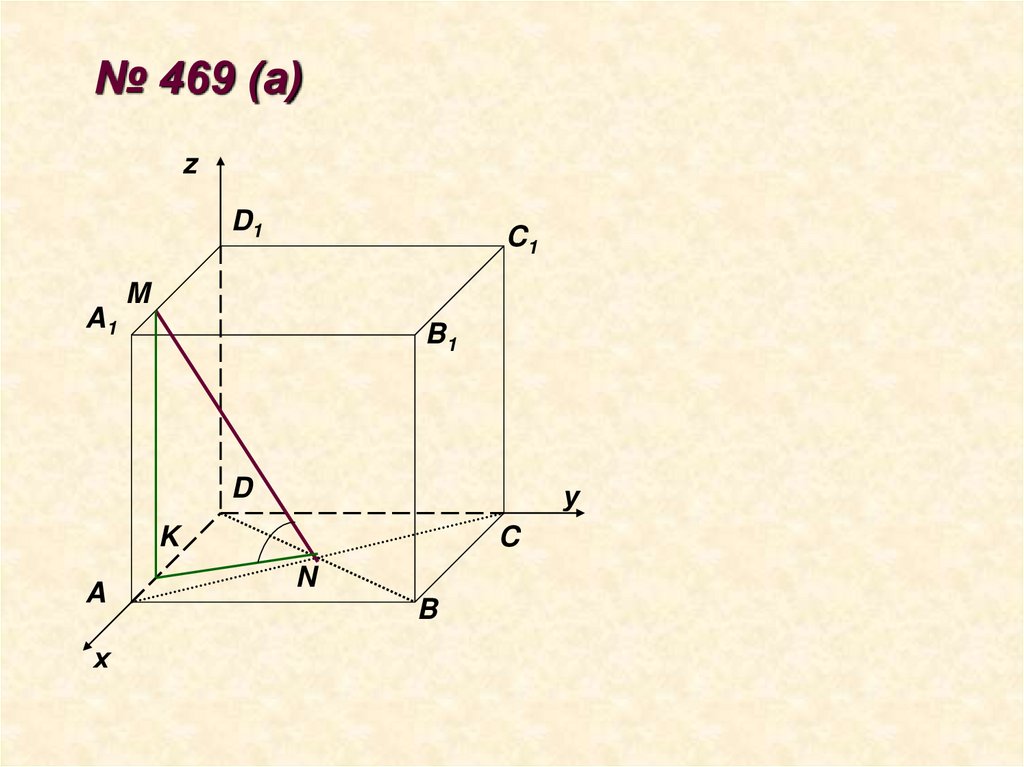
№ 469 (а)z
D1
A1
C1
M
B1
D
у
K
A
х
C
N
B













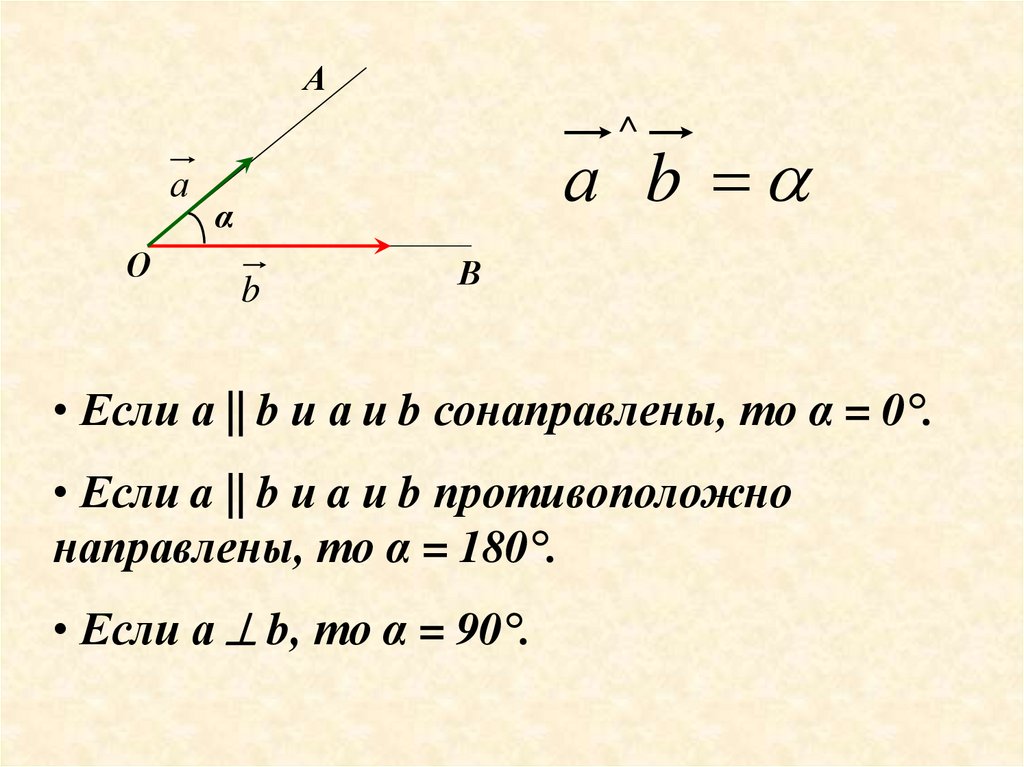

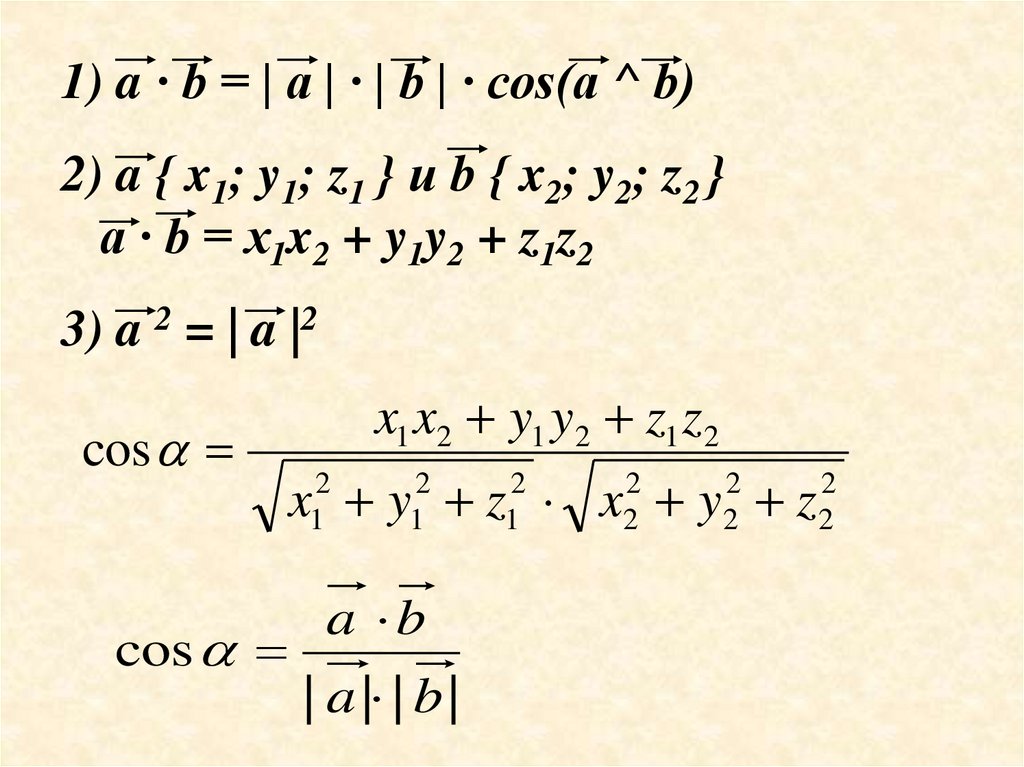

 Математика
Математика








