Моделирование на графах

1. Моделирование ГБОУ школа № 467 Санкт-Петербург 2017 г.

2. Классификации моделей с учётом фактора времени

Модели
Статические
Определение
Пример
Одномоментный
(на
Обследование
учащихся
в
данный
момент поликлинике даёт картину физического
времени)
срез состояния детей на данный момент
информации
по времени.
объекту
Расчёт прочности и устойчивости к
постоянной нагрузке на фундамент, на
стены, на балки при строительстве
здания.
Динамические Позволяют
увидеть
Карточка школьника, отражающая
изменения
состояния состояние здоровья ребенка в течение
объекта во времени
многих
лет
при
воздействии
экологических,
экономических
и
социальных факторов.
Учёт
противодействия
ветрам,
движению грунтовых вод, сейсмическим
колебаниям при строительстве здания

3. Классификация моделей по способу представления

Модели
Определение
Примеры
Материальные
Воспроизводят
геометрические и
физические свойства
объекта и всегда
имеют реальное
воплощение
Детские игрушки, чучела птиц,
карты, схемы, макеты, опыты
и.т.д.
Информацион
ные
Нельзя потрогать или
увидеть воочию так
как они не имеют
материальной
основы, а строятся
только на информации.
Любое описание объекта на одном
из разговорных или формальных
языков

4.

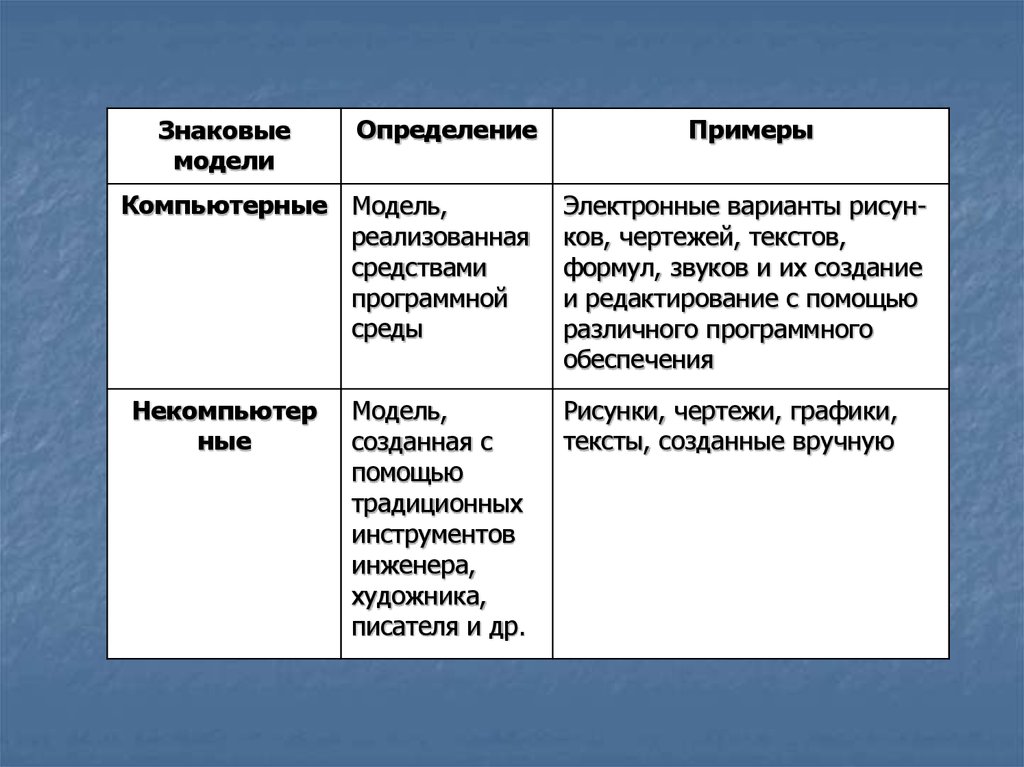
Знаковые
модели
Определение
Компьютерные Модель,
реализованная
средствами
программной
среды
Некомпьютер
ные
Модель,
созданная с
помощью
традиционных
инструментов
инженера,
художника,
писателя и др.
Примеры
Электронные варианты рисунков, чертежей, текстов,
формул, звуков и их создание
и редактирование с помощью
различного программного
обеспечения
Рисунки, чертежи, графики,
тексты, созданные вручную

5. Понятие «Система»

Система - это целое, состоящее из объектов,
взаимосвязанных между собой.
Примеры систем: человек, компьютер, дом, дерево,
книга, стол, науки, обучение в школе и т.д.
Системы бывают:
Материальные (человек, компьютер, дерево, дом).
Нематериальные (человеческий язык, математика)
Смешанные (школьная система, так как включает в
себя как материальные элементы (здание,
оборудование, школьников, учебники), так и
нематериальные (расписание занятий, темы уроков,
устав школы).

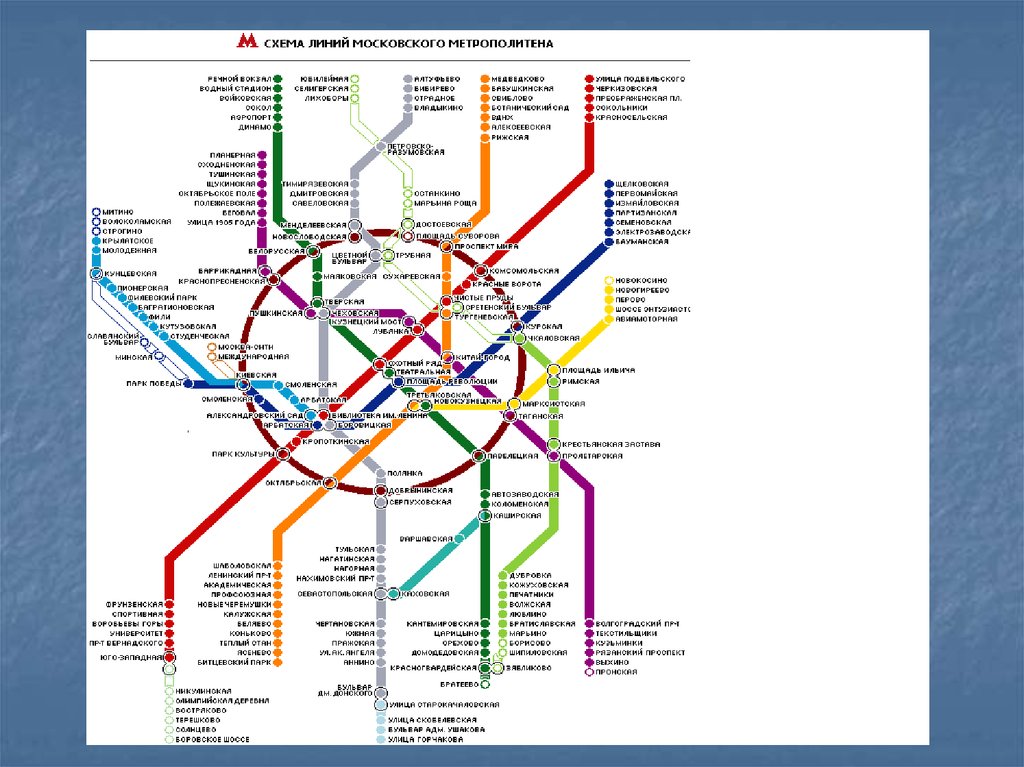
6.

Граф – это средство для наглядного
представления состава и структуры
системы
Граф состоит из вершин,
связанных дугами или рёбрами.

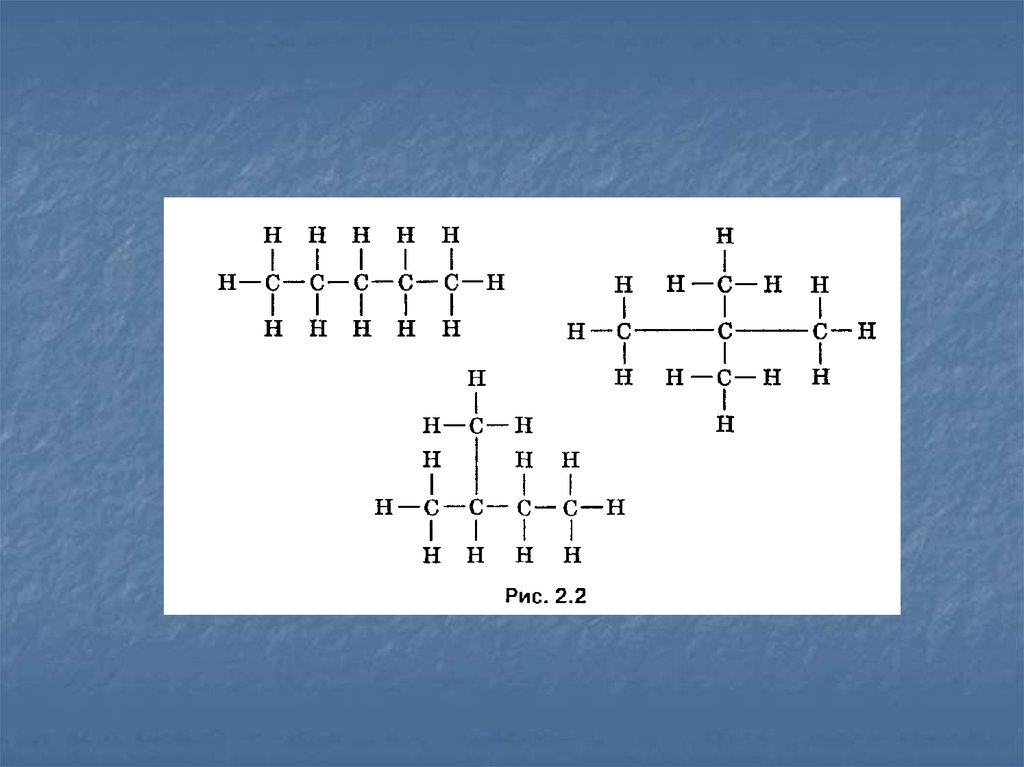
7. Информационные модели в графах

Вершины могут быть изображены кругами, овалами,
точками, прямоугольниками и пр. Связи между
вершинами изображаются линиями. Если линия
направленная (т.е. со стрелкой), то она называется
дугой, если не направленная (без стрелки), то
ребром. Принято считать, что одно ребро заменяет
две дуги, направленные в противоположные
стороны. Граф, в котором все линии направленные,
называется ориентированным графом. Две вершины,
соединенные дугой или ребром, называются
смежными.

8.

9.

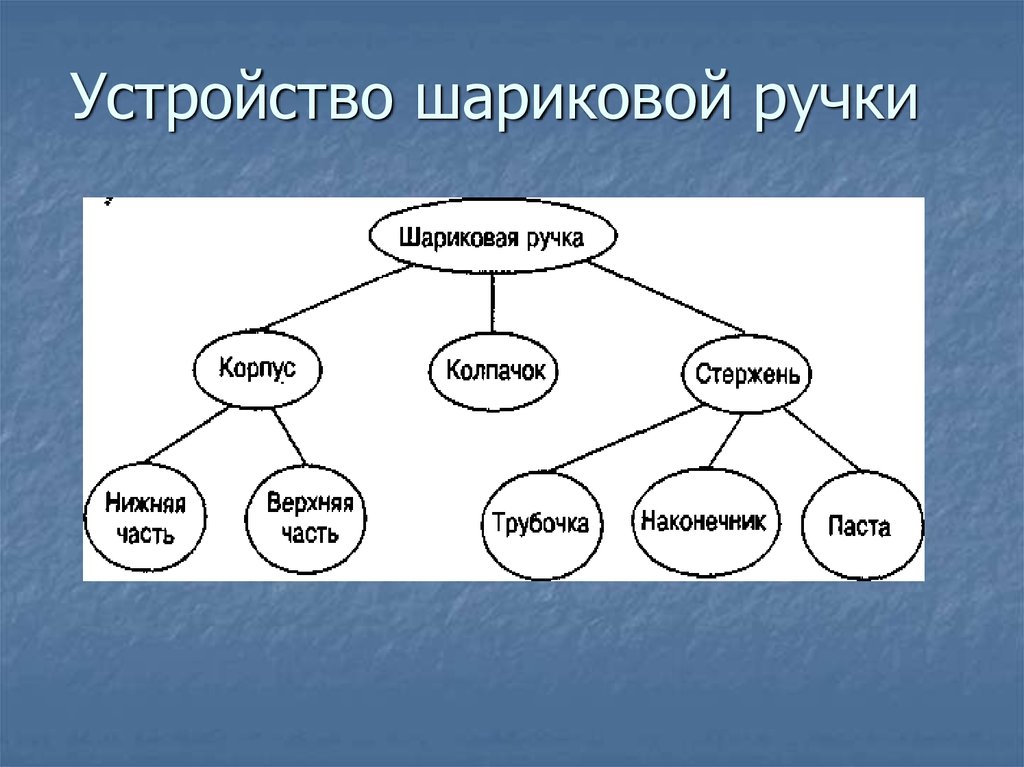
10. Устройство шариковой ручки

11.

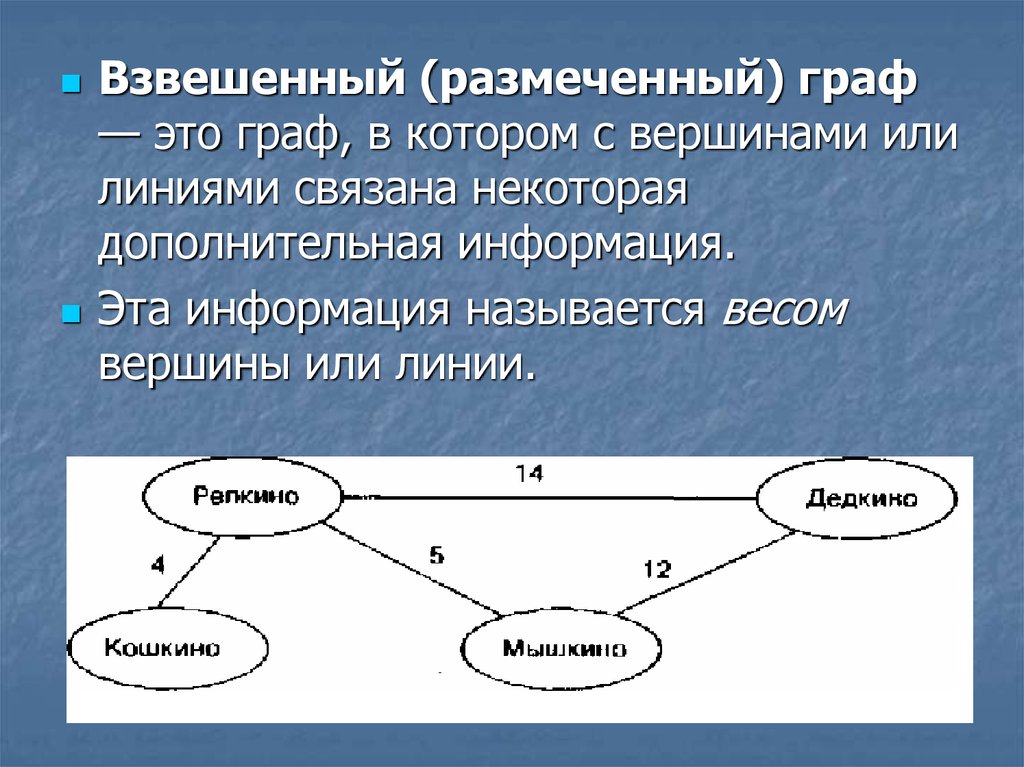
Взвешенный (размеченный) граф
— это граф, в котором с вершинами или
линиями связана некоторая
дополнительная информация.
Эта информация называется весом
вершины или линии.

12.

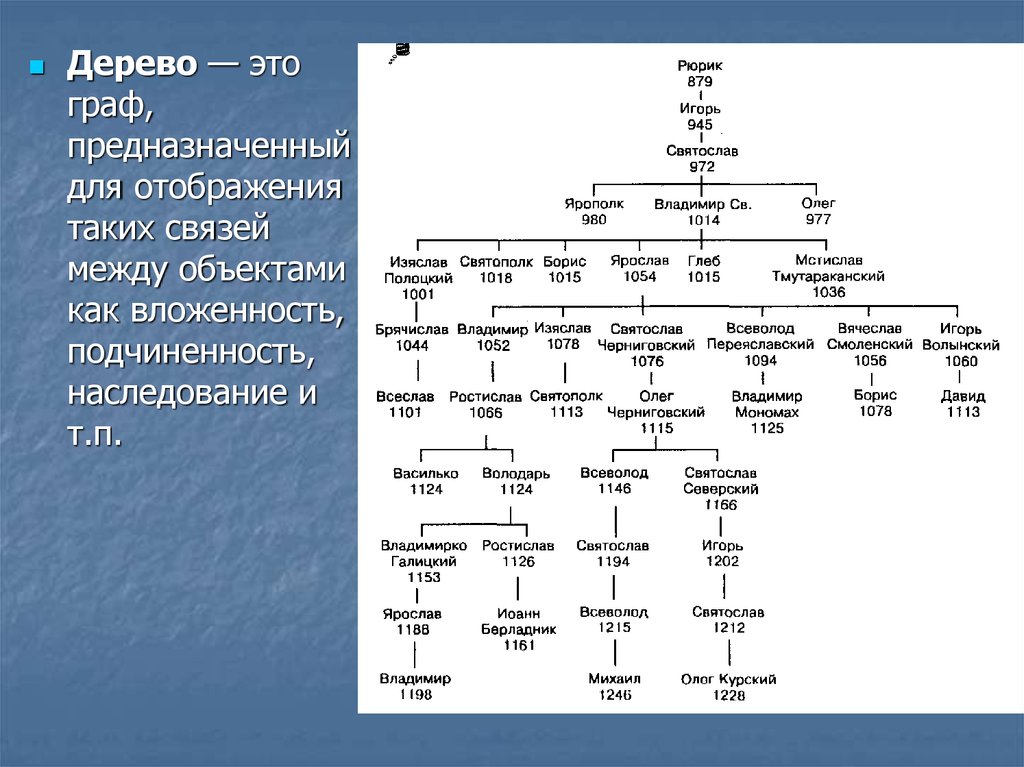
Дерево — это
граф,
предназначенный
для отображения
таких связей
между объектами
как вложенность,
подчиненность,
наследование и
т.п.

13.

14.

Решим частную задачу: разделим произвольный
отрезок на три равных части. Реализуем решение
данной задачи с помощью графического редактора
Paint.
1 шаг
С помощью инструмента ЛИНИЯ чертим отрезок длиной
а
а

15.

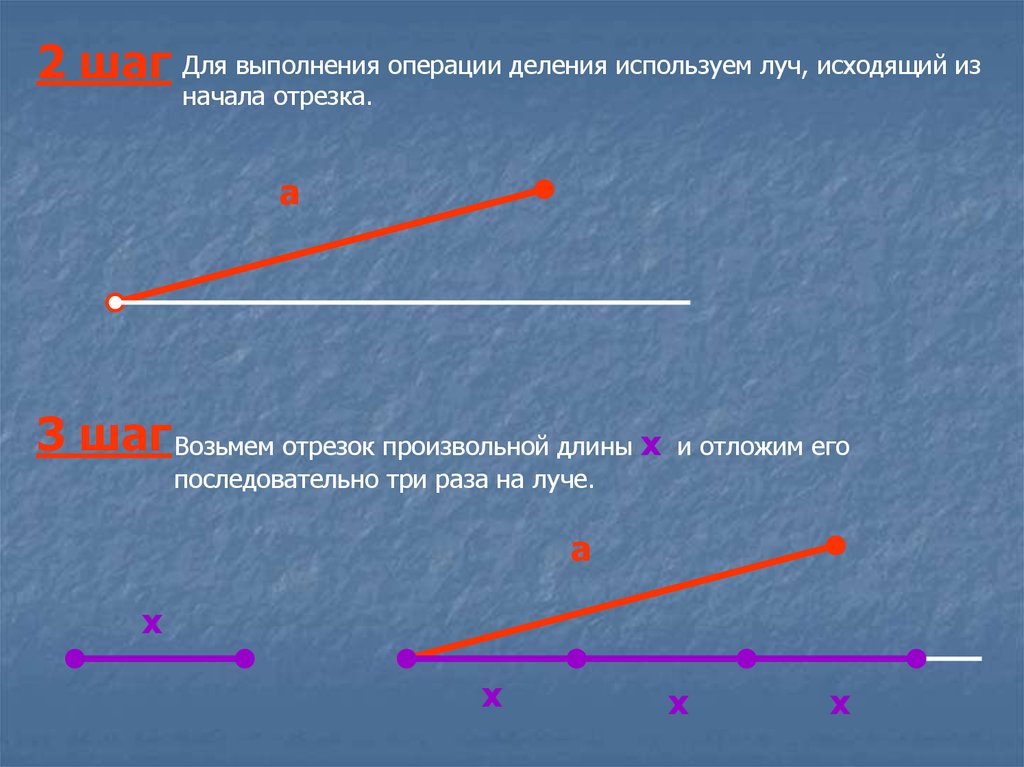
2 шаг Для выполнения операции деления используем луч, исходящий из
начала отрезка.
а
3 шаг Возьмем отрезок произвольной длины х
и отложим его
последовательно три раза на луче.
а
х
х
х
х

16.

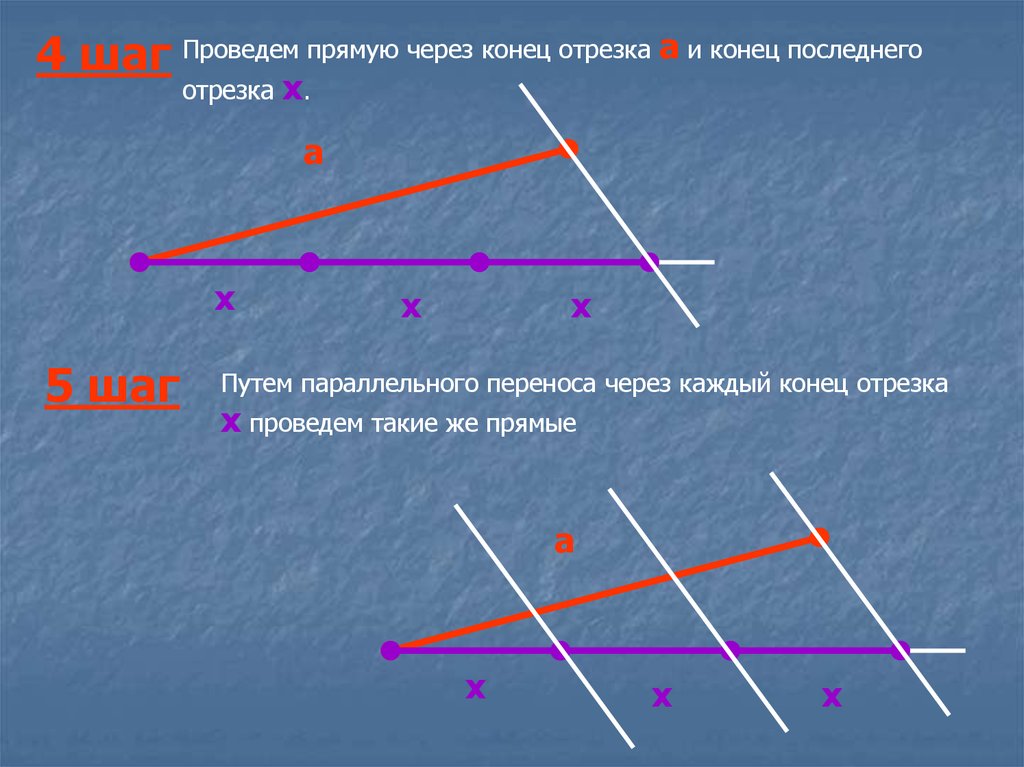
4 шаг Проведем прямую через конец отрезка а и конец последнего
отрезка
х.
а
х
5 шаг
х
х
Путем параллельного переноса через каждый конец отрезка
х проведем такие же прямые
а
х
х
х

17.

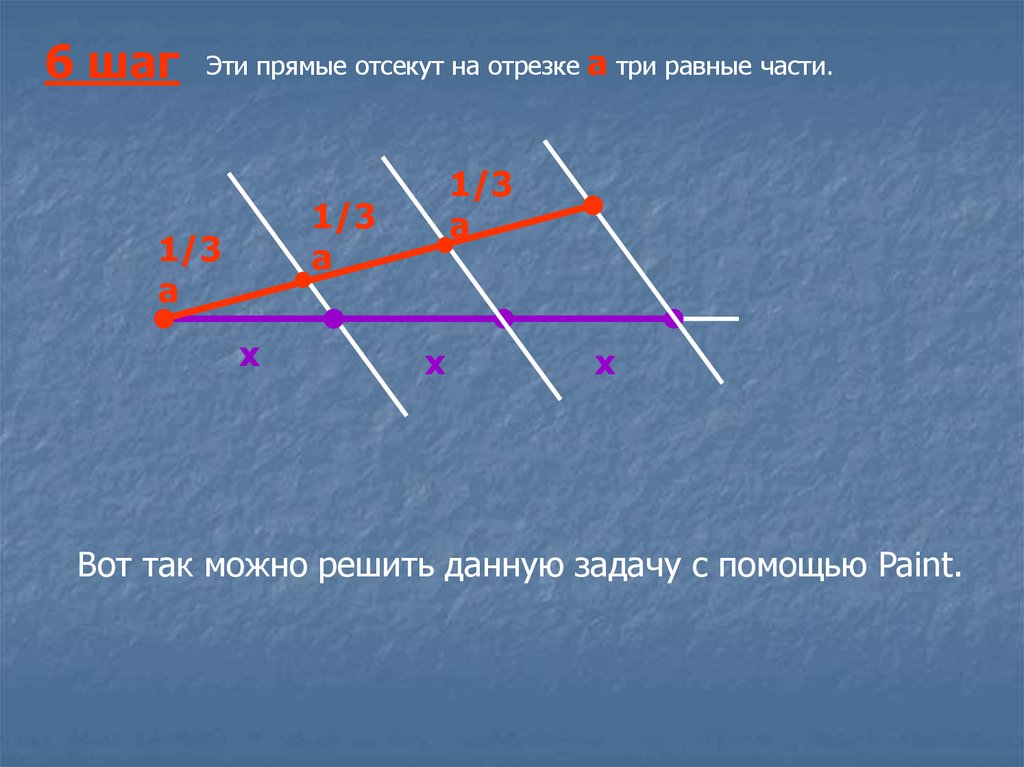
6 шаг
Эти прямые отсекут на отрезке
1/3
а
1/3
а
1/3
а
х
а три равные части.
х
х
Вот так можно решить данную задачу с помощью Paint.

18.

Построение
равнобедренного
треугольника по заданному
h
основанию и высоте
a

19.

Описание задачи:
Вся история геометрии связана с практикой построений при
помощи подручных средств для измерения недоступного.
Задача построения равнобедренного треугольника по основанию
и высоте опирается на знания, полученные ещё в древности.
Основная часть построения заключается в делении отрезка,
задающего основание, на две равные части.
Выполнение этой операции не составит труда при помощи
циркуля и линейки, но всё усложняется в графическом
редакторе, т. к. возможности его ограничены.
Наша задача – показать на данном примере, как геометрические
построения, возможные на бумаге с использованием различных
инструментов, можно реализовать в редакторе Paint.

20.

Цель моделирования:
•При отсутствии циркуля и линейки смоделировать операции
деления отрезка на две равные части и построения
равнобедренного треугольника.
•Научиться эффективно использовать инструменты графического
редактора.

21.

Высота в равнобедренном треугольнике одновременно является
и медианой.
Алгоритм построения сводится к повороту отрезка, задающего
высоту, на 900 и к делению отрезка, задающего основание,
пополам.
• С помощью инструмента «линия»
построим два произвольных
горизонтальных отрезка. Это будут
высота (h) и основание (a) нашего
будущего равнобедренного
треугольника.
• Чтобы линии были ровными и
строго горизонтальными используйте
нажатой кнопку «шифт» во время
рисования.
• С помощью инструмента
«выделение» выделим отрезок (h)
и повернём его на 900 (Рисунок Отразить/Повернуть - Повернуть на
угол 90).
Это будет высотой треугольника.
a
h

22.

Теперь нужно разделить отрезок, задающий основание на
пополам.
Для этого:
• Выделим нужный отрезок и
переместим его на свободное
место.
• С помощью инструмента
«линия» в сочетании с нажатой
клавишей «шифт» из начала
отрезка вниз слева - напрово под
углом 450 построим прямую
некоторой длины.
•Аналогично из конца отрезка
вниз справа – налево
построим ещё одну прямую
под углом 450, пересекающую
предыдущую.
С помощью этих дополнительных
построений мы получили
равнобедренный треугольник. Теперь из
вершины (точки пересечения
дополнительных прямых) построим
высоту данного треугольника, которая
как мы знаем, является так же и
медианой.

23.

Мы нашли середину основания треугольника и теперь из этой
точки можно построить его медиану, которая является и высотой.
Для этого:
• Выделим отрезок и переместим
его к середине основания.
• Теперь осталось лишь выбрать
инструмент «линия» и провести
две линии, соединяющие высоту
треугольника с его основанием.
•Наш треугольник практически
готов, осталось теперь
воспользоваться инструментом
«Ластик/Цветной ластик» и
убрать ненужные
дополнительные построения.
Треугольник, построенный
по основанию и высоте
готов!
h
a