Похожие презентации:
Vectors. Lecture 9
1.
VectorsKARASHBAYEVA ZH.O., SENIOR-LECTURER
2.
Contents:Scalar product of vectors and its properties
Vector product of vectors and its properties
Mixed product of vectors and its properties
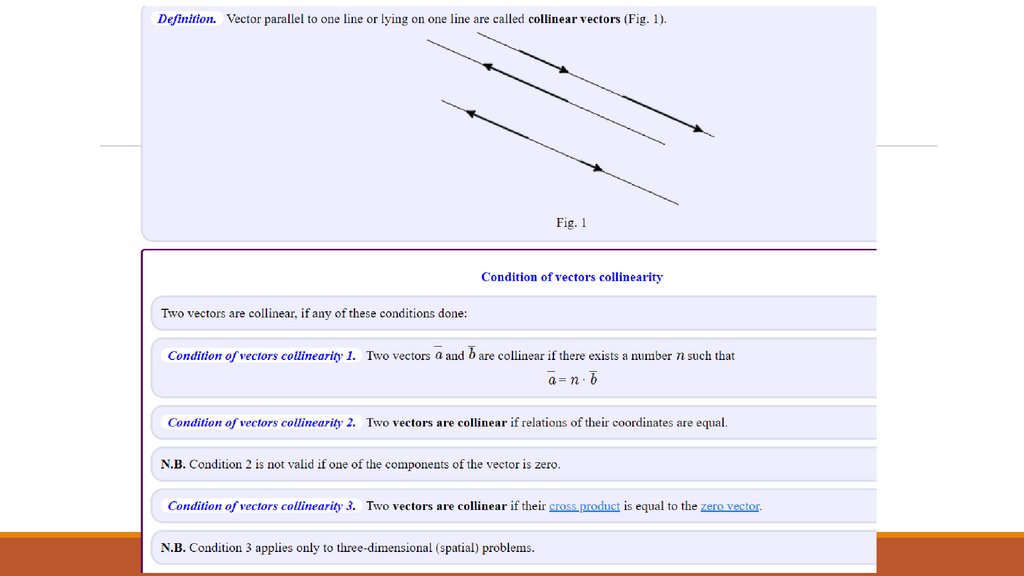
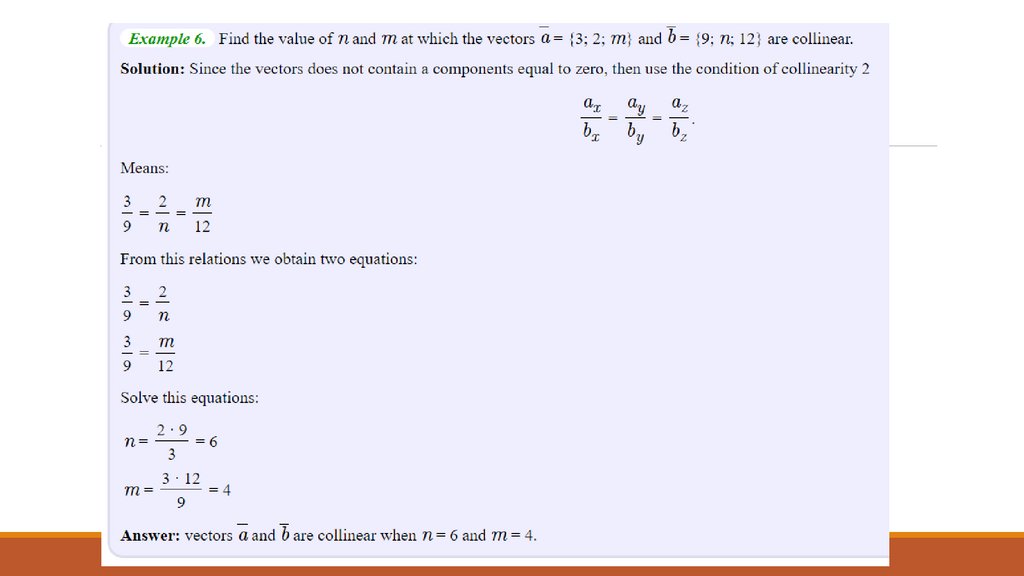
Collinear and coplanar vectors
3.
THE DOT PRODUCTDefinition 1
• If a = ‹a1, a2, a3› and b = ‹b1, b2, b3›, then
the dot product of a and b is the number a • b given by:
a • b = a1b1 + a2b2 + a3b3
4.
SCALAR PRODUCTThe result is not a vector.
It is a real number, that is, a scalar.
◦ For this reason, the dot product is sometimes
called the scalar product (or inner product).
5.
DOT PRODUCTThough Definition 1 is given for three-dimensional (3-D) vectors, the dot product
of two-dimensional vectors is defined in
a similar fashion:
‹a1, a2› ∙ ‹b1, b2› = a1b1 + a2b2
6.
PROPERTIES OF DOT PRODUCTIf a, b, and c are vectors in V3 and c is a scalar, then
1. a a=|a|
2. a b = b a
3. a (b + c) = a b + a c
4. (ca) b = c(a b) = a (cb)
5. 0 a = 0
2
7.
DOT PRODUCT PROPERTY 1a∙a
2
2
2
= a1 + a2 + a3
2
= |a|
Proof
8.
DOT PRODUCT PROPERTY 3a • (b + c)
= ‹a1, a2, a3› ∙ ‹b1 + c1, b2 + c2, b3 + c3›
= a1(b1 + c1) + a2(b2 + c2) + a3(b3 + c3)
= a1b1 + a1c1 + a2b2 + a2c2 + a3b3 + a3c3
= (a1b1 + a2b2 + a3b3) + (a1c1 + a2c2 + a3c3)
=a∙b+a∙c
Proof
9.
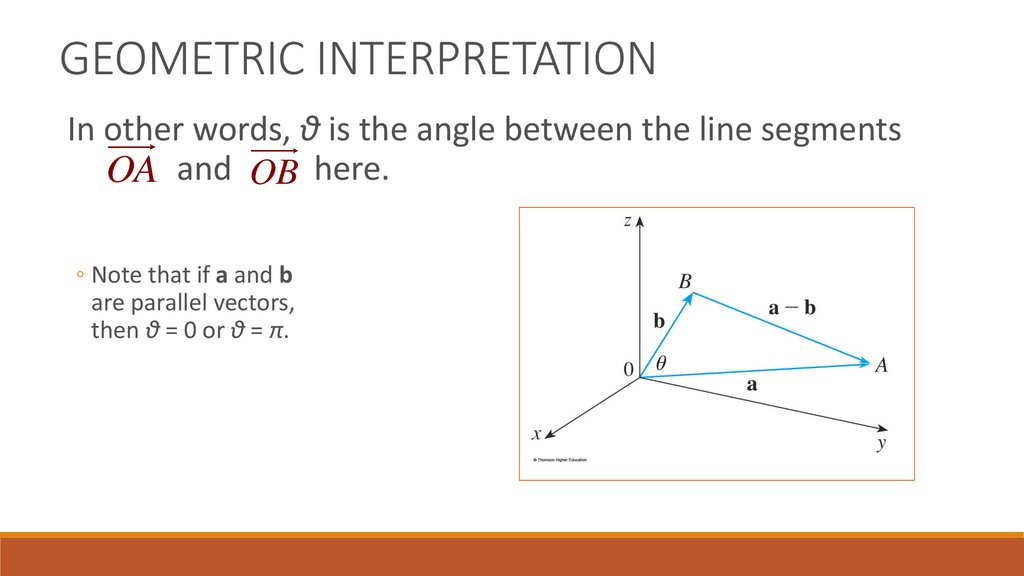
GEOMETRIC INTERPRETATIONThe dot product a • b can be given a geometric interpretation in terms of the angle θ
between a and b.
◦ This is defined to be the angle between the representations of a and b that start
at the origin, where 0 ≤ θ ≤ π.
10.
GEOMETRIC INTERPRETATIONIn other words, θ is the angle between the line segments
OA and OB here.
◦ Note that if a and b
are parallel vectors,
then θ = 0 or θ = π.
11.
DOT PRODUCT—DEFINITIONIf θ is the angle between the vectors
a and b, then
a ∙ b = |a||b| cos θ
Theorem
12.
DOT PRODUCT—DEFINITIONIf we apply the Law of Cosines to triangle OAB here, we get:
|AB|2 = |OA|2 + |OB|2 – 2|OA||OB| cos θ
◦ Observe that
the Law of Cosines
still applies in
the limiting cases
when θ = 0 or π, or
a = 0 or b = 0
Proof—Equation 1
13.
DOT PRODUCT—DEFINITIONSo, Equation 1 becomes:
|a – b|2 = |a|2 + |b|2 – 2|a||b| cos θ
Proof—Equation 2
14.
DOT PRODUCT—DEFINITIONProof
Using Properties 1, 2, and 3 of the dot product, we can rewrite the left side of
the equation as follows:
|a – b|2 = (a – b) ∙ (a – b)
=a∙a–a∙b–b∙a+b∙b
= |a|2 – 2a ∙ b + |b|2
15.
DOT PRODUCT—DEFINITIONTherefore, Equation 2 gives:
|a|2 – 2a ∙ b + |b|2 = |a|2 + |b|2 – 2|a||b| cos θ
◦ Thus,
or
–2a ∙ b = –2|a||b| cos θ
a ∙ b = |a||b| cos θ
Proof
16.
THE CROSS PRODUCTThe cross product a x b of two vectors a and b, unlike the
dot product, is a vector.
◦ For this reason, it is also called the vector product.
◦ Note that a x b is defined only when a and b are three-dimensional (3-D)
vectors.
17.
THE CROSS PRODUCTIf a = ‹a1, a2, a3› and b = ‹b1, b2, b3›, then
the cross product of a and b is the vector
a x b = ‹a2b3 - a3b2, a3b1 - a1b3, a1b2 - a2b1›
Definition 2
18.
CROSS PRODUCTEquation 3
We see that the cross product of the vectors
a = a1i +a2j + a3k and b = b1i + b2j + b3k
is:
a2
a b =
b2
a3
a1 a3
a1 a2
i−
j+
k
b3
b1 b3
b1 b2
i
j
a b = a1 a2
b1 b2
k
a3
b3
19.
CROSS PRODUCTExample 1
If a = <1, 3, 4> and b = <2, 7, –5>, then
i j k
a b = 1 3 4
2 7 −5
3 4
1 4
1 3
=
i−
j+
k
7 −5
2 −5
2 7
= (−15 − 28)i − (−5 − 8) j + (7 − 6)k
= −43i + 13 j + k
20.
CROSS PRODUCTExample 2
Show that a x a = 0 for any vector a in V3.
◦ If a = <a1, a2, a3>,
then
i
a a = a1
a1
j
a2
a2
k
a3
a3
= (a2 a3 − a3 a2 ) i − (a1a3 − a3a1 ) j
+ (a1a2 − a2 a1 ) k
= 0i − 0 j+ 0k = 0
21.
CROSS PRODUCTTheorem
The vector a x b is orthogonal to both a and b.
22.
CROSS PRODUCTProof
In order to show that a x b is orthogonal to
a, we compute their dot product as follows
(a b) a
a2
=
b2
a3
a1
a1 −
b3
b1
a3
a1
a2 +
b3
b1
a2
a3
b2
= a1 (a2b3 − a3b2 ) − a2 (a1b3 − a3b1 ) + a3 (a1b2 − a2b1 )
= a1a2b3 − a1b2 a3 − a1a2b3 + b1a2 a3 + a1b2 a3 − b1a2 a3
=0
23.
CROSS PRODUCTLet a and b be represented by directed
line segments with the same initial point,
as shown.
Then, the cross product a x b points in a direction
perpendicular to the plane through a and b.
24.
CROSS PRODUCTIt turns out that the direction of a x b is given by the right-hand rule, as follows.
If the fingers of your right hand curl in the direction of a rotation (through an angle
less than 180°) from a to b, then your thumb points in the direction of a x b.
25.
CROSS PRODUCTWe know the direction of the vector a x b.
The remaining thing we need to complete its geometric description is its
length |a x b|.
◦ This is given by the following theorem.
If θ is the angle between a and b (so 0 ≤ θ ≤ π), then
|a x b| = |a||b| sin θ
26.
CROSS PRODUCTProof
From the definitions of the cross product and length of a vector, we have:
|a x b|2 = (a2b3 – a3b2)2 + (a3b1 – a1b3)2 + (a1b2 – a2b1)2
= a22b32 – 2a2a3b2b3 + a32b22 + a32b12 – 2a1a3b1b3 + a12b32 + a12b22 – 2a1a2b1b2 + a22b12
= (a12 + a22 + a32)(b12 + b22 + b32) – (a1b1 + a2b2 + a3b3)2
= |a|2|b|2 – (a . b)2
= |a|2|b|2 – |a|2|b|2 cos2θ
= |a|2|b|2 (1 – cos2θ)
= |a|2|b|2 sin2θ
27.
CROSS PRODUCTTaking square roots and observing that
Proof
sin = sin
2
because sin θ ≥ 0 when
0 ≤ θ ≤ π, we have:
|a x b| = |a||b| sin θ
The length of the cross product a x b is equal to the area of the parallelogram
determined by a and b.
28.
CROSS PRODUCTExample 3
Find a vector perpendicular to the plane that passes through
the points
P(1, 4, 6), Q(-2, 5, -1), R(1, -1, 1)
29.
CROSS PRODUCTExample 3
The vector PQ PR is perpendicular to both PQ and PR .
◦ Therefore, it is perpendicular to the plane through P, Q, and R.
PQ = (−2 − 1) i + (5 − 4) j + (−1 − 6) k
= −3i + j − 7k
PR = (1 − 1) i + (−1 − 4) j + (1 − 6) k
= −5 j − 5k
30.
CROSS PRODUCTExample 3
We compute the cross product of these vectors:
i
j k
PQ PR = −3 1 −7
0 −5 −5
= (−5 − 35) i − (15 − 0) j + (15 − 0) k
= −40i − 15 j + 15k
Therefore, the vector ‹-40, -15, 15› is perpendicular to the given plane.
◦ Any nonzero scalar multiple of this vector,
such as ‹-8, -3, 3›, is also perpendicular
to the plane.
31.
CROSS PRODUCTExample 4
Find the area of the triangle with vertices
P(1, 4, 6), Q(-2, 5, -1), R(1, -1, 1)
32.
CROSS PRODUCTExample 4
In Example 3, we computed that
PQ PR = −40, −15,15
◦ The area of the parallelogram with adjacent sides PQ and
PR is the length of this cross product:
PQ PR = (−40) 2 + (−15) 2 + 152 = 5 82
The area A of the triangle PQR is half the area of this parallelogram, that is: 52
82
33.
CROSS PRODUCT PROPERTIESIf a, b, and c are vectors and c is a scalar, then
1. a x b = –b x a
2. (ca) x b = c(a x b) = a x (cb)
3. a x (b + c) = a x b + a x c
4. (a + b) x c = a x c + b x c
5. a · (b x c) = (a x b) · c
6. a x (b x c) = (a · c)b – (a · b)c
Theorem
34.
CROSS PRODUCT PROPERTY 5Let
a = <a1, a2, a3>,
b = <b1, b2, b3>, c = <c1, c2, c3>
Then,
a · (b x c) = a1(b2c3 – b3c2) + a2(b3c1 – b1c3) + a3(b1c2 – b2c1)
= a1b2c3 – a1b3c2 + a2b3c1 – a2b1c3 + a3b1c2 – a3b2c1
= (a2b3 – a3b2)c1 + (a3b1 – a1b3)c2+ (a1b2 – a2b1)c3
=(a x b) · c
Proof—Equation 4
35.
SCALAR TRIPLE PRODUCTThe product a . (b x c) that occurs
in Property 5 is called the scalar triple product
of the vectors a, b, and c.
a1 a2
a (b c) = b1 b2
c1 c2
a3
b3
c3
36.
SCALAR TRIPLE PRODUCTSThe geometric significance of the scalar triple product can be seen by considering
the parallelepiped determined by the vectors a, b, and c.
37.
SCALAR TRIPLE PRODUCTSThe area of the base parallelogram is:
A = |b x c|
If θ is the angle between a and b x c,
then the height h of the parallelepiped is:
h = |a||cos θ|
We must use |cos θ| instead of cos θ in
case θ > π/2.
38.
SCALAR TRIPLE PRODUCTSHence, the volume of the parallelepiped is:
V = Ah
= |b x c||a||cos θ|
= |a · (b x c)|
◦ Thus, we have proved the following formula.
The volume of the parallelepiped determined by the vectors a, b, and c is the magnitude of
their scalar triple product:
V = |a ·(b x c)|








































 Математика
Математика








