Похожие презентации:
Vectors. Lecture 8
1. Lecture 8. Vectors
Karashbayeva Zh.O.2. Contents
Linear dependence of vectors
Basis on the plane and in space
Decomposition of a vector by basis
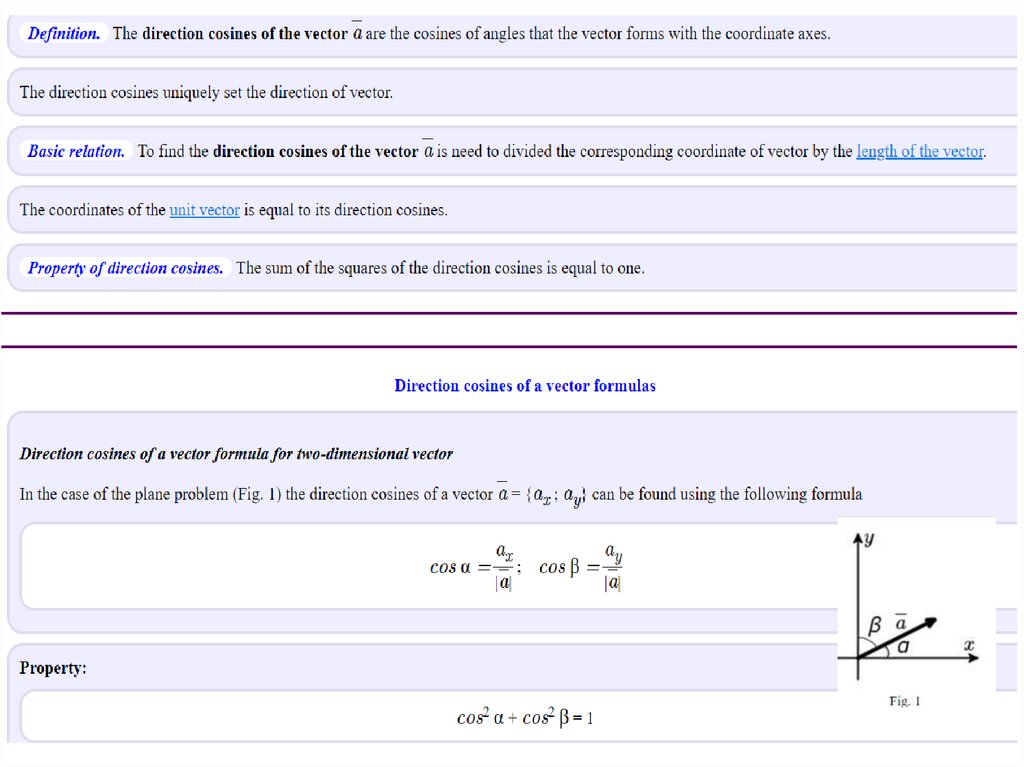
Direction cosines of a vector.
Division of segment.
3. Linear combination
Linear combination :A vector u in a vector space V is called a linear combination of
the vectors v1 , v 2 , , v k in V if u can be written in the form
u c1v1 c2 v 2
where c1 , c2 ,
ck v k ,
, ck are real-number scalars
4.
Ex : Finding a linear combinationv1 (1,2,3) v 2 (0,1,2) v3 ( 1,0,1)
Prove (a) w (1,1,1) is a linear combination of v1 , v 2 , v 3
(b) w (1, 2,2) is not a linear combination of v1 , v 2 , v 3
Sol:
(a) w c1v1 c2 v 2 c3 v3
1,1,1 c1 1,2,3 c2 0,1,2 c3 1,0,1
(c1 c3 , 2c1 c2 , 3c1 2c2 c3 )
c1
c3
2c1 c2
1
1
3c1 2c2 c3
1
5.
1 0 1 1G.-J. E.
2 1 0 1
3 2 1 1
1 0 1 1
0 1 2 1
0 0 0 0
c1 1 t , c2 1 2t , c3 t
(this system has infinitely many solutions)
t 1
w 2 v1 3v 2 v 3
t 2
w 3v1 5v 2 2 v 3
6.
(b)w c1 v1 c2 v 2 c3 v 3
1 0 1 1
2 1 0 2
3 2 1
2
G.-J. E.
1 0 1 1
0 1 2 4
0 0 0
7
This system has no solution since the third row means
0 c1 0 c2 0 c3 7
w can not be expressed as c1v1 c2 v 2 c3 v3
7.
8.
Definitionsof Linear Independence (L.I.) and Linear Dependence
(L.D.) :
S v1 , v2 ,
For c1v1 c2 v 2
, vk : a set of vectors in a vector space V
ck v k 0
(1) If the equation has only the trivial solution (c1 c2
then S (or v1 , v 2 ,
ck 0)
, v k ) is called linearly independent
(2) If the equation has a nontrivial solution (i.e., not all zeros),
then S (or v1 , v 2 ,
, v k ) is called linearly dependent (The name of
linear dependence is from the fact that in this case, there exist a v i
which can be represented by the linear combination of {v1 , v 2 ,
v i 1 ,
v k } in which the coefficients are not all zero.
, v i 1 ,
9.
Ex : Testing for linear independenceDetermine whether the following set of vectors in R3 is L.I. or L.D.
S v1 , v 2 , v 3 1, 2, 3 , 0, 1, 2 , 2, 0, 1
Sol:
c1
c1v1 c2 v 2 c3 v 3 0
2c3 0
2c1 c2
0
3c1 2c2 c3 0
1 0 2 0
1 0 0 0
G.-J. E.
2 1 0 0
0 1 0 0
3 2 1 0
0 0 1 0
c1 c2 c3 0 only the trivial solution
(or det(A) 1 0, so there is only the trivial solution)
S is (or v1, v 2 , v3 are) linearly independent
10.
• EX: Testing for linear independenceDetermine whether the following set of vectors in P2 is L.I. or L.D.
S v1 , v 2 , v 3 1 x 2 x 2 ,2 5 x x 2 ,x x 2
Sol:
c1v1+c2v2+c3v3 = 0
i.e., c1(1+x – 2x2) + c2(2+5x – x2) + c3(x+x2) = 0+0x+0x2
c1+2c2
=0
c1+5c2+c3 = 0
–2c1– c2+c3 = 0
1 2
1 2 0 0
G. E.
1 5 1 0
0 1
2 1 1 0
0 0
0 0
1 0
3
0 0
This system has infinitely many solutions
(i.e., this system has nontrivial solutions, e.g., c1=2, c2= – 1, c3=3)
S is (or v1, v2, v3 are) linearly dependent
11. Basis
• Basis :Basis
V: a vector space
S ={v1, v2, …, vn}
S is linearly independent
(For ci vi = Ax 0, there is only the trivial solution (det(A) 0),
- S is called a basis for V
12.
Ex1: the standard basis vectors in R3:13.
Ex 2: The nonstandard basis for R2Show that S ={v1 ,v 2 }={(1,1), (1, 1)} is a basis for R 2
c1 c2 =0
(2) For c1v1 +c2 v 2 =0
c1 c2 =0
Because the coefficient matrix of this system has a nonzero determinant, you
know that the system has only the trivial solution. Thus you can conclude that S is
linearly independent
According to the above two arguments, we can conclude that S
is a (nonstandard) basis for R2
14.
15.
16.
17.
18.
19. Applications of vectors
• https://www.machinelearningplus.com/nlp/cosine-similarity/
• http://www.cs.utoronto.ca/~strider/d18/Lin
Alg.pdf


















 Математика
Математика








