Похожие презентации:
Векторы и матрицы
1.
ВЕКТОРЫ И МАТРИЦЫВектор
С упорядоченной последовательностью действительных
чисел a1,a2,a3,…,an-1,an можно связать понятие связанного
вектора в n-мерном пространстве и обозначить как:
a1
a
2
a a .
.
a n
или понятие точки A(a1,a2,a3,…,an).
Числа a1,a2,a3,…,an называются элементами(проекциями) вектора a или
координатами точки A, а количество элементов в векторе называется
размерностью этого вектора. Положение элемента ai определяется индексом i,
где i = 1,2,· ··,n. Элементы вектора записываются в виде столбца.
1
2.
Типы векторовНулевой – вектор, все компоненты которого равны
нулю и обозначается как:
Единичный – вектор, длина которого
равна единице:
0
a 0
0
a=[0;0;0];
a= zeros(3,1);
0 .6
a ; 0.6 2 0.82 1 a= [0.6; 0.8];
0 .8
a1
Транспонированный - вектор, который
a a 2 a T a1 a 2 a 3
представлен строкой.
a n
at= a’;
2
3.
МатрицаСовокупность чисел
расположенных в прямоугольной
таблице, состоящей из n строк и
m столбцов, называется
матрицей и обозначается как:
a11 a12 a13 a1m
a
a
a
a
23
2m
A A 21 22
a
n1 a n 2 a n 3 a nm
Положение элемента a ij в матрице определяется двумя индексами (i и j),
где i определяет номер строки , а j – номер столбца .
3
4.
Типы матрицМатрица, состоящая из одной строки
называется вектор строка n=1
A=[1 2 3]; или A=[1:3]
С =[1 3 5 7 9]; или C=[1:2:9];
Матрица, состоящая из одного столбца
называется вектор столбец m=1
A=[1;2;3];
Если n равно m матрица называется квадратной
A=[1 2 3;4 3 2;0 1 3];
Верхне треугольная aij=0 при i>j
A=[1 2 3;0 2 3;0 0 4];
Нижне треугольная
aij=0 при i<j
A=[1 0 0;2 3 0;1 2 3];
Диагональная
a ij 0 при i j
A=[3 0 0;0 2 0; 0 0 5];
Единичная
1 при i j
eij
0 при i j
E=[1 0 0;0 1 0;0 0 1];
E=eye(3);
Транспонированная
матрица в которой строки заменены
на соответствующие столбцы
AT=A’;
a tj,i a i, j , где i 1,2,3,..., n; j 1,2,3,..., m
Равенство матриц
A B т.е. aij= bij
где i=1,2,3,…,n
j=1,2,3,…,m
4
5.
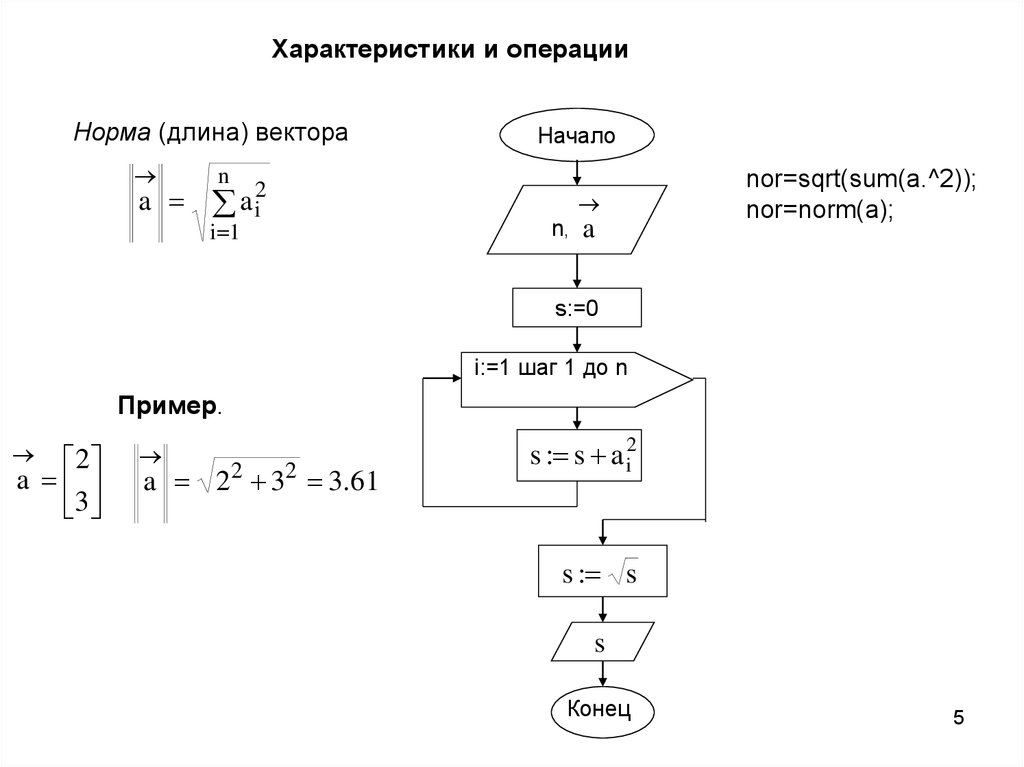
Характеристики и операцииНорма (длина) вектора
a
Начало
n
a i2
i 1
n,
a
nor=sqrt(sum(a.^2));
nor=norm(a);
s:=0
i:=1 шаг 1 до n
Пример.
2
a
3
a 2 2 32 3.61
s : s a i2
s : s
s
Конец
5
6.
файл сценарияclc
n=input('n=');
a=inpVec(n,’a’);
disp(nVec(n,a));
Файл функция
Файл функция
function vec=inpVec(n,nameVec);
for i=1:n
vec(i,1)=input(sprintf('%s(%g)=',nameVec,i));
end
function nor=nVec(n,a);
s=0;
for i=1:n
s=s+a(i)^2;
end
nor=sqrt(s);
6
7.
Норма матрицы(Эвклидова).
A
n m
Nor_A=sqrt(sum(A.^2));
Nor_A=norm(A,’fro’);
a i2, j
i 1 j 1
файл сценария
Файл функция
clc
n=input('n=');
m=input(‘m=‘);
A= inpMatr(n,m,’A’);
Nor_A=nMatr(n,m,A);
disp(Nor_A);
disp(norm(A,'fro'));
function nor=nMatr(n,m,A);
s=0;
for i=1:n
for j=1:m
s=s+A(i,j)^2;
end
end
nor=sqrt(s);
Файл функция
function matr=inpMatr(n,m,nameMatr);
for i=1:n
for j=1:m
matr(i,j)=input(sprintf('%s(%g,%g)=',nameMatr,i,j));
end
end
7
8.
Сложение и вычитание векторов.Складывать или вычитать можно только вектора с одинаковой размерностью.
c a b
ci a i bi , i 1,2,3,.., n
файл сценария
clc
n=input('n=');
a=inpVec(n,'a');
b=inpVec(n,'b');
c=addVec(n,a,b);
disp(' c'); disp(c)
Файл функция
function vec=addVec(n,a,b);
for i=1:n
vec(i)=a(i)+b(i);
end
c=a+b;
9.
Сложение и вычитание матриц.Складывать или вычитать можно только матрицы с одинаковой
размерностью.
C=A+B;
C A B; cij a ij bij , i 1,2,3,..., n; j 1,2,3,..., m
файл сценария
n=input('n=');
m=input('n=');
A= inpMatr(n,m,’A’);
B= inpMatr(n,m,’B’);
C= addMatr(n,m,A,B);
disp(‘
C’); disp(C);
Файл функция
function matr=addMatr(n,m,A,B);
for i=1:n
for j=1,m
matr(i,j)=A(i,j)+B(i,j)
end
end
9
10.
Умножение вектора на константу.c a
ci a i , i 1,2,3,..., n
c=λ*b;
Умножение матрицы на константу.
C A; ci, j a i, j
i 1,2,3,..., n; j 1,2,3,..., m
C= λ *B;
Скалярное произведение векторов
Это значение суммы произведений соответствующих компонент двух
векторов.
T
n
z ( a , b ) a b a i bi , i 1,2,3,..., n
2
i 1
z=a’ * b;
4
4
z 2 3 2 4 3 5 23
5
Пример a b
3
5
Файл функция
function sp=scalpr(n,a,b);
sp=0;
for i=1:n
sp=sp+a(i)*b(i);
end
|
|
|sp=sum(a.*b);
|
z=scalpr(n,a,b);
10
11.
Угол между векторами.Косинус угла
cos( )
Ортогональность векторов
T
a b
r=a’*b/(norm(a)*norm(b))
a b
T
cos( ) 0 т.е. a b 0
Линейная зависимость векторов
(i )
Вектора a называются линейно зависимыми, если соотношение
справедливо, хотя бы при одном множителе
(1)
Пример:
a
i
m
(i )
i a
0
i 1
отличным от нуля.
( 2)
(1)
( 2)
2
1
2
1 0
; a
1 a 2 a
0 1 2
4
2
4
2 0
1 2 2 1 0 2 2 1
1 4 2 2 0 1 4 1 4 0 1 0 0 при любом 1
11
12.
Умножение матриц.C A B B A
Cnm A nk Bkm
Количество столбцов матрицы A должно равняться количеству строк матрицы B
Элемент c ij вычисляется как скалярное произведение i-й строки матрицы A
и j-го столбца матрицы B
k
cij a il b lj
C=A*B;
l 1
Файл функция
function RM=multMatr(n,k,m,A,B);
for i=1:n
for j=1:m
s=0;
for ℓ=1:k
s=s +A(i,ℓ) *B(ℓ,j);
end
RM(i,j)=s;
end
end
|
|
|RM(i,j)=A(i,:)*B(:,j);
|
|
C=multMatr(n,k,m,A,B);
12
13.
AO=inv(A);Обращение матрицы методом Гаусса-Жордана
Обратной матрицей называется такая квадратная матрица
1
A nn
,
при умножении которой на исходную как справа так и слева
1
1
A A A A
получается единичная матрица
E
Обращение матрицы
A
методом Гаусса-Жордана
заключается в построении расширенной матрицы
A E
и преобразовании расширенной матрицы так, чтобы на месте
исходной получилась единичная матрица, тогда на месте единичной
получится обратная матрица:
1
E n n A nn
13
14.
Текстуальный алгоритмметода Гаусса-Жордана состоит из четырёх этапов.
1. Строим расширенную матрицу дописав к исходной квадратной матрице
единичную матрицу того же размера
C n , 2 n A n n E n n , и задаём номер ведущей строки k=1.
2. Делим элементы k-й строки начиная с k-ого на c kk
c kj
c kj
c
c kk , j = k,k+1,k+2,…,2·n т.е. kk =1.
E=eye(n);
C=[A,E];
3. Преобразуем все i-е строки кроме k-й, i=1,2,3,…,n i≠k так, чтобы элементы
cik=0. Для этого из каждого элемента i-й строки начиная с k-ого вычитаем
соответствующий элемент k-й строки, умноженный на элемент cik , т.е.
cij cij ckj cik , j k, k 1, k 2,...,2 n
4. Проверяем условие k<n, если оно справедливо, то k=k+1 и выполняем
алгоритм с пункта 2, иначе выводим полученную обратную матрицу,
расположенную на месте единичной.
14
15.
4.00 1.00 1.00Пример. Найти обратную матрицу. A 2.00 5.50 1.00
2.00 1.00 4.00
4.00 1.00 1.00 1.00 0.00 0.00
C 2.00 5.50 1.00 0.00 1.00 0.00
2.00 1.00 4.00 0.00 0.00 1.00
1.00 0.25 0.25 0.25
2.00 5.50 1.00 0.00
2.00 1.00 4.00 0.00
0.00
1.00
0.00
0.00
0.00
1.00
1.00 0.25 0.25 0.25 0.00 0.00
0.00 5.00 0.50 0.50 1.00 0.00
0.00 0.50 3.50 0.50 0.00 1.00
k=1
Делим все элементы 1ой строки на
c1,1(4.00)
i=2 – из 2ой строки вычитаем 1ую
умноженную на c21(2.00)
i=3 – из 3ей строки вычитаем 1ую
умноженную на c31(2.00)
k=2
Делим все элементы 2ой строки
на c2,2(5.00)
15
16.
0.25 0.00 0.001.00 0.25 0.25
0.00 1.00 0.10 0.10 0.20 0.00
0.00 0.50 3.50 0.50 0.00 1.00
1.00 0.00 0.23 0.28 0.05 0.00
0.00 1.00 0.10 0.10
0.20 0.00
0.00 0.00 3.45 0.45 0.10 1.00
1.00 0.00 0.23 0.28 0.05 0.00
0.00 1.00 0.10 0.10
0.20 0.00
0.00 0.00 1.00 0.13 0.03 0.29
i=1 – из 1ой строки вычитаем 2ую
умноженную на c12(0.25)
i=3 – из 3ей строки вычитаем 2ую
умноженную на c32(0.50)
k=3
Делим все элементы 3ей строки
на c33(3.45)
i=1 – из 1ой строки вычитаем 3ью
умноженную на c13(0.23)
i=2 – из 2ой строки вычитаем 3ью
умноженную на c23(0.10)
1.00 0.00 0.00 0.30 0.04 0.07
0.00 1.00 0.00 0.09
0.20 0.03
0.00 0.00 1.00 0.13 0.03
0.29
1
A
0.30 0.04 0.07
0.09 0.20 0.03
0.13 0.03 0.29
16















 Математика
Математика Программирование
Программирование








