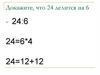Метод математической индукции

1. Метод математической индукции

презентацию выполнили
ученики(-цы) 9 класса "Б"
МАОУ "Средняя Общеобразовательная Школа №83"
Рыбалко Екатерина, Дудырев Артём, Ямшинина Ульяна
город Пермь, 2019 год

2. Цели / Задачи проекта

обозначить
определение математической индукции
в краткой форме изложить историю возникновения метода
математической индукции
изложить формулировку принципа математической индукции
представить составляющее метода математической индукции
привести примеры и разобрать их, используя данный метод

3. Определение математической индукции

Математическая индукция — метод математического доказательства,
который используется для доказательства истинности некоторого
утверждения для всех натуральных чисел.

4. История появления метода математической индукции К середине XVII века в математике накопилось немало ошибочных выводов в силу

того, что многие
ученные верили в непогрешимость индукции. Требовалось научное обоснование метода, который
позволял бы делать общие выводы на основании рассмотрения нескольких частных случаев. И такой
метод был разработан. Основная заслуга в этом принадлежит французским математикам Паскалю и
Декарту, а также швейцарскому математику Бернулли, хоть и отдельные случаи применения
встречаются ещё в античные времена у Эвклида.

5. Принцип математической индукции

Если свойство, зависящее от натурального n, во-первых, верно при n=1 и,
во-вторых, из предположения, что оно верно при n=k, следует, что оно
верно при n=k+1, то считают что это свойство верно для любого
натурального n.

6. Составляющее метода математической индукции

Для справедливости любого утверждения, высказанного для всех
натуральных чисел n>1, достаточно:
(1) Доказать данное утверждение для n=1.
(2) Предположить его справедливость при n=k≥1.
(3) Доказать, что оно n=k+1.

7. Разбор примеров доказательств утверждений с помощью метода математической индукции

I. Применение метода математической индукции к доказательству 0 n=0.
II. Применение метода математической индукции к доказательству
неравенств.
III. Применение метода математической индукции к доказательству
формулы суммы первых n членов геометрической прогрессии, где q≠1.