Алгоритм решения системы уравнений графическим способом

1. Алгоритм решения системы уравнений графическим способом

1. Приводим оба уравнения к виду
линейной функции y = k x + m.
2. Составляем расчётные таблицы для
каждой функции.
3. Строим графики функций в одной
координатной плоскости.
4. Определяем координаты точки
пересечения прямых, делаем
проверку!
5. Записываем ответ.

2.

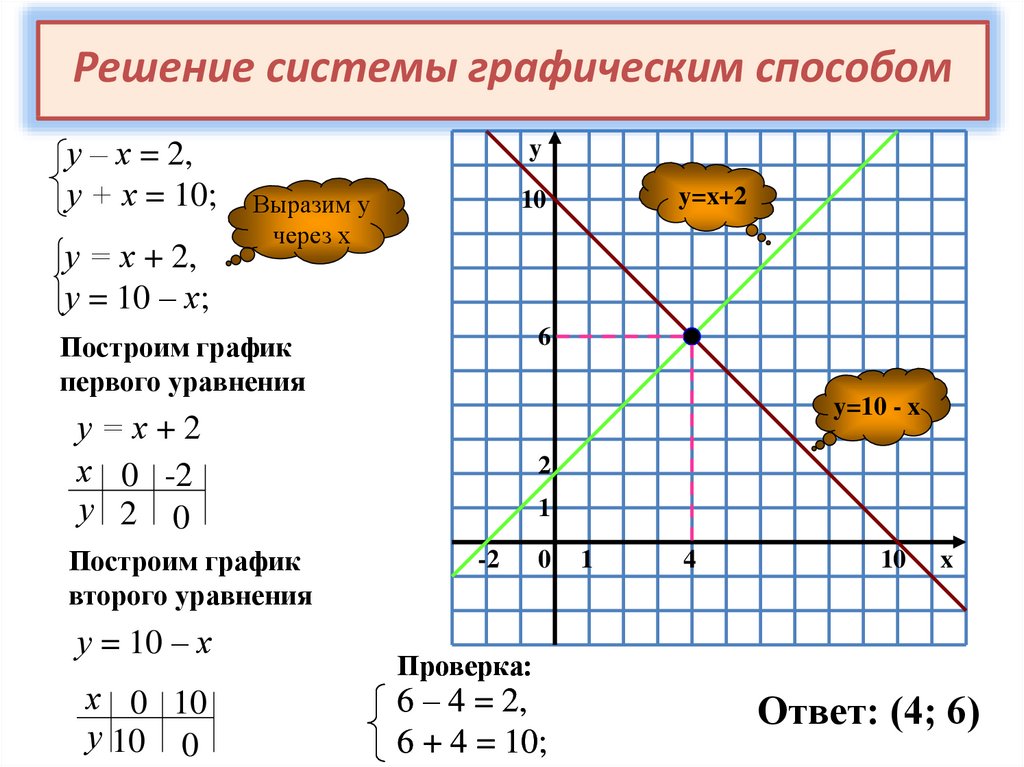
Решение системы графическим способом
у – х = 2,
у + х = 10;
у = х + 2,
у = 10 – х;
y
Выразим у
через х
6
Построим график
первого уравнения
y=10 - x
у=х+2
х 0 -2
у 2 0
Построим график
второго уравнения
у = 10 – х
х 0 10
у 10 0
y=x+2
10
2
1
-2
0
1
4
10
x
Проверка:
6 – 4 = 2,
6 + 4 = 10;
Ответ: (4; 6)

3. Графический метод решения системы x + y = 3 y – 2x = – 3

Графический метод решения системы
у =3–x
x
y
0
3
3
0
A(0;3)
у = 2x – 3
x
y
0
–3
3
3
D(3;3)
M(2;1)
у =1
B(3;0)
X=2
C(0; – 3)
Проверка:
2 + 1 = 3,
1 – 2 2 = -3;
x+y=3
y – 2x = – 3
Ответ: (2; 1)

4.

Частный случай решения системы уравнений
Y=0,5x+2
x y
0
2
2
3
B(2;3)
A(0;2)
D(2;0)
Y=0,5x-1
y
x
0 -1
2 0
C(0;-1)
Решим систему уравнений:
Y= 0,5x+2
Y= 0,5x-1
Графики функций
параллельны и не
пересекаются.
Говорят, что система
несовместная.
Ответ: Система не имеет решений.

5.

Частный случай решения системы уравнений
у=x+3
x
y
0
3
-3
0
D(1;4)
A(0;3)
C(-1;2)
Решить систему:
2у=2x+6
-x + у – 3 = 0
Выразим у:
у=x+3
B(-3;0)
у=x+3
x
y
1
4
-1
2
у = х+3
Графики функций
совпадают.
Говорят, что система
неопределённая
Ответ: система имеет бесконечное множество решений

6. Если система уравнений не имеет решений, то она называется несовместной. Если система уравнений имеет бесконечно много решений,

Достоинство
графического
способа –
наглядность.
Недостаток
графического
способа–не всегда
легко определить
точные значения
переменных,
нужна проверка.
Если система
уравнений не
имеет решений, то
она называется
несовместной.
Если система
уравнений имеет
бесконечно много
решений, то она
называется
неопределённой.