Похожие презентации:
Сферическое движение твердого тела движение свободного твердого тела
1. § 4 СФЕРИЧЕСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА
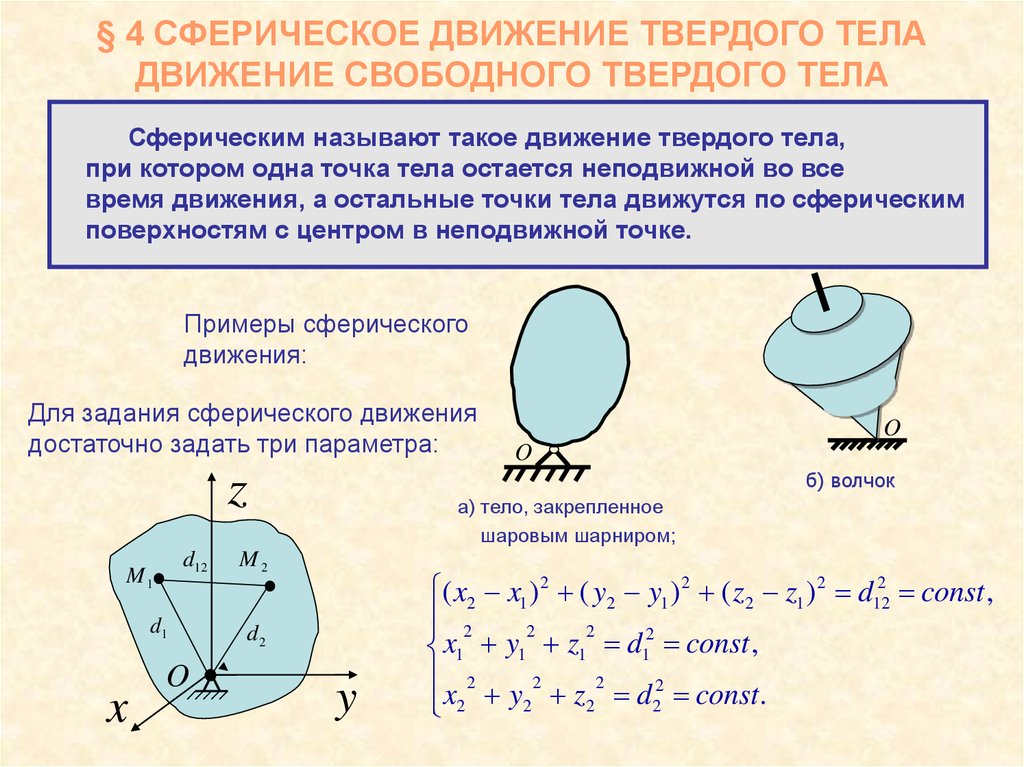
Сферическим называют такое движение твердого тела,при котором одна точка тела остается неподвижной во все
время движения, а остальные точки тела движутся по сферическим
поверхностям с центром в неподвижной точке.
Примеры сферического
движения:
Для задания сферического движения
достаточно задать три параметра:
а) тело, закрепленное
шаровым шарниром;
d12
d1
x
O
O
б) волчок
z
M1
O
M2
d2
y
( x2 x1 ) 2 ( y2 y1 ) 2 ( z2 z1 ) 2 d122 const ,
2
2
2
2
x
y
z
1
1
1 d1 const ,
2
2
2
2
x
y
z
2
2
2 d 2 const .
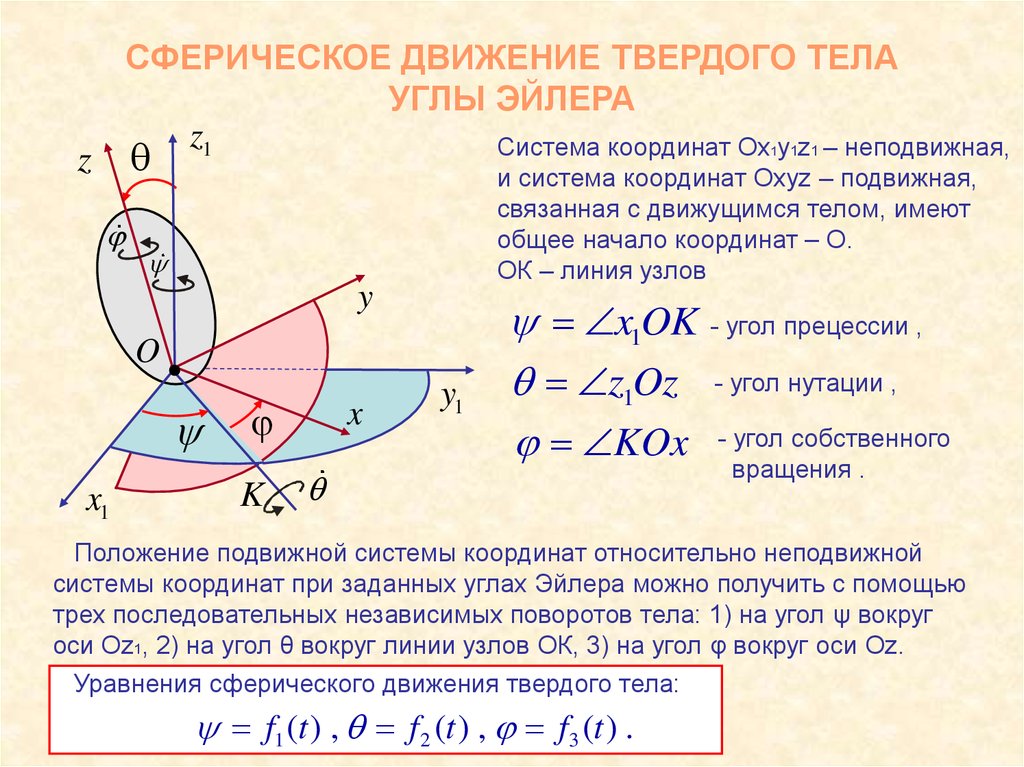
2. СФЕРИЧЕСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА УГЛЫ ЭЙЛЕРА
z1Система координат Ox y1z1 – неподвижная,
z
1
и система координат Oxyz – подвижная,
связанная с движущимся телом, имеют
общее начало координат – О.
ОК – линия узлов
y
O
x1
K
x
y1
x1OK - угол прецессии ,
z1Oz - угол нутации ,
KOx - угол собственного
вращения .
Положение подвижной системы координат относительно неподвижной
системы координат при заданных углах Эйлера можно получить с помощью
трех последовательных независимых поворотов тела: 1) на угол ψ вокруг
оси Oz1, 2) на угол θ вокруг линии узлов ОК, 3) на угол φ вокруг оси Oz.
Уравнения сферического движения твердого тела:
f1 (t ) , f 2 (t ) , f3 (t ) .
3. ТЕОРЕМА ЭЙЛЕРА - ДАЛАМБЕРА
Всякое перемещение твердого тела около неподвижной точки можноосуществить с помощью одного только поворота этого тела вокруг
определенной оси, проходящей через неподвижную точку и называемой
осью конечного поворота
Движение твердого тела около неподвижной точки можно
рассматривать как непрерывную последовательность
элементарных перемещений, каждое из которых в силу
теоремы Эйлера-Даламбера можно осуществить одним
только поворотом на бесконечно малый угол вокруг
некоторой оси, проходящей через неподвижную точку –
мгновенной оси вращения.
Таким образом, сферическое движение твердого тела
можно рассматривать как непрерывную последовательность
бесконечно малых поворотов тела вокруг мгновенных
осей вращения, проходящих через неподвижную точку.
О1
.
A
О
B
C
D
A1
B1
Геометрическое место мгновенных осей вращения тела в
пространстве, связанном с неподвижной системой отсчета,
образует коническую поверхность – НЕПОДВИЖНЫЙ
АКСОИД, а в подвижном пространстве, связанном с
движущимся телом - коническую поверхность – ПОДВИЖНЫЙ
АКСОИД. Неподвижная точка О при этом является общей
вершиной для неподвижного и подвижного аксоидов, а их
общая образующая – мгновенной осью вращения тела.
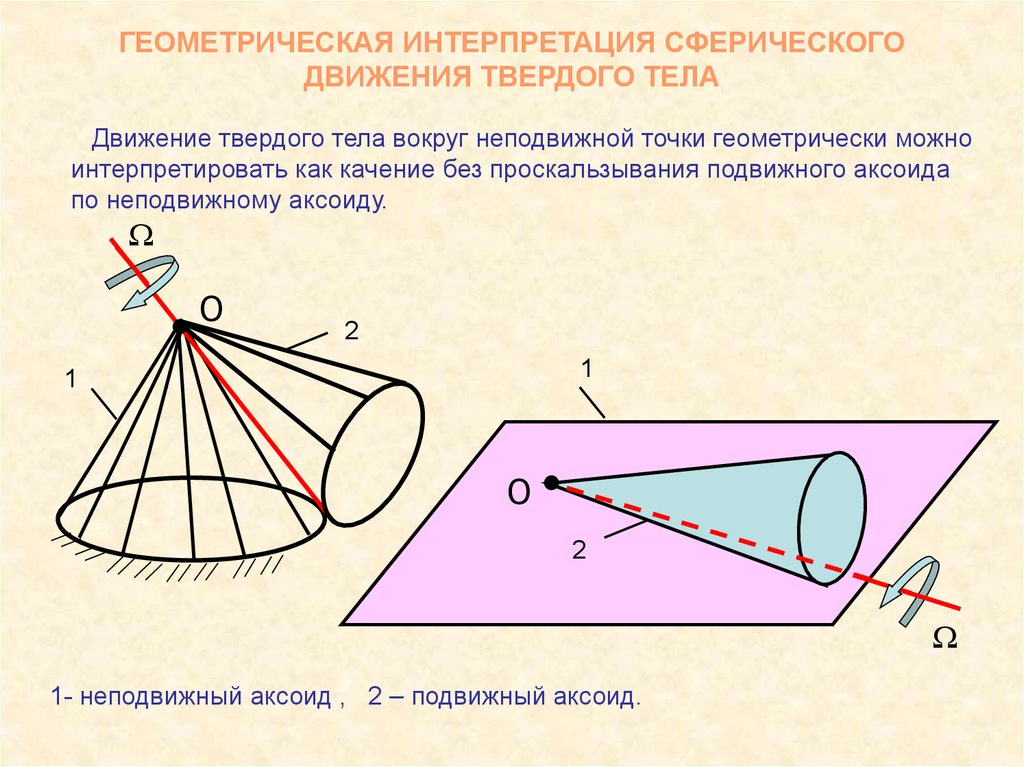
4. ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ СФЕРИЧЕСКОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Движение твердого тела вокруг неподвижной точки геометрически можноинтерпретировать как качение без проскальзывания подвижного аксоида
по неподвижному аксоиду.
.
O
2
1
1
O
.
2
1- неподвижный аксоид , 2 – подвижный аксоид.
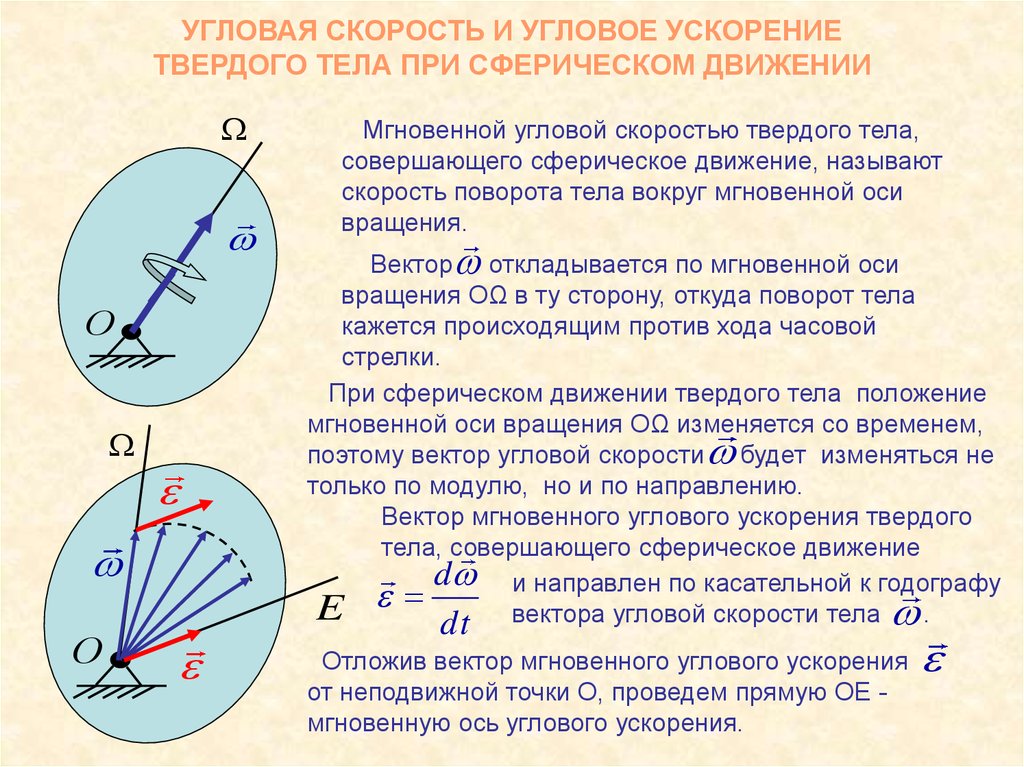
5. УГЛОВАЯ СКОРОСТЬ И УГЛОВОЕ УСКОРЕНИЕ ТВЕРДОГО ТЕЛА ПРИ СФЕРИЧЕСКОМ ДВИЖЕНИИ
ОО
Мгновенной угловой скоростью твердого тела,
совершающего сферическое движение, называют
скорость поворота тела вокруг мгновенной оси
вращения.
Вектор откладывается по мгновенной оси
вращения ОΩ в ту сторону, откуда поворот тела
кажется происходящим против хода часовой
стрелки.
При сферическом движении твердого тела положение
мгновенной оси вращения ОΩ изменяется со временем,
поэтому вектор угловой скорости будет изменяться не
только по модулю, но и по направлению.
Вектор мгновенного углового ускорения твердого
тела, совершающего сферическое движение
d и направлен по касательной к годографу
E dt вектора угловой скорости тела .
Отложив вектор мгновенного углового ускорения
от неподвижной точки О, проведем прямую ОЕ мгновенную ось углового ускорения.
6. ВЫЧИСЛЕНИЕ УГЛОВОГО УСКОРЕНИЯ
1) Пусть известны проекции вектора мгновенной угловой скорости твердоготела на подвижные или неподвижные оси координат ( x , y , z ),тогда
проекции вектора мгновенного углового ускорения на те же оси находятся
путем дифференцирования по времени соответствующих проекций:
При этом модуль и направление вектора
d x
d x
d x мгновенного углового ускорения твердого тела
x
, x
, x
.
dt
dt
dt определяются по формулам:
x2 y2 z2 ,
cos( x) x ,
cos(
y) y ,
cos(
z) z .
e
О
E
2) Пусть
const.
Тогда
d
e ,
dt
где
- угловая скорость вращения мгновенной оси
e
вращения тела, по которой направлен вектор
мгновенной угловой скорости.
При этом e sin .
7. СКОРОСТИ ТОЧЕК ТВЕРДОГО ТЕЛА, СОВЕРШАЮЩЕГО СФЕРИЧЕСКОЕ ДВИЖЕНИЕ
Скорости точек твердого тела, совершающего сферическое движение, в каждыймомент времени определяются как скорости во вращении этих точек вокруг
мгновенной оси вращения тела ОΩ. При этом скорости точек тела, лежащих на
мгновенной оси вращения равны нулю.
dr
V
r - формула Эйлера.
dt
V r r sin h .
z1
i
h
V
M
r
k
V r x y z i ( y z z y )
x
y
z
j ( z x x z ) k ( x y y x).
O
y1
x1
j
Проекции вектора скорости точки на неподвижные (или
подвижные) оси координат выражаются формулами:
Vx ( y z z y),Vy ( z x x z),Vz ( x y y x).
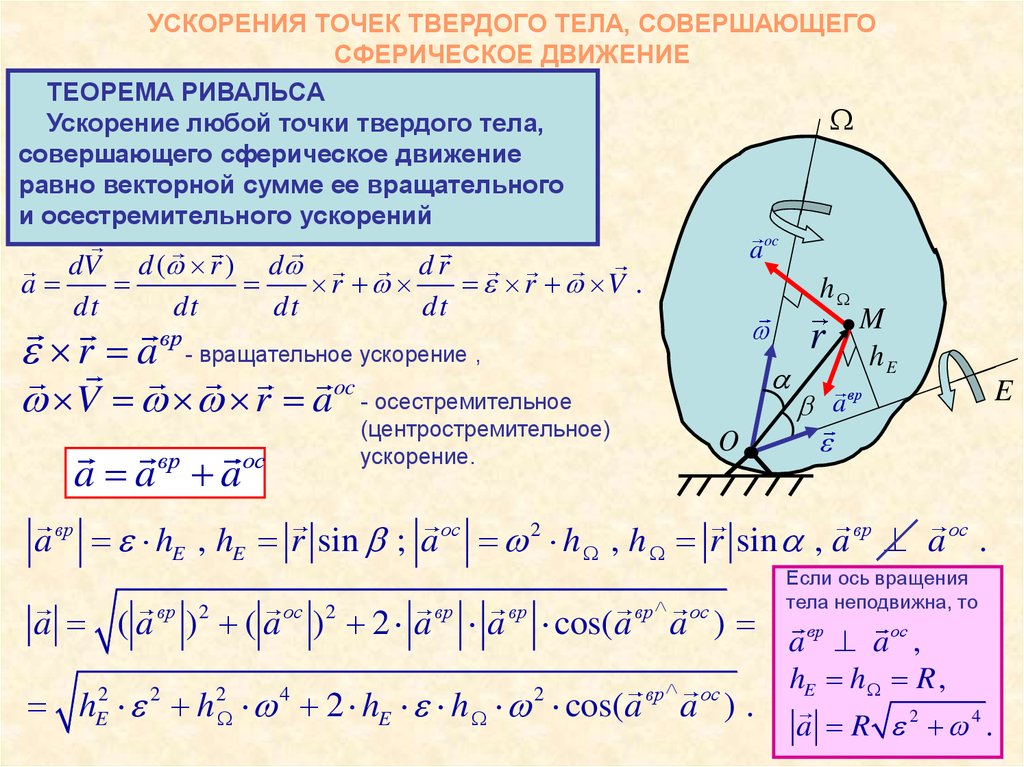
8. УСКОРЕНИЯ ТОЧЕК ТВЕРДОГО ТЕЛА, СОВЕРШАЮЩЕГО СФЕРИЧЕСКОЕ ДВИЖЕНИЕ
ТЕОРЕМА РИВАЛЬСАУскорение любой точки твердого тела,
совершающего сферическое движение
равно векторной сумме ее вращательного
и осестремительного ускорений
a oc
a
dV d ( r ) d
dr
r
r V .
dt
dt
dt
dt
h
r a - вращательное ускорение ,
V r a oc - осестремительное
вр
a a a
вр
(центростремительное)
ускорение.
oc
O
r
M
hE
вр
a
a вр hE , hE r sin ; a oc 2 h , h r sin , a вр a oc .
a ( a ) ( a ) 2 a
вр
oc
2
2
вр
a
вр
cos(a
вр
h h 2 hE h cos(a
2
E
2
2
4
2
Если ось вращения
тела неподвижна, то
a oc ) a вр a oc ,
вр
oc
a ).
hE h R ,
a R 2 4 .
E
9. ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА
.B1
ƖƖ
.
z2
.
C1
z
z1
C'
B.
.B
'
C
Ɩ
y
O
.A
.
1
.A
O
x1
x
K
zA
yA
x2
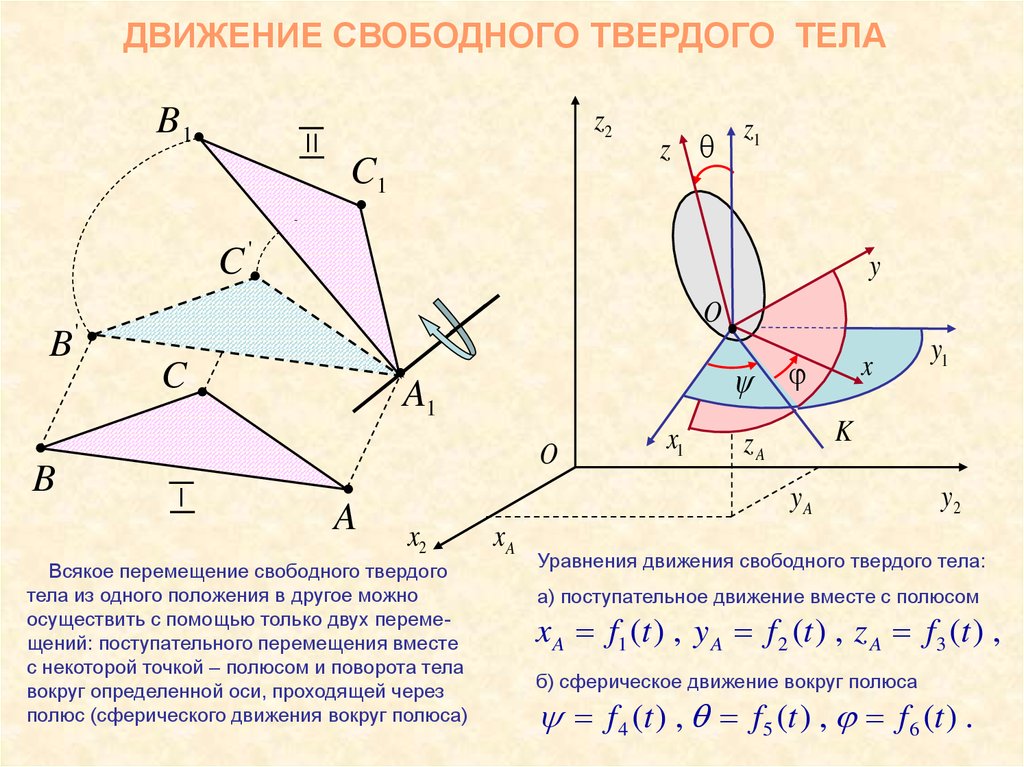
Всякое перемещение свободного твердого
тела из одного положения в другое можно
осуществить с помощью только двух перемещений: поступательного перемещения вместе
с некоторой точкой – полюсом и поворота тела
вокруг определенной оси, проходящей через
полюс (сферического движения вокруг полюса)
xA
y1
y2
Уравнения движения свободного твердого тела:
а) поступательное движение вместе с полюсом
x A f1 (t ) , y A f 2 (t ) , z A f 3 (t ) ,
б) сферическое движение вокруг полюса
f 4 (t ) , f5 (t ) , f 6 (t ) .
10. ТЕОРЕМА О СКОРОСТЯХ ТОЧЕК СВОБОДНОГО ТВЕРДОГО ТЕЛА
Скорость любой точки свободного твердого тела равна векторной суммескорости полюса и скорости в сферическом движении точки вокруг полюса
z1
Доказательство.
.
VO
M
VMO
O1
x1
.
h
V r
.
O
VO
O
y1
t 0 , O r
тогда
d d O d r
V
, где
dt
dt
dt
d O
VO - скорость полюса О ;
dt
dr
r VMO
dt
V VO VMO
скорость точки М
в сферическом
движении вокруг
полюса О.
Следствия.
1) Проекции векторов скоростей точек свободного твердого тела на прямую, соединяющую эти точки
равны (см. теорема Грасгофа);
2) Концы векторов скоростей точек свободного твердого тела, лежащих на одном, отрезке лежат на одной
прямой и делят ее в том же отношении, в каком сами точки делят отрезок;
3) Скорости точек свободного тела, лежащих на прямой, параллельной мгновенной оси вращения тела,
геометрически равны.
11. ТЕОРЕМА ОБ УСКОРЕНИЯХ ТОЧЕК СВОБОДНОГО ТВЕРДОГО ТЕЛА
Ускорение любой точки свободного твердого тела равно векторнойсумме ускорения полюса и вращательного и осестремительного ускорений
точки, определенных относительно мгновенной оси вращения и оси
мгновенного ускорений, проходящих через полюс
Доказательство.
На основании теоремы о скорости точки свободного твердого тела:
тогда
V VO r
dV dVO d
dr
a
r
,
dt
dt
dt
dt
где
dVO
d
вр
aO ускорение полюса – О;
r r aMO
dt
dt
- вращательное
ускорение точки М относительно оси мгновенного углового ускорения ОЕ;
dr
ос
VMO r aMO
dt
- осестремительное ускорение
точки М относительно мгновенной оси вращения ОΩ;
вр
ос
a aO aMO
aMO





 Физика
Физика








