Похожие презентации:
Система параллельных сил. Момент силы
1. СИСТЕМА ПАРАЛЛЕЛЬНЫХ СИЛ. МОМЕНТ СИЛЫ
ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ.СТАТИКА
ЛЕКЦИЯ 3
2. НА ПРЕДЫДУЩЕЙ ЛЕКЦИИ
Научитьсязаменять равнодействующей параллельные силы,
определять момент силы относительно точки и
оси
2
Цель лекции
3. СЛОЖЕНИЕ ДВУХ СОНАПРАВЛЕННЫХ СИЛ
Имеет ли такая система сил равнодействующую?(F , F ') ~ (F , F ', Q, Q') ~ (R1, R2 ) ~ R
С
D
A
B
Q Q'
R1 F Q,
R2 F ' Q'
R R1 R2 F Q F ' Q' F F '
R F F'
3
Система параллельных сил
R F F'
4. СЛОЖЕНИЕ ДВУХ СОНАПРАВЛЕННЫХ СИЛ
Где находится точка приложения равнодействующей?tg AD / CD
tg Q / F
С
D
B
A
AD F '
BD F
4
Система параллельных сил
tg BD / CD
tg Q' / F '
AD / CD Q / F
BD/ CD Q' / F '
AD F Q CD
BD F ' Q' CD
Две сонаправленные силы имеют
равнодействующую,
направленную …
равную по модулю …
ее точка приложения …
5. СЛОЖЕНИЕ ДВУХ ПРОТИВОПОЛОЖНО НАПРАВЛЕННЫХ СИЛ
Имеет ли такая система сил равнодействующую?С
B
A
F1 F2
(F1, F2 ) ~ (F1, F1', R) ~ R
F2 F1' R
R F2 F1
5
Система параллельных сил
F1' F1
R F2 F1
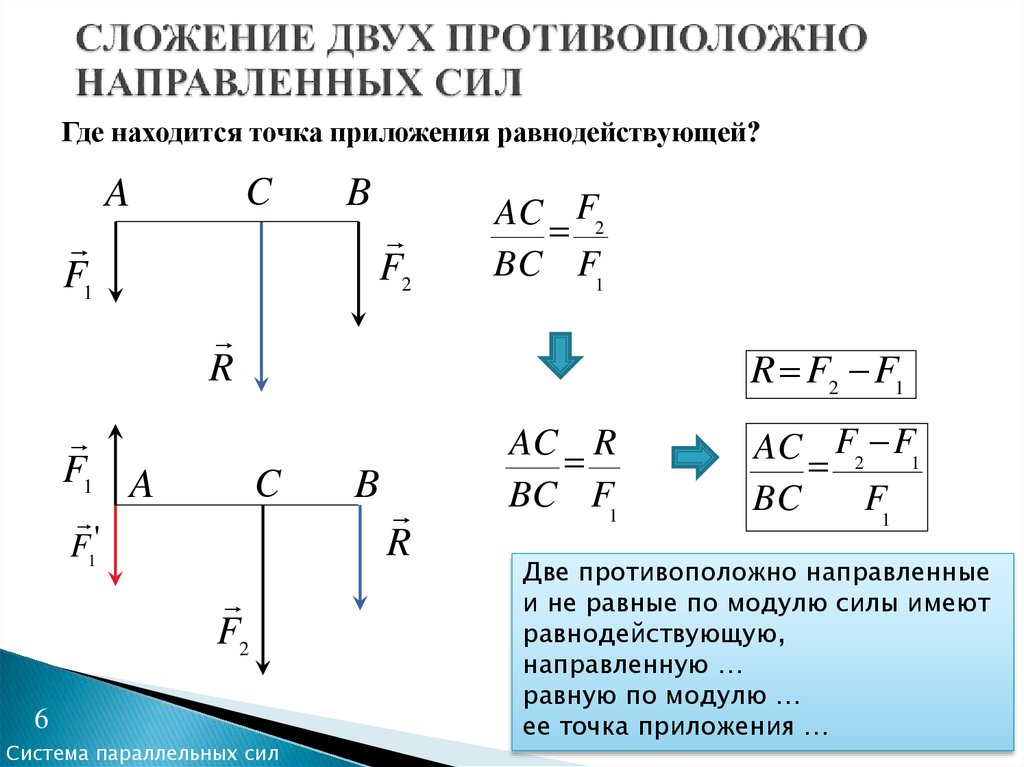
6. СЛОЖЕНИЕ ДВУХ ПРОТИВОПОЛОЖНО НАПРАВЛЕННЫХ СИЛ
Где находится точка приложения равнодействующей?C
A
F1
B
F2
AC F2
BC F1
R
F1 A
R F2 F1
C
F1'
F2
6
Система параллельных сил
B
R
AC R
BC F1
AC F2 F1
BC
F1
Две противоположно направленные
и не равные по модулю силы имеют
равнодействующую,
направленную …
равную по модулю …
ее точка приложения …
7. СЛОЖЕНИЕ ДВУХ ПРОТИВОПОЛОЖНО НАПРАВЛЕННЫХ СИЛ
F2 F1Имеет ли такая система сил равнодействующую?
F1
C
A
F2
7
Система параллельных сил
R F2 F1
R 0
AC F2 F1
BC
F1
BC
Две противоположно направленные
равные по модулю силы не имеют
равнодействующей
8. СЛОЖЕНИЕ ДВУХ ПРОТИВОПОЛОЖНО НАПРАВЛЕННЫХ СИЛ
F1C
A
F2
Две противоположно направленные, равные по модулю силы,
не лежащие на одной прямой, будем называть парой сил
Пара сил, действующая на свободное тело, будет вызывать его
вращение
Мерой вращательного взаимодействия в
механике является момент
8
Система параллельных сил
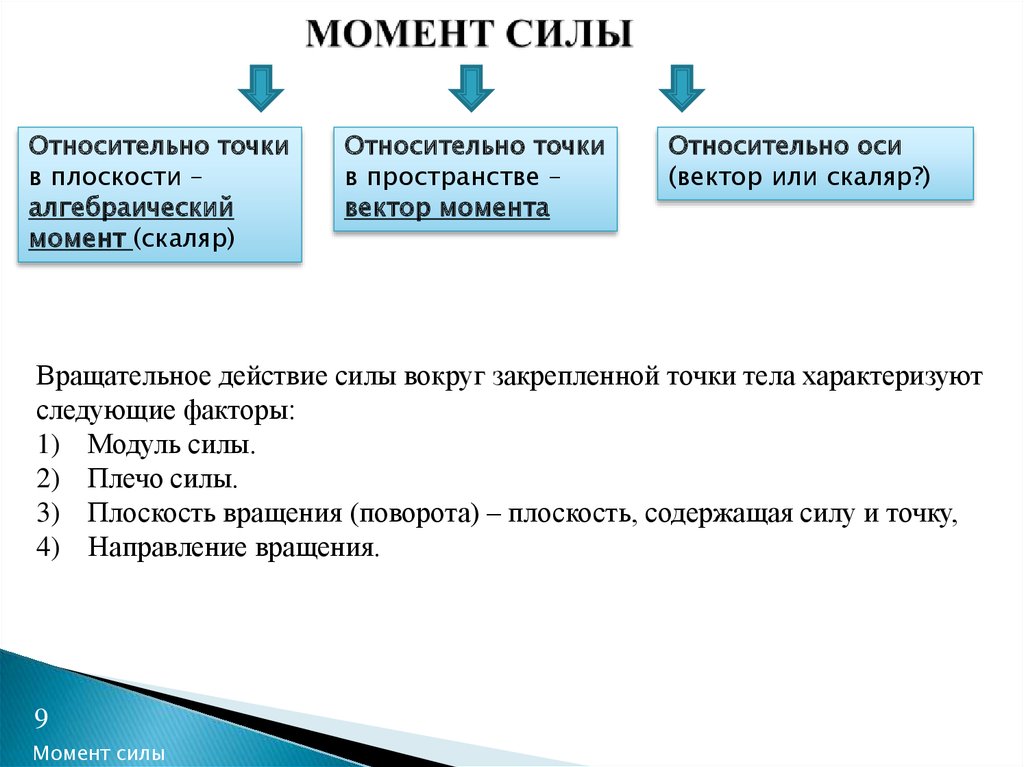
9. МОМЕНТ СИЛЫ
Относительно точкив плоскости –
алгебраический
момент (скаляр)
Относительно точки
в пространстве –
вектор момента
Относительно оси
(вектор или скаляр?)
Вращательное действие силы вокруг закрепленной точки тела характеризуют
следующие факторы:
1) Модуль силы.
2) Плечо силы.
3) Плоскость вращения (поворота) – плоскость, содержащая силу и точку,
4) Направление вращения.
9
Момент силы
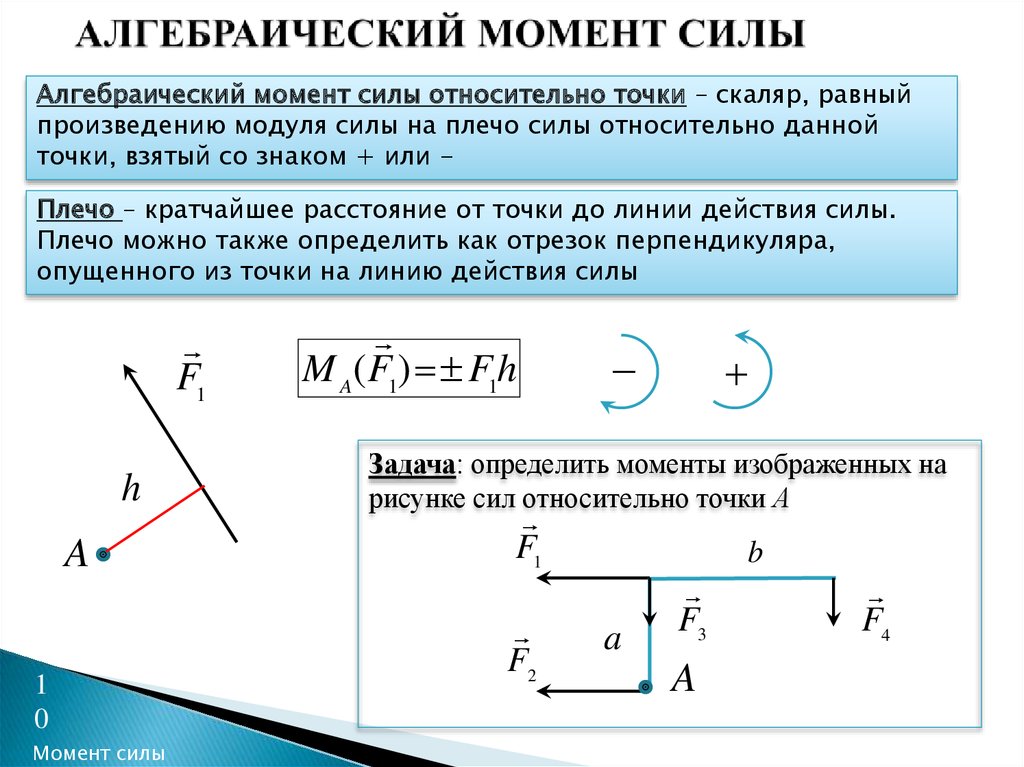
10. АЛГЕБРАИЧЕСКИЙ МОМЕНТ СИЛЫ
Алгебраический момент силы относительно точки – скаляр, равныйпроизведению модуля силы на плечо силы относительно данной
точки, взятый со знаком + или -
Плечо – кратчайшее расстояние от точки до линии действия силы.
Плечо можно также определить как отрезок перпендикуляра,
опущенного из точки на линию действия силы
F1
h
A
1
0
Момент силы
M A(F1) F1h
Задача: определить моменты изображенных на
рисунке сил относительно точки А
F1
F2
b
a
F3
A
F4
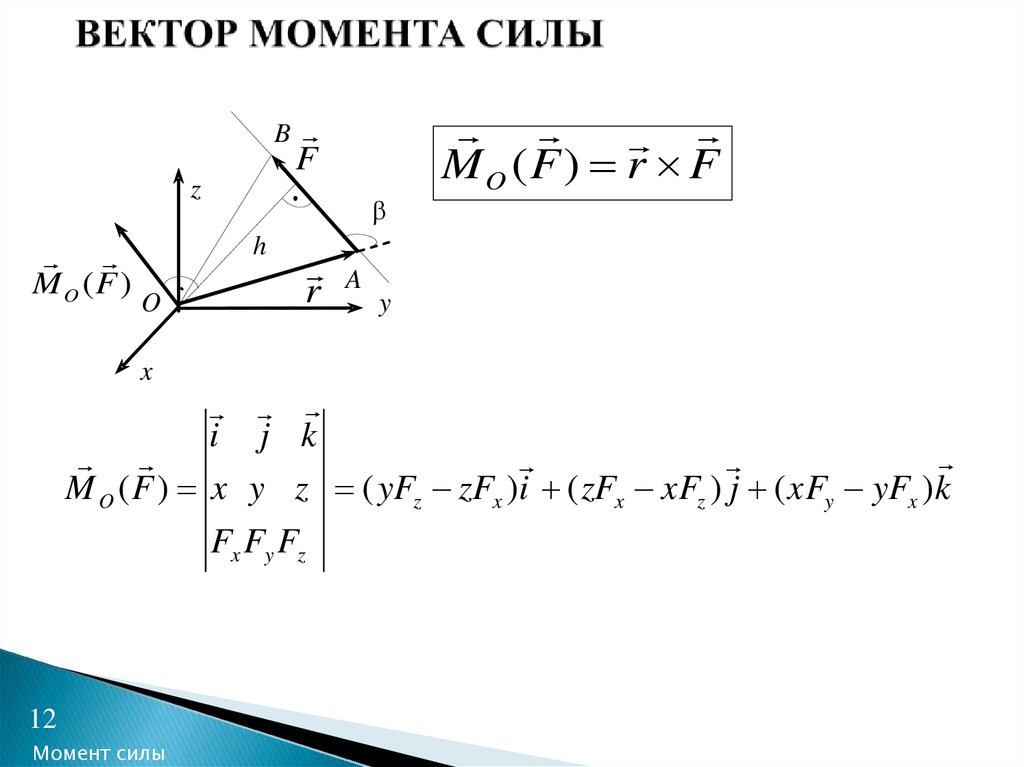
11. ВЕКТОР МОМЕНТА СИЛЫ
Вектор момента силы относительно точки – вектор, равный помодулю произведению модуля силы на плечо относительно данной
точки, и направленный перпендикулярно плоскости, в которой
расположены точка и линия действия силы, в ту сторону, откуда
вращение под действием силы видно происходящим против часовой
стрелки
B
F
z
M O (F )
h
O
x
11
Момент силы
r
A
M O (F ) r F
M O ( F ) r F F r sin F h
y
M O ( F ) F h 2S OAB
12. ВЕКТОР МОМЕНТА СИЛЫ
BF
z
M O (F )
h
O
r
A
M O (F ) r F
y
x
i j k
M O ( F ) x y z ( yFz zFx )i ( zFx xFz ) j ( xFy yFx )k
Fx Fy Fz
12
Момент силы
13. ТЕОРЕМА ВАРИНЬОНА
Векторное произведение удовлетворяет законудистрибутивности:
r ( F1 F2 Fn ) r F1 r F2 r Fn
Теорема Вариньона (для ССС): момент
равнодействующей системы сходящихся сил
относительно произвольной точки (центра)
равен векторной сумме моментов сил
системы относительно того же центра.
1654-1722
M O ( R) rA ( F1 F2 Fn )
13
Момент силы
M O ( Fk )
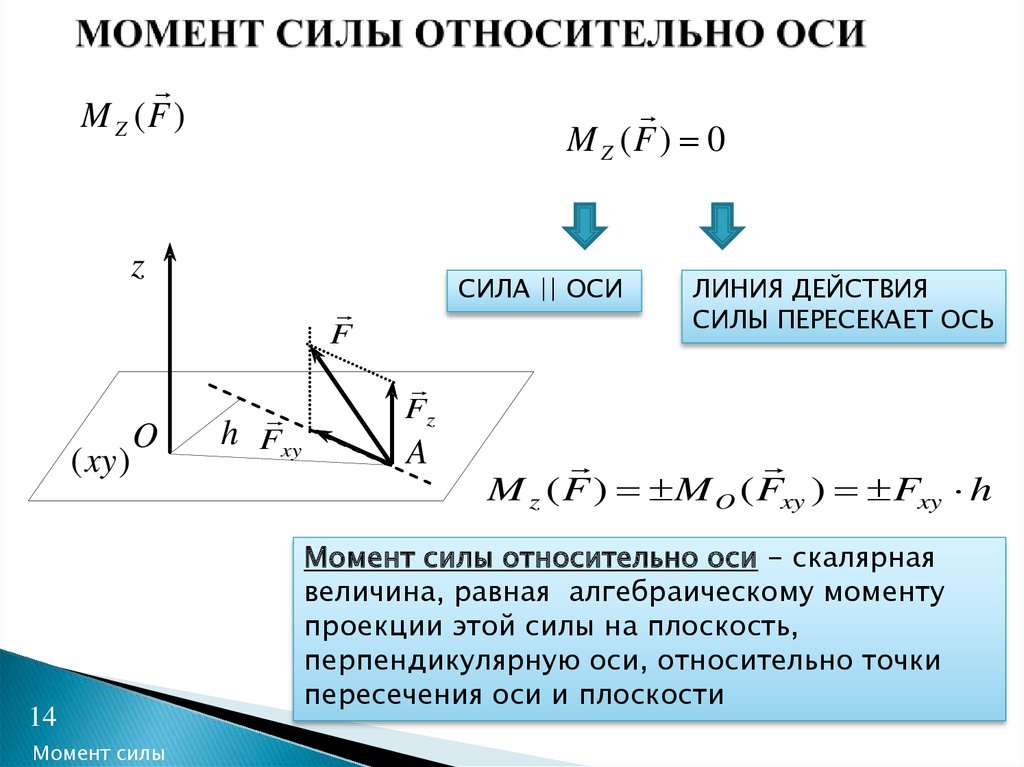
14. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ
M Z (F )M Z (F ) 0
z
СИЛА || ОСИ
F
( xy )
O
14
Момент силы
h Fxy
ЛИНИЯ ДЕЙСТВИЯ
СИЛЫ ПЕРЕСЕКАЕТ ОСЬ
Fz
A
M z ( F ) M O ( Fxy ) Fxy h
Момент силы относительно оси - скалярная
величина, равная алгебраическому моменту
проекции этой силы на плоскость,
перпендикулярную оси, относительно точки
пересечения оси и плоскости
15. ТЕОРЕМА О СВЯЗИ МОМЕНТОВ
Моменты сил относительно осей в системе координат Oxyzравны проекциям момента силы относительно начала
координат О
Если воспользоваться теоремой Вариньона и вычислить момент силы,
разложив ее на составляющие, получим
z
F
.
O
x
15
Fx
y
M Z ( F ) ( xFy yFx )
Fy
Fxy
i j k
M O ( F ) x y z ( yFz zFx )i ( zFx xFz ) j ( xFy yFx )
Fx Fy Fz
( xFy yFx )k
Момент силы









 Физика
Физика








