Похожие презентации:
Модели экспоненциального сглаживания. Тема 2
1.
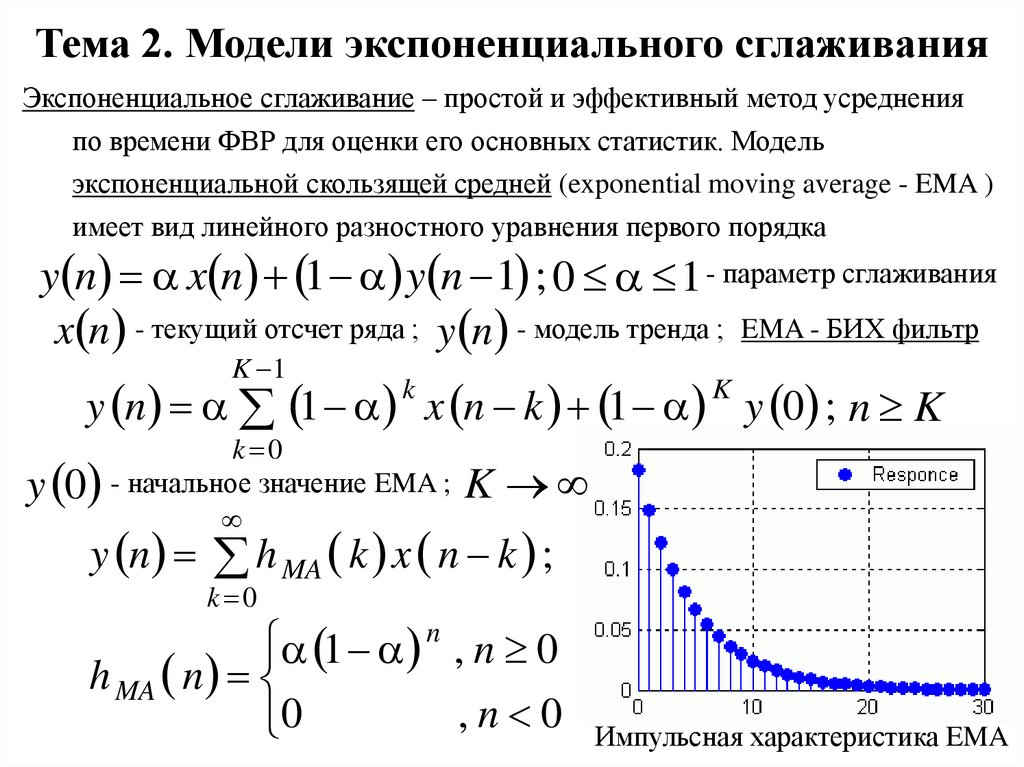
Тема 2. Модели экспоненциального сглаживанияЭкспоненциальное сглаживание – простой и эффективный метод усреднения
по времени ФВР для оценки его основных статистик. Модель
экспоненциальной скользящей средней (exponential moving average - EMA )
имеет вид линейного разностного уравнения первого порядка
y n x n 1 y n 1 ; 0 1 - параметр сглаживания
x n - текущий отсчет ряда ; y n - модель тренда ; EMA - БИХ фильтр
K 1
y n 1 k x n k 1 K y 0 ; n K
y 0
k 0
- начальное значение EMA ;
y n
K
h MA k x n k ;
k 0
1 n , n 0
h MA n
,n 0
0
Импульсная характеристика EMA
2.
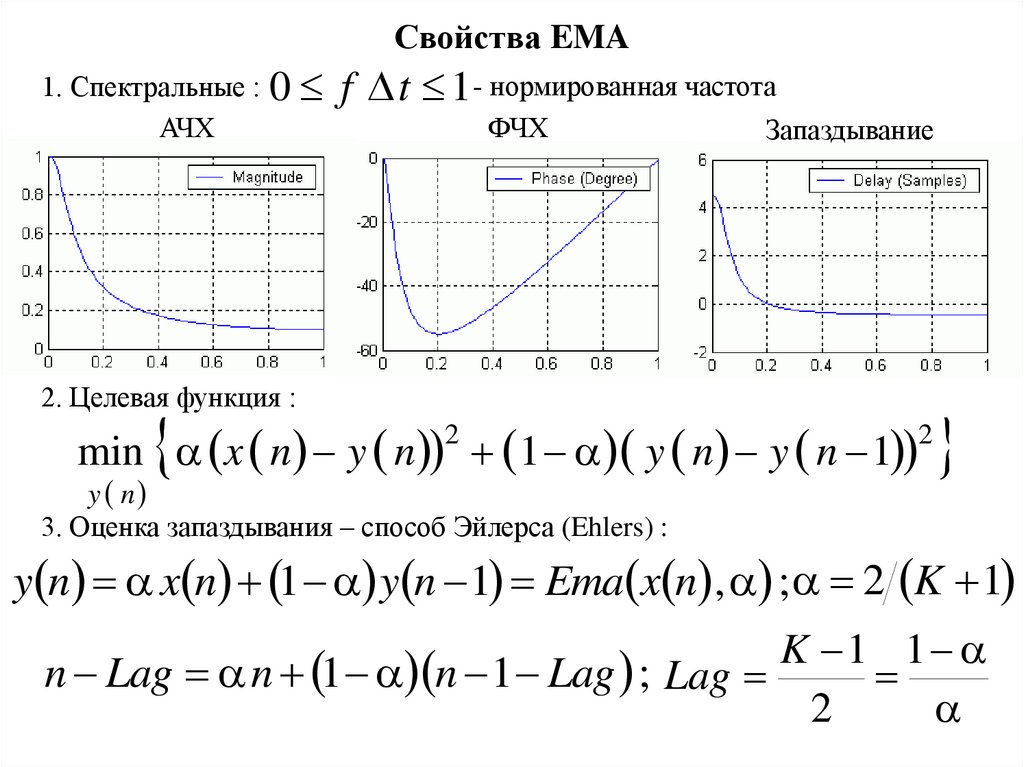
Свойства EMA1. Спектральные :
АЧХ
0 f t 1- нормированная частота
ФЧХ
Запаздывание
2. Целевая функция :
min x n y n 1 y n y n 1
2
y n
3. Оценка запаздывания – способ Эйлерса (Ehlers) :
2
y n x n 1 y n 1 Ema x n , ; 2 K 1
K 1 1
n Lag n 1 n 1 Lag ; Lag
2
3.
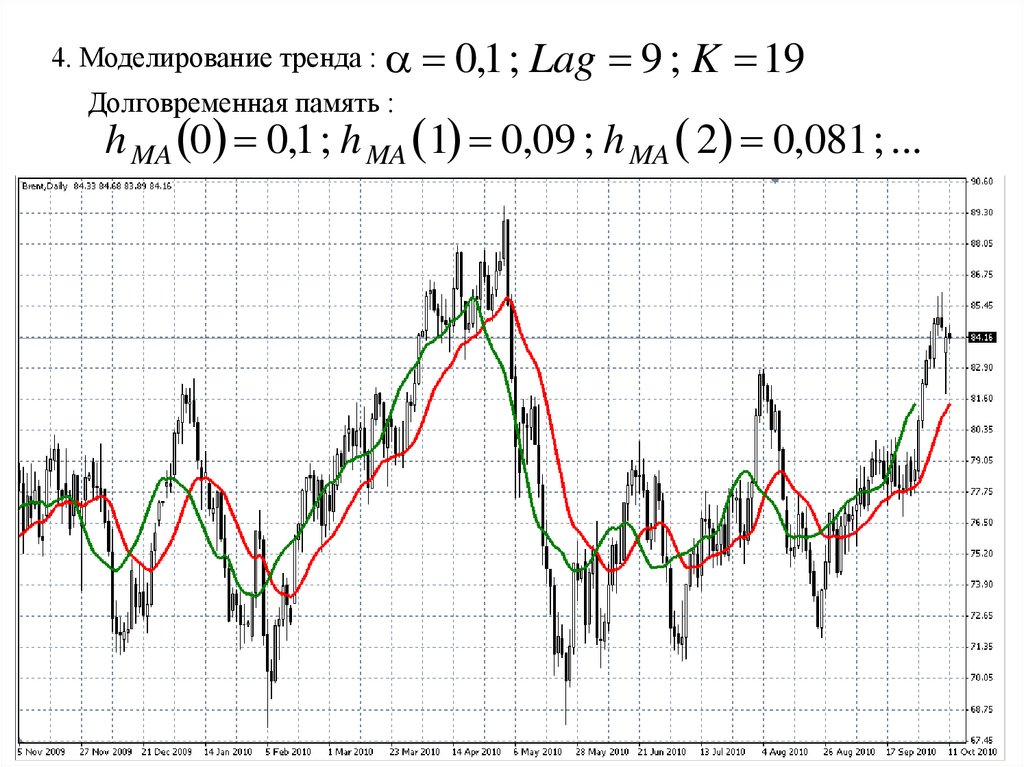
4. Моделирование тренда :Долговременная память :
0,1 ; Lag 9 ; K 19
h MA 0 0,1 ; h MA 1 0,09 ; h MA 2 0,081 ; ...
4.
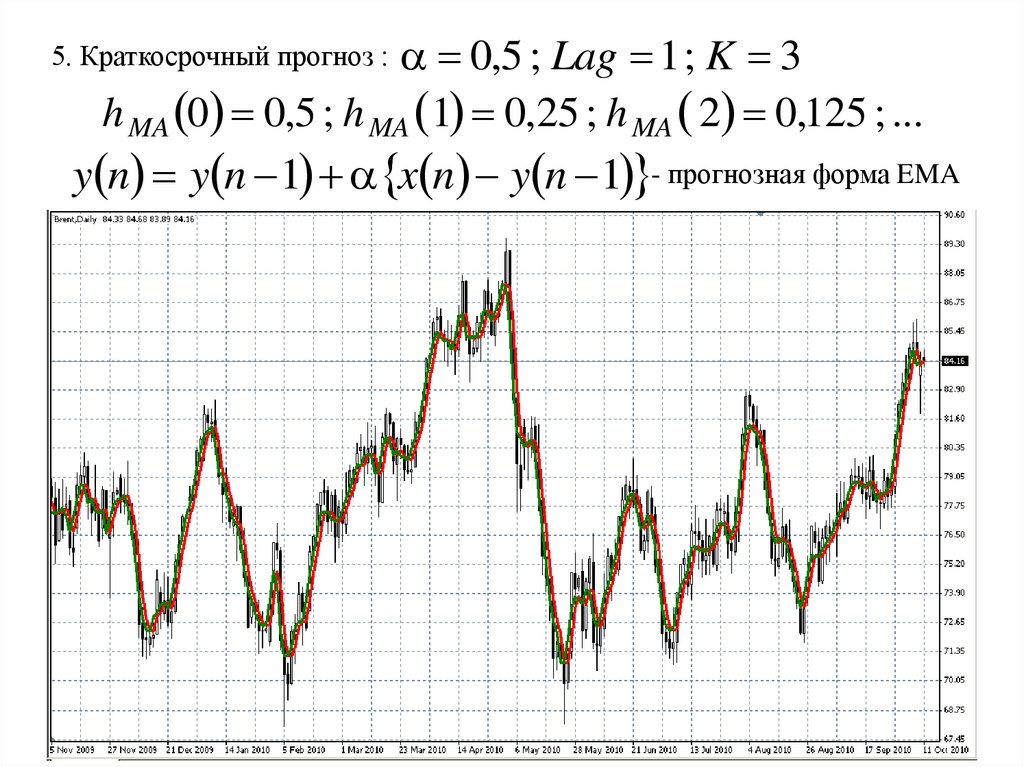
0,5 ; Lag 1 ; K 3h MA 0 0,5 ; h MA 1 0,25 ; h MA 2 0,125 ; ...
y n y n 1 x n y n 1 - прогнозная форма EMA
5. Краткосрочный прогноз :
5.
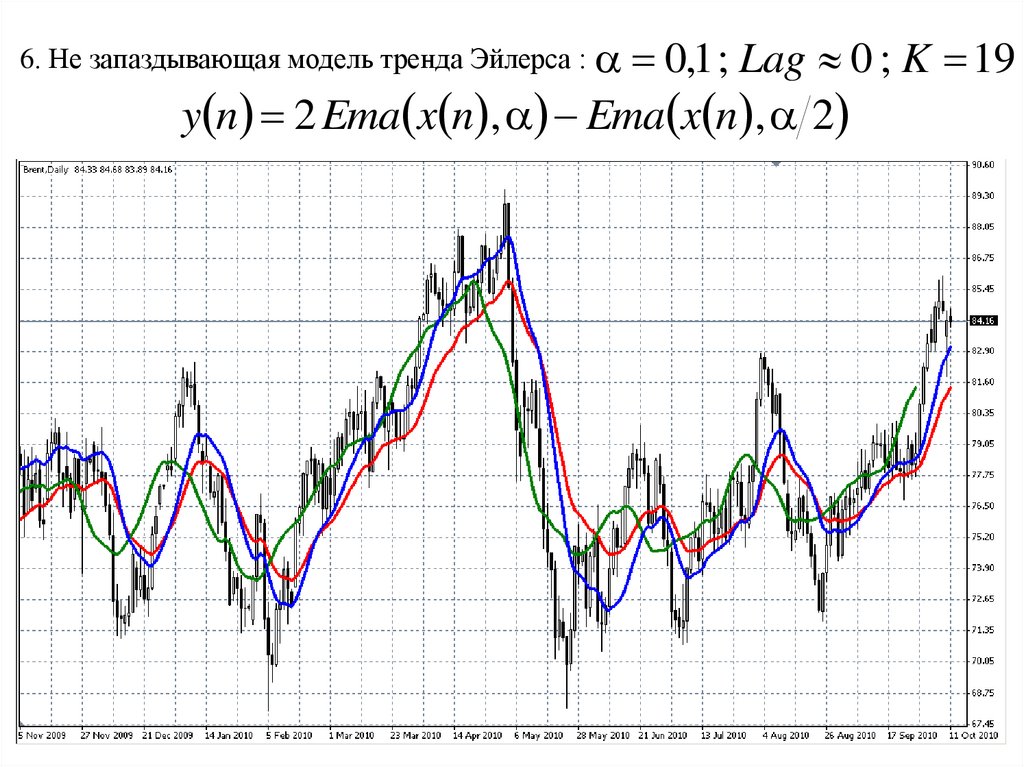
0,1 ; Lag 0 ; K 19y n 2 Ema x n , Ema x n , 2
6. Не запаздывающая модель тренда Эйлерса :
6.
Модифицированная EMA Булашова (MEMA)1. Целевая функция :
x n y n 2 y n y n 1 2
min
2
y n
y n 2 y n 1 y n 2
0 , 0 , 0 - параметры регуляризации; 1
y n x n 1 y n 1 y n 1 y n 2
2. Оценка запаздывания :
n Lag n 1 n 1 Lag
n 1 Lag n 2 Lag ;
Lag 1 ;
1 ; 1 Lag 1 0,5 - штраф за сложность ;
3. Управляемые параметры MEMA :
Lag 9 - запаздывание относительно ВР ; - степень гладкости тренда
1 Lag 1 0,5 Lag 1 - параметр сглаживания
7.
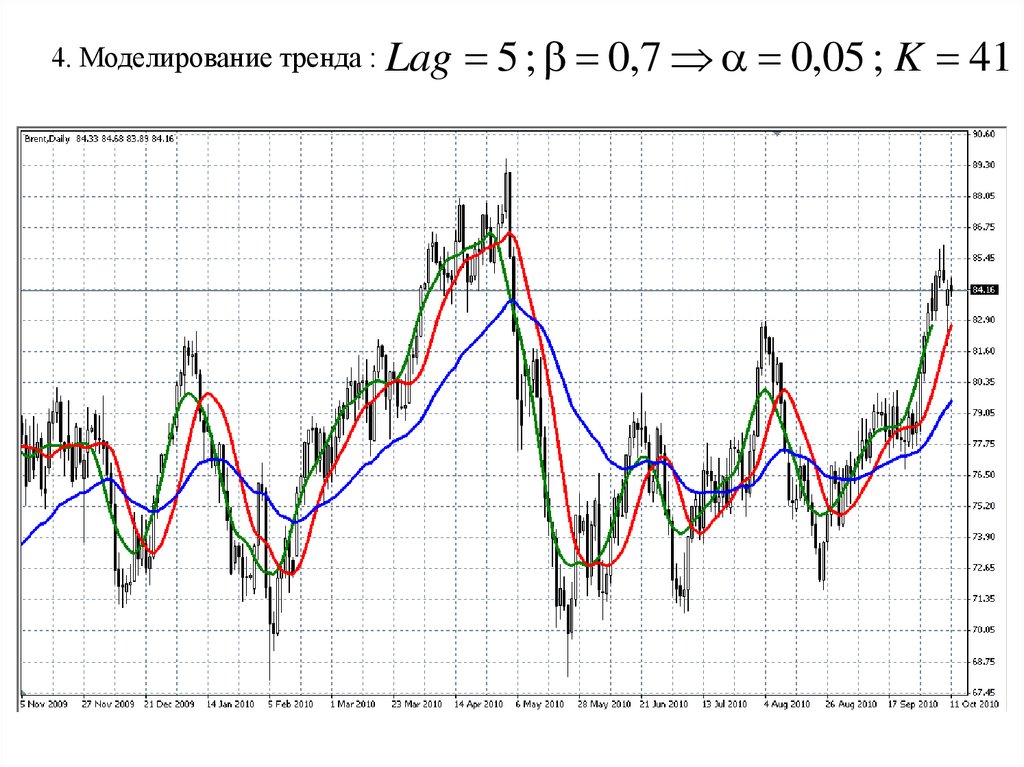
4. Моделирование тренда :Lag 5 ; 0,7 0,05 ; K 41
8.
4. Импульсная характеристика MEMA :1 2 2
1 1 1
y n
h MA k
h MA k x n k
2 1
k 0 2 1
MEMA – двухкомпонентная смесь Ema x n , 1 и Ema x n , 2
1, 2 1
1 2 4 2 ; 0 1 2 1
n
1 1, 2 , n 0
1, 2
h MA n
0
,n 0
9.
Модель линейного темпа изменения рынка Хольта - Брауна1. Прогноз рынка на один шаг времени (локально линейный тренд) :
~
x 1 n 1 ~
x n a 1 n 1 a 2 n 1
a 1 n 1 - среднее значение рынка в момент времени (n - 1) ;
a 2 n 1 - темп изменения рынка в момент времени (n - 1) ;
2. Алгоритм Хольта адаптации параметров локально линейного тренда :
a 1 n 1 x n 1 1 ~
x 1 n 1 ; 0 1 2 1
a 2 n 2 a 1 n a 1 n 1 1 2 a 2 n 1
3. Алгоритм Хольта в терминах ошибки прогноза рынка на один шаг времени :
e n x n ~
x 1 n 1
a 1 n a 1 n 1 a 2 n 1 1 e n
a 2 n a 2 n 1 1 2 e n
10.
11.
4. Алгоритм Брауна в терминах ошибки прогноза рынка на один шаг времени :0 1 - коэффициент дисконтирования, характеризует
старение данных за один шаг времени
2
2
1
1
1 1 ; 1 2
Шаг 0 : Инициализация. Выбрать параметр сглаживания
1 1
0 1
и начальные значения : n 1 ; ~
x 1 0 ; a 1 0 ; a 2 0
2
Шаг 1 : Вычислить ошибку прогноза рынка на один шаг времени :
e n x n ~
x 1 n 1
Шаг 2 : Корректировать среднее значение рынка за один шаг времени :
a 1 n a 1 n 1 a 2 n 1 e n
Шаг 3 : Корректировать темп изменения рынка за один шаг времени :
2
a 2 n a 2 n 1 1 1 e n
Шаг 4 : Вычислить прогноз рынка на один шаг времени :
~
x 1 n a 1 n a 2 n
Шаг 5 : Цикл по времени n = n + 1. Идти к Шагу 1.
12.
5. Адаптация параметра сглаживания по ошибке прогноза рынкаСледящий контрольный сигнал Брауна :
K 1
C B n e n k Ema e n , ; 0 1
k 0
Условие адекватности модели исходному ВР : C B n Cmax
Недостатки контрольного сигнала Брауна :
1. может не вернуться в допустимые пределы, даже если модель
будет вновь адекватна исходному ВР;
2. может превышать допустимые пределы, а модель формирует
достаточно точный прогноз.
Следящий контрольный сигнал Тригга :
CT n Ema e n , Ema e n , ; CT n 1
Условие адекватности модели исходному ВР :
P CT n Cmax 0,95 ; Cmax 2,4 2
Модель Брауна адаптации параметра сглаживания : n C n
T
13.
6. Функция распределения контрольного сигнала Тригга для однократногоэкспоненциального сглаживания :
7. Практическая модель адаптации параметра сглаживания :
min , min CT n
n CT n , min CT n max
max , max CT n
14.
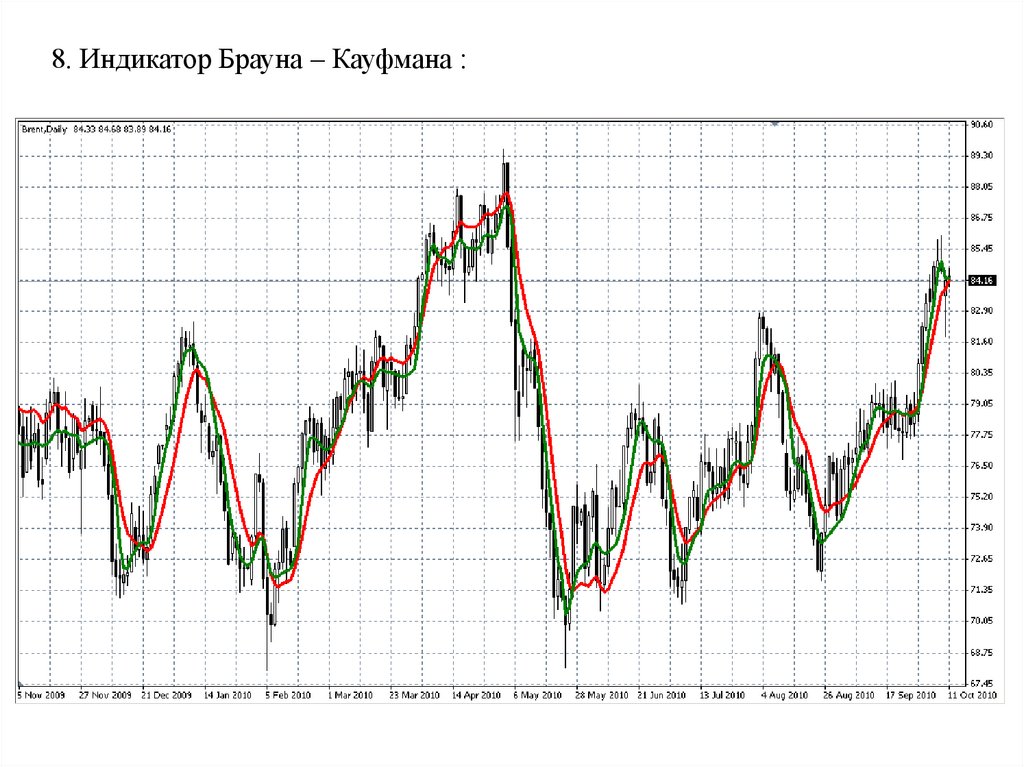
8. Индикатор Брауна – Кауфмана :15.
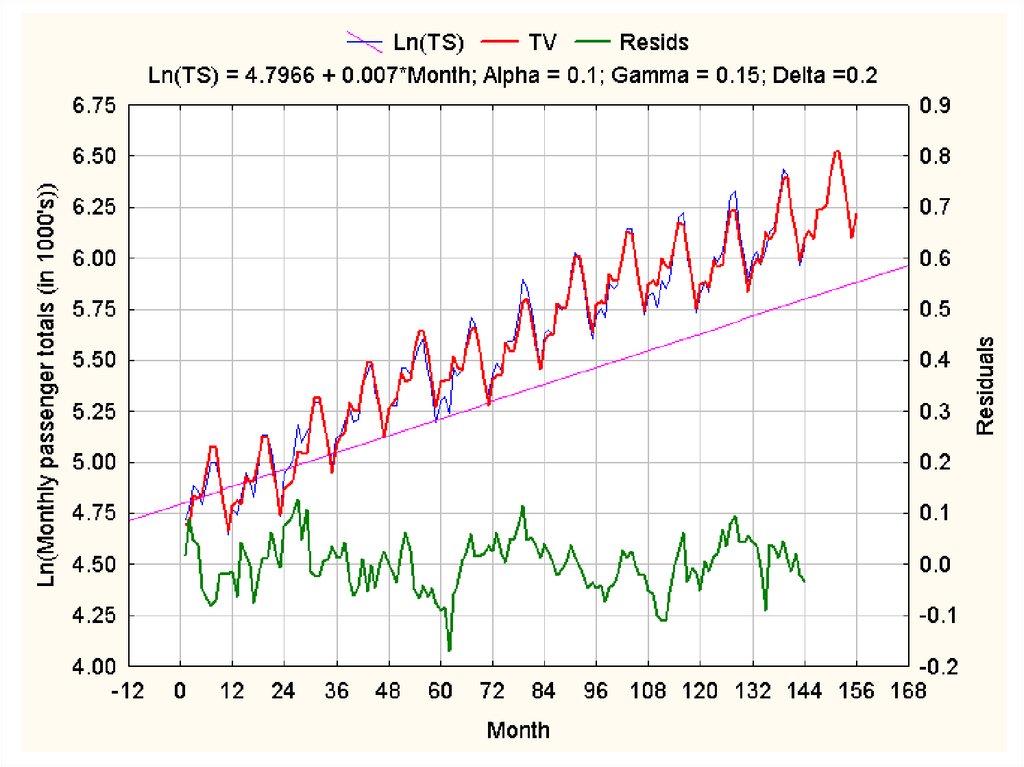
Сезонные модели экспоненциального сглаживанияАддитивный сезонный цикл Тейла – Вейджа
1. Прогноз рынка на один шаг времени :
~
x n a~ n c n T 1 ; a~ n a 1 n 1 a 2 n 1
a 1 n 1 - среднее значение рынка в момент времени (n - 1) ;
a 2 n 1 - темп изменения рынка в момент времени (n - 1) ;
c n T - значение рыночного цикла в момент времени (n – T ) ;
2. Алгоритм Тейла – Вейджа (ТВ) адаптации параметров сезонного цикла :
a 1 n 1 x n c n T 1 1 a~ n
a 2 n 2 a 1 n a 1 n 1 1 2 a 2 n 1
c n 3 x n a 1 n 1 3 c n T
0 1 2 3 1
16.
3. Алгоритм ТВ в терминах ошибки прогноза рынка на один шаг времени :Шаг 0 : Инициализация. Выбрать параметры сглаживания
1 , 2 , 3
и начальные значения :
n T ; ~
x T ; a 1 T 1 ; a 2 T 1 ; c k , k 0 ; (T 1)
Шаг 1 : Вычислить прогноз рынка на один шаг времени :
~
x n a 1 n 1 a 2 n 1 c n T
Шаг 2 : Вычислить ошибку прогноза рынка на один шаг времени :
e n x n ~
x n
Шаг 3 : Корректировать среднее значение рынка за один шаг времени :
a 1 n a 1 n 1 a 2 n 1 1e n
Шаг 4 : Корректировать темп изменения рынка за один шаг времени :
a 2 n a 2 n 1 1 2 e n
Шаг 5 : Корректировать сезонный цикл за один шаг времени :
c n c n T 3 1 1 e n
Шаг 6 : Цикл по времени n = n + 1. Идти к Шагу 1.
17.
18.
19.
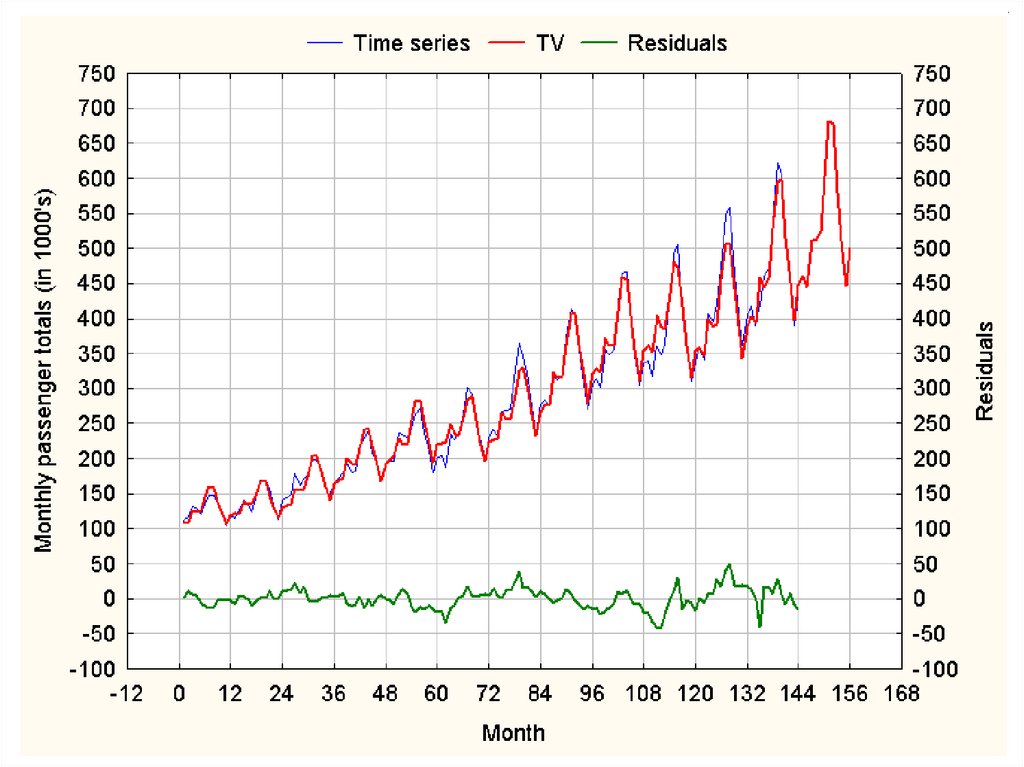
Мультипликативный сезонный цикл Винтерса1. Прогноз рынка на один шаг времени :
~
x n a~ n c n T 1 ; a~ n a 1 n 1 a 2 n 1
a 1 n 1 - среднее значение огибающей в момент времени (n - 1) ;
a 2 n 1 - темп изменения рынка в момент времени (n - 1) ;
c n T - значение рыночного цикла в момент времени (n – T ) ;
2. Алгоритм Винтерса адаптации параметров сезонного цикла :
a 1 n 1 x n c n T 1 1 a~ n
a 2 n 2 a 1 n a 1 n 1 1 2 a 2 n 1
c n 3 x n a1 n 1 3 c n T
0 1 2 3 1

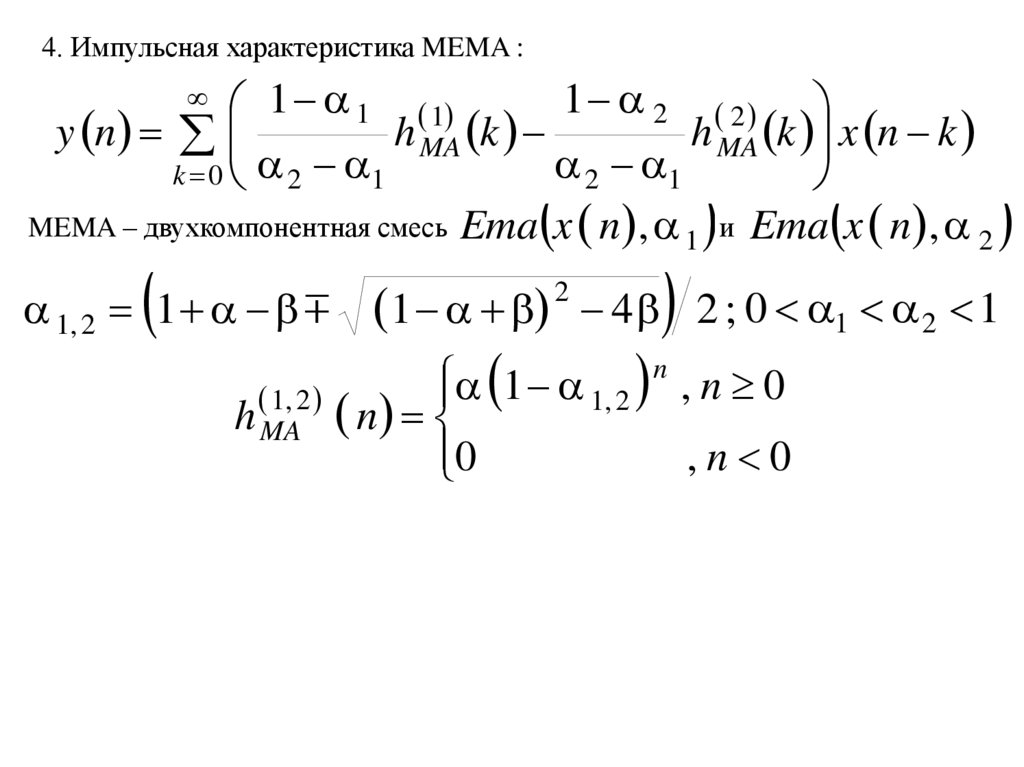








 Математика
Математика








