Похожие презентации:
Способы задания и свойства числовых последовательностей
1. Способы задания и свойства числовых последовательностей. Бесконечно убывающая геометрическая последовательность
2.
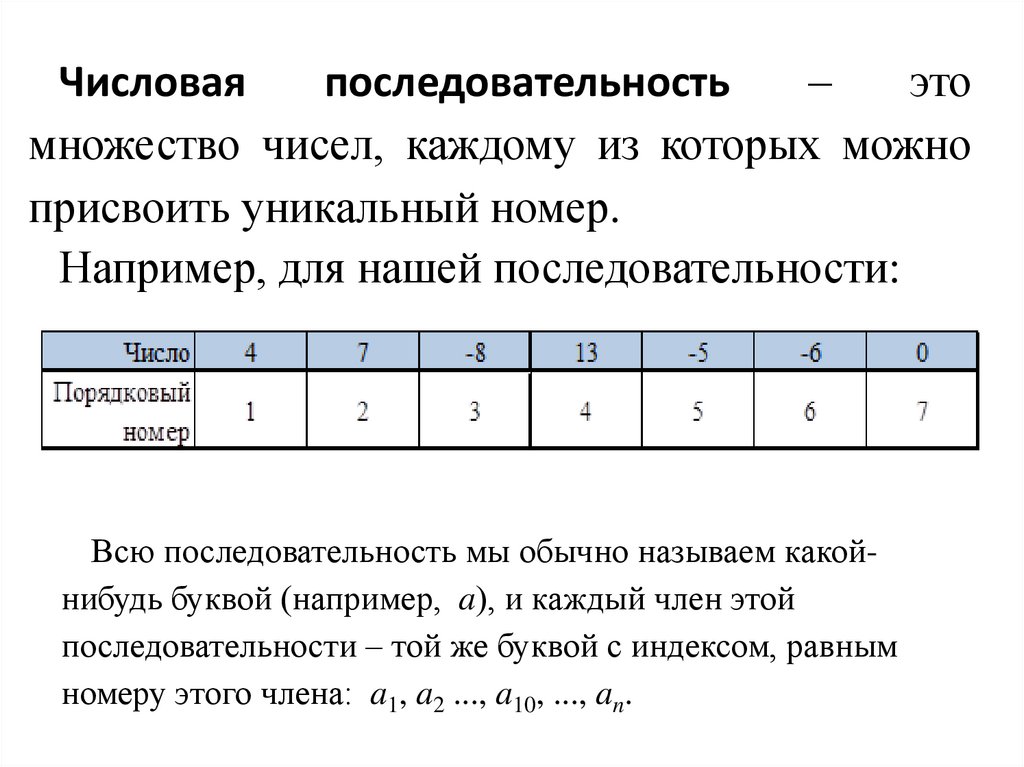
Числоваяпоследовательность
–
это
множество чисел, каждому из которых можно
присвоить уникальный номер.
Например, для нашей последовательности:
Всю последовательность мы обычно называем какойнибудь буквой (например, a), и каждый член этой
последовательности – той же буквой с индексом, равным
номеру этого члена: a1, a2 ..., a10, ..., an.
3.
ПоследовательностьОпределение 1.
Функцию вида у= f (х), х ϵ Ν называют
функцией натурального аргумента
или числовой последовательностью
и обозначают у = f (n) или
у1, у2,
у3,…, уn,…, или
(уn).
(аn) – последовательность
а1 ; а2 ; а3 ;…. аn - члены последовательности
Первый
член послед.
n-ый
член послед.
4. Свойства числовых последовательностей
Свойства числовых последовательностейПоследовательность {an} называется монотонной, если an+1≥ an
или an+1≤an для всех n.
В первом случае это монотонно неубывающая, во втором –
монотонно невозрастающая последовательность.
Если an+1>an или an+1< an для всех n, то говорят, что
последовательность {an} строго монотонна (возрастает в первом
случаем и убывает во втором).
Последовательность {an} называется ограниченной, если
существуют такие числа c и C, что для всех членов
последовательности выполняются неравенства c ≤ an ≤ C.
Ограниченной сверху называется последовательность, для которой
существует такое число C, что для всех членов последовательности
выполняется неравенство an ≤ C.
Ограниченной снизу называется последовательность, для которой
существует такое число c, что для всех членов последовательности
выполняется неравенство an ≥ С.
Если говорят, что последовательность ограничена, это означает, что она
ограничена и сверху и снизу.
5.
Если существует такое натуральное T, что, начиная с некоторого n,выполняется равенство an = an+1, то последовательность
называется периодической, а T-длиной её периода.
Используя понятия монотонности, ограниченности и периодичности,
можно описать немало простейших свойств последовательностей. Вот
некоторые из них:
1) Если последовательность {an} монотонно возрастающая, то
последовательность {-an} монотонно убывающая, и наоборот.
2) Если последовательность {an} монотонно невозрастающая, то
последовательность {-an} монотонно неубывающая, и наоборот.
Монотонно возрастающая ограниченна снизу, монотонно
убывающая – сверху.
Монотонно возрастающая или монотонно убывающая
последовательность не может быть периодической.
Периодическая последовательность всегда ограничена.
6. Примеры бесконечных числовых последовательностей
• 1, 2, 3, 4, 5, … - последовательностьнатуральных чисел.
• 2, 4, 6, 8, 10,… - последовательность чётных
чисел.
• 1, 3, 5, 7, 9,… - последовательность нечётных
чисел.
• 1, 4, 9, 16, 25,… - последовательность
квадратов натуральных чисел.
• 2, 3, 5, 7, 11… - последовательность простых
чисел.
7. Способы задания числовых последовательностей
•Словесный•Аналитический
•Рекуррентный
8. Словесный способ.
Правило задания описано словами, безуказания каких-либо формул или когда
закономерности между элементами
последовательности нет.
Пример 1. Последовательность простых чисел:
2,3,5,7,11,13,17,19,23,29,31,… .
Пример 2. Произвольный набор чисел:
1,4,12,25,26,33,39,… .
Пример 3. Последовательность четных чисел:
2,4,6,8,10,12,14,16,… .
9.
10.
Примеры последовательностей.Продолжите ряд: 1, 10, 3, 9, 5, 8, 7, 7,
9, 6…
Продолжите ряд 77, 49, 36, 18…
11.
Примеры последовательностей.Продолжите ряд: 1, 10, 3, 9, 5, 8, 7, 7,
9, 6…
Ответ: Ряд состоит из двух частей: числа на
нечетных местах: 1, 3, 5, 7, 9...; числа на четных
местах: 10, 9, 8, 7
Продолжите ряд 77, 49, 36, 18…
Ответ: Перемножаются две цифры, входящие
в предыдущее число
12. Аналитический способ задания числовых последовательностей
Последовательность задана аналитически, еслиуказана формула n-ого члена.
Например,
1) yn=n2 – аналитическое задание последовательности
1, 4, 9, 16, …
2) yn=С – постоянная (стационарная)
последовательность
2) yn=2n – аналитическое задание последовательности
2, 4, 8, 16, …
13. Рекуррентный способ задания числовых последовательностей
Рекуррентный способ задания последовательностисостоит в том, что указывают правило,
позволяющее вычислить n-ый член, если
известны ее предыдущие члены
1) арифметическая прогрессия задается
рекуррентными соотношениями a1=a, an+1=an + d
2) геометрическая прогрессия b1=b, bn+1=bn * q
14.
Числа Фибоначчи.1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 3
Элементы числовой последовательности, в
которой каждое последующее число равно
сумме двух предыдущих чисел.
Леонардо Фибоначчи - итальянский
математик.
(родился около 1170 — умер после 1228),
Последовательность Фибоначчи
рекуррентно задать легко, а
аналитически – трудно.
n
1 1 5 1 5
xn
5 2 2
n
15. Последовательность чисел Фибоначчи
Филлотаксис (листорасположение) —правило, по которому располагаются,
например, семечки в соцветии
подсолнуха.
Семечки упорядочены
в два ряда спиралей,
один из которых идет
по часовой стрелке,
другой против неё.
16. Арифметическая прогрессия
Числовую последовательность, каждый членкоторой, начиная со второго, равен сумме
предыдущего члена и одного и того же числа
d, называют арифметической прогрессией, а
число
d
–
разностью
арифметической
прогрессии.
an+1 = an + d , n є N
d = an+1 - an
Пример: 1, 3, 5, 7, 9, 11, … возрастающая
арифметическая прогрессия,
у которой
d = 2.
17.
Определениеарифметической прогрессии
Разность арифметической
прогрессии
Формула n-го
члена арифметической
прогрессии
Сумма n первых
членов арифметической
прогрессии
Характеристическое
свойство арифметической
прогрессии
an+1 = an + d
d = an+1 - an
an = a1+ d · (n - 1)
a1 an
Sn
n
2
18. Геометрическая прогрессия
Числовую последовательность, все члены которойотличны от нуля и каждый член которой, начиная
со второго, получается из предыдущего члена
умножением на одно и то же число q, называют
геометрической
прогрессией,
а
число
q
–
знаменателем геометрической прогрессии.
bn = bn - 1 · q
bn = b1 ·
qn - 1
q=
Пример: 54 , 18, 6, 2, … -убывающая
геометрическая прогрессия,
у которой q = 1/3.
bn
bn - 1
19. Развитие учения о прогрессиях
Прогрессия (от латинского progressio) «движение вперёд»Наблюдая луну от новолуния до полнолуния,
вавилоняне пришли к такому выводу: в первые
пять дней после новолуния рост освещения
лунного диска совершается по закону
геометрической прогрессии со знаменателем 2.
20.
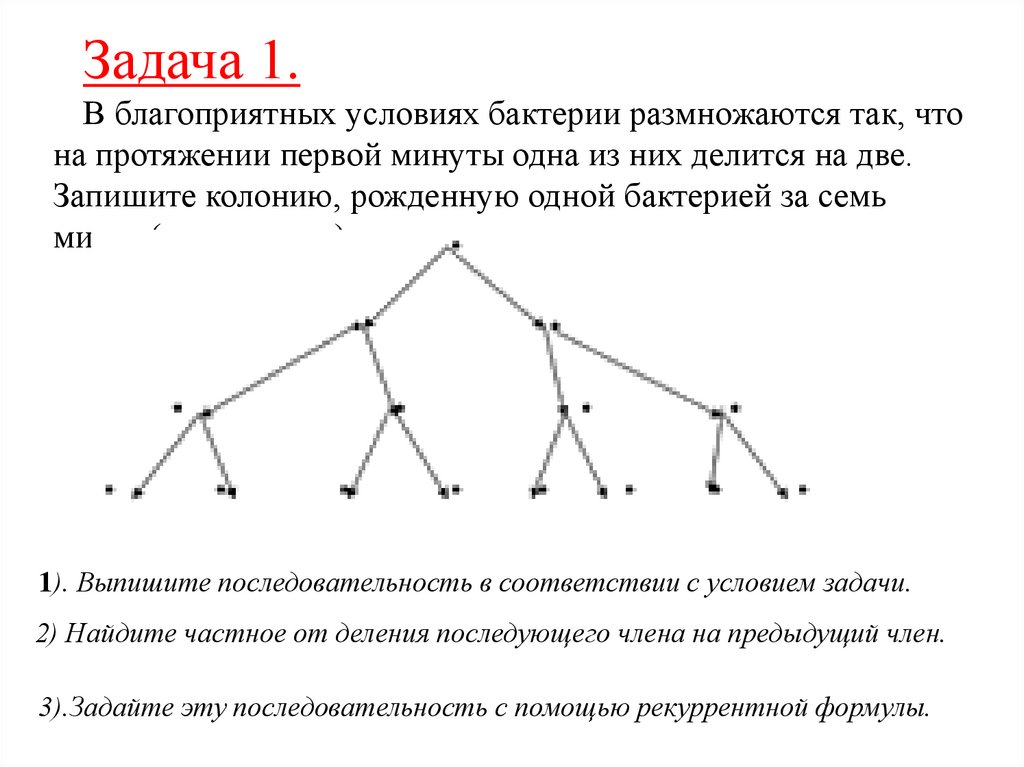
Задача 1.В благоприятных условиях бактерии размножаются так, что
на протяжении первой минуты одна из них делится на две.
Запишите колонию, рожденную одной бактерией за семь
минут.(см. рисунок).
1). Выпишите последовательность в соответствии с условием задачи.
2) Найдите частное от деления последующего члена на предыдущий член.
3).Задайте эту последовательность с помощью рекуррентной формулы.
21.
Решение:1). Выпишите последовательность в соответствии с условием задачи.
1;2;4;8;16;32;64.
или (bп) - последовательность,
b1 =1; b2=2;
b3=4; b4=8; b5=16; b6 =32;
b7 =64;
2) Найдите частное от деления последующего члена на предыдущий член.
b3 : b2 =4 : 2=2 ;
b4 : b3 =8 : 4=2;
b5 : b4 = 16 : 8=2; и т.д.
bп+1: b п = q q -знаменатель прогрессии.
q = b2:b1= b3:b2=b4:b3=…= bп+1: b п
3).Задайте эту последовательность с помощью рекуррентной формулы.
b2 = 2b1
b3= 2 b2
b4= 2b3…..
bп+1 = q b п
Такую последовательность в математике называют геометрической
прогрессией.
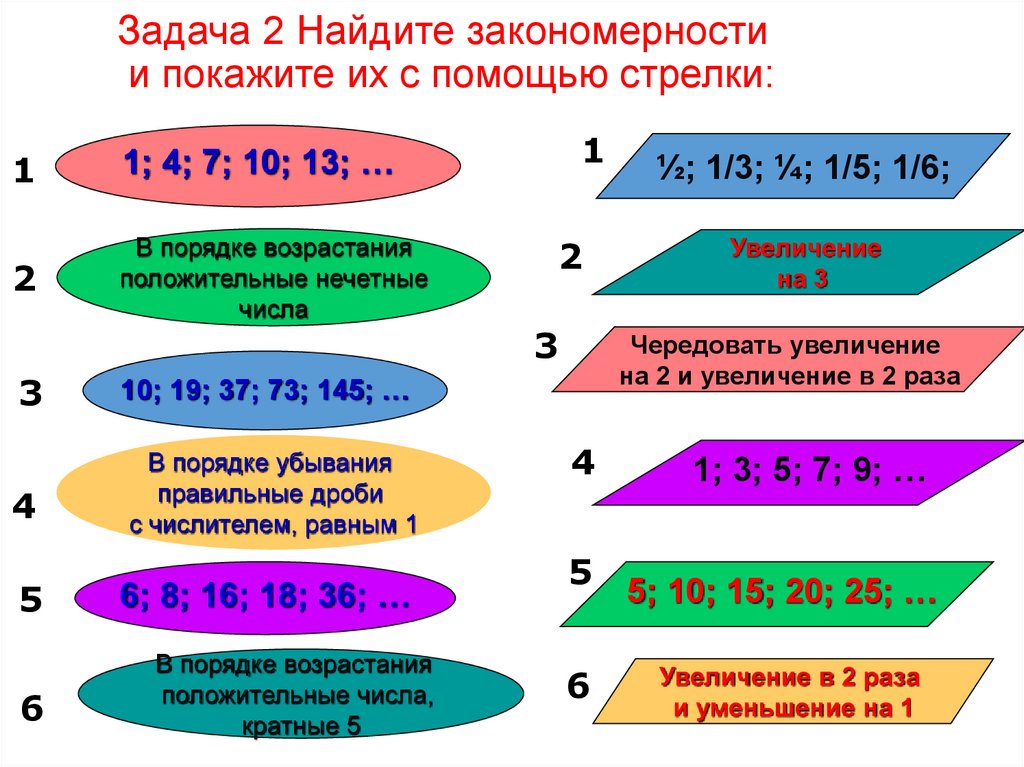
22. Задача 2 Найдите закономерности и покажите их с помощью стрелки:
11; 4; 7; 10; 13; …
2
В порядке возрастания
положительные нечетные
числа
1
2
3
3
4
5
6
6; 8; 16; 18; 36; …
В порядке возрастания
положительные числа,
кратные 5
Увеличение
на 3
Чередовать увеличение
на 2 и увеличение в 2 раза
10; 19; 37; 73; 145; …
В порядке убывания
правильные дроби
с числителем, равным 1
½; 1/3; ¼; 1/5; 1/6;
4
5
6
1; 3; 5; 7; 9; …
5; 10; 15; 20; 25; …
Увеличение в 2 раза
и уменьшение на 1
23. Найдите закономерности и покажите их с помощью стрелки:
1; 4; 7; 10; 13; …В порядке возрастания
положительные нечетные
числа
10; 19; 37; 73; 145; …
В порядке убывания
правильные дроби
с числителем, равным 1
6; 8; 16; 18; 36; …
В порядке возрастания
положительные числа,
кратные 5
½; 1/3; ¼; 1/5; 1/6;
Увеличение
на 3
Чередовать увеличение
на 2 и увеличение в 2 раза
1; 3; 5; 7; 9; …
5; 10; 15; 20; 25; …
Увеличение в 2 раза
и уменьшение на 1
24.
Задача 3Определить, какие числовые
последовательности являются
геометрической прогрессией, а
какие арифметической:
1. 3; 6; 12; 24; 48; 56…
2. 1; 12; 23; 34; 45 …
3. −99; 33; −11…
4. −6; 5; 17; 28; 39…
5. 64; 16; 4; 1…
6. 2; 4; 8; 18…
25.
Сравним наши ответы:Геометрическая прогрессия – 3, 6.
Арифметическая прогрессия – 2, 4.
Не является ни арифметической, ни
геометрической прогрессиями - 1, 5, 7.
26.
Геометрическая прогрессия {bn} - это числовая последовательность,первый член которой отличен от нуля, а каждый член, начиная со второго,
равен предыдущему, умноженному на одно и то же число q ≠ 0. Это число
называют знаменателем геометрической прогрессии.
q – это число, во сколько раз изменяется каждый последующий член
геометрической прогрессии.
Как вы думаете, каким может быть q?
Положительным и отрицательным, но не нулем. Допустим, что
положительное. Пусть в нашем случае
Чему равен второй член b2 и b3?
q у нас
q=3, а b1=4.
b2=4⋅3=12
b3=12⋅3=36
Соответственно, q>0, то все последующие члены прогрессии имеют одинаковый
знак – они положительны.
А что если q отрицательное? Например, q=−3, а b1=4. Чему равен второй
член b2 и b3?
b2=4⋅(−3)=−12
b3=−12⋅(−3)=36
Если q<0, то знаки членов геометрической прогрессии чередуются.
27.
q=−3, а b =4Вернемся к нашей последней прогрессии
и попробуем так же как и в
1
арифметической найти ее 6 член. Как вы уже догадываетесь, есть два способа его нахождения.
Последовательно умножаем каждый член на q.
b2=b1⋅ q =4⋅−3=−12
b3= b1⋅ q ⋅ q = b1⋅ q2 =−12⋅(−3)=36
b4= b1⋅ q ⋅ q⋅ q= b1⋅ q3 =36⋅(−3)=−108
b5= b1⋅ q4 =−108⋅(−3)=324
b6= b1⋅ q5 = 324⋅(−3)=−972
Вывод: Если нам нужно найти значение числа прогрессии с порядковым номером, то мы
умножаем первый член геометрической прогрессии b1 на знаменатель q в степени, которая
на 1 единицу меньше, чем порядковый номер искомого числа.
b4=4⋅(−3)4−1=4⋅(−3)3=−108
b6=b1⋅q 6−1
b6=4⋅(−3)6−1=4⋅(−3)5=−972
Приведем формулу в общий вид и получим:
bn=b1⋅qn−1
уравнение
членов
геометрической
прогрессии.
28.
Бесконечно убывающая геометрическая прогрессия.Совсем недавно мы говорили о том, что q может быть как
больше, так и меньше нуля, однако, есть особые
значения
q при которых геометрическая прогрессия
называется бесконечно убывающей. При −1<q<1 –
прогрессия называется бесконечно убывающей.
Для начала запишем какую-нибудь геометрическую
прогрессию, состоящую из 5 членов.
Допустим, b1=1, а q=1/2, тогда:
bn=b1⋅q n−1
b2=1⋅1/2=1/2
b3=1/2⋅1/2=1/4
b4=1/4⋅1/2=1/8
b5=1/8⋅1/2=1/16
Мы видим, что каждый последующий член меньше
предыдущего в 1/2 раза, но будет ли какое-либо число bn=0?
Вы сразу же ответите – «нет». Вот поэтому и бесконечно
убывающая – убывает, а нулем никогда не становится.
29.
Свойство арифметической прогрессии.an=(an+1+an−1)/2 - свойство членов арифметической
прогрессии.
Свойство геометрической прогрессии.
Как найти b3, зная b2 и b4?
Умножим
b2⋅b4=b1⋅q ⋅b1⋅q3= b12⋅q4
1) b2⋅b4=b12⋅q4
2) b3=b1⋅q2 следовательно b3=b2⋅b4 Почему?
((из 1) следует b12= b2⋅b4/ q4 , следовательно b1=b2⋅b4q4
подставим b1 в 2) и сократим q))
свойство членов геометрической прогрессии
30.
31.
Сумма членовгеометрической прогрессии.
32.
Формулы для прогрессийАрифметическая
Рекуррентная
формула
Формула п- члена
Формула суммы ппервых членов
Характеристическое
свойство
Если в прогрессии:
m+n=p+k, то
Связь между двумя
любыми членами
прогрессии и d или q
Формула суммы членов
бесконечно убывающей
прогрессии
Геометрическая
an 1 an d
bn 0, bn 1 bn q
an a1 d (n 1)
bn b1 q n 1
a1 an
Sn
n
2
an 1 an 1
an
2
b1 (1 q n )
Sn
1 q
am an a p ak
bm bn b p bk
a k am
d
k m
bn2 bn 1 bn 1
bk
q k m
bm
b1
Sn
1 q
33.
Задача 5Ученик 5 А класса Вася, заболел гриппом, но продолжает ходить в школу.
Каждый день Вася заражает двух человек, которые, в свою очередь, заражают
еще двух человек и так далее. Всего в классе 31 человек. Через сколько дней
гриппом будет болеть весь класс?
Итак, первый член геометрической прогрессии это Вася, то есть 1 человек. 2 -ой
член геометрической прогрессии, это те два человека, которых он заразил в
первый день своего прихода. Общая сумма членов прогрессии равна количеству
учащихся 5А. Соответственно, мы говорим о прогрессии, в которой:
Весь класс заболеет за 5 дней.































 Математика
Математика








