Похожие презентации:
Числовые последовательности
1. Закончился двадцатый век, Куда стремится человек? Изучен космос и моря, Строенье звезд и вся земля, Но математиков зовет
Известный лозунг«Прогрессио - движение
вперед»
2. Повторение :
Числовую последовательность,Дать определениекаждый
член которой, начиная со
второго, равен сумме предыдущего
арифметической прогрессии?
члена и одного и того же числа
d,называют арифметической
прогрессией.
Назовите формулу n-го члена
а
a
d
(
n
1
)
n
1
арифметической прогрессии.
3. В арифметической прогрессии известны Найдите
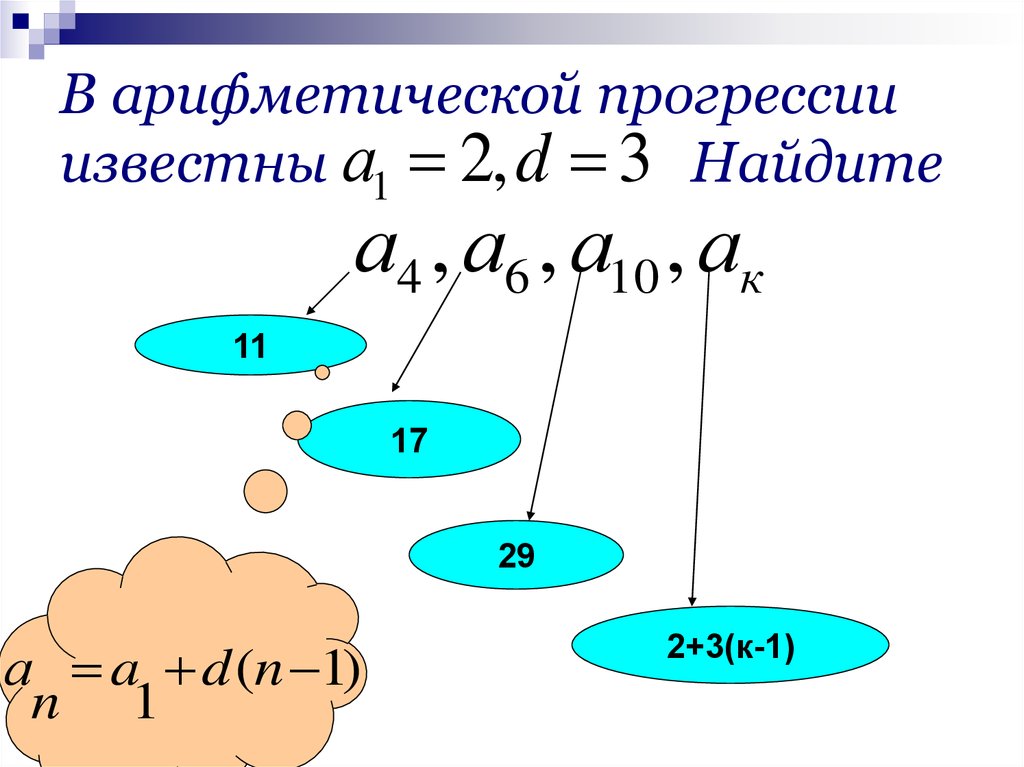
В арифметической прогрессииизвестны а1 2, d 3 Найдите
а4 , а6 , а10 , ак
11
17
29
а a d (n 1)
n 1
2+3(к-1)
4.
Числовые последовательностиСпособы
задания
аналитический
Словесный
рекуррентны
й
5. Каким способом задана последовательность Почему? Найдите её второй, четвертый, сотый члены?
Каким способом заданапоследовательность
аn 3n 1
5
Почему? Найдите её второй,
четвертый,
сотый
члены?
11
299
6. Последовательность задана формулой Как вы ее понимаете? Проговорите с помощью слов «предыдущий» и «последующий».
Последовательность заданас
формулой с
n
n 1
2
Как вы ее понимаете?
Проговорите с помощью слов
«предыдущий» и
«последующий».
7. Задача №1
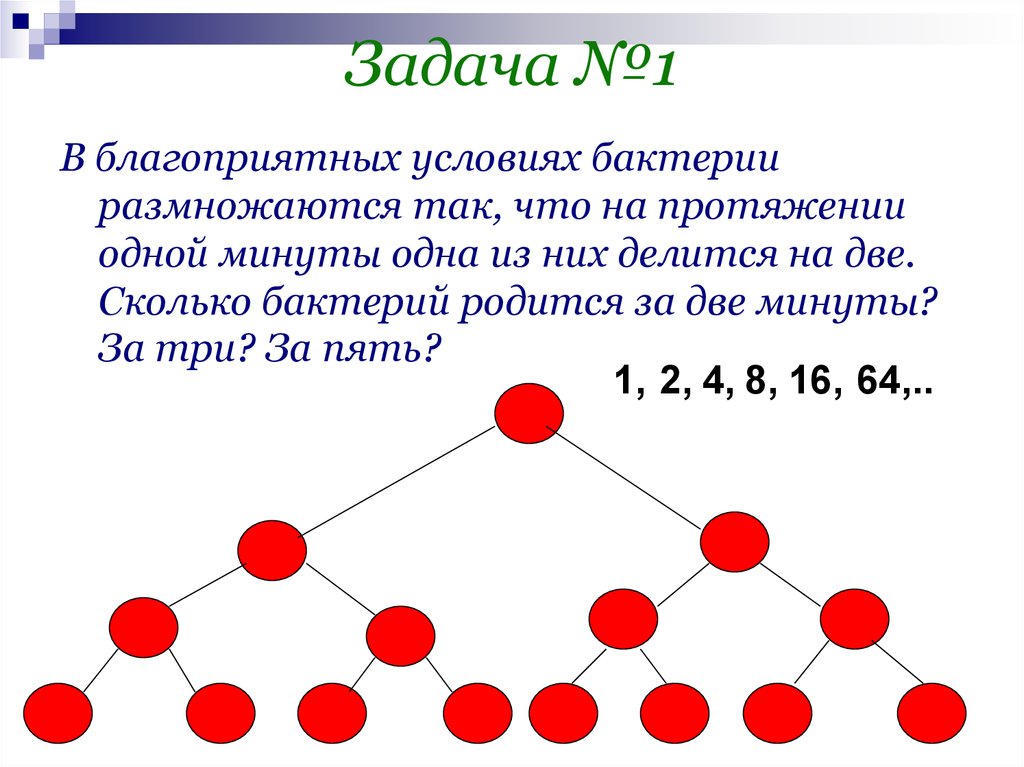
В благоприятных условиях бактерииразмножаются так, что на протяжении
одной минуты одна из них делится на две.
Сколько бактерий родится за две минуты?
За три? За пять?
1, 2, 4, 8, 16, 64,..
8. Задача №2
Имеется радиоактивное вещество, массой256г, вес которого за сутки уменьшается
вдвое. Какова станет масса вещества на
вторые сутки? На третьи? Восьмые?
256
?
6416, 8, 4, 2, 1,…
256, 128, 64, 32,
9. 1; 2; 4; 8; 16; 32; 64;….. 256; 128; 64; 32; 16; 8; 4; 2; 1;..
(умножение на 2)1; 2; 4; 8; 16; 32; 64;…..
(деление на 2
или
умножение
на 0,5)
256; 128; 64; 32; 16; 8; 4; 2; 1;..
10. «Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии»
«ПРОГРЕССИО – ДВИЖЕНИЕВПЕРЁД»
11. Цели урока:
Сформулировать определениегеометрической прогрессии.
Вывести формулу n-го члена
геометрической прогрессии
Рассмотреть применение изученной
теории на практике
12. определение
Числовую последовательность, всечлены которой отличны от нуля и
каждый член которой, начиная со
второго, получается из предыдущего
члена умножением его на одно и то же
число q называют геометрической
прогрессией.
q- называют знаменателем
геометрической прогрессии.
- геометрическая прогрессия
bn 0
(bn )
13. Будет ли геометрической прогрессией последовательность 2, 6, 18, 54,….
b3bn 1
b2
q
...
b1
b2
bn
q 0
Найдите знаменатель данной геометрической
прогрессии
а)1, 3, 9, 27, 81,….
б)512, 256, 128, 64,…
в)5, -5, 5, -5, 5,…
г)-2, 6, -18, 54,…
14. возрастающая геометрическая прогрессия убывающая геометрическая прогрессия
b1 0, q 1возрастающая
геометрическая прогрессия
b1 0,0 q 1
убывающая
геометрическая прогрессия
15. Вывод формулы n-го члена геометрической прогрессии
b1, qb2 b1 q
b3 b2 q b1 q q b1 q
2
b4 b3 q b1 q q b1 q
2
b5 b4 q b1 q q b1 q
3
3
4
...........................................
bn b1 q
n 1
16. формула n-го члена геометрической прогрессии
bn b1 qn 1
17. В данной геометрической прогрессии известны Найдите , ,
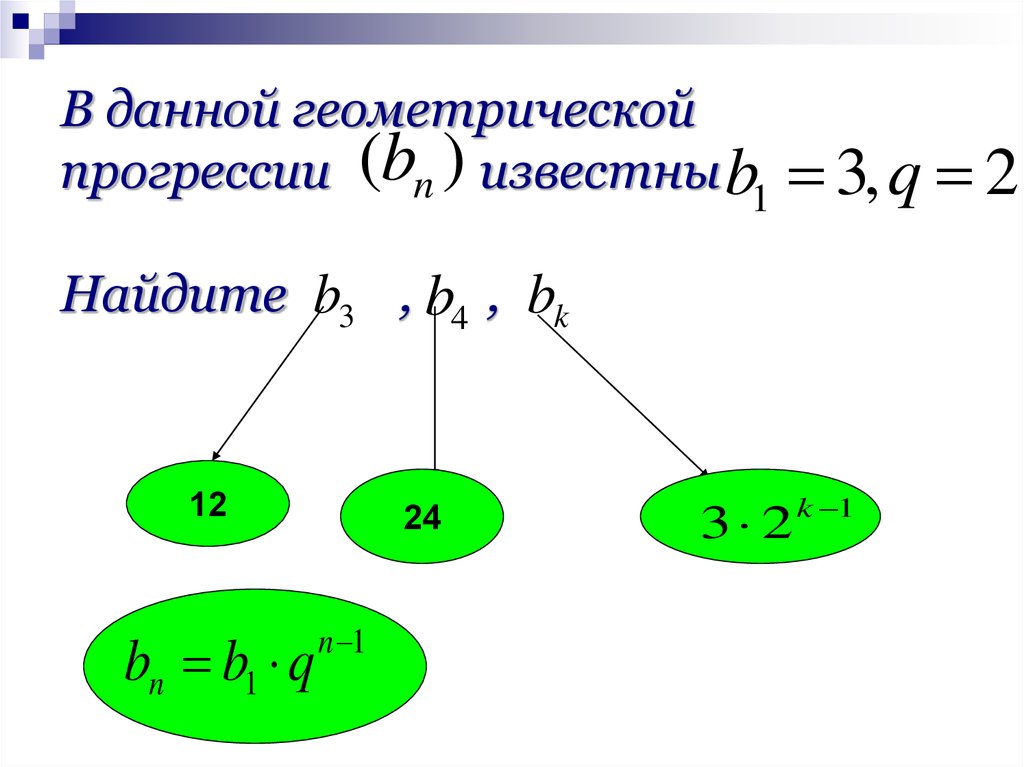
В данной геометрическойпрогрессии (bn ) известны b1
3, q 2
Найдите b3 , b4 , bk
12
bn b1 q
24
n 1
3 2
k 1
18. №476(а,б) Найдите первые шесть членов геометрической прогрессии
(bn )а) b1 1, q 3
b2 b1 q 3
1
б) b1 2, q
2
b2 1
b3 b2 q 9
b3
b4 27
b4
b5 81
b6 243
b5
b6
1
2
1
4
1
8
1
16
19. №476(а,б) Выразите указанные члены геометрической прогрессии через и
№476(а,б)Выразите указанные члены геометрической
прогрессии (bn ) через b и q
1
а)
b5 b1 q
б)
b41 b1 q
в)
г)
4
bк b1 q
40
к 1
b2 n b1 q
2 n 1
20. Является ли последовательность геометрической прогрессией? Если да, то найдите ее знаменатель. а) 3, 3, 3, 3, 3,…. б)2, 0, 0,
Является ли последовательность(bn )
геометрической прогрессией? Если да, то
найдите ее знаменатель.
а) 3, 3, 3, 3, 3,….
1
б)2, 0, 0, 0,…
в) 0, 4, 8, …
г) 3, 6, 12, 24, …
2
21. Составьте формулу n-го члена геометрической прогрессии
Составьте формулу n-го члена1 n 1
bn 64 ( )
геометрической прогрессии
2
а) 64, 32, 16,…..
б)
1 n 1
bn 2
1 1
4
, ,1,2,4,...
4 2
22.
bn b1 qn 1
23. Самостоятельная работа
Вариант А-1ВариантА-2
Найдите пятый член геометрической прогрессии
b1 3, q 2
Вариант В-1
b1 4, q 3
ВариантВ-2
Найдите седьмой член геометрической прогрессии , если
1
1
b5 , q
8
2
Вариант С-1
1
1
b3 , q
9
3
ВариантС-2
Найдите знаменатель геометрической прогрессии, если
4
х5 , х7 4
9
1
х4 2, х6
2
24. Домашнее задание
п.16, стр.131 учебникА: №476(в,г), №493(в,г)
В: №494(а,б),№484
С: №497(а,б),483


















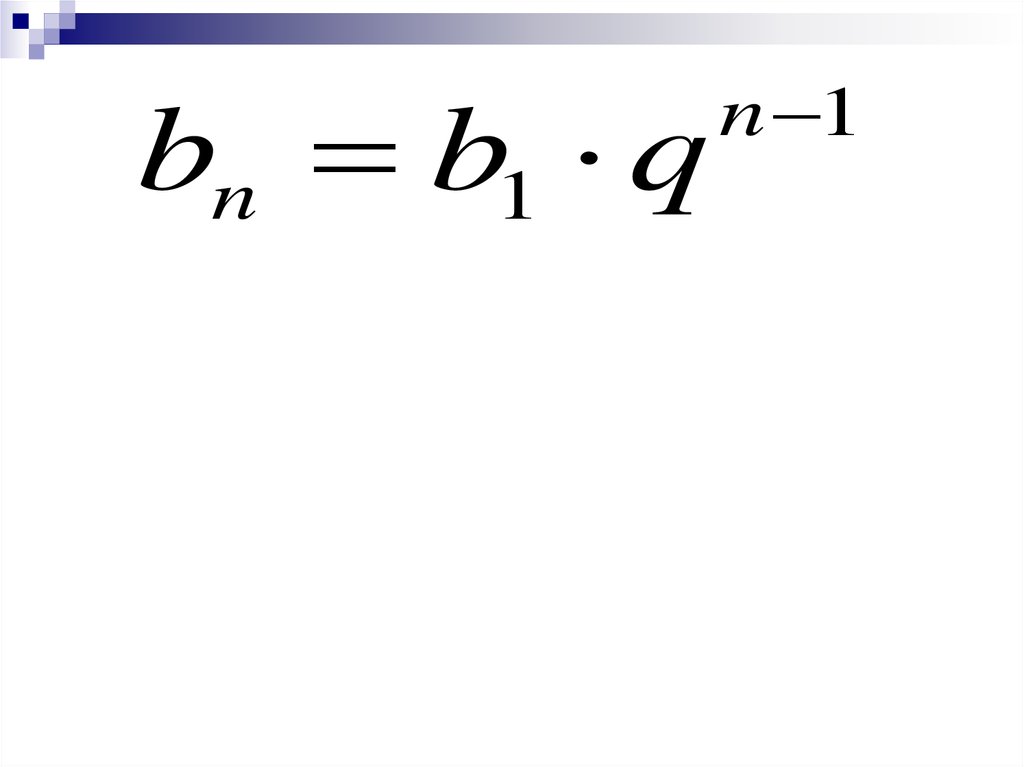



 Математика
Математика








