Логарифм. Логарифмическая функция. Логарифмические уравнения и неравенства

1.

МКОУ СОШ с.п.Кара-Суу Черекского района Кабардино-Балкарской Республики
Обобщающий урок по теме:
«Логарифм. Логарифмическая функция.
Логарифмические уравнения и неравенст ва.»
Учитель математики
Айшаева Фердаус Сулеймановна

2.

Цель урока:
- обобщение и систематизация знаний, навыков и умений по
теме.
Задачи:
- повторить определение логарифма, основное
логарифмическое тождество, простейшие свойства логарифмов,
определение и свойства логарифмической функции;
- закрепить способы решения логарифмических уравнений и
неравенств;
- развивать вычислительные навыки, навыки самостоятельной
работы, самоконтроля, навыки работы с различными
источниками информации, а также познавательный интерес к
предмету и логическое мышление;
- воспитывать информационную культуру учащихся,
аккуратность, дисциплинированность.
Оборудование: компьютер, мультимедийный проектор,
Интернет-ресурсы.

3.

Определение логарифма:
Логарифмом положительного числа b по
положительному и не равному единице основанию a
называется показатель степени, в которую нужно
возвести основание a, чтобы получить число b:
loga b=x, ax =b, где а > о, а ≠ 1,
b >0, x Є R,
Основное логарифмическое тождество
log
ab
a
b

4.

Свойства логарифмов:
1. Логарифм единицы по основанию а равен нулю:
loga1 = 0
2. Логарифм а по основанию а равен 1:
logaa =1
3. Cумма логарифмов равна логарифму произведения :
logaх + logaу = loga(xy), при x>0 и y>0
4. Разность логарифмов равна логарифму частного:
logaх - logaу = loga(x/y), x>0 и y>0

5.

5. Логарифм степени равен произведению показателя степени на
логарифм основания этой степени:
logaxp =plogax , х>0
для любого действительного числа р.
6.
1
log
x log
ax
an
n
для любых действительных m и n
7. Формула перехода от одного основания логарифма к другому основанию:
log
x
b
log
x
x
0
,
a
0
и
a
1
,
b
0
и
b
1
a
log
a
b
8.
2
n
log
x
2
n
log
x
,
(
n
Z
)
a
a

6.

Определение:
функция, заданная формулой у = logax,
где а > 0 и а 1,
называется логарифмической функцией.
у
a>1
4
У = logax
3
2
1
-2 -1
0
1
2
3
4
х
У = logax
0<a<1

7.

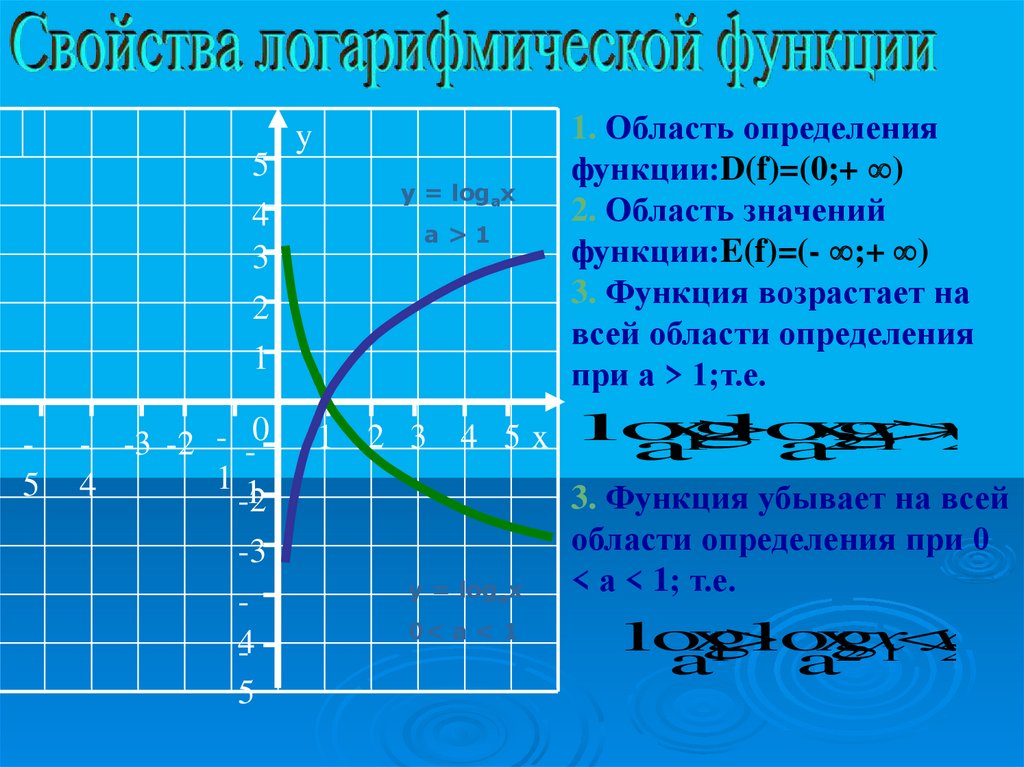
5
4
3
2
1
5
- -3 -2 - -0
11
4
-2
-3
45
y
y = logax
a>1
1. Область определения
функции:D(f)=(0;+ )
2. Область значений
функции:E(f)=(- ;+ )
3. Функция возрастает на
всей области определения
при а > 1;т.е.
x
log
x
,x
x
1 2 3 4 5 x log
1
a
a2 1 2
3. Функция убывает на всей
области определения при 0
< а < 1; т.е.
y = logax
0< a < 1
log
x
log
x
,x
x
1
2
1
2
a
a

8.

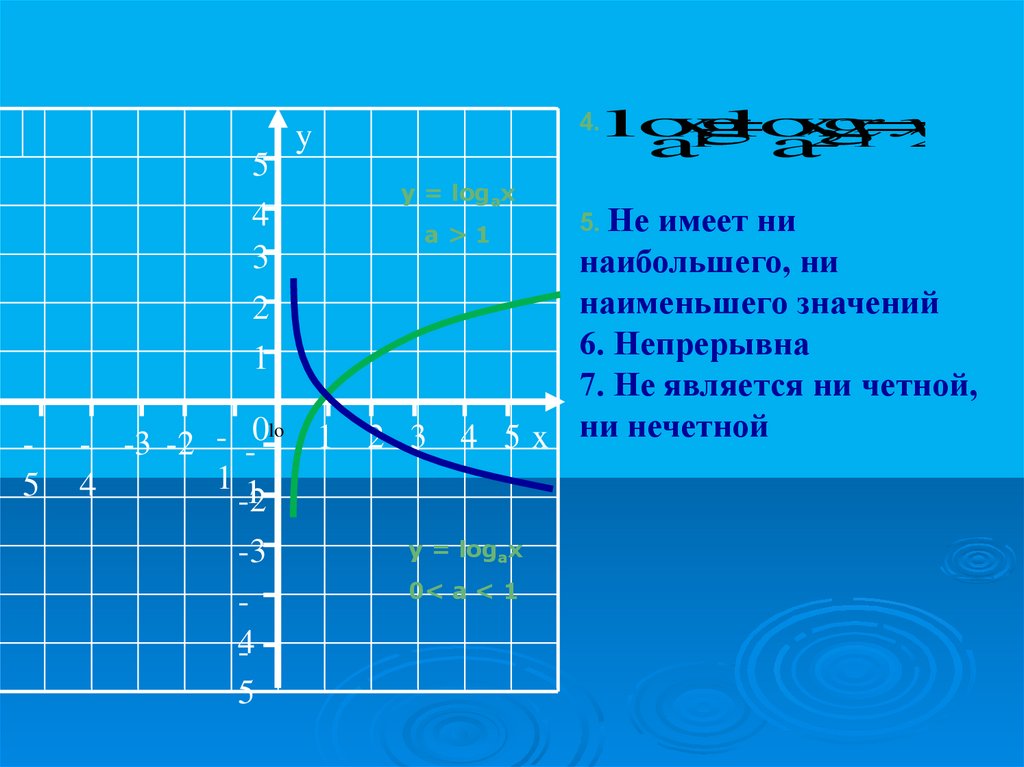
5
4
3
2
1
5
lo
- -3 -2 - -0
11
4
-2
-3
45
4. log
x
log
x
,x
x
a1 a2 1 2
y
y = logax
имеет ни
наибольшего, ни
наименьшего значений
6. Непрерывна
7. Не является ни четной,
1 2 3 4 5 x ни нечетной
a>1
y = logax
0< a < 1
5. Не

9.

Алгоритм решения логарифмических уравнений
1. Найти область допустимых значений (ОДЗ)
переменной;
2. Решить уравнение выбрав метод;
3. Проверить найденные корни непосредственной
подстановкой в исходное уравнение или
выяснить удовлетворяют ли эти корни условиям
ОДЗ.
f (x) F(x),
f (x) 0,
log
(
x
)
log
F
(
x
)
af
a
F(x) 0,
a 0, a 1.

10.

У кошки маленький котеночек подрос.
— Как дальше быть? — возник вопрос.
Решила мать, что в пору
Отдать котенка в школу.
И вот за партой в классе
Сидит пушистый Вася.
С усердием большим,
Как приказала мать,
Принялся кот науку постигать.
С терпеньем изучал,
По пунктам и по темам,
Строение мышей по графикам и схемам.
Решал он, чуть не плача,
И про бассейн задачу.
Сколь вытечет сметаны,
Когда открыть все краны.
И через 10 лет, науками богат,
Понес наш кот домой
Из школы аттестат.
И у какой-то горки
Мышонок вылезал из норки.
Но как его схватить?
Нельзя же прыгнуть сразу —
Тут надо применить
Научных знаний базу.
V — скорость, ускоренье — а,
И брызги сыплются с пера.
Затем привел он, глядя в книгу,
К логарифмическому виду.
Потом в системе «це, ге, ес»
Нашел его удельный вес.
Вписал последнюю строку
И приготовился к прыжку.
Пока ученый кот
Над уравненьем бился,
Мышонок — неуч
В норке скрылся.
Запомните, друзья, соль истины такой:
Теория мертва без практики живой.

11.

Рассмотрим несколько заданий на применение логарифмов из
открытого банка задач ЕГЭ 2013г.
В задания B3 ЕГЭ включены простейшие
логарифмические уравнения
АДРЕС САЙТА
http://www.mathege.ru:8080/or/ege/Main

12.

ЗАДАНИЯ B7 включают в себя
показательно-логарифмические
выражения.
http://www.mathege.ru:8080/or/ege/Main

13.

Решить уравнение log3(2-x)-log3(2+x)-log3 x+1=0
ОДЗ:
x
0
x
0
2
x
0
x
2
0
x
2
2
x
0
x
2
Преобразуем уравнение, используя свойства логарифмов:
log3(2-x)+1=log3(2+x)+log3 x
log3(2-x)+log33 =log3(2+x)+logx
log3(2-x)3 =log3(2+x)x
6-3x=2x+x2
X2+5x-6=0
X1=-6; x2=1
x1=-6 не входит в ОДЗ и является посторонним корнем.
Ответ:1

14. 3) Решить уравнение

log
(
2
x
1
)
log
x
2
log
(
2
x
1
)
4
4
4
ОДЗ:
2x 1 0
1
1
x
x
2
x 0
2
x 0
Преобразуем данное уравнение
log
x 1
) log
2log
x 1
) 0
4(2
4x
4(2
log
x 1
) (log
2) 0
4(2
4x
log
x 1
) 0 2x 1 4
3
4(2
x
2 0 2
2 0
log
(log
4x
4x
x 16
Так как корнями уравнения являются значения x принадлежащие
интервалу (1/2;+∞), то и 3/2, и 16 принадлежат ОДЗ.
Ответ: 3/2,16

15. Решим систему уравнений

x
x
log
log
2
2
log
x
log
y
1
x
2
y
2
2
2
2y
y
2
2
4
y
2
y
12
0
4
y
x
12
0 2
2
4
y
x
12
0
4
y
x
12
0
2
4
y
2
y
12
0
D
4
192
196
2
143
y
1
8
2
2
14
y
2
2
8
Так как выражение содержащееся под знаком логарифма должно быть всегда
больше нуля, следовательно, x>0, y>0, значит y2=-2 не является корнем данной
системы. Подставим во второе уравнение значение y1=3/2 и решим его.
3
4( )2 x 12 0
2
9 x 12 0
x 3
Ответ: 3/2; 3

16.

Решить неравенство
log1/2(x2+2x-8)≥-4
Так как логарифмическая функция с основанием меньшим единицы
убывающей, то для всех
logа f(x)>logаg(x)
является
f(x)< g(x),
0<a<1,
f(x)>0,
g(x)>0
x<-4, x>2
Неравенство можно записать в следующем виде:
log1/2(x2+2x-8)≥log1/216
Так как логарифмическая функция с основанием ½ является убывающей, то для всех x из
области определения неравенства получаем (x2+2x-8)≤16
Таким образом, исходное неравенство равносильно системе неравенств
2
2
x
2
x
8
0
x
2
x
8
0
(
x
4
)(
x
2
)
0
x
[
6
;
4
)
(
2
;
4
]
2
2
(
x
4
)(
x
6
)
0
x
2
x
8
16
x
2
x
24
0
Ответ:
x
[
6
;4
)
(2
;4
]

17.

Решить уравнение типа С3 ЕГЭ
8
2
(x + 4 )log 4 (x +1 ) + ( 4 x)log 2 (x 1 ) log(x 1 ) = 0
3

18.

8
log( x 1 )( x 1 ) 0
3
x 4
8
8
log 2 ( x 1 ) ( 4 x ) log 2 ( x 1 ) log 2 ( x 1 ) log 2 ( x 1 ) 0
2
3
3
x 4
8
8
(
log 2 ( x 1 ) log 2 ( x 1 )) ( log 2 ( x 1 ) ( 4 x ) log 2 ( x 1 )) 0
2
3
3
x 4 8
8
(
) log 2 ( x 1 ) ( ( 4 x )) log 2 ( x 1 ) 0
2
3
3
3x 4
3x 4 2
log 2 ( x 1 )
* log 2 ( x 1 ) 0
6
3
2
3x 4
(log 2 ( x 1 ) log 2 ( x 1 ) 2 ) 0
6
3x 4
( x 1)
log 2
0
6
( x 1) 2
( x 4 ) log 4 ( x 1 ) ( 4 x ) log 2 ( x 1 )
ОДЗ:
x +1 > 0
x 1> 0 x >1
3x 4
2
0
x 1> 0
4
x
1
3
6
( x 1)
x 1
log 2
0
1
2
2
( x 1)
( x 1 )
x 1 ( x 1) 2
x 1 x2 2x 1
x2 3x 0
x ( x 3) 0
x2 0
x3 3
4
ОДЗ ; x 2 0 ОДЗ ; x 3 3 ОДЗ
3
4
Ответ : ; 3
3
x1

19.

Задание типа С4
В треугольнике АВС АВ=12, ВС = 6, СА = 10. Точка D лежит на прямой ВС
так, что BD:DC = 2:7. Окружности, вписанные в каждый из треугольников
ADC и ADB, касаются стороны AD в точках E и F. Найдите длину отрезка
EF.
Докажем сначала утверждение, что если окружность, вписанная в треугольник
АВС, касается его стороны СВ в точке F, то СF = 1 (АС CB AB)
2
Доказательство. Пусть Q и Е –точки касания вписанной
окружности треугольника АВС со сторонами АC и AB.
Тогда QC=СF, FB=BE, AE=AQ
А
y
Найдем полупериметр треугольника:
y
2x 2 y 2z
p
x y z
2
x p ( y z)
E
z
Q
x
С
F
x
z
В
Выразим x через стороны треугольника,
тогда
а в с
а в с
x
с
2
2

20.

Из истории.

21.

Теорию логарифмов
развил Дж. Непер.
Он разработал способы
вычисления
арифметических
выражений с помощью
логарифмов и составил
подробные таблицы
логарифмов.
(1550—1617)

22.

Вот вы когда-нибудь слыхали
О логарифмической спирали?

23.

Закручены по ней рога козлов
И не найдете вы на них нигде узлов.

24.

Моллюсков многих и улиток Ракушки тоже
все завиты.

25.

И эту спираль мы повсюду встречаем:
К примеру, ножи в механизме вращаем,
В изгибе трубы мы ее обнаружим,
Турбины тогда максимально послужат!

26.

В подсолнухе семечки тоже закручены
И паука все плетенья заучены.
Наверняка, и о том вы не знали,
Галактики тоже кружат по спирали!