Похожие презентации:
Решение неравенств методом интервалов. 9 класс
1. Урок алгебры в 9 классе
Решение неравенствметодом интервалов
Рагозина Н.А.
Учитель математики
ГБОУ СОШ № 520
2. Устная работа
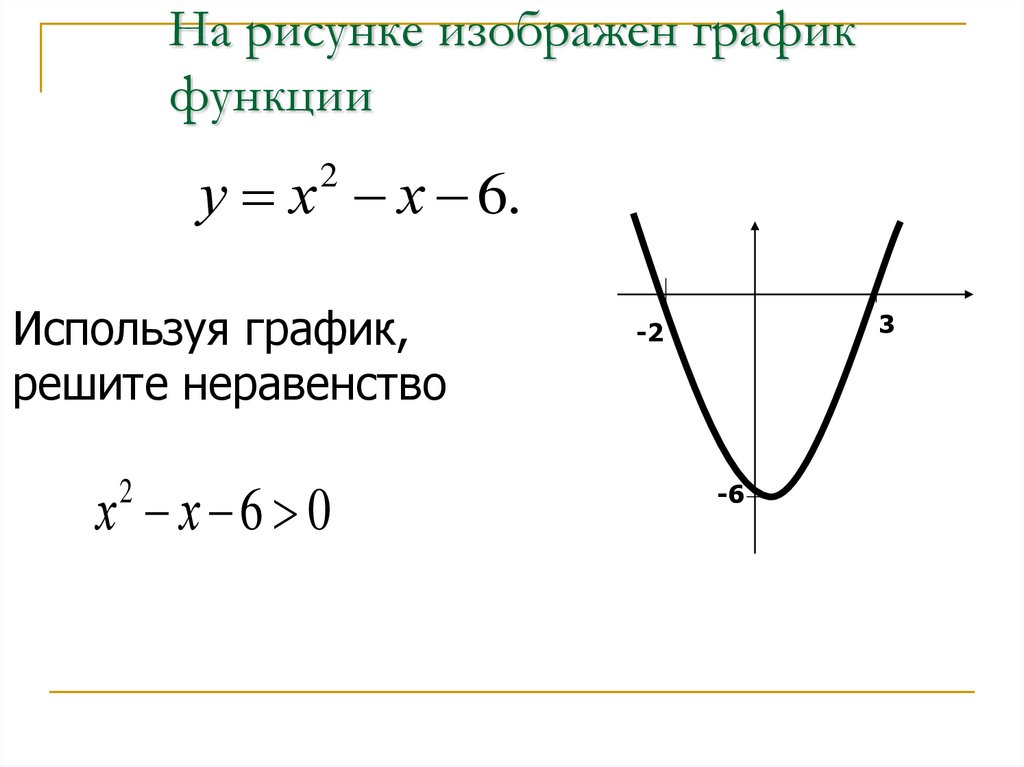
3. На рисунке изображен график функции
у х х 6.2
Используя график,
решите неравенство
х х 6 0
2
3
-2
-6
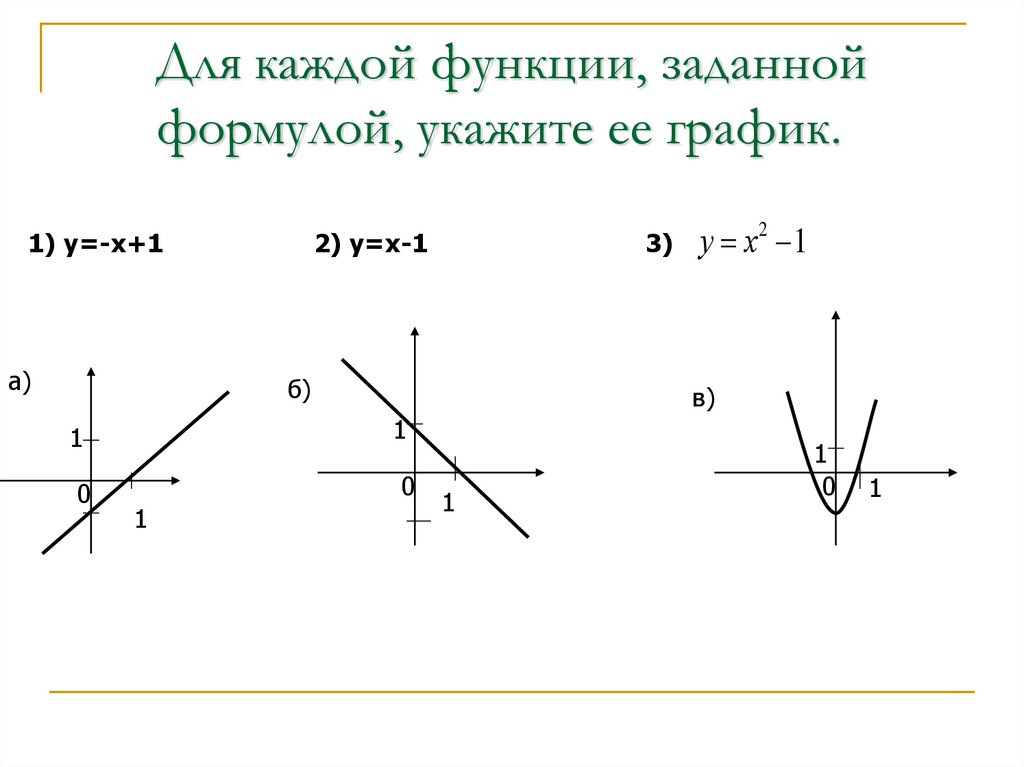
4. Для каждой функции, заданной формулой, укажите ее график.
1) у=-х+1а)
2) у=х-1
3)
б)
0
в)
1
1
0
1
у х2 1
1
1
0
1
5.
Ответьте на вопросыу
-2
0
2
х
-2
1. Определить область определения, область значений,
промежутки, когда функция принимает положительные
значения, промежутки, когда функция принимает
отрицательные значения, минимальное значение функции,
нули функции.
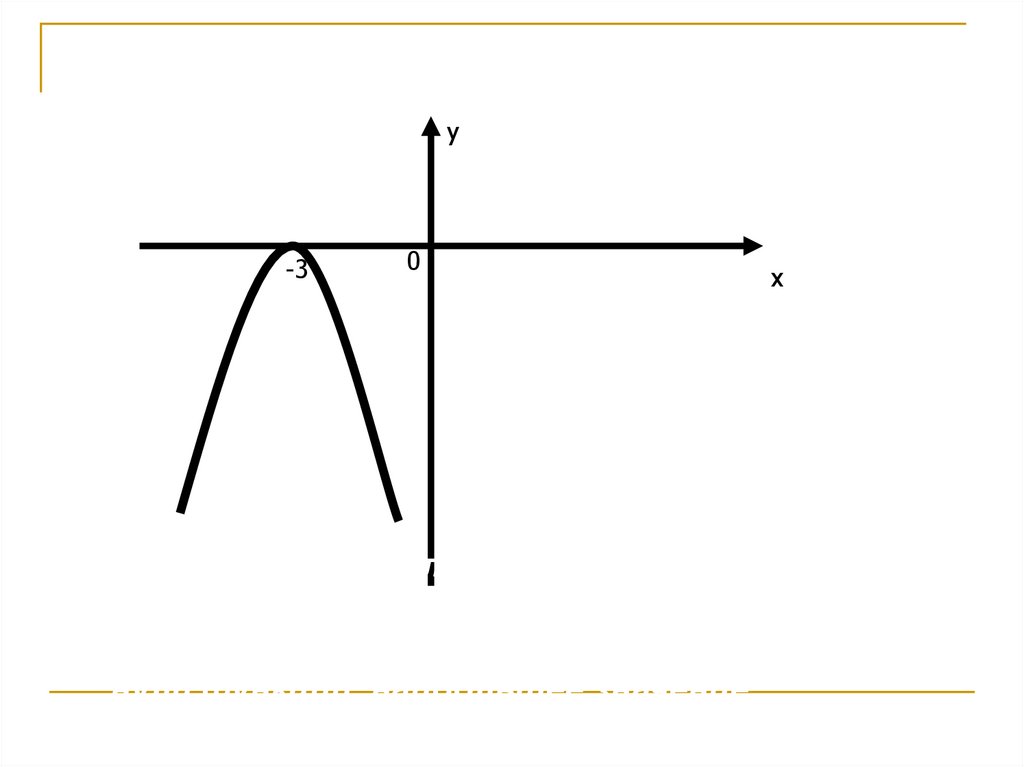
6.
у-3
0
х
2. Определить область определения,
область значений, неотрицательные
значения,
нули функции, наибольшее значение
функции.
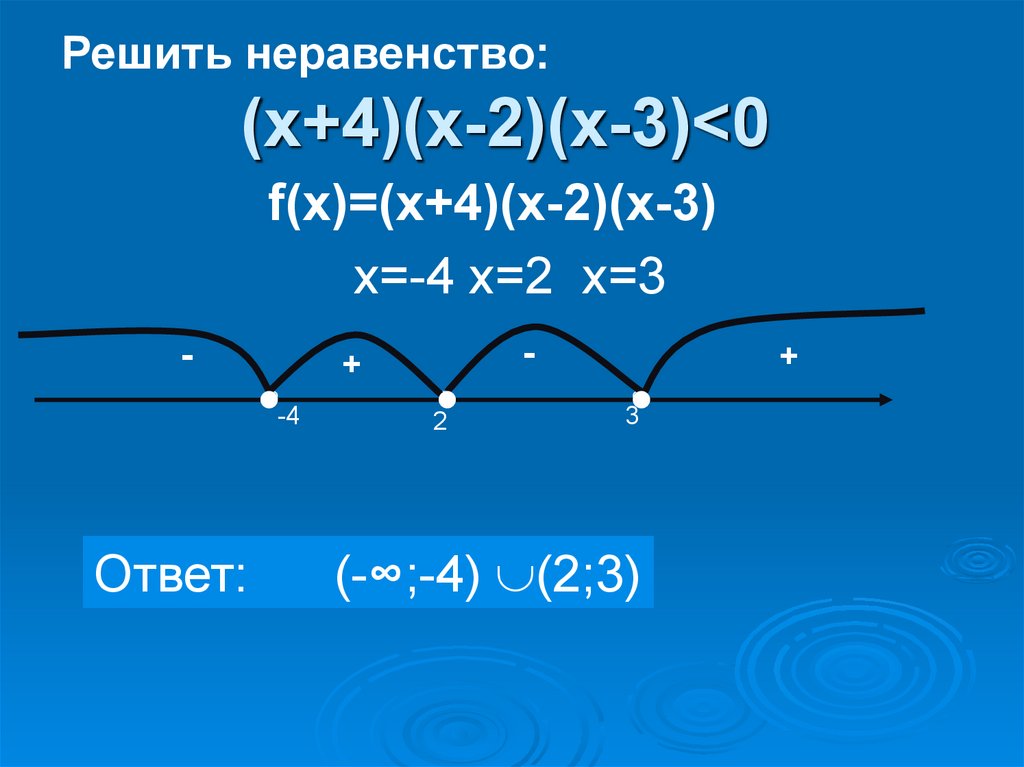
7. (х+4)(х-2)(х-3)<0
Решить неравенство:(х+4)(х-2)(х-3)<0
f(х)=(х+4)(х-2)(х-3)
х=-4 х=2 х=3
-4
Ответ:
-
+
2
+
3
(-∞;-4) (2;3)
8. Решить неравенство
(10х+3)(17-х)(х-5)≥09. Работа по учебнику
Решитьх 5
а)
х 6
№ 140
<0
Решение: равносильно: (х-5)(х+6)<0
1.Рассмотрим функцию f(х)=(х-5)(х+6)
2.Нули функции х=5, х=-6
Ответ: (-6;5).
10. Работа по учебнику
Решить№ 138
Что называется областью определения?
Рассмотрим два случая:
а
У=
,в 0 ;
в
У=
а,а 0
11.
У=( х 12)( х 1)( х 9)
(х+12)(х-1)(х-9)≥0
Ответ: [-12;1] [9;+ ).
12. Самостоятельная работа
13. Найти область определения функции:
1 варианту= (2х 5)( х 17)
2 вариант
у= ( х 9)(2х 8)
14. Итог урока.
Домашнее заданиеп.9, №136, №139










 Математика
Математика








