Синтез приоритетов в неполной иерархии

1.

Лекция 3
ОТС

2.

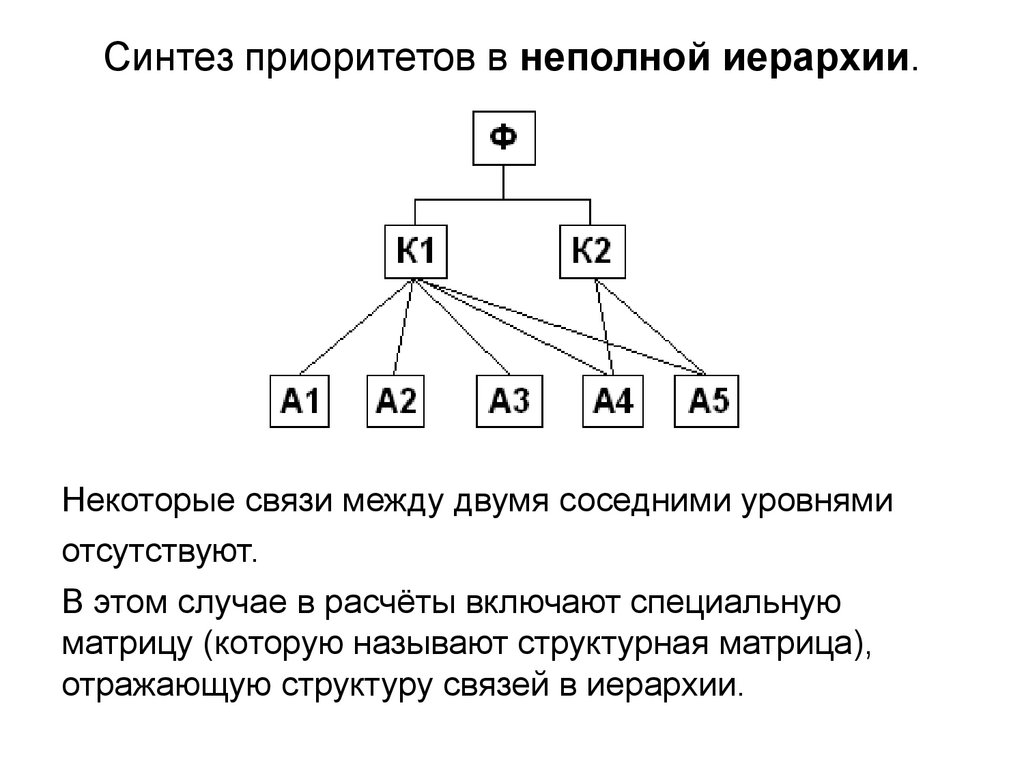
Синтез приоритетов в неполной иерархии.
Некоторые связи между двумя соседними уровнями
отсутствуют.
В этом случае в расчёты включают специальную
матрицу (которую называют структурная матрица),
отражающую структуру связей в иерархии.

3.

Структурная матрица.
К1
L=
К2
…
Кn
R1
0
...
0
K1 N
K 2 0 R2
...
0
N
... ...
... ... ...
Rn
Kn 0
0
...
N
Где Ri - число элементов-потомков элемента Ki,
N- число связей между уровнями.

4.

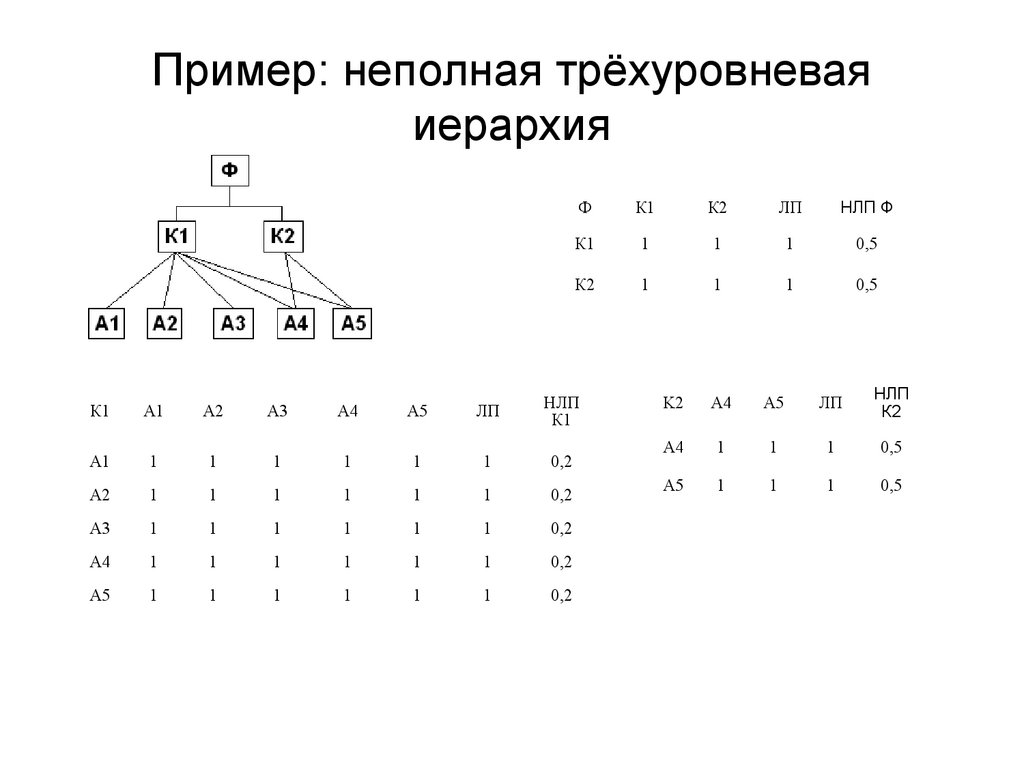
Пример: неполная трёхуровневая
иерархия
Ф
К1
К2
ЛП
НЛП Ф
К1
1
1
1
0,5
К2
1
1
1
0,5
К1
А1
А2
А3
А4
А5
ЛП
НЛП
К1
А1
1
1
1
1
1
1
0,2
А2
1
1
1
1
1
1
0,2
А3
1
1
1
1
1
1
0,2
А4
1
1
1
1
1
1
0,2
А5
1
1
1
1
1
1
0,2
K2
A4
A5
ЛП
НЛП
К2
A4
1
1
1
0,5
A5
1
1
1
0,5

5.

Строим вспомогательные матрицы
K1
А=
K2
A1 0,2 0
A2 0,2 0
A3 0,2 0
A4 0,2 0,5
A5 0,2 0,5
K1 K 2
5
K
L=
1
7
K2 0
0
2
7

6.

Синтез приоритетов
[ ]
[ ] []
0,2
0,2
ГПА= [ A]⋅[ L ]⋅НЛПц= 0,2
0,2
0,2
0,14
0,14
¿ = 0,14
0,14
0,14
0
0
5/7
∗
0
0
0,5
0,5
0
0,07
0
0,07
0,5
∗
= 0,07
0
0,5
0,14
0,14
0,14
0,14
[ ]
[
][ ]
0
0,5
∗
=
2/7
0,5

7.

Пример неэффективности метода
парных сравнений
Ф
К1
К2
ЛП
НЛП Ф
К1
A1
A2
ЛП
НЛП К1
К1
1
3
1,732
0,75
A1
1
3
1,732
0,75
К2
1/3
1
0,577
0,25
A2
1/3
1
0,577
0,25
К2
A1
A2
ЛП
НЛП К2
A1
1
1/3
0,577
0,25
A2
3
1
1,732
0,75
V(A1)=0,75*0,75+0,25*0,25=0,625
V(A2)=0,25*0,75+0,75*0,25=0,375
A1 ->A2

8.

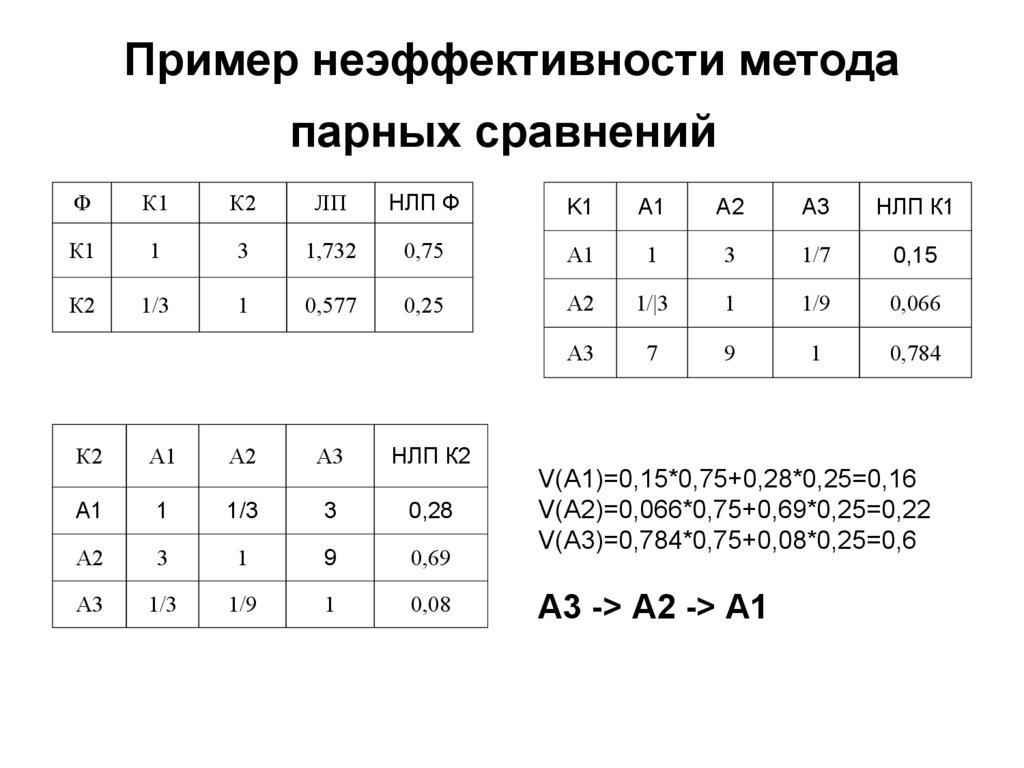
Пример неэффективности метода
парных сравнений
Ф
К1
К2
ЛП
НЛП Ф
K1
A1
A2
A3
НЛП К1
К1
1
3
1,732
0,75
A1
1
3
1/7
0,15
К2
1/3
1
0,577
0,25
A2
1/|3
1
1/9
0,066
A3
7
9
1
0,784
К2
A1
A2
A3
НЛП К2
A1
1
1/3
3
0,28
A2
3
1
9
0,69
A3
1/3
1/9
1
0,08
V(A1)=0,15*0,75+0,28*0,25=0,16
V(A2)=0,066*0,75+0,69*0,25=0,22
V(A3)=0,784*0,75+0,08*0,25=0,6
А3 -> A2 -> A1

9.

метод сравнения элементов
относительно стандарта
Метод попарных сравнений может быть неудобен
в некоторых случаях:
Когда альтернативы для сравнения поступают не
одновременно, а через промежутки времени;
Когда в задаче большое количество альтернатив
(более 8).
Кроме того, метод парных сравнений иногда
выдаёт некорректные результаты при добавлении
новых альтернатив (как в предыдущем примере).

10.

метод сравнения элементов
относительно стандарта
Стандарт устанавливает уровень качества
объекта относительно критерия качества.
Например, критерий «ликвидность» может
задавать три стандарта (уровня качества):
высокий, средний, низкий.
Основная шкала стандартов: {H, M, L}.
Дополнительная шкала: {HH, HM, ML, LL}

11.

метод сравнения элементов
относительно стандарта
Стандарты стараются делать не абстрактными, а
отождествлять их с некоторыми реальными
объектами.
Например, по критерию «надёжность» при
сравнении автомобилей можно использовать
стандарты {H, M, L}:
H — BMW
M — KIA
L — Lada.

12.

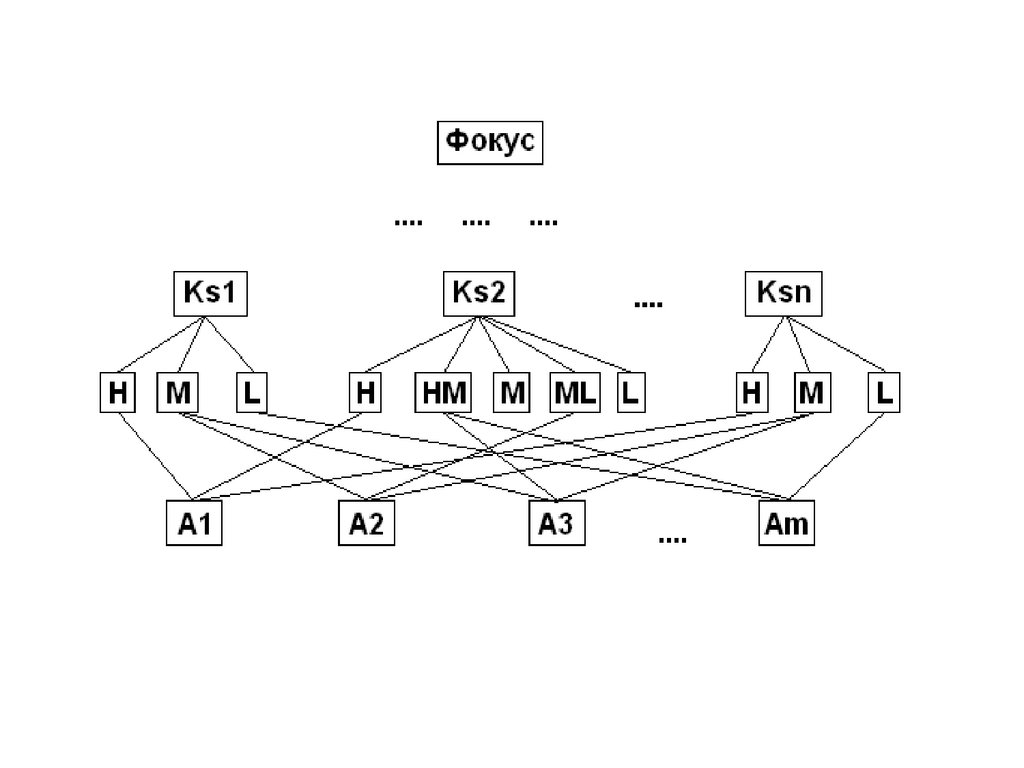
метод сравнения элементов
относительно стандарта
Стандарты помещают в иерархию, вводя для
них дополнительный уровень — между
критериями и объектами, которые сравниваются
по этим критериям (альтернативами).
Альтернативы оценивают по критериям,
связывая уровни стандартов и альтернатив.

13.

14.

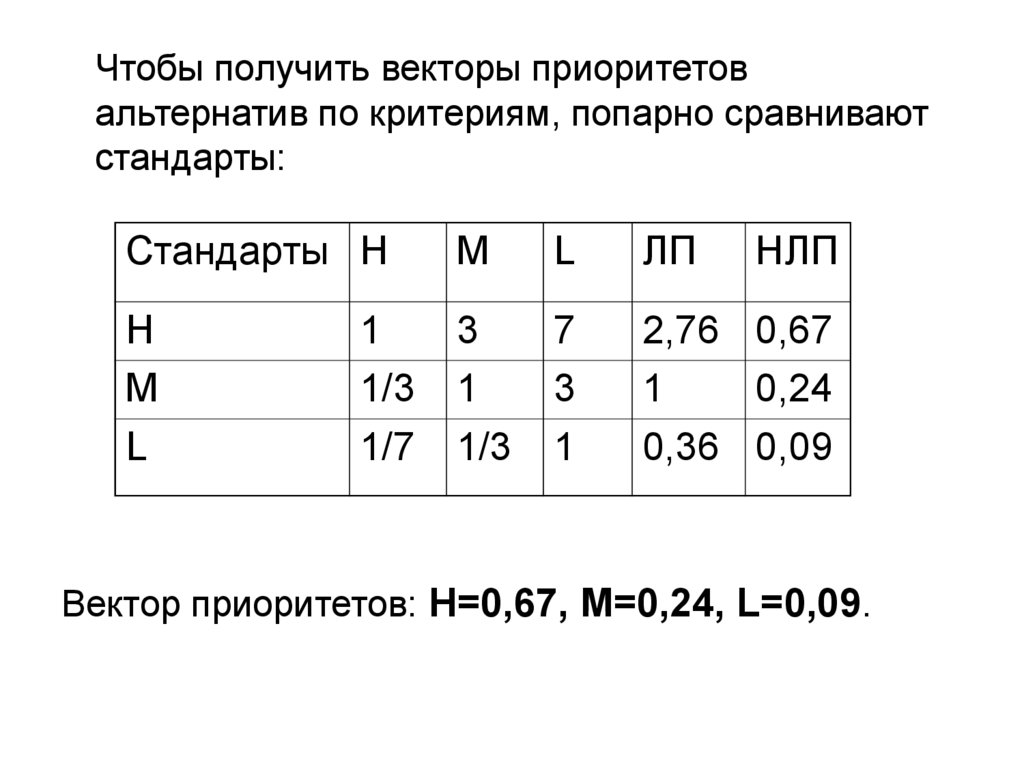
Чтобы получить векторы приоритетов
альтернатив по критериям, попарно сравнивают
стандарты:
Стандарты H
M
L
ЛП
H
M
L
3
1
1/3
7
3
1
2,76 0,67
1
0,24
0,36 0,09
1
1/3
1/7
НЛП
Вектор приоритетов: H=0,67, M=0,24, L=0,09.

15.

метод сравнения элементов
относительно стандарта
Далее составляют вектор приоритетов для
альтернатив по данному критерию. Числовые
значения стандартов, соответствующих
альтернативам задачи, записывают в вектор — т.о.
получают вектор ЛП. Затем этот вектор нормируют,
получая НЛП.
ЛП Ki
НЛП Ki
А1
H(0,67)
А2
M(0,24)
...
...
Аn
H(0,67)

16.

метод сравнения элементов
относительно стандарта
Дальнейшие расчеты по алгоритму МАИ:
после того, как получили векторы локальных
приоритетов для всех элементов иерархии,
рассчитывают глобальные приоритеты.

17.

Сравнение объектов методом
копирования
Разделим альтернативы на два
множества:
А={А1, А2, …, Аn}
В={В1, В2, …, Вm}

18.

Пример:
0,5
0,3 А1, А2, А3
0,2
Пусть для анализа поступают две новые альтернативы, свойства
которых по данному критерию полностью идентичны свойствам
альтернативы А3
0,5
0,3
0,2
0,2
0,2
0,35
0,21
0,14 А1, А2, А3, А4, А5
нормируем, получаем:
0,14
0,14

19.

Оценка согласованности иерархии
Шаг 1. Подсчет максимального собственного числа матрицы
T
парных сравнений:
max
где
e [ A] X
X - нормированный вектор локальных приоритетов (НЛП),
eT- единичный вектор-строка.
Шаг 2. Подсчитывается индекс однородности:
max n
ИО
n 1
n - это размер матрицы(размерность)

20.

Шаг 3. Рассчитывается оценка однородности.
ИО
ОО
М (ИО)
если <= 0,1 – то оценки согласованы,
если попадает в промежуток ( 0,1;0,2]
то оценки плохо согласованы,
если > 0,2 – оценки не согласованы.
n
М (ИО)
1
2
3
0
0
0,58
4
5
0,9
1,12
6
7
8
1,24
1,32
1,41
9
10
1,45
1,49

21.

Оценка согласованности иерархии
К1
К2
К4
А1
К3
К5
А2
К6
…
Аn
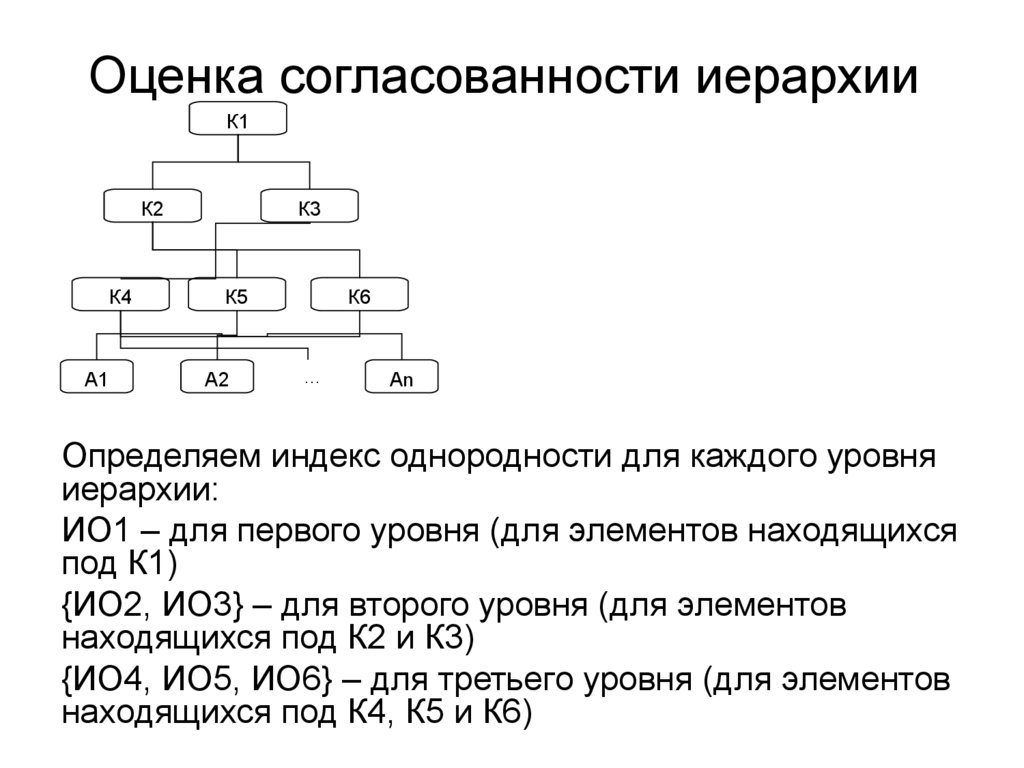
Определяем индекс однородности для каждого уровня
иерархии:
ИО1 – для первого уровня (для элементов находящихся
под К1)
{ИО2, ИО3} – для второго уровня (для элементов
находящихся под К2 и К3)
{ИО4, ИО5, ИО6} – для третьего уровня (для элементов
находящихся под К4, К5 и К6)

22.

W1, W2, W3 – векторы НЛП для элементов К1, К2 и К3.
ИОиерархии ИО1 W1
T
ИО2
T
W1 W2
ИО3
ИО4
T
W3 ИО5
ИО
6
М ИО4
T М ИО2
T
T
М ИОиерархии М ИО1 W1
W1 W2 W3 М ИО5
М ИО3
М ИО
6
ООиерархии
ИОиерархии
М ( ИОиерархии )
Однородность иерархии удовлетворительна для .
ООиерархии 0,1

23.

Методы повышения согласованности.
1.Привлечение нескольких экспертов. Оценка
выставляется:
• Путём обсуждения
• Как среднее геометрическое
• Как среднее взвешенное:
аобщ а
где
1
а
2
... а
1 2 ... n 1
2. Использование абсолютных данных.
3. Использование стандартов.
n