Похожие презентации:
Лекция 1-2. Геодезия
1.
Лекция 1. (Параметры страницы 22·22, книжная).Геодезия - наука об измерениях на поверхности земли с целью
определения ее формы и размеров, составления планов и карт, а
так же решения различных инженерных задач на местности.
Она подразделяется на:
Высшая геодезия – изучает форму и размеры земли, а также методы
высокоточного определения координат точек земной поверхности и
изображение ее на плоскости.
Топография – рассматривает методы производства топографических
съемок, для составления планов небольших участков земной поверхности .
Инженерная геодезия - рассматривает постановку и методы
геодезических работ, необходимых для проектирования, строительства
и эксплуатации инженерных сооружений.
Методы инженерной геодезии основаны на теории и способах высшей
геодезии и топографии, но имеют свои особенности связанные с
характером строительства.
Фототопография – основана на получении топографических планов с
использованием аэрофотоснимков.
2.
Геодезия тесно связана с такими науками как математика, физика,астрономия, география, геология и геоморфология.
История геодезии начинается за много веков до нашей эры. Геодезические
работы проводились в древнем Египте, Греции, Риме.
В России совершенная постановка геодезических работ началась при
Петре 1. В 1739 году был утвержден географический департамент при
Российской академии наук.
ФОРМА ЗЕМЛИ.
Физическая поверхность земли в геометрическом отношении имеет
сложную форму. При определении формы окружающих нас предметов
их обычно сравнивают с геометрически правильными телами.
Если предположить, что земля находится в состоянии покоя и плотность ее
равномерно распределяется по всей массе, то она имела бы форму шара.
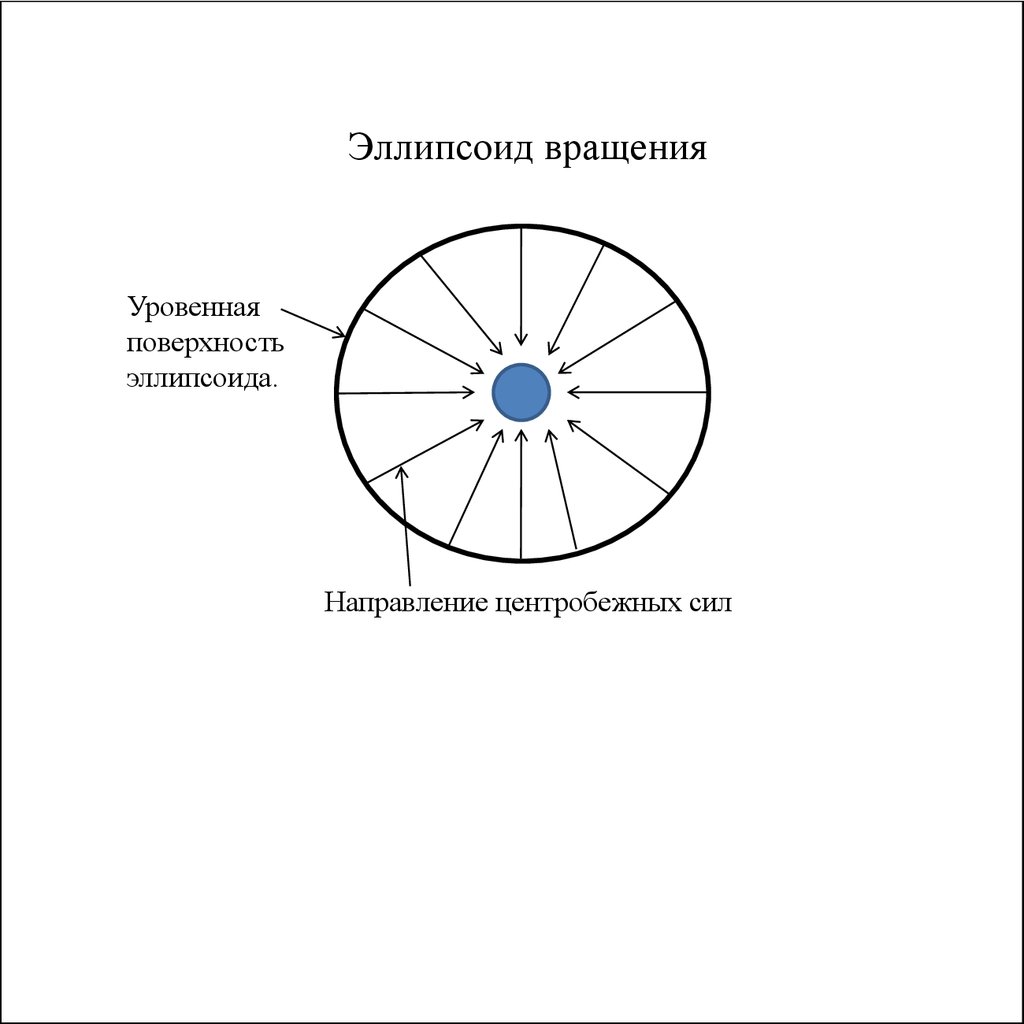
Под действием центробежной силы вызванной вращением вокруг оси с
постоянной скоростью земля бы приобрела форму, сплющенную по
направлению к полюсам, то есть форму сфероида или эллипсоида.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
Эллипсоид вращенияНаправление центробежных сил
17.
Поверхность такого эллипсоида была бы всюду горизонтальной, анаправление силы тяжести было бы перпендикулярным (нормальным)
к ней, т.е. направление силы тяжести совпадало бы в каждой точке с
нормалью к поверхности эллипсоида.
Такие поверхности называются уровенными, и поверхность такого
эллипсоида была бы уровенной.
18.
Эллипсоид вращенияУровенная
поверхность
эллипсоида.
Направление центробежных сил
19.
Однако земля неоднородна, она состоит из нескольких слоев, плотностькоторых примерно одинакова в каждом слое. Теоретические расчеты
показывают, что и в этом случае земля имела бы форму эллипсоида, но
с другим коэффициентом сжатия.
Однако самый верхний слой (земная кора ) мощностью от 6 до 70 км.,
средняя 40 км., закономерностей в распределении плотностей не имеет
и строение его весьма сложно. Таким образом, внешняя
(топографическая) поверхность земли имеет сложную геометрическую
форму. Под действием неравномерно, расположенных масс в земной коре
изменяется направление сил притяжения, а следовательно и сил тяжести.
Уровенная поверхность земли отступает от поверхности эллипсоида,
становится сложной и неправильной в геометрическом отношении,
она совпадает с невозмущенной (спокойной) поверхностью океанов и
морей и не определяется, какой-либо из известных аналитических
форм. Ей присвоено название геоид.
Геоидом называется уровенная поверхность, совпадающая с
поверхностью океанов и морей при спокойном состоянии водных масс
и мысленно продолженных под материками, таким образом, что бы
направление силы тяжести пересекало бы ее под прямым углом.
Наибольшее отступление геоида от эллипсоида незначительное и не
превышает 100-150 км., поэтому фигурой наиболее приближенной к
геоиду является эллипсоид вращения.
20.
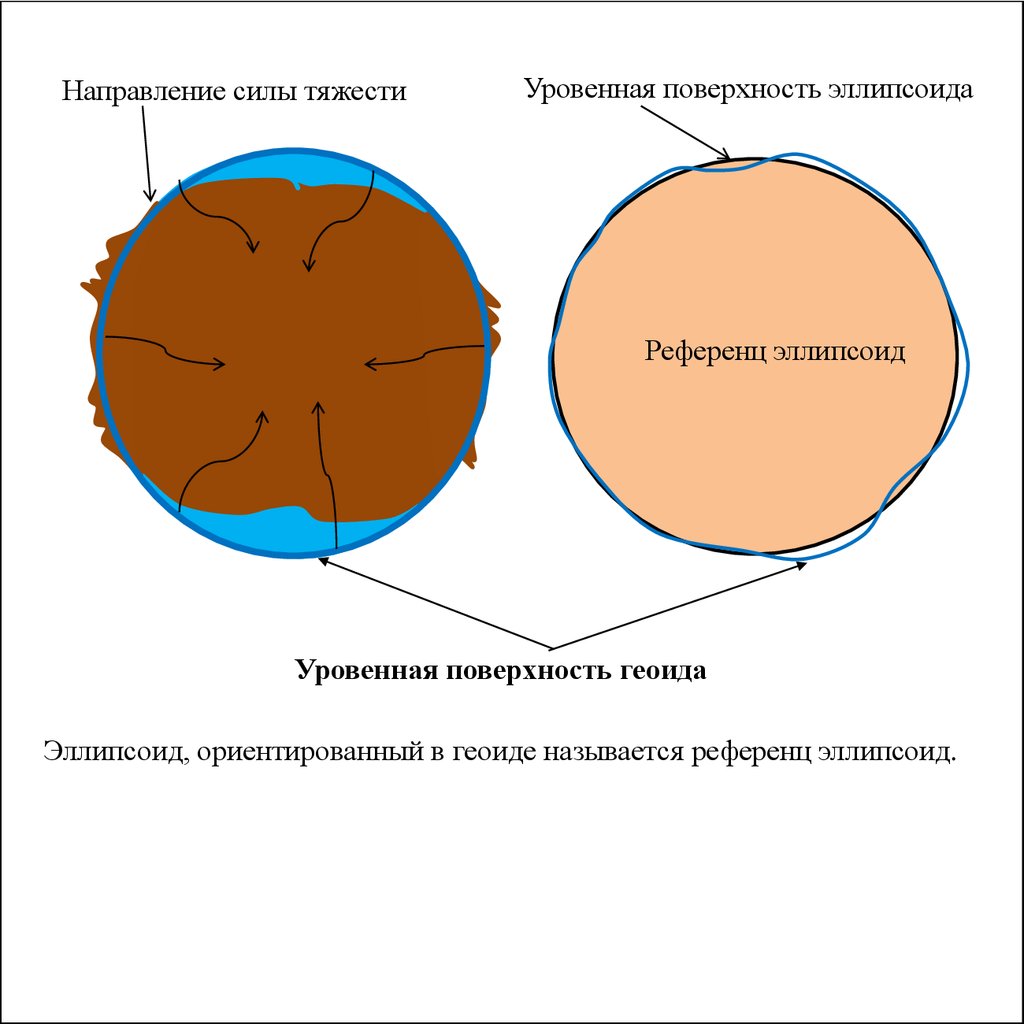
Направление силы тяжестиУровенная поверхность эллипсоида
Референц эллипсоид
Уровенная поверхность геоида
Эллипсоид, ориентированный в геоиде называется референц эллипсоид.
21.
Эллипсоид Красовского.Его размеры и форма характеризуется следующими параметрами:
осями (а) и (b) , и (α) - коэффициентом полярного сжатия. В СССР
размеры земного эллипсоида были получены в 1940 году советскими
учеными Красовским и Изотовым. Который имеет параметры :
а = 6378,245 км., α = 1:298,3.
a
b
СИСТЕМЫ КООРДИНАТ.
В геодезии принимаются различные системы координат.
1. Геодезическая система координат. В этой системе за основу
координационной поверхности принимается поверхность референц
эллипсоида, а за основные координатные линии геодезические
параллели и меридианы.
Геодезическим меридианом называется сечение эллипсоида плоскостью
проходящей через точку на его поверхности и малую полярную ось.
Геодезической параллелью называют сечения эллипсоида плоскостью
проходящей через точку на его поверхности и перпендикулярной к малой
оси. Параллель, проходящая через центр эллипсоида, называется
экватором.
22.
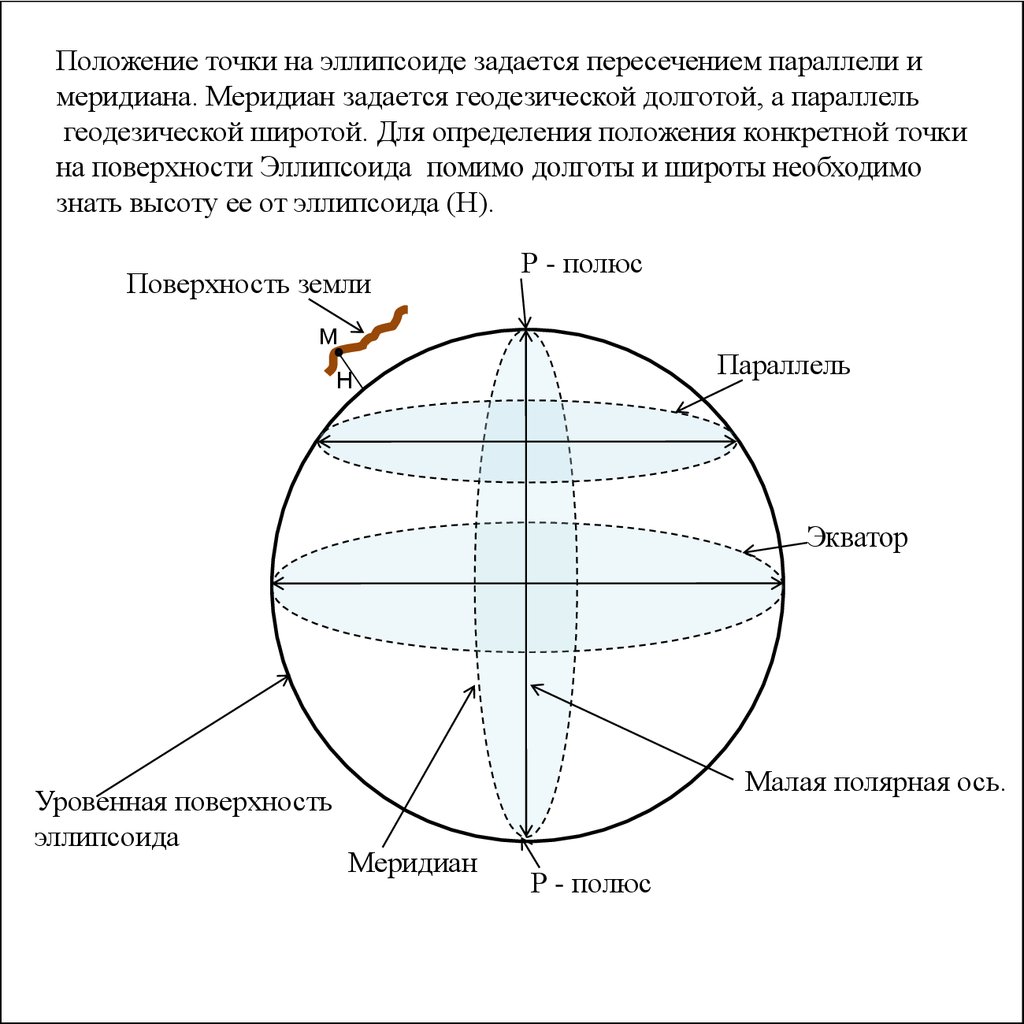
Положение точки на эллипсоиде задается пересечением параллели имеридиана. Меридиан задается геодезической долготой, а параллель
геодезической широтой. Для определения положения конкретной точки
на поверхности Эллипсоида помимо долготы и широты необходимо
знать высоту ее от эллипсоида (Н).
Поверхность земли
Р - полюс
м
Параллель
Н
Экватор
Уровенная поверхность
эллипсоида
Малая полярная ось.
Меридиан
Р - полюс
23.
За начальную отсчетную поверхность принимается уровень моря.Относительно ее и принимают высоты точек поверхности земли,
называемые абсолютными. В нашей стране за начальную точку отсчета
принят нуль Крондштадского футштока, близко совпадающий с
уровнем моря.
Астрономическая система координат отличается от геодезической на
3 -4 секунды и вместе с геодезической входит в понятие географической
системы координат, которой и пользуются в геодезии, проводя
измерения геодезическими методами.
24.
Если размеры участка земной поверхности позволяют не приниматьво внимание сферичность земли, то пользуются плоской системой
Декартовых координат, которую образуют две перпендикулярные
линии, лежащие в горизонтальной плоскости. Пересечение прямых
в т. 0, принимается за начало отсчета координат. Четверти нумеруются
по ходу часовой стрелки, Северо-Восточная четверть – первая.
С
+X
м
lV
l
0
-Y З
В +Y
lll
ll
-X
Ю
25.
Для перехода от частной системы координат к географическойнеобходимо знать точные координаты точки 0 и угол между
положительным направлением оси абсцисс Х и северным
направлением меридиана.
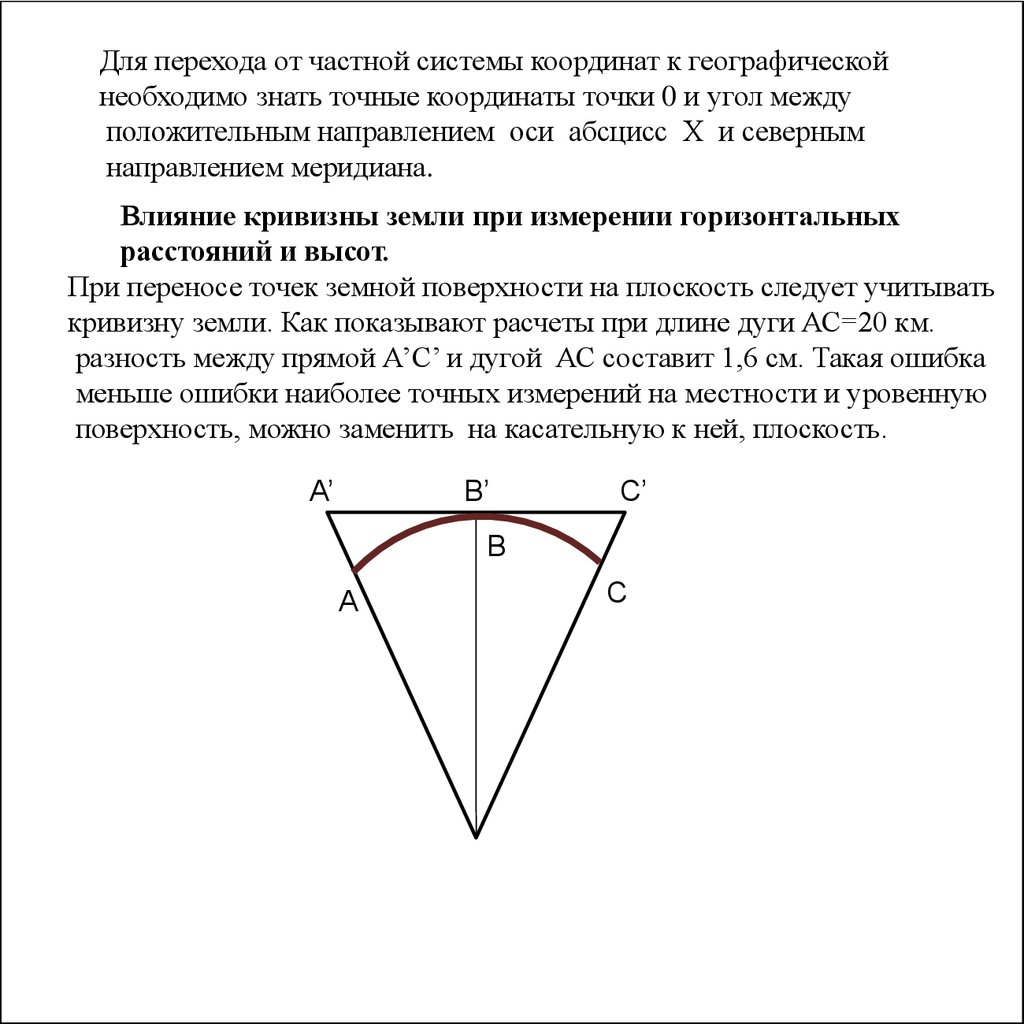
Влияние кривизны земли при измерении горизонтальных
расстояний и высот.
При переносе точек земной поверхности на плоскость следует учитывать
кривизну земли. Как показывают расчеты при длине дуги АС=20 км.
разность между прямой А’С’ и дугой АС составит 1,6 см. Такая ошибка
меньше ошибки наиболее точных измерений на местности и уровенную
поверхность, можно заменить на касательную к ней, плоскость.
A’
B’
C’
B
A
C
26.
Сложнее обстоит дело с определением высот точек. Расчеты показывают,что уже при длине дуги в 500 метров, ошибка составит 2 см. И эту ошибку
необходимо учитывать, так как инженерные работы требуют точности
порядка 2см. на 1 км. расстояния. При менее точных горизонтальных
измерениях длина дуги АС допускается до 50 км. Изображение такого
участка на бумаге в горизонтальной проекции в уменьшенном
изображении называется планом местности.
Для изображения значительных частей земной поверхности на
плоскость принимают специальные проекции, дающие возможность
переносить на плоскость положение точек земной поверхности по
математическим законам и определять их в плоской системе координат
Х, У. В нашей стране за основу системы координат принята проекция,
предложенная немецкими учеными Гауссом и Крюгером и получившая,
наименование Гаусса-Крюгера.
0
0
0
0
27.
Согласно этой проекции земной шар разделен 3 или 6 градусные зонывдоль меридианов, нумерация которых ведется с запада на восток,
начиная от Гринвичского меридиана, принятого за ноль.
Далее каждый сегмент разворачивается на плоскость, где осевой
меридиан изображается прямой линией без искажения, т.е. точным
сохранением его длины.
Экватор в каждом сегменте также изображается прямой линией
перпендикулярной осевому меридиану. За начало отсчета координат
принимается пересечение экватора и осевого меридиана. Искажение
длин линий в проекции Гаусса-Крюгера возрастают по мере удаления
от осевого меридиана и могут достигать величины порядка 1:1500 в
шестиградусной зоне и 1:6000 в трехградусной.
В инженерно-геодезических работах и при крупномасштабных съемках
такие искажения необходимо учитывать, либо применять частную
систему координат с осевым меридианом, проходящим через середину
участка работ. Система координат в каждой зоне (сегменте) одинакова.
Все географические карты на территории бывшего СССР, стран
восточной и части стран западной Европы составлены в проекции
Гаусса-Крюгера.
28.
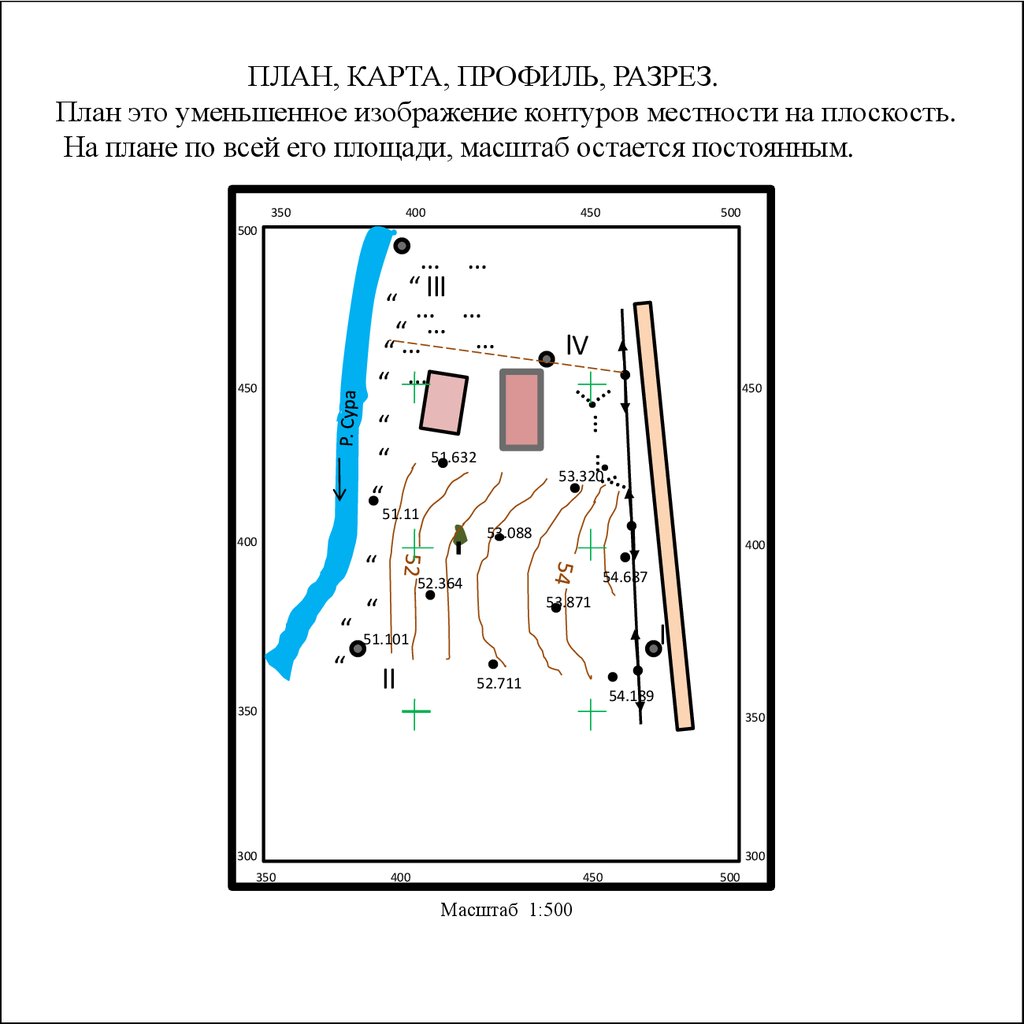
ПЛАН, КАРТА, ПРОФИЛЬ, РАЗРЕЗ.План это уменьшенное изображение контуров местности на плоскость.
На плане по всей его площади, масштаб остается постоянным.
350
400
450
450
lV
450
… …
… …
“ lll
“ … …
“… … …
“
“ …
“
“ 51.632
“51.11
500
500
500
53.320
53.088
400
“
“
“
“
400
54.687
52.364
53.871
l
51.101
ll
52.711
54.189
350
350
300
350
300
400
450
Масштаб 1:500
500
29.
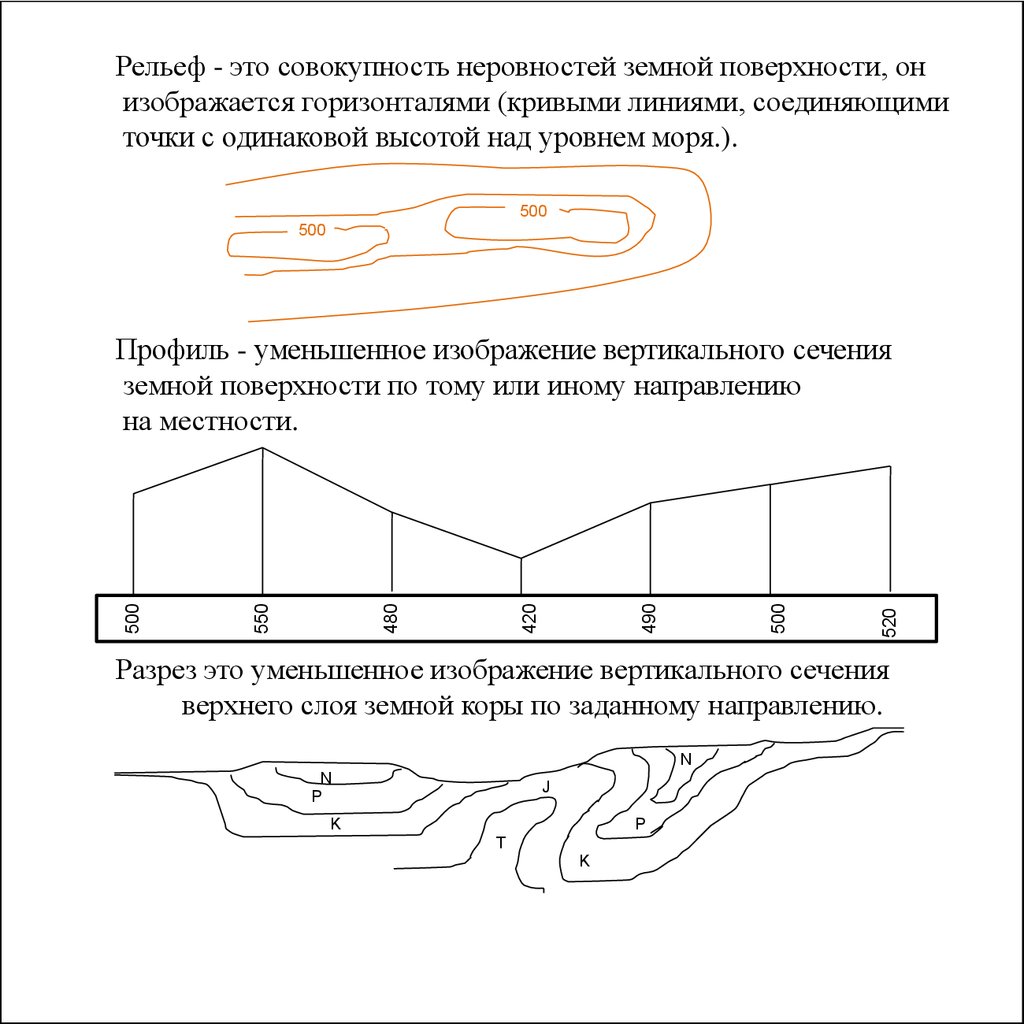
Рельеф - это совокупность неровностей земной поверхности, онизображается горизонталями (кривыми линиями, соединяющими
точки с одинаковой высотой над уровнем моря.).
500
500
520
500
490
420
480
550
500
Профиль - уменьшенное изображение вертикального сечения
земной поверхности по тому или иному направлению
на местности.
Разрез это уменьшенное изображение вертикального сечения
верхнего слоя земной коры по заданному направлению.
N
N
P
J
K
P
T
K
30.
МАСШТАБ.Масштаб это степень уменьшения горизонтальных отрезков линий
местности при переносе их на план. Существуют численный, линейный
и поперечный масштабы. Численный масштаб представляет собой простую
дробь, в числителе которой стоит единица, а в знаменателе значение
уменьшения линий местности при переносе их на план. На планах
численный масштаб подписывается как 1:500; 1:5000; 1:50000 и т. д.
Численный масштаб число отвлеченное, не имеющее размерности,
что позволяет вести измерения в любой системе мер. Чем больше дробь,
тем крупнее масштаб и наоборот.
Для упрощения работы пользуются линейным масштабом, являющимся
графическим изображением численного в той или иной системе мер.
Для его построения на прямой откладывается несколько отрезков
одинаковой длины, например 2 см. Длина такого отрезка называется
основанием масштаба. Число метров соответствующее основанию
масштаба, называется величиной линейного масштаба. Рассчитано, что
человеческий глаз способен различать две точки на расстоянии 0,1 мм.
Величина отрезка местности соответствующая 0,1мм., называется
точностью масштаба карты. Так для масштаба 1:1000 точность масштаба
равняется 0,1 м.
20
2 см.
0
20
40
60
80
100
31.
Необходимо отметить, что с помощью численного масштаба труднопроизводить построения с точностью менее 1 мм. Для этого используют
поперечный масштаб. Для этой цели на прямой откладывают несколько
отрезков (оснований) длиной 2 см., из точек пересечения восстанавливаем
перпендикуляры, высота которых произвольна (желательно кратная
делению на 10).
Делим вертикальную линию на десять частей (m) и из пересечений
проведем прямые параллельные основанию.
32.
33.
34.
Крайний левый квадрат делим на десять частей (n) по горизонтали вверхней и нижней частях.
35.
Соединив концы отрезков аналогично показанному на рисунке, получаемсетку поперечного масштаба.
Наклонные линии называются трансверсалями.
36.
Соединив концы отрезков аналогично показанному на рисунке, получаемсетку поперечного масштаба.
37.
Из подобия треугольников ОАВ и Оаb можно видеть, что:аb /АВ = оb/ ОВ = 1/ 10 сд / АВ = од / ОВ = 2 / 10.
По построению АВ равно 1/10 от основания масштаба, следовательно
наименьшее деление ab равно 1/100 от основания масштаба.
Такой масштаб называется сотенным. Он гравируется на металлических
пластинах и используется при построении планов и карт.
А
В
e
f
c
d
а
b
O
20
0
20
40
60
38.
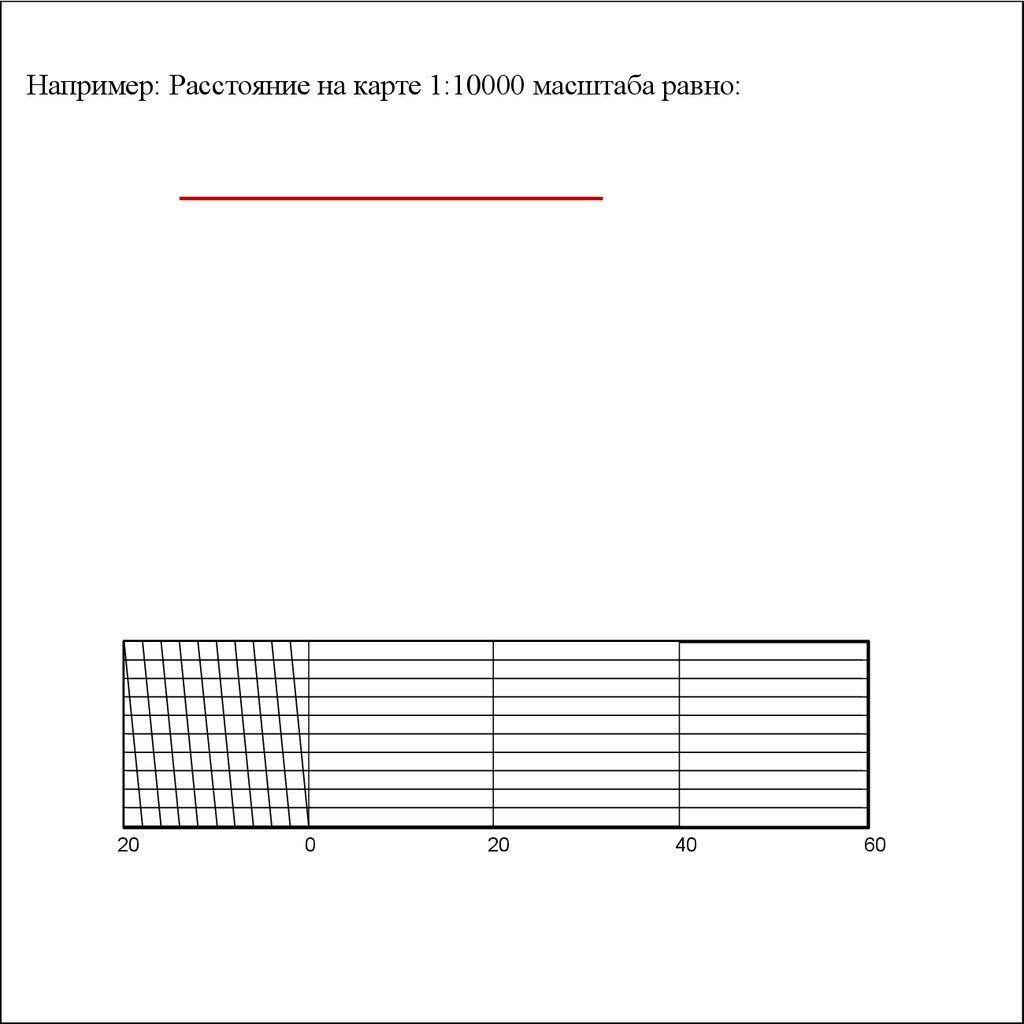
Например: Расстояние на карте 1:10000 масштаба равно:20
0
20
40
60
39.
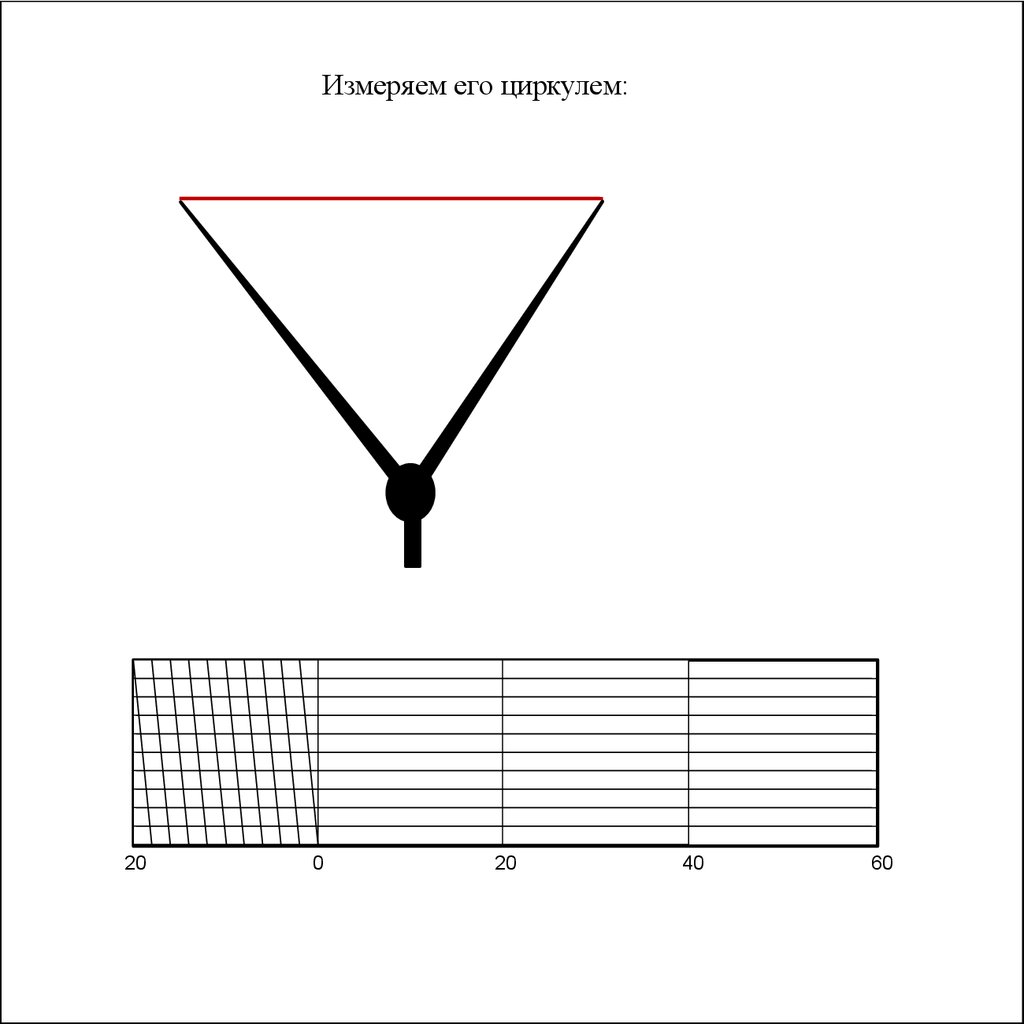
Измеряем его циркулем:20
0
20
40
60
40.
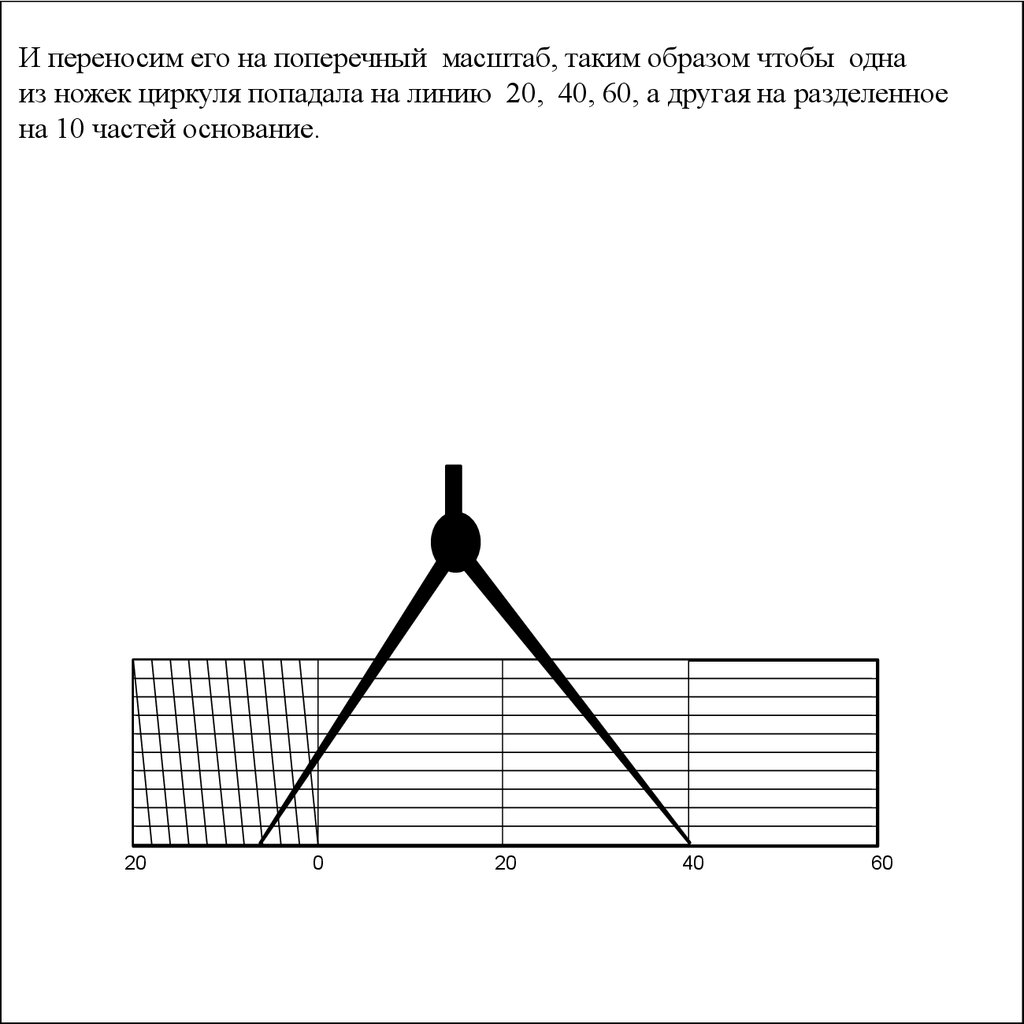
И переносим его на поперечный масштаб, таким образом чтобы однаиз ножек циркуля попадала на линию 20, 40, 60, а другая на разделенное
на 10 частей основание.
20
0
20
40
60
41.
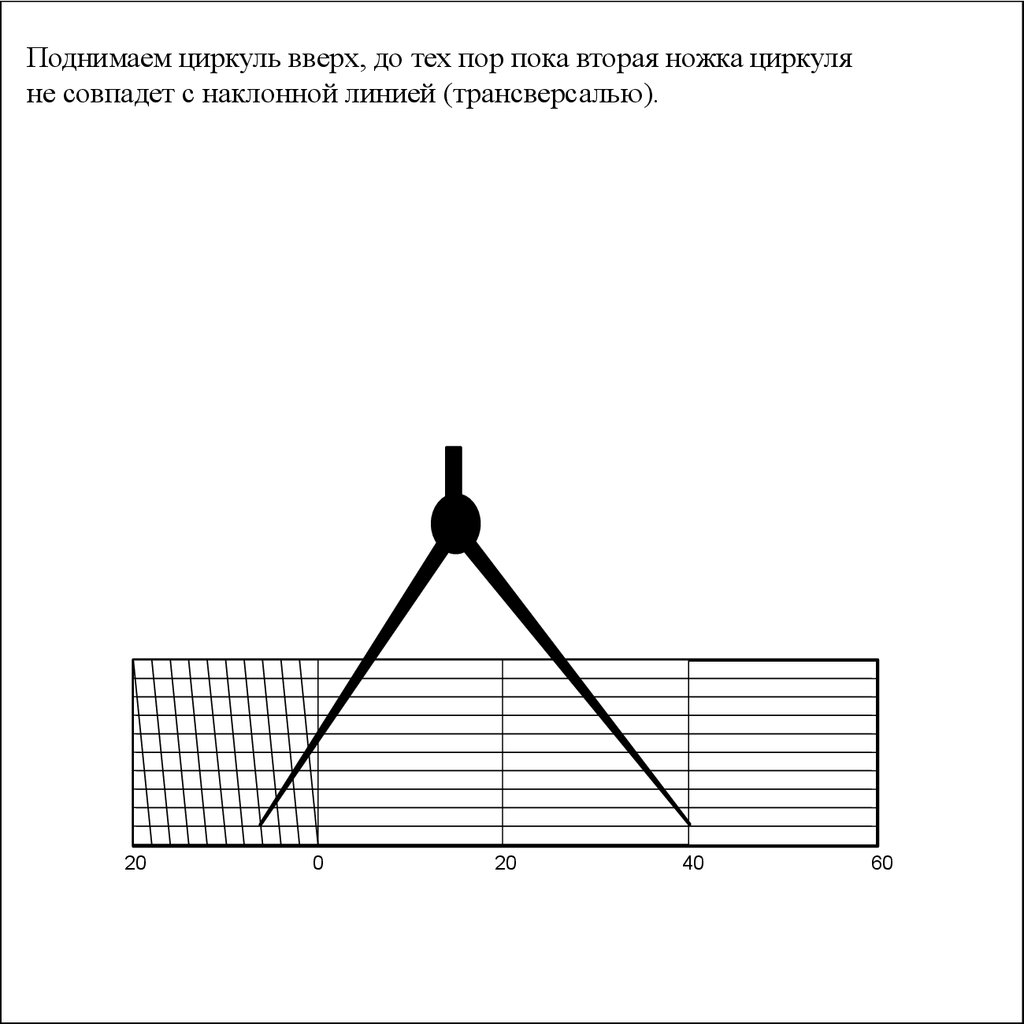
Поднимаем циркуль вверх, до тех пор пока вторая ножка циркуляне совпадет с наклонной линией (трансверсалью).
20
0
20
40
60
42.
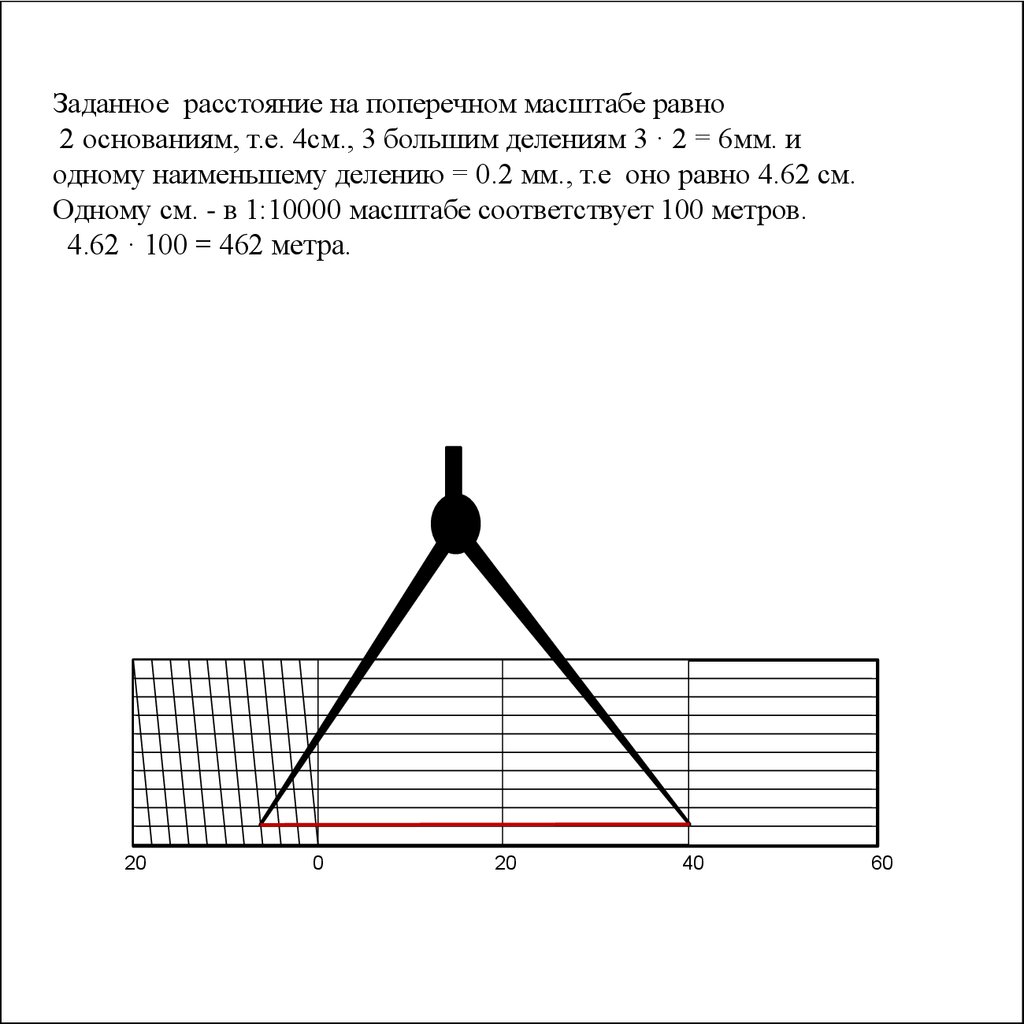
Заданное расстояние на поперечном масштабе равно2 основаниям, т.е. 4см., 3 большим делениям 3 · 2 = 6мм. и
одному наименьшему делению = 0.2 мм., т.е оно равно 4.62 см.
Одному см. - в 1:10000 масштабе соответствует 100 метров.
4.62 · 100 = 462 метра.
20
0
20
40
60
43.
КАРТА.Изображение значительных территорий земной поверхности с учетом
кривизны земли на плоскости называется картой. При построении
карты предполагается, что поверхность земли сначала наносится
на глобус, а затем с его поверхности переносится на плоскость.
Этот перенос сводится к переносу параллелей и меридианов с глобуса
на плоскость, называемой картографической сеткой, внутри которой
наносятся контуры местности и рельеф.
Математический закон построения картографической сетки на
плоскости называется картографической проекцией. Существенным
отличием карты от плана является закономерное изменение масштаба
карты от точки к точке, тогда как на плане масштаб постоянен.
На карте имеется направление (вдоль одного из меридианов или
параллелей где масштаб постоянен), такой масштаб называется
главным и равен масштабу глобуса. В остальных частях карты
масштаб отличается от главного и называется частным.
Общегеографические карты масштаба 1:300000 и крупнее
называются топографическими. Карты масштаба 1:100000 и крупнее
получают в результате съемки местности.
44.
ОРИЕНТИРОВАНИЕ ЛИНИЙ.Ориентировать линию на местности значить найти ее направление
относительно меридиана. В качестве углов определяющих направление
линий служат азимуты, дирекционные углы и румбы.
Азимутом называется горизонтальный угол, отсчитываемый от
северного конца меридиана до заданного направления. Они
изменяются от 0 до 360 градусов. Азимут называется истинным,
если он отсчитывается от истинного меридиана. Меридианы не
параллельны друг другу. Угол между направлением двух меридианов
в данных двух точках называется сближением γ меридианов и
обозначается через направление истинного меридиана, вычисляется
путем астрономических наблюдений.
На практике часто пользуются магнитными азимутами. Направление
магнитного меридиана определяется направлением магнитной стрелки.
Магнитный меридиан, как правило, не совпадает с истинным, так как
магнитные полюса смещены относительно истинных полюсов земли.
Угол между истинным меридианом и магнитным называется склонением
магнитной стрелки δ. Магнитный азимут равен Ам = Аист. - δ
45.
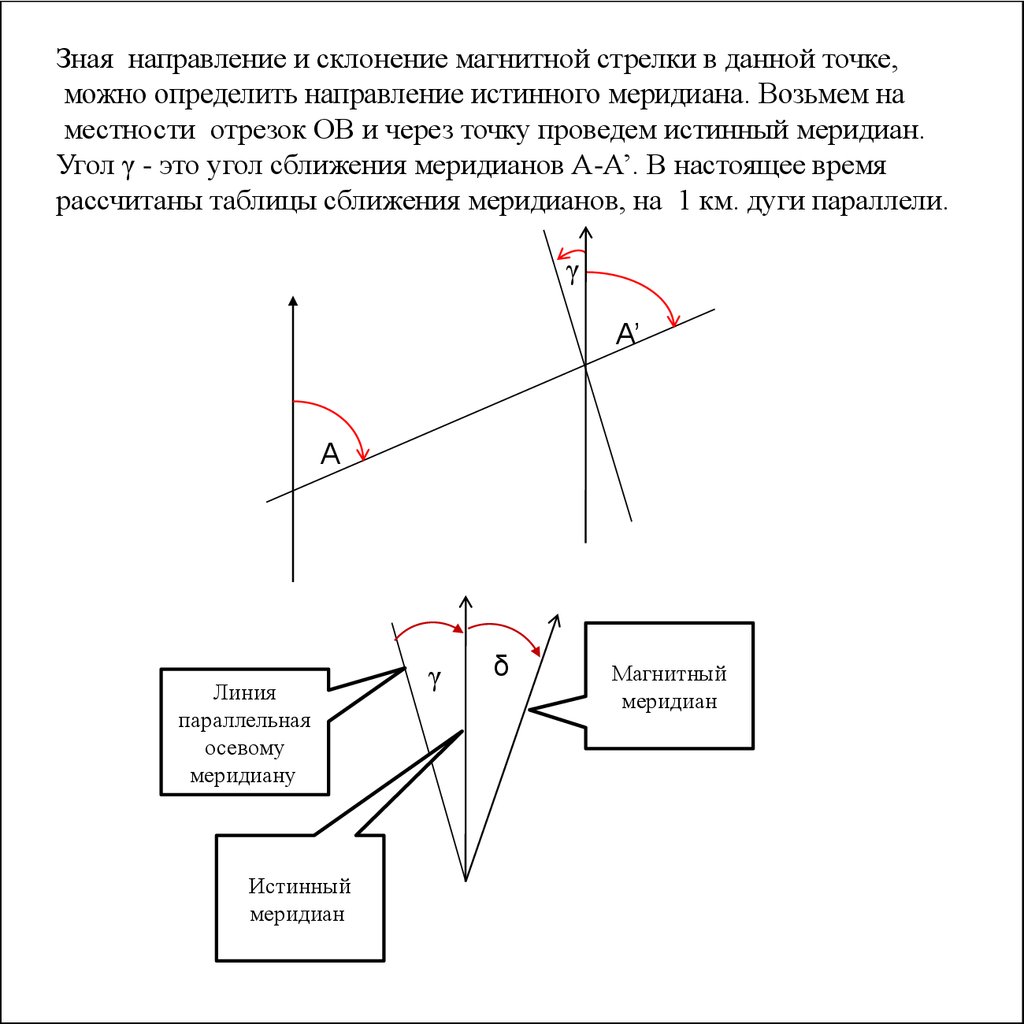
Зная направление и склонение магнитной стрелки в данной точке,можно определить направление истинного меридиана. Возьмем на
местности отрезок ОВ и через точку проведем истинный меридиан.
Угол γ - это угол сближения меридианов А-А’. В настоящее время
рассчитаны таблицы сближения меридианов, на 1 км. дуги параллели.
γ
А’
А
Линия
параллельная
осевому
меридиану.
Истинный
меридиан.
γ
δ
Магнитный
меридиан
46.
Дирекционный угол - это горизонтальный угол, отсчитываемый отсеверного направления осевого меридиана или линии, параллельной
ему, до заданного направления, по часовой стрелке. В отличие от
азимутов, дирекционный угол постоянен на протяжение всего
направления. При определении дирекционного угла на местности
необходимо знать значение истинного азимута и величину сближения
меридианов γ, тогда α = Аист. + γ. Значение величины γ подписывается под
южной стороной рамок топографических карт.
Румб это острый угол отсчитываемый от северного или южного конца
меридиана по или против часовой стрелки, до заданного направления. Так
как румбы могут иметь одинаковые значения в разных четвертях, то перед
численным значением румба указывается буквенное значение четверти.
l четверть – СВ, ll четверть – ЮВ, lll четверть – ЮЗ, lVчетверть – СЗ.
Румбы еще называют таблитчатыми углами, так как все геодезические
таблицы рассчитаны от 0° до 90°.
47.
СООТНОШЕНИЕ ДИРЕКЦИОННЫХ УГЛОВ И РУМБОВ.В первой четверти дирекционный угол α равен румбу r.
С
α
l
r
В
З
Ю
Наименов.
l - СВ
Дир. угол α
α=r
Румб r
r=α
ll – ЮВ
lll - ЮЗ
lV - CЗ
48.
СООТНОШЕНИЕ ДИРЕКЦИОННЫХ УГЛОВ И РУМБОВ.Во второй четверти дирекционный угол α = 180° - r.
С
α
l
В
З
r
ll
Ю
Наименов.
l - СВ
ll – ЮВ
Дир. угол α
α=r
α = 180°- r
Румб r
r=α
r=180° - α
lll - ЮЗ
lV - CЗ
49.
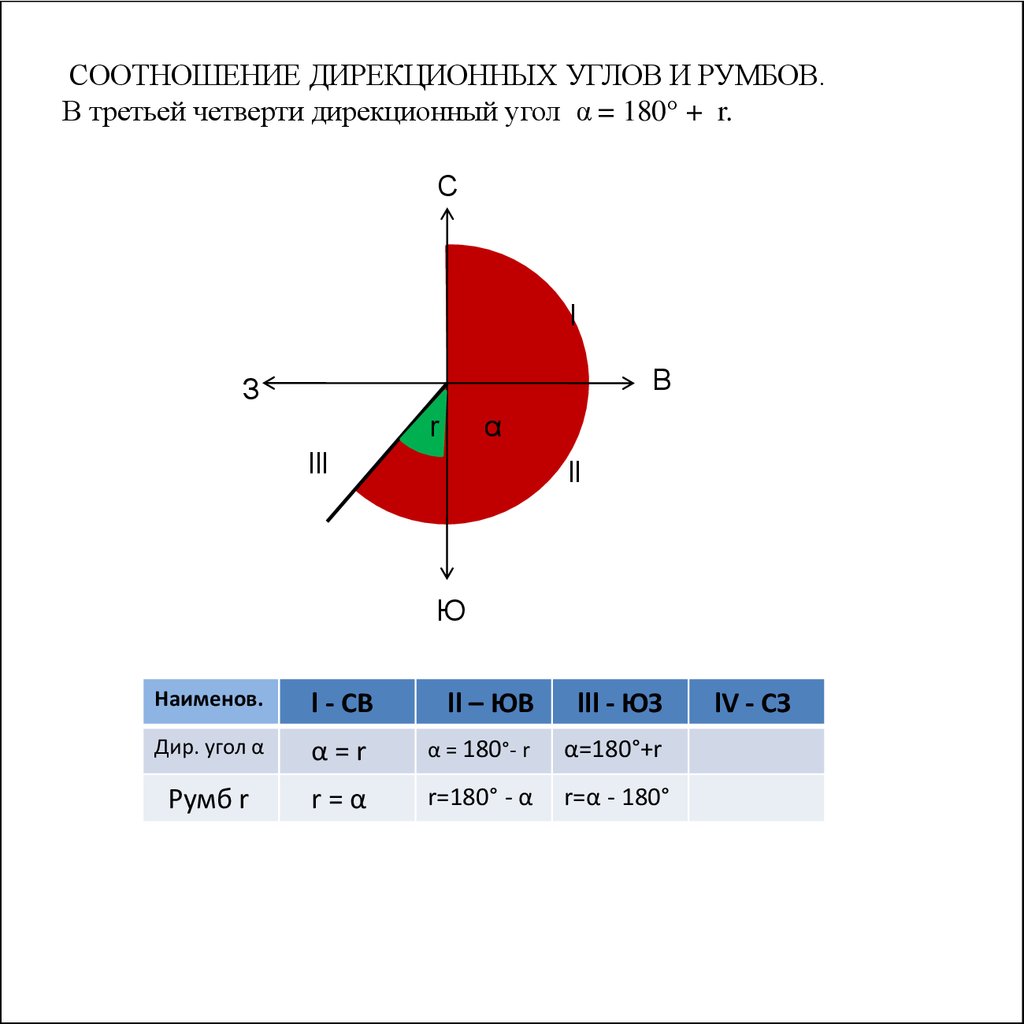
СООТНОШЕНИЕ ДИРЕКЦИОННЫХ УГЛОВ И РУМБОВ.В третьей четверти дирекционный угол α = 180° + r.
С
l
В
З
α
r
lll
ll
Ю
Наименов.
l - СВ
ll – ЮВ
lll - ЮЗ
Дир. угол α
α=r
α = 180°- r
α=180°+r
Румб r
r=α
r=180° - α
r=α - 180°
lV - CЗ
50.
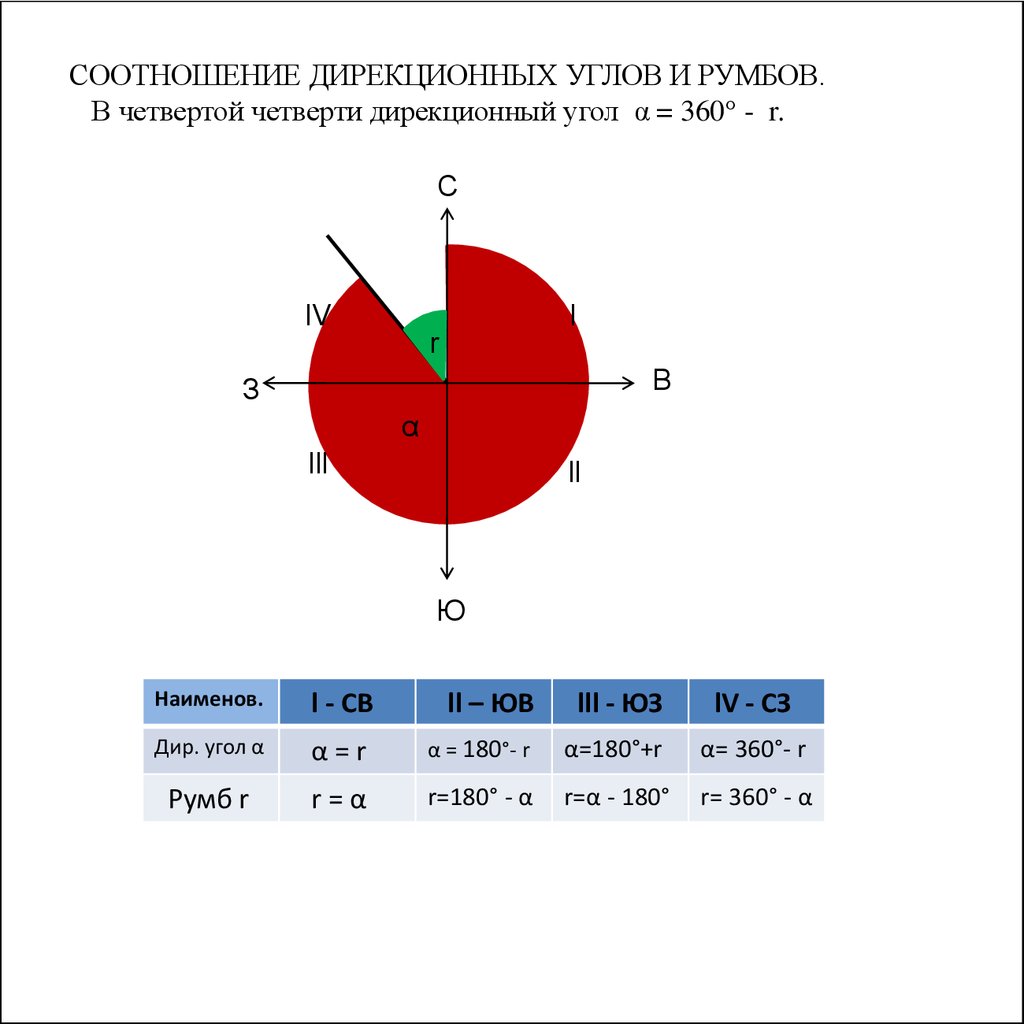
СООТНОШЕНИЕ ДИРЕКЦИОННЫХ УГЛОВ И РУМБОВ.В четвертой четверти дирекционный угол α = 360° - r.
С
lV
l
r
В
З
α
lll
ll
Ю
Наименов.
l - СВ
ll – ЮВ
lll - ЮЗ
lV - CЗ
Дир. угол α
α=r
α = 180°- r
α=180°+r
α= 360°- r
Румб r
r=α
r=180° - α
r=α - 180°
r= 360° - α
51.
ПРЯМАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧА.Даны координаты первой точки (Х1 и У1), горизонтальное расстояние от
первой до второй точки d1-2 и дирекционный угол α1-2 линии 1- 2.
Требуется определить координаты точки 2 (Х2 и У2).
2
1
X1
α1-2
Y1
52.
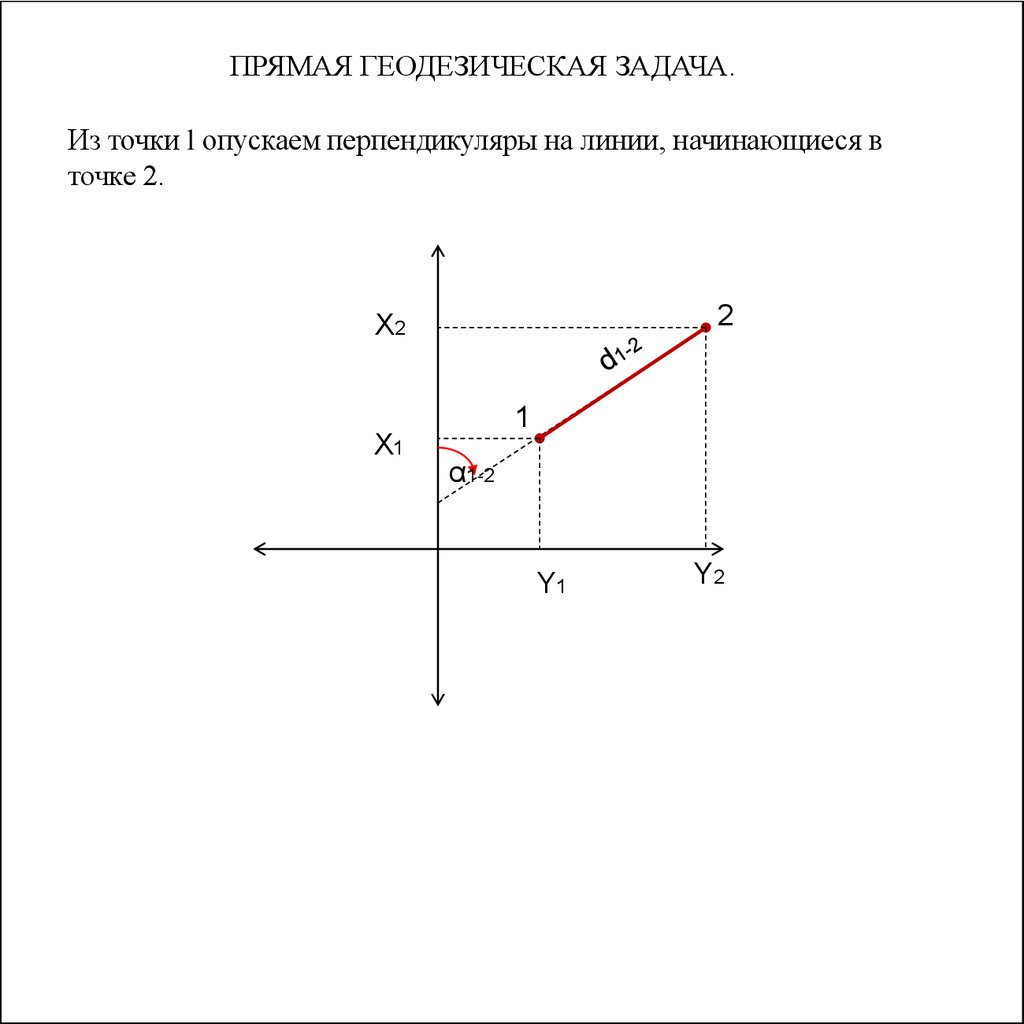
ПРЯМАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧА.Из точки l опускаем перпендикуляры на линии, начинающиеся в
точке 2.
2
Х2
1
X1
α1-2
Y1
Y2
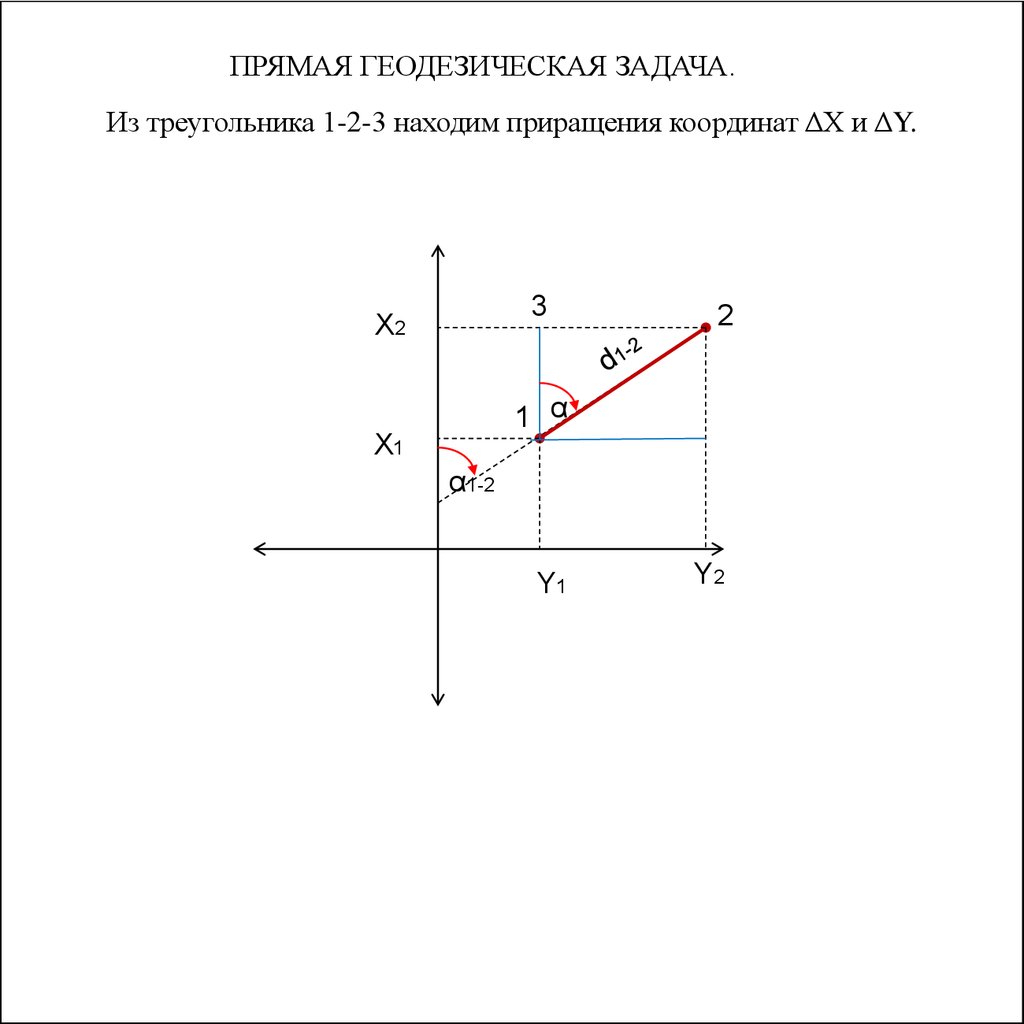
53.
ПРЯМАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧА.Из треугольника 1-2-3 находим приращения координат ΔХ и ΔY.
3
Х2
2
1 α
X1
α1-2
Y1
Y2
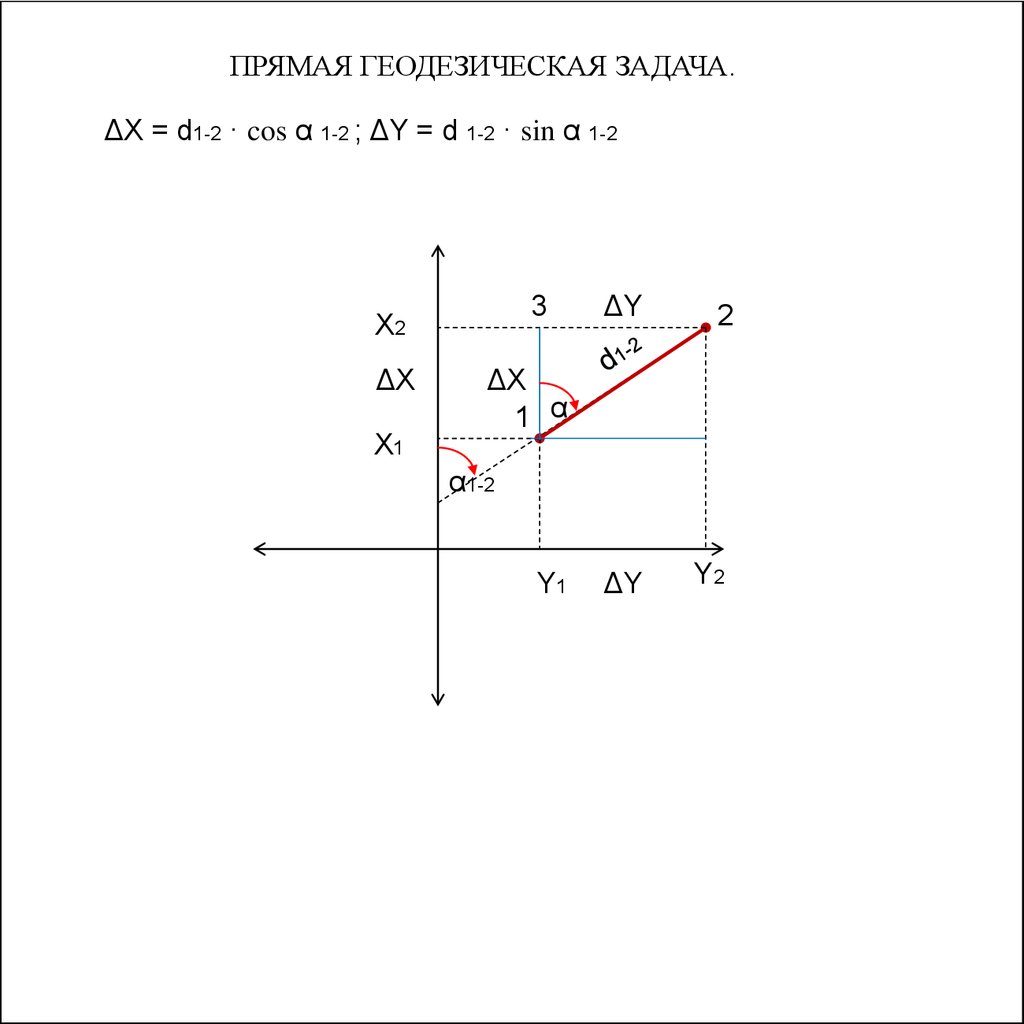
54.
ПРЯМАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧА.ΔX = d1-2 · cos α 1-2 ; ΔY = d 1-2 · sin α 1-2
3
Х2
ΔХ
ΔY
2
ΔХ
1 α
X1
α1-2
Y1
ΔY
Y2
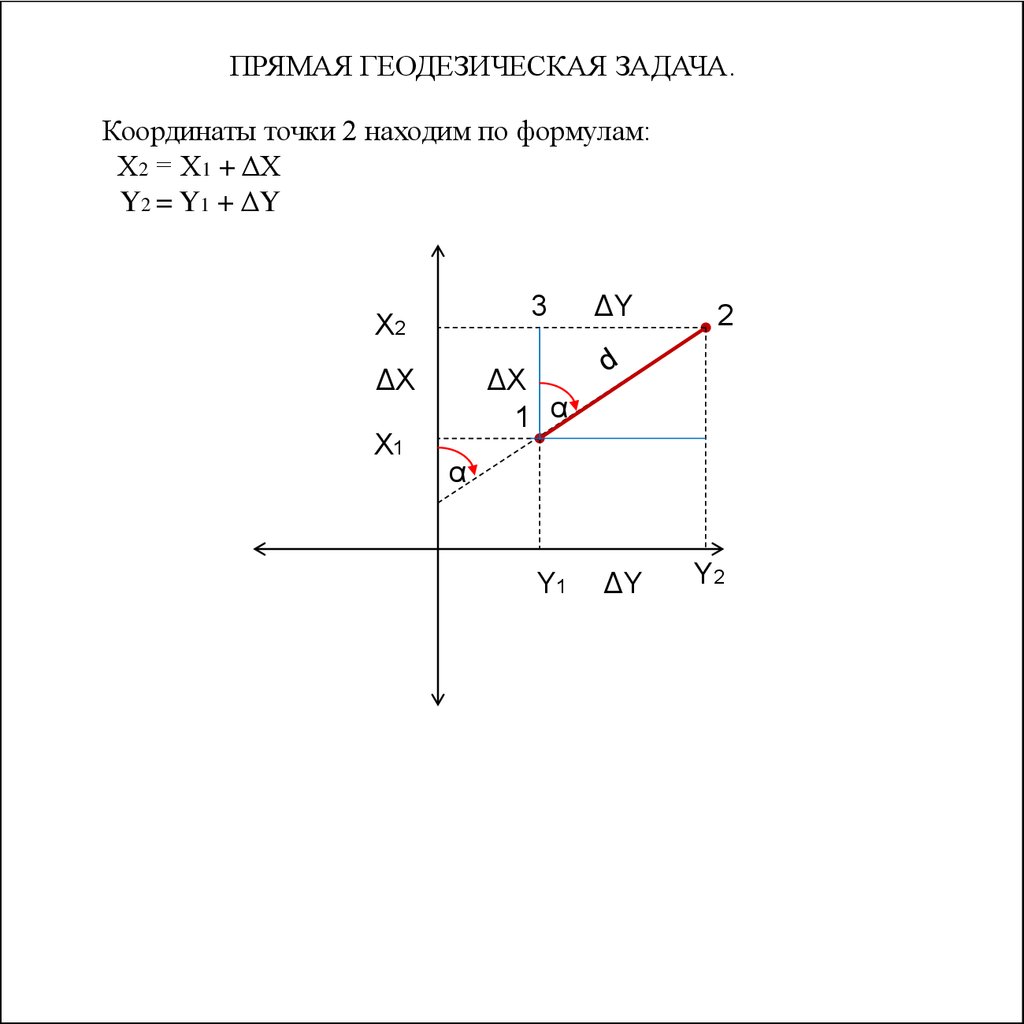
55.
ПРЯМАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧА.Координаты точки 2 находим по формулам:
Х2 = Х1 + ΔХ
Y2 = Y1 + ΔY
3
Х2
ΔХ
X1
ΔY
2
ΔХ
1 α
α
Y1
ΔY
Y2
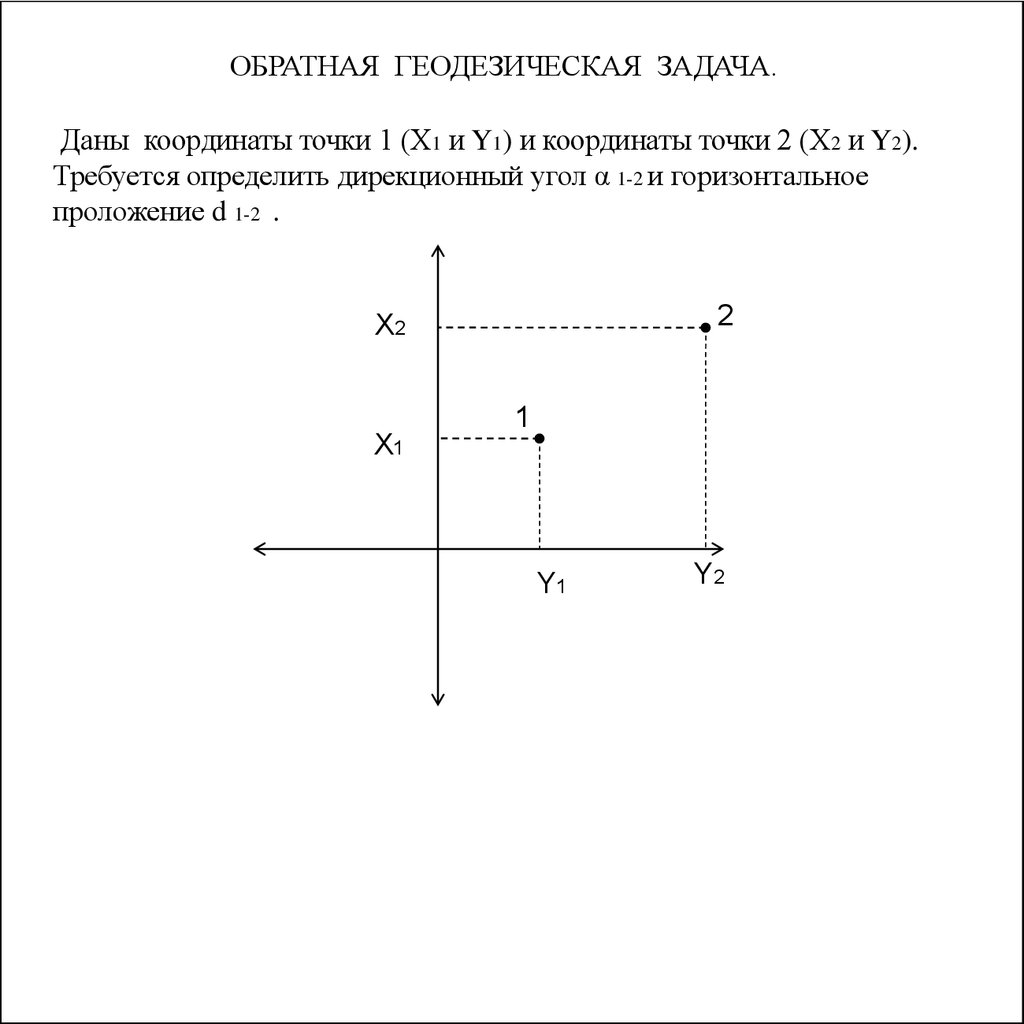
56.
ОБРАТНАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧА.Даны координаты точки 1 (Х1 и Y1) и координаты точки 2 (Х2 и Y2).
Требуется определить дирекционный угол α 1-2 и горизонтальное
проложение d 1-2 .
2
Х2
1
X1
Y1
Y2
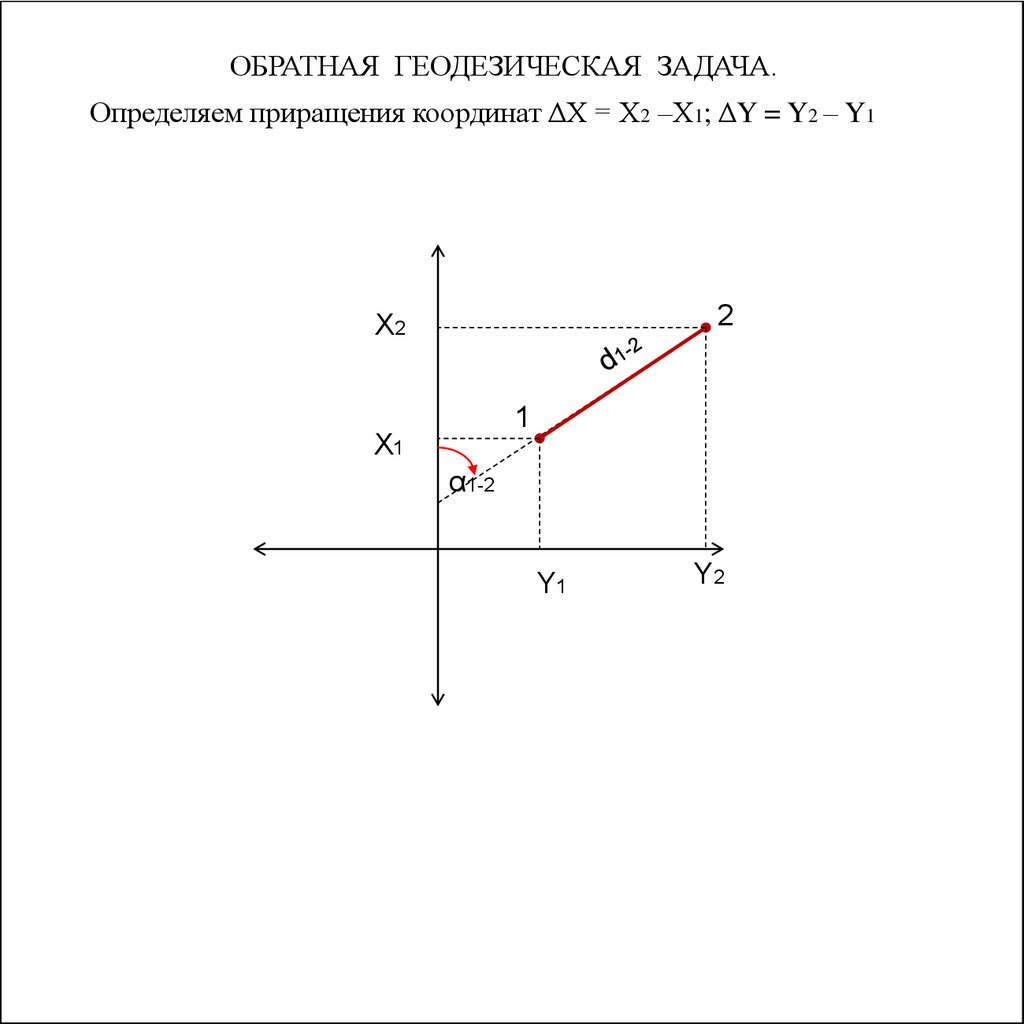
57.
ОБРАТНАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧА.Определяем приращения координат ΔХ = Х2 –Х1; ΔY = Y2 – Y1
2
Х2
1
X1
α1-2
Y1
Y2
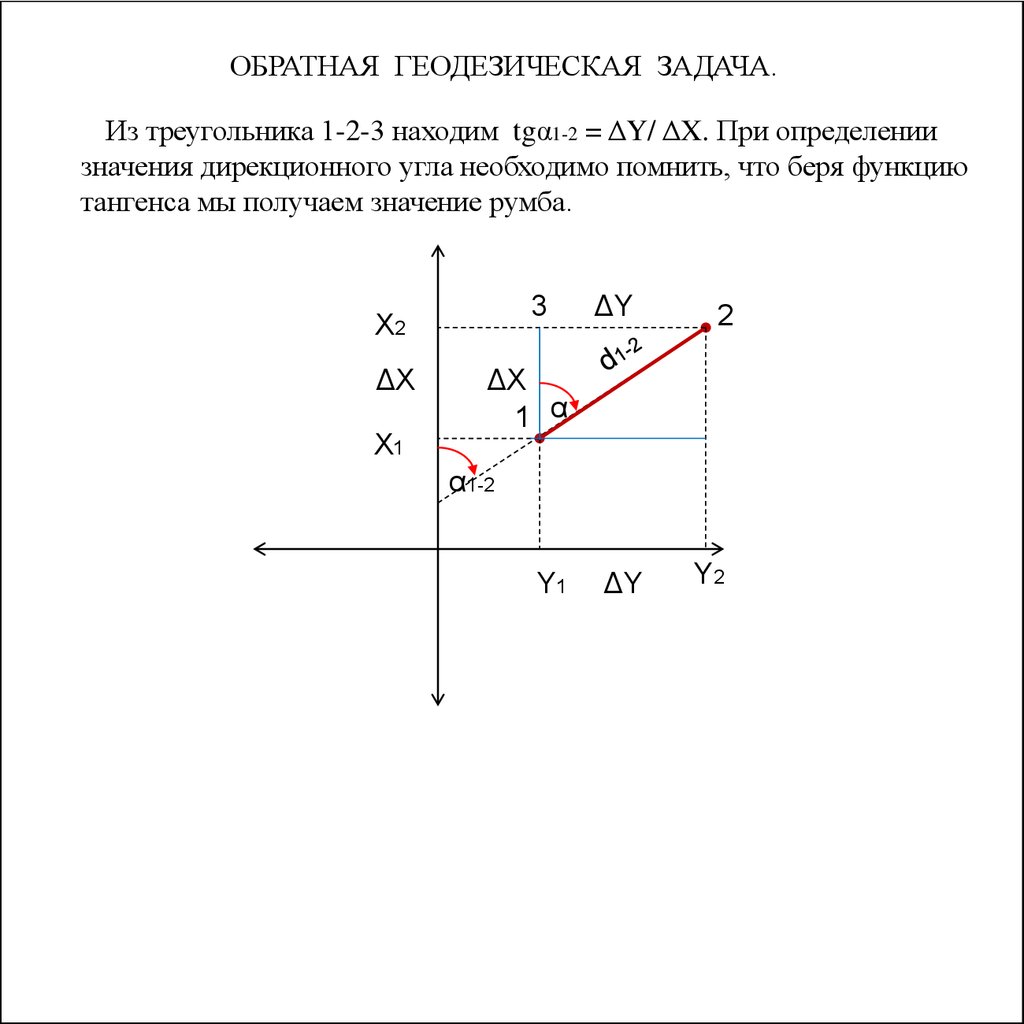
58.
ОБРАТНАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧА.Из треугольника 1-2-3 находим tgα1-2 = ΔY/ ΔX. При определении
значения дирекционного угла необходимо помнить, что беря функцию
тангенса мы получаем значение румба.
3
Х2
ΔХ
ΔY
2
ΔХ
1 α
X1
α1-2
Y1
ΔY
Y2
59.
Для того чтобы определить значение дирекционного угла надо знать знакиприращения координат. Например: ΔX = 58.7 ; ΔY = - 74.2.
tg α = -74.2/ 58.7 = -1.264
r = 51.6523° = 51° 39’14” Знаки приращения координат по четвертям
показаны на рисунке.
+
C
lV + -
l++
В+
- З
lll - -
ll - +
Ю
Таким образом согласно знакам приращений координат наш угол
попадает в lV четверть, т.е. r = СЗ 51°39’14”. Из формул соотношений
дирекционных углов и румбов, определяем, что
α = 360° - r = 360° - 51°39’14” = 308° 20’ 46”
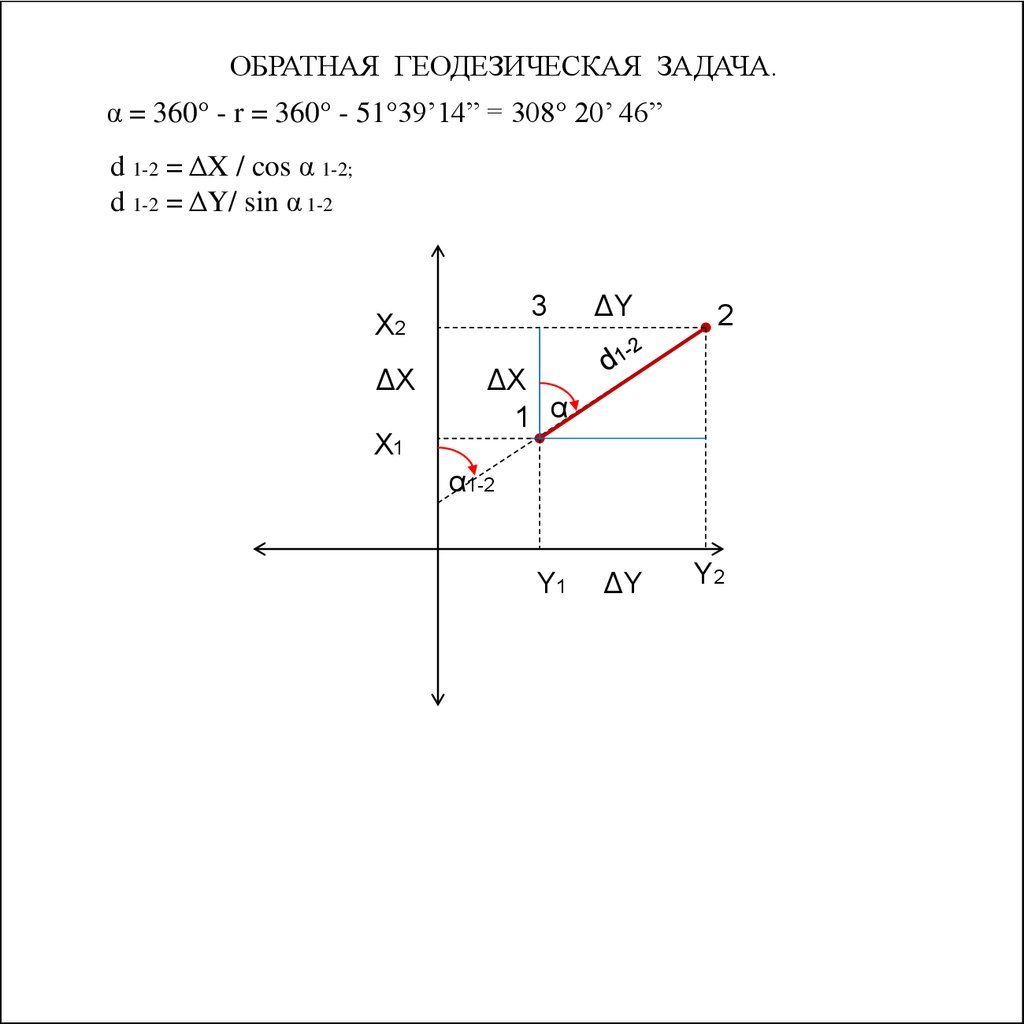
60.
ОБРАТНАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧА.α = 360° - r = 360° - 51°39’14” = 308° 20’ 46”
d 1-2 = ΔX / cos α 1-2;
d 1-2 = ΔY/ sin α 1-2
3
Х2
ΔХ
ΔY
2
ΔХ
1 α
X1
α1-2
Y1
ΔY
Y2
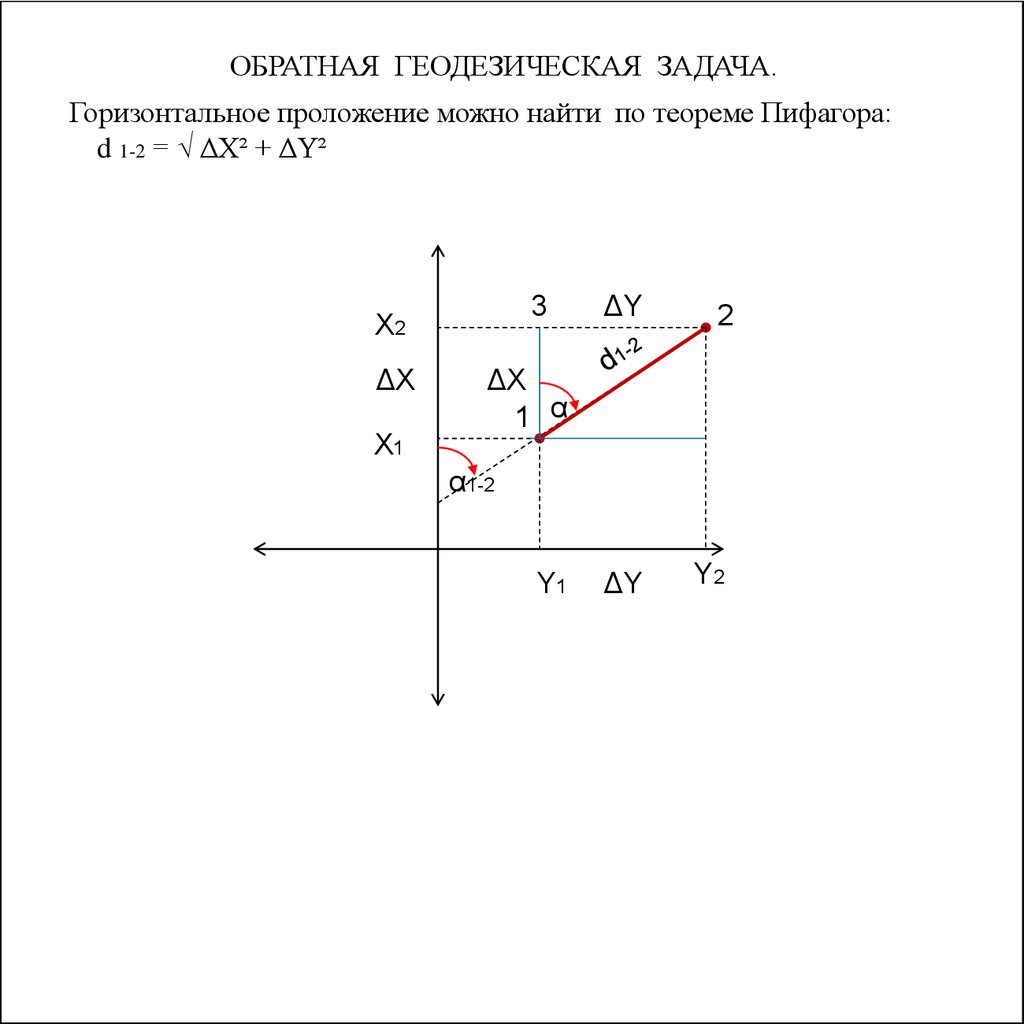
61.
ОБРАТНАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧА.Горизонтальное проложение можно найти по теореме Пифагора:
d 1-2 = √ ΔX² + ΔY²
3
Х2
ΔХ
ΔY
2
ΔХ
1 α
X1
α1-2
Y1
ΔY
Y2
62.
ГОСУДАРСТВЕННАЯ ГЕОДЕЗИЧЕСКАЯ СЕТЬ.Координатная основа Российской Федерации реализована в виде
государственной геодезической сети, закрепляющей систему координат на
территории РФ. Система координат называется геодезической или
референцной. За отсчетную поверхность принят ориентированный в теле
земли эллипсоид Красовского.
Государственная геодезическая сеть включает в себя геодезические
построения различных классов точности:
1. Фундаментальная астрономо-геодезическая сеть (ФАГС)
2. Высокоточная геодезическая сеть (ВГС)
3. Спутниковая геодезическая сеть 1 класса (СГС – 1).
В 2002 году постановлением Правительства РФ на территории России
введена Единая государственная система геодезических координат
1995 года (СК-95).
63.
ПЛАНОВЫЕ И ВЫСОТНЫЕ ГЕОДЕЗИЧЕСКИЕ СЕТИ.Опорным пунктом называется закрепленная на местности точка,
координаты которой известны из геодезических измерений с достаточной
точностью.
Совокупность опорных пунктов равномерно расположенных по всей
территории и служащих основой для съемок, называется опорной сетью.
Различаются плановые геодезические сети , в которых для каждого
пункта определены прямоугольные координаты X, Y в
общегосударственной системе координат, и высотные, в которых высоты
пунктов (Н) определяются в Балтийской системе высот.
Плановые геодезические сети создаются методами триангуляции,
трилатерации и полигонометрии, а также их комбинациями.
64.
Метод триангуляции основан на измерение всех углов треугольника иодной из сторон. Остальные стороны находятся по тригонометрическим
формулам. Измеренная сторона называется базисом. Зная дирекционный
угол α0 базисной стороны b1, а также координаты одной из вершин ХА, YA,
вычисляются координаты всех точек сети.
α0
β1
β2
β4
β3
β5
β6
β7
β8
β9
Метод трилатерации сводится к построению на местности смежных
треугольников и геодезических четырехугольников с измерением в
каждом из них всех сторон и диагоналей. Углы получают путем
тригонометрических вычислений.
65.
В районах где видимость ограничена (например лесной массив) исоздание видимых опорных пунктов связано с большими затратами,
используется метод полигонометрии. Он сводится
к построению на местности ломаной линии
с углами близкими 180 градусов. При применении полигонометрических
сетей замеряют все стороны -d1, d2, d3,…… dn., и углы поворотов
β1, β2,β3…… βn.
А
αAB
С
d1
d2
В
d3
d5
d4
β2
β4
β1
β3
β6
D
β5
По исходным сторонам и углам, имея координату исходной точки А и
дирекционный угол исходного направления АВ вычисляют координаты
вершин полигонов, которые являются опорными пунктами, закрепленные
на местности строительством постоянных сооружений.
66.
Плановая геодезическая сеть делится на четыре класса, где каждыйпоследующий класс опирается на точки более высокого класса.
Государственные геодезические сети 1 класса являются наиболее точными.
Пункты 1 класса располагаются на значительном (20 км. и более)
расстоянии друг от друга. Координаты точек вычисляются от одного начала,
создавая тем самым единую систему координат, которая позволяет
производить геодезические работы на различных участках территории.
На основе пунктов 1 класса развивают последовательно системы
пунктов более низкого класса 2 , 3, 4, вычисляя их координаты от пунктов
более высокого класса.
Помимо геодезических сетей 1-4 класса используются сети сгущения
1 и 2 разрядов, а также геодезические съемочные сети.
Государственные геодезические сети дополняются сетями сгущения 1 и 2
разрядов и съемочными сетями до тех пор, пока их густота не станет
достаточной для съемок ситуации и рельефа местности.
Геодезические сети, используемые для обеспечения топографических
съемок, называются съемочным обоснованием. В это понятие включаются
съемочные сети и сети более высокого порядка, расположенные на участке
съемки.
67.
Государственная нивелирная сеть так же делится на 4 класса. Нивелирнаясеть 1 и 2 класса служит главной высотной основой, посредством которой
устанавливается единая система высот на всей территории страны.
Нивелирование 1 класса выполняется с наивысшей точностью.
Невязки в полигонах или нивелирных ходах последующих классов
допускают не более ±5мм.√L для 2 класса, ± 10мм. √L для 3 класса
и ± 20мм. √L для 4 класса. L – длина нивелирного хода в километрах.
Нивелирные сети 3 и 4 классов служат для развития высотных сетей и
решения инженерных задач.
Высотные сети сгущения создаются методом нивелирования lV класса или
техническим нивелированием. Невязки в ходах и полигонах технического
нивелирования не должны превышать ±50мм. √L.
68.
ЗАКРЕПЛЕНИЕ ПУНКТОВ ГЕОДЕЗИЧЕСКИХ СЕТЕЙ.В городах с многоэтажной застройкой пункты триангуляции
устанавливают на крышах высотных зданий. Такая надстройка
представляет собой столик для прибора в виде кирпичного или
бетонного столба и визирный цилиндр или металлический сигнал,
устанавливаемый над столиком.
Пункты высотной геодезической сети закрепляются специальными
знаками – стенными реперами и марками, грунтовыми реперами.
Отметка стенного репера относится к полочке, на которую
устанавливается рейка при привязке к реперу.
При отсутствии фундаментальных зданий закладываются грунтовые
реперы, в виде отрезка трубы или рейсы заделываемых в бетонные
монолиты. В верхний конец трубы закладывают марки со сферической
головкой. При нивелировании определяют верхнюю точку сферической
головки. Пункты съемочных геодезических сетей закрепляются,
в основном временными знаками: деревянными столбами и кольями,
отрезками металлических труб и т.д. Координаты всех пунктов
плановой геодезической сети, а также отметки пунктов высотной
геодезической сети заносятся в специальные каталоги, в которых
кроме названия пунктов дается описание их месторасположения.
Геодезические пункты, предназначенные для выполнения съемочных
и инженерно – геодезических работ, обычно являются одновременно
пунктами планового и высотного обоснования.
69.
После создания геодезической сети производится съемка подробностейситуации и рельефа. В зависимости от применяемых инструментов и
методов различают несколько видов съемок подробностей.
Теодолитная съемка выполняется теодолитом и мерной лентой.
При этом измеряются только расстояния и горизонтальные углы.
Расстояния можно измерять дальномерами соответствующей точности.
Тахеометрическая съемка сочетает в себе, контурную и вертикальную.
Производится теодолитом, снабженным вертикальным кругом
и дальномером. Превышения измеряются тригонометрическим
нивелированием, путем измерения угла наклона с помощью
вертикального круга. Она позволяет отображать на плане не только
горизонтальную ситуацию, но и рельеф.
Мензульная съемка производится с помощью мензулы и кипрегеля,
инструментов позволяющих непосредственно в поле получать план
местности с изображением рельефа.
Аэрофотосъемка, это съемка специальным фотоаппаратом,
установленном на самолете. Она ведется, в сочетании с геодезическими
работами, необходимыми для привязки снимков к местности, в
плановом и высотном отношениях.
70.
Контрольные вопросы к лекции:1. Что изучает наука геодезия ?
2. Какие проблемы решает инженерная геодезия?
3. Как называется форма земли ?
4. С какой геометрической фигурой сопоставляется форма земли ?
5. Что такое референц эллипсоид ?
6. Какие параметры имеет эллипсоид Красовского ?
7. Назовите существующие системы координат ?
8. Как влияет кривизна земли на точность линейных измерений ?
9. В каких случаях можно применять плоские системы координат ?
10. Как называется проекция применяемая при построении карт ?
В чем ее смысл ?
11. За какую отсчетную отметку в нашей стране принимается нуль
Крондштадского футштока ?
12. Что такое план, карта, профиль ?
13. Чем план отличается от карты ?
14. Что такое масштаб ?
15. Какие виды масштабов вы знаете ? Чем они отличаются ?
16. Что такое точность масштаба ?
17. Дайте определение азимута, дирекционного угла и румба ?
18. Как соотносятся азимуты, магнитные азимуты, дирекционные
углы?
19. Соотношение дирекционных углов и румбов в разных четвертях ?
20. В чем смысл прямой геодезической задачи ?
21. Что определяется при решении обратной геодезической задачи ?
22. Что такое государственная геодезическая сеть ?
71.
23. Что такое опорная геодезическая сеть ?24. Какие методы используются при создании плановых геодезических
сетей ?
25. На сколько классов делятся Государственные геодезические сети ?
26. На сколько классов делятся нивелирные сети ?
27. Для чего создаются сети сгущения и геодезические съемочные сети ?
28. Как закрепляются пункты геодезической сети ?
29 Как закрепляются пункты нивелирной сети ?
30. Перечислите виды геодезических съемок ?















































 География
География








