Комбинаторные задачи на нахождение числа перестановок из n элементов, сочетаний и размещений из n элементов по k (k ≤ n)

1. Комбинаторные задачи на нахождение числа перестановок из n элементов, сочетаний и размещений из n элементов по k (k ≤ n)

Урок №8
КОМБИНАТОРНЫЕ ЗАДАЧИ НА
НАХОЖДЕНИЕ ЧИСЛА
ПЕРЕСТАНОВОК ИЗ
N ЭЛЕМЕНТОВ,
СОЧЕТАНИЙ
И РАЗМЕЩЕНИЙ
ИЗ N ЭЛЕМЕНТОВ
ПО K (K ≤ N)
МБОУ СОШ № 167 г.НОВОСИБИРСКА
УЧИТЕЛЬ МАТЕМАТИКИ
ВАСИЛЕВА МАРИНА ЮРЬЕВНА

2. Цель:

ЦЕЛЬ:
продолжить формирование умений
находить число перестановок,
сочетаний и размещений из п
элементов по k.

3. Проверочная работа.

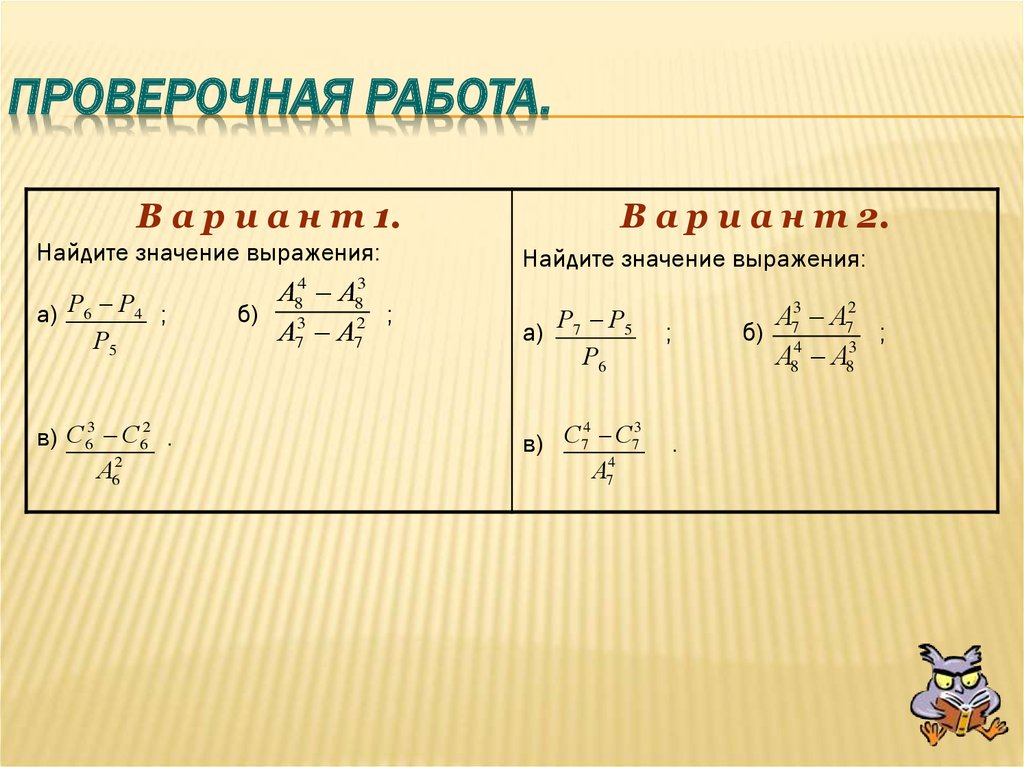
ПРОВЕРОЧНАЯ РАБОТА.
В а р и а н т 1.
Найдите значение выражения:
а) Р6 Р4 ;
Р5
3
2
в) С6 С6 .
А62
б)
А А
А А
4
8
3
7
3
8
2
7
В а р и а н т 2.
Найдите значение выражения:
;
а) Р7 Р5
Р6
4
3
С
С
7
7
в)
А74
;
.
А73 А72
б) 4
;
3
А8 А8

4. Формирование умений и навыков.

ФОРМИРОВАНИЕ УМЕНИЙ И
НАВЫКОВ.
Свойства сочетания из п элементов по k (п ≥ k)
Cnk Cnn k
П р и м е р:
– первое свойство;
C62 C64.
Cnk 11 Cnk 1 Cnk , k n
П р и м е р:
– второе свойство;
C128 C118 С. 117
Решаем задачи с применением формул нахождения числа
перестановок, сочетаний и размещений.
№ 776
№ 777
№ 778
(а; в)
№ 779
№ 780
№ 782

5. Домашнее задание: 778(б), № 781, № 844, № 855*(а, в).

ДОМАШНЕЕ
ЗАДАНИЕ: 778(Б), №
781, № 844,
№ 855*(А, В).

6.

№ 776
Решение
а) Фиксируем один элемент «в». Количество
перестановок из пяти оставшихся элементов:
Р5 = 5! = 1 · 2 · 3 · 4 · 5 = 120.
б) Фиксируем два элемента «а» и «т».
Количество перестановок из 4 оставшихся
элементов:
Р4 = 4! = 1 · 2 · 3 · 4 = 24.
О т в е т: а) 120 анаграмм; б) 24 анаграммы.

7.

№ 777
Решение
Мальчики и девочки должны чередоваться, то есть девочки
могут сидеть только на четных местах, а мальчики только на
нечетных. Поэтому девочки могут меняться местами только с
девочками, а мальчики – только с мальчиками. Четырех
девочек можно рассадить: Р4 = 4! = 24 способами, а пятерых
мальчиков Р5 = 5! = 120 способами.
Каждый способ размещения девочек может сочетаться с
каждым способом размещения мальчиков, поэтому по правилу
произведения общее число способов равно: Р4 · Р5 = 24 · 120 =
2880.
О т в е т: 2880 способов.

8.

№ 778
(а; в)
Решение
Выбираем три элемента из 12, порядок выбора не имеет
значения (все трое идут в наряд).
а) Иванов и Петров идут в наряд, еще одного нужно выбрать
из других 10 солдат; количество способов выбора:
= 10.
1
в) ИвановСидет
в наряд, а Петров остается. Еще двоих, идущих
10
в наряд с Ивановым, нужно выбрать из других 10 солдат
(Иванова и Петрова не считаем); количество способов:
.
10! 9 · 10в) 45 способов.
2 способов;
О т в е т: а) С
10
45
10
2!8!
1·2

9.

№ 779
Решение
а) Выбираем 4 шахматистов из 16 без указания
порядка; количество способов:
16! 13 · 14 · 15 · 16
4
С16
1820 .
4!12!
1 ·2 ·3 ·4
б) Выбираем 4 шахматистов из 16 с указанием
порядка их расположения в команде; количество
способов:
16!
4
= 13 · 14 · 15 · 16 = 43680.
А
16
12!
О т в е т: а) 1820 способов;
б) 43680 способов.

10.

№ 780
Решение
Выбираем (без повторений) 2 буквы из 5 и 3 цифры из 10;
порядок выбора учитывается (например: 213 кт и 321 тк –
разные).
Количество способов выбора А52 5! 4 · 5 = 20 (для букв);
(для цифр).3!
5!
4 · 5 = 20
Каждый 3!
вариант выбора букв может сочетаться с каждым
А52
вариантом выбора цифр, поэтому, по комбинаторному правилу
умножения, общее число способов равно:
2
3
А
·
А
20
·
720
14400
5
10
О т в е т: 14400 способов.

11.

№ 782
Решение
Выбираем из группы туристов в п человек четырех дежурных
(порядок выбора значения не имеет); число способов . Затем
4
выбираемСиз
группы туристов в п человек двух дежурных – число
п
4
способов . Так как число способов выбораСчетырех
дежурных в
п
13 раз больше, чем двух, получаем уравнение:
= 13 ·
;
;
п!
13 · п!
2
;
Сп4
Сп
4!( п 4)!
2!( п 2)!
;
п!
13 · п!
1
13
2! · 3 · 4 · (п 4)!
2!( п 4)!( п 3) ( п 2)
12
( п 3) ( п 2)
п2 – 5п – 150 = 0;
п1 = 15, п2 = –10. Так как п N, то п2 = –10 – не удовлетворяет
условию, значит, п = 15.
О т в е т: 15 туристов.

12.

ПРИ ПОДГОТОВКЕ ПРЕЗЕНТАЦИЙ ИСПОЛЬЗОВАНЫ
МАТЕРИАЛЫ :
•Алгебра. 9 класс: поурочные планы по учебнику Ю. Н.
Макарычева (компакт-диск) – издательство «Учитель», 2010
•Алгебра: для 9 класса общеобразовательных учереждений/
Ю. Н.Макарычев, Н.Г. Миндюк, К.И. Нешков, С. Б. Суворова;
под редакцией С.А. Телековского.-М.: Просвещение, 2009.
•http://ux1.eiu.edu/~jbarford/WiseOwl.jp
•http://www.prazdnik.by/upload/iblock/1ba/1bada0379d7ea1bb7c894d429
7ec6f76.jpg
•http://smile.zerk.ru/big-yellow/