Похожие презентации:
Симплекс-метод
1. Симплекс-метод
Лекции 6, 72. Симплекс-метод с естественным базисом
Симплекс –метод основан напереходе от одного опорного плана к
другому, при котором значение целевой
функции возрастает при условии, что
задача имеет оптимальный план и
каждый опорный план является
невырожденным.
Этот переход возможен, если
известен какой-либо опорный план.
3.
В этом случае каноническая задачалинейного программирования должна
содержать единичную подматрицу
порядка m
Тогда очевиден первоначальный
опорный план( неотрицательное
базисное решение системы
ограничений КЗЛП).
4.
Рассмотрим задачу, для которой это возможно.Пусть требуется найти максимальное значение
функции
F = c1 x1 + c2 x2 + ... + cn xn
при условиях
ì x1 + a1m +1 xm +1 + ... + a1n xn = b1 ,
ï x + a x + ... + a x = b ,
ï 2 2 m +1 m +1
2n n
2
í
ï.............................................,
ïî xm + amm +1 xm +1 + ... + amn xn = bm ,
x j ³ 0, ( j = 1, n).
aij , bi , c j (i = 1, m, j = 1, n)
m < -заданные
n, bi > 0.
Здесь
постоянные числа, причем
5.
Перепишем ЗЛП в векторнойформе: найти максимум
n
функции
F = åcjxj
j =1
при условиях
Здесь
x1 P1 + x2 P2 + ... + xn Pn = P0 ,
x j ³ 0 ( j = 1, n).
æ b1 ö
æ1ö
æ0ö
ç ÷
ç ÷
ç ÷
b
0
1÷
2 ÷
ç
ç
÷
ç
P0 =
; P1 =
; P2 =
;...;
ç ... ÷
ç ... ÷
ç ... ÷
ç ÷
ç ÷
ç ÷
è0ø
è0ø
è bm ø
æ a1m +1 ö
æ a1n ö
æ0ö
ç
÷
ç
÷
ç ÷
a
a
0
Pm = ç ÷ ; Pm +1 = ç 2 m +1 ÷ ; Pn = ç 2 n ÷ .
ç ... ÷
ç ... ÷
ç ... ÷
ç
÷
ç
÷
ç ÷
a
a
è1ø
è mm +1 ø
è mn ø
6.
Так как b1 P1 + b2 P2 + ... + bm Pm = P0,
то по определению опорного плана
X = (b1 , b2 ,..., bm , 0, 0,..., 0)
,
где последние компоненты вектора
равны нулю, является опорным планом
Опорный план называется
невырожденным, если он содержит m
положительных компонент. В противном
случае он называется вырожденным.
7.
План, при котором целевая функцияЗЛП принимает свое максимальное
(минимальное ) значение , называется
оптимальным
Этот план определяется системой
единичных векторов , которые образуют
базис m-векторного пространства.
Проверка на оптимальность
опорного плана происходит с помощью
критерия оптимальности.
8. Признак оптимальности.
1)Опорный план ЗЛП являетсяоптимальным, если
m
D j = z j - c j = å ci aij - c j ³ 0
i =1
для любого
j = 1, n
.
9.
2)Если для некоторого j=k D k < 0и среди чисел aik (i = 1, m)
нет положительных, т.е. aik £ 0 , то
целевая функция ЗЛП не ограничена на
множестве ее планов, т.е. ЗЛП не имеет
решения, так как нет конечного
оптимума.
10.
3)Если же для некоторого kвыполняется условие D k < 0 , но среди
чисел aik есть положительные, т.е. не
все aik £ 0, то можно получить новый
опорный план, для которого значения
целевой функции
F ( X ¢) > F ( X ) .
На основании признака оптимальности
делаем вывод о целесообразности
перехода к новому опорному плану.
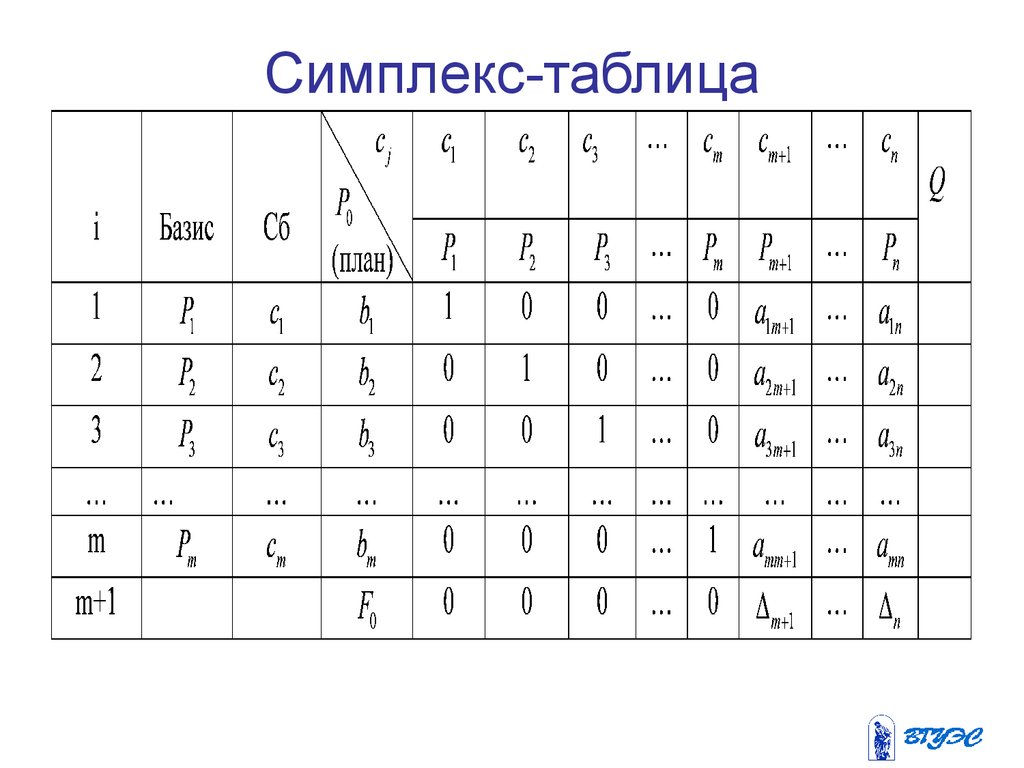
11. Симплекс-таблица
12. Симплекс-таблица
В столбце Сб записывают коэффициенты принеизвестных целевой функции, имеющие те же
индексы, что и векторы данного базиса.
В столбце P0 -положительные компоненты исходного
опорного плана, в нем же в результате вычислений
получают положительные компоненты оптимального
плана.
Первые m строк заполняют по исходным данным
задачи, а показатели (m+1)-й строки вычисляют. В
этой строке в столбце вектора P0 записывают
значение целевой функции, которое она принимает
при данном опорном плане, а в столбце вектора Pj значение D j = z j - c j .
13.
Здесьz = cá × Pj
, т.е.
m
z j = å ci aij = c1a1 j + c2 a2 j + ... + cm amj ( j = 1, n)
i =1
Значение
F0 = P0 × cá = c1b1 + c2b2 + ... + cmbm .
После заполнения таблицы исходный
опорный план проверяют на оптимальность.
Для этого просматривают элементы (m+1)-й
строки. Может иметь место один из 3-х
случаев.
14.
1) Все D j ³ 0. Тогда составленныйплан оптимален.
2) D j < 0 для некоторого j и все
соответствующие этому j aij £ 0 . Тогда
целевая функция неограничена.
3) D j < 0 для некоторых индексов j и
для каждого такого j по крайней мере
одно из чисел aij положительно.
Здесь можно перейти к новому
опорному плану.
15.
Этот переход осуществляетсяисключением из базиса какого-нибудь
из векторов и включением в него
другого.
В базис вводим вектор , давший
минимальную отрицательную величину
симплекс-разности
D k = min( z j - c j ),
( j = 1, n)
16.
Из базиса выводится вектор Pr ,который дает наименьшее
положительное оценочное отношение
bi
Q = min( )
aik
для всех aik > 0 , т.е. минимум
достигается при i=r.
Число ark называется разрешающим
элементом.
17.
bibr
Q = min( ) =
, aik > 0, i = 1, m.
aik
ark
Строка Pr называется разрешающей
строкой, элементы этой строки в новой
симплекс-таблице вычисляются по
методу Жордана-Гаусса, т.е. по
формулам:
arj¢ =
arj
ark
, j = 1, n, i = r.
18.
Элементы i-й строки –по формуламaij¢ = aij -
arj aik
ark
, i = 1, m, j = 1, n.
19.
Значение нового опорного планасчитают по формулам
br
br¢ =
äëÿ i = r , i = 1, m;
ark
br aik
bi¢ = bi äëÿ i ¹ r , i = 1, m.
ark
Значение целевой функции при
переходе от одного опорного плана к
другому , улучшенному, изменяется по
¢
F
= F - D k Q.
формуле
20.
Процесс решения продолжаем дополучения оптимального плана либо до
установления неограниченности ЦФ.
Если среди оценок оптимального плана
нулевые только оценки , соответствующие
базисным векторам, то оптимальный план
единствен.
Если же нулевая оценка соответствует
вектору, не входящему в базис, то в общем
случае это означает, что опорный план не
единствен.
21. Алгоритм применения симплекс-метода
Алгоритм применения симплексметода1)Находят опорный план.
2)Составляют симплекс-таблицу.
3)Выясняют, имеется ли хотя бы одна
отрицательная оценка. Если нет, то
найденный опорный план оптимален.
Если же есть отрицательные оценки, то
либо устанавливают неразрешимость
задачи, либо переходят к новому
опорному плану.
22.
4)Находят направляющие столбец истроку. Направляющий столбец
определяется наибольшим по
абсолютной величине отрицательным
числом D j , а направляющая строка—
минимальным числом Q.
5)Определяют положительные
компоненты нового опорного плана.
Составляется новая таблица.
6)Проверяют найденный опорный план
на оптимальность.
23. Пример.
Решить симплекс-методом ЗЛПF = 10 x1 + 20 x2 ® max
ì x1 + 3,5 x2 £ 350,
ï
í2 x1 + 0,5 x2 £ 240,
ï x + x £ 150,
î 1 2
x1,2 ³ 0.
24. Решение.
Приведем задачу к каноническому виду, введяx3 , x4 , x5.
новые переменные
В целевую функцию эти переменные войдут с
нулевыми коэффициентами:
F = 10 x1 + 20 x2 + 0 x3 + 0 x4 + 0 x5 ® max,
ì x1 + 3,5 x2 + x3 = 350,
ï
í2 x1 + 0,5 x2 + x4 = 240,
ï x + x + x = 150,
î 1 2 5
x1,2,3,4,5 ³ 0.
25.
Из коэффициентов при неизвестных исвободных членов составим векторы
æ1ö
æ 3,5 ö
æ1ö
æ0ö
æ0ö
æ 350 ö
ç ÷
ç ÷
ç ÷
ç ÷
ç ÷
ç
÷
P1 = ç 2 ÷ , P2 = ç 0,5 ÷ , P3 = ç 0 ÷ , P4 = ç 1 ÷ , P5 = ç 0 ÷ , P0 = ç 240 ÷
ç1÷
ç 1 ÷
ç 0÷
ç0÷
ç1÷
ç 150 ÷
è ø
è ø
è ø
è ø
è ø
è
ø
Единичные векторы образуют единичную
подматрицу и составляют базис
первоначального плана. Свободные
неизвестные приравниваются к нулю.
Получаем первоначальный опорный план:
Х= (0;0;350;240;150).
26.
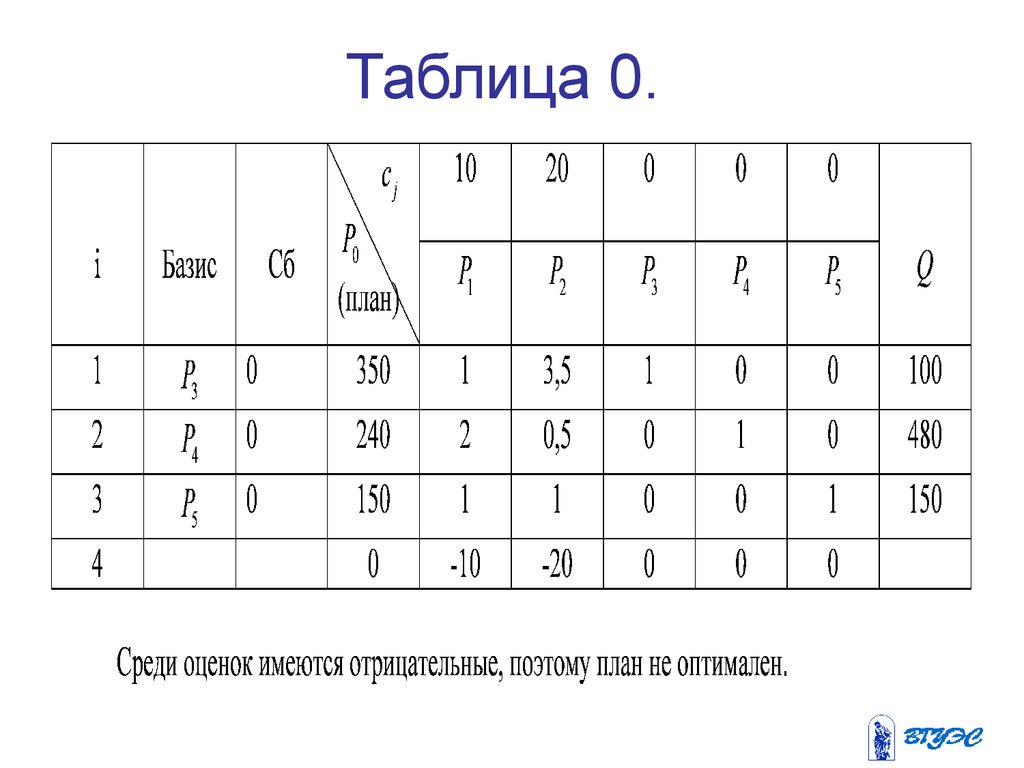
Составим симплекс-таблицу и проверим планна оптимальность. В нашем примере
m = 3, n = 5.
Для заполнения последней строки таблицы
сразу вычислим симплекс-разности
m
D j = z j - c j = å ci aij - c j :
i =1
Для этого поочередно умножаем столбец Сб
на соответствующие элементы каждого
столбца P1 , P2 , ...
27.
D1 = z1 - c1 = 0 ×1 + 0 × 2 + 0 ×1 - 10 = -10,D 2 = z2 - c2 = 0 × 3,5 + 0 × 0,5 + 0 ×1 - 20 = -20,
D 3 = z3 - c3 = 0 ×1 + 0 × 0 + 0 × 0 - 0 = 0,
D 4 = z4 - c4 = 0 ×1 + 0 × 0 + 0 × 0 - 0 = 0,
D 5 = z5 - c5. = 0 × 0 + 0 × 0 + 0 ×1 - 0 = 0.
Составим теперь нулевую симплексную
таблицу
28. Таблица 0.
29.
Определяем разрешающий элементсимплексной таблицы. Т.к. имеется 2
отрицательные оценки, то выбираем ту, что
дает максимальную по абсолютной величине
отрицательную оценку, т. е. -20.
Это означает, что в базис включается
вектор P2 , а исключается из базиса тот
вектор, которому соответствует
ì bi ü br
Q = min í ý =
i
î aik þ ark
(aik > 0, i = 1, m)
.
30.
ì bi üì 350 240 150 ü
Q = min í ý = min í
,
, ý = min { 100, 480,150} =
i
î 3,5 0,5 1 þ
î aik þ
br b1
=
=
= 100.
ark a12
Разрешающим элементом
является a12 = 3,5 .
Значение целевой функции в
следующей симплекс-таблице будет
равно:(1)
(0)
(0) (0)
F ( X ) = F ( X ) - D k Q = 0 - (-20) ×100 = 2000
31.
Элементы направляющей строки вновой таблице вычисляем, деля эту
строку на ведущий элемент(в том числе
и клетку в столбце план):
(0)
11
a
a
1
=
=
= 0, 286,
a12 3,5
a12(1)
a12(0) 3,5
1
(1)
=
=
= 1, a13 =
= 0, 286,
a12 3,5
3,5
(1)
11
(1)
14
a
0
0
(1)
=
= 0, a15 =
= 0.
3,5
3,5
32.
Можно рассчитывать элементы строкметодом Жордана-Гаусса, домножая 1ю строку на (-0,5) и прибавляя ее ко 2-й,
а затем на(-1) и прибавляя к 3-й,
обнулив таким образом элементы 2-го
выделенного (разрешающего) столбца,
или по формулам треугольника
ari aik
a = aij ark
'
ij
br aik
b = bi , i ¹ r.
ark
'
i
33.
Элементы 2-ой строки получаем пометоду Жордана-Гаусса (или по
формулам треугольника)
(1)
21
a11
1 × 0,5
= a21 = 2= 1,857,
a12
3,5
(1)
22
a12 a22
3,5 × 0,5
= a22 = 0,5 = 0,
a12
3,5
a
a
(1)
23
a
= a23 -
.......
a13 a 22
a12
1 × 3,5
= 0= -0,143,
3,5
34.
Аналогично рассчитываем элементы 3й строки.Значения нового опорного плана
рассчитываем по формулам:
(1)
2
b1a22
350 × 0,5
= b2 = 240 = 190,
a12
3,5
(1)
3
b1a22
350 ×1
= b3 = 150 = 50.
a12
3,5
b
b
После чего заполняем таблицу 1.
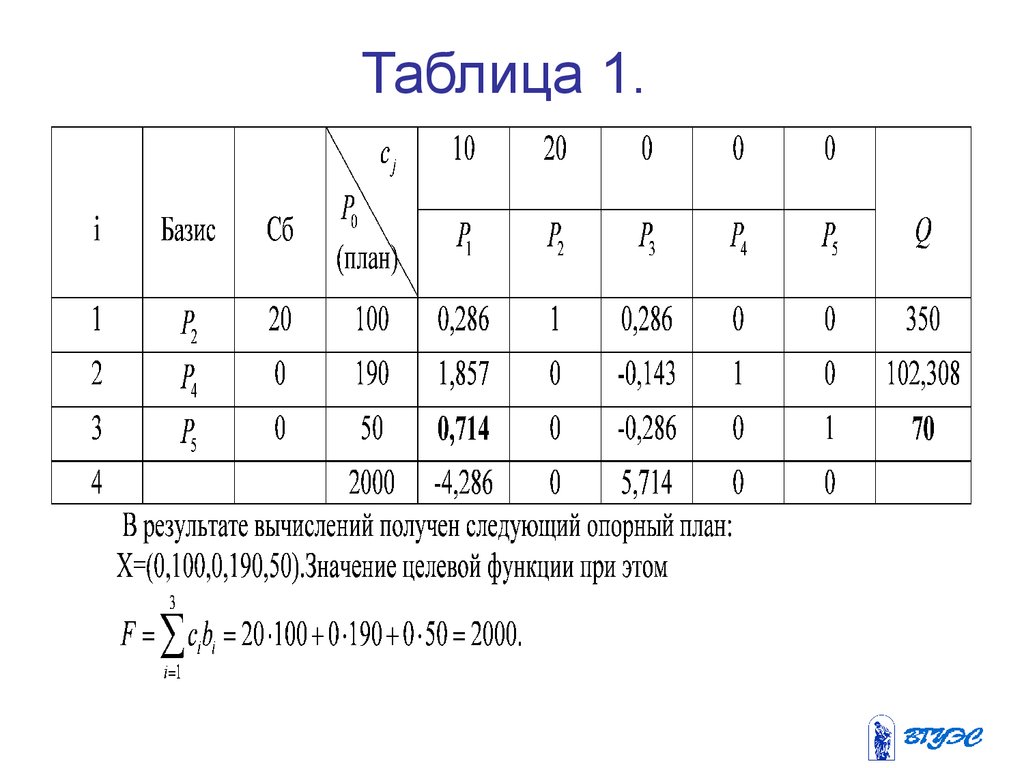
35. Таблица 1.
36.
Проверим план на оптимальность.Вычислим симплекс-разности.
D1(1) = z1 - c1 = 20 × 0, 286 + 0 ×1,857 + 0 × 0, 714 - 10 = -4, 286,
D (1)
2 = z2 - c2 = 20 × 1 + 0 × 0 + 0 × 0 - 20 = 0,
D 3(1) = z3 - c3 = 20 × 0, 286 + 0 × (-0,143) + 0 × (-0, 286) -0 = 5, 714,
D (1)
4 = z4 - c4 = 20 × 0 + 0 × 1 + 0 × 0 - 0 = 0,
D 5(1) = z5 - c5 = 20 × 0 + 0 × 0 + 0 ×1 - 0 = 0.
37.
В первом столбце матрицы имеетсяотрицательная оценка. План не
оптимален, но его можно улучшить ,
включив в базис вектор P1 . Найдем
минимальное оценочное отношение:
ì bi ü
50 ü
ì 100 190
Q = min í ý = min í
;
;
ý=
î 0, 286 1,857 0, 714 þ
î aik þ
b3
= min { 350;102,308;70} =
= 70.
a31
38.
Выводится из базиса вектор P5 , которомусоответствует минимальное оценочное
отношение 70. Переходим к следующему
опорному плану. Вводим в базис вектор P1 ,
делим разрешающую строку на
разрешающий элемент a31 = 0, 714 и
заполняем 3-ю строку таблицы 2. После чего
методом Жордана-Гаусса домножаем эту
строку на (-0,286) и прибавляем к первой,
затем домножим эту строку на (-1,857) и
прибавляем ко второй.
39. Таблица 2
40.
Вычисляем симплекс-разности.D1 = z1 - c1 = 20 × 0 + 0 × 0 + 10 ×1 - 10 = 0,
D 2 = z2 - c2 = 20 ×1 + 0 × 0 + 10 × 0 - 20 = 0,
D 3 = z3 - c3 = 20 × 0, 4 + 0 × 0, 6 + 10 × (-0, 4) - 0 = 4,
D 4 = z4 - c4 = 20 × 0 + 0 ×1 + 10 × 0 - 0 = 0,
D 5 = z5 - c5 = 20 × (-0, 4) + 0 × (-2, 6) + 10 ×1, 4 - 0 = 6.
План оптимален. Значение целевой
функции
F = 10 × 70 + 20 × 80 + 0 × 60 = 2300.





































 Математика
Математика Программирование
Программирование








