Тепломассообмен. Конвекция и теплопроводность

1.

Тепломассообмен.
Конвекция и
теплопроводность

2.

Лекции 1,2

3.

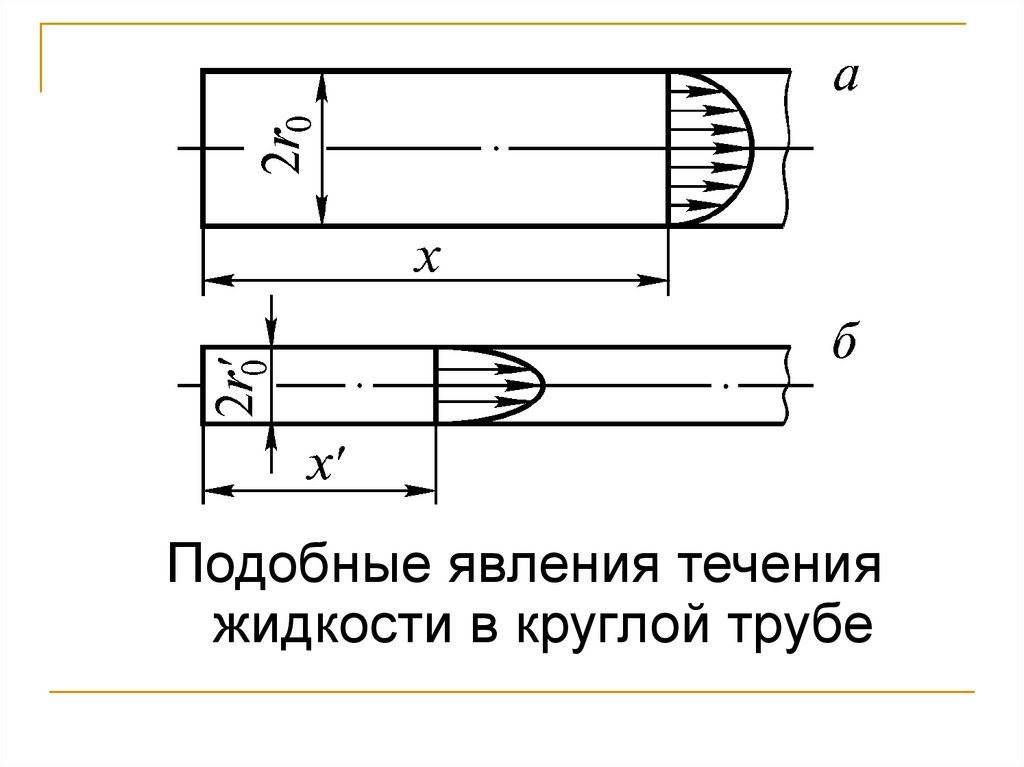
Подобные явления течения
жидкости в круглой трубе

4.

Уравнение для первого потока в трубе:
Уравнение для второго потока в трубе:
Так как:
После подстановки получим:

5.

Разделив обе части уравнения на
- число гомохронности
- число Фруда
- число Эйлера
- число Рейнольдса
:

6.

Физический смысл критериев подобия
0 (fин) =
u2
0/l
Еu = 0 (fдавл)/0 (fин)
0 (fгр) = g
Fr = 0 (fин)/0 (fгр)
0 (fтр) = νu0/l2
Re = 0 (fин)/0(fтр)

7.

Связь между критериями подобия
Уравнения Навье-Стокса:
Где:
?

8.

Уравнения Навье-Стокса в другом виде:
Умножим уравнение (1) и (2) на:
Умножим уравнение (3) на:

9.

После преобразований получим:
Где:
То есть:

10.

Лекции 3-5

11.

Основные понятия тепло- и масообмена
T T ( x, y , z , t )
q qx i q y j qz k
Сi Ci ( x, y, z, t )
m m x i m y j mz k

12.

Постулат Фурье
где λ – коэффициент теплопроводности, Вт/(м*К),
T – абсолютная температура, К
Если ввести обозначение a=λ/(ρ*cp), постулат Фурье примет вид:
где i – объемная энтальпия, Дж/м3;
a – коэффициент температуропроводности, м2/с.
i c pT

13.

Постулат Фика
где Di – коэффициент диффузии, м2/с;
ρi – парциальная плотность i компонента смеси, кг/м3
Если ρi=ρCi, то постулат Фика имеет вид:
где Сi – массовая доля i компонента смеси;
ρ – плотность смеси, кг/м3.

14.

Тройная аналогия

15.

Плотность теплового потока за счет конвективного переноса:
где ρ – плотность газа, кг/м3;
w – вектор скорости, м/с;
сP – удельная теплоемкость, Дж/(кг*К);
T – абсолютная температура, К
Плотность теплового потока за счет молекулярного переноса
(постулат Фурье):
Суммарная плотность теплового потока:

16.

Плотность потока массы примеси за счет конвективного переноса:
где ρ – плотность смеси, кг/м3;
w – вектор скорости, м/с;
Сi – доля i компонента в смеси
Плотность потока массы за счет молекулярного переноса
(постулат Фика):
Суммарная плотность потока массы:

17.

Формула Ньютона для конвективной теплоотдачи:
где α – коэффициент теплоотдачи, Вт/(м2К);
T0 – температура жидкости, К;
Tw – температура поверхности, К
Формула для конвективной массоотдачи:
где β – коэффициент теплоотдачи, м/с;
ρi0 – парциальная плотность i примеси в жидкости, кг/м3;
ρiw – парциальная плотность i примеси на стенке, кг/м3

18.

Формулы для конвективной теплоотдачи и массоотдачи могут быть
в записаны следующем виде:
где α – коэффициент теплоотдачи, Вт/(м2К);
ΔT – температурный напор, К;
β – коэффициент теплоотдачи, м/с;
Сi0 – доля i компонента в жидкости;
Сiw – доля i компонента смеси на стенке

19.

Поток тепла за счет теплоотдачи:
Если qw=const:
Поток массы примеси за счет массоотдачи:
Если mw=const:

20.

Лекции 6-8

21.

Уравнения конвективной тепло- и массотдачи
Перенос тепла через бесконечно тонкий слой:
Перенос тепла за счет теплоотдачи:
На основании закона сохранения энергии получим:
- Уравнение конвективной
теплоотдачи

22.

Перенос массы примеси через бесконечно тонкий слой:
Ci
miw Di
n n 0
Перенос массы примеси за счет масоотдачи:
miw Сi
На основании закона сохранения массы:
- Уравнение конвективной
массоотдачи

23.

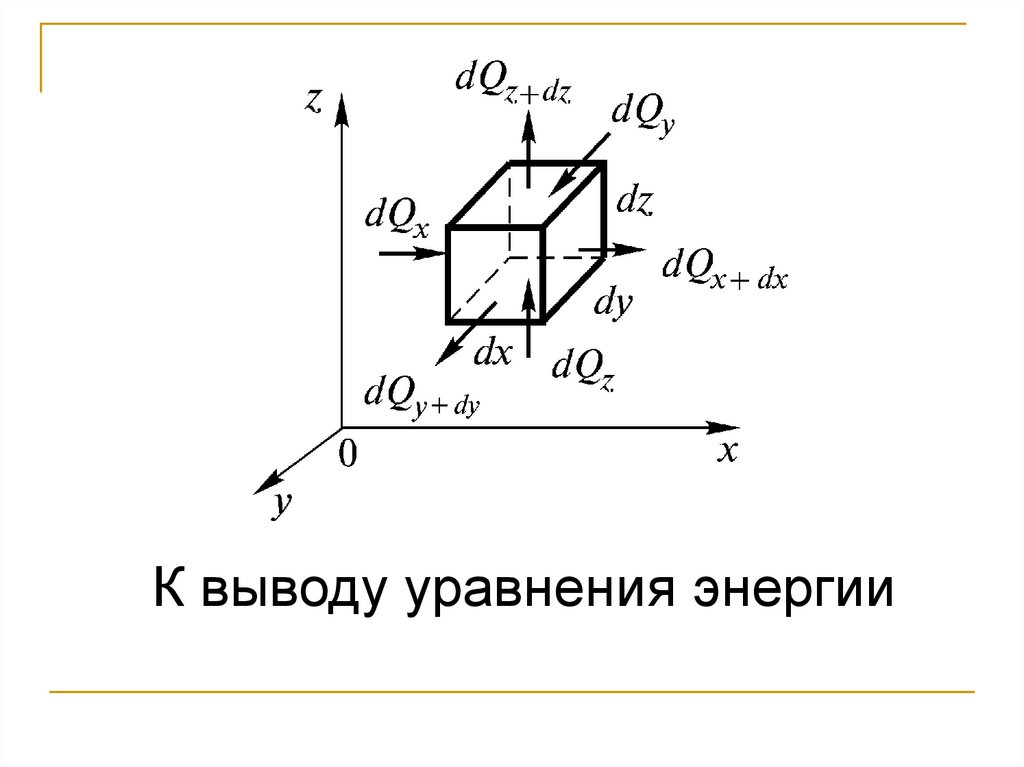
К выводу уравнения энергии

24.

dQx = qx dydzdt
dQx+dx = qх+dxdydzdt = qx + ∂qx/∂xdx
Аналогично для осей y и z:
d2Qz = dQz – dQz+dz = = –(дqz/дz) dVdt
Или:

25.

С другой стороны:
На основании закона сохранения энергии:
Учитывая, что
Или разделив на ρcp и расписав div:
Где:
получим:

26.

Учитывая, что divw=0 для несжимаемой жидкости и a=λ/ρcP получим:
Или:
dT
- Полная (субстанциальная производная)
dt
- Уравнение энергии для
несжимаемой жидкости

27.

Аналогичным образом выводится уравнение конвективной
диффузии:
Или:
С другой стороны:
На основании закона сохранения массы и подставляя выражения
для плотности потока массы примеси после преобразований
получим:

28.

Или:
dС
- Полная (субстанциальная производная)
dt
- Уравнение конвективной диффузии

29.

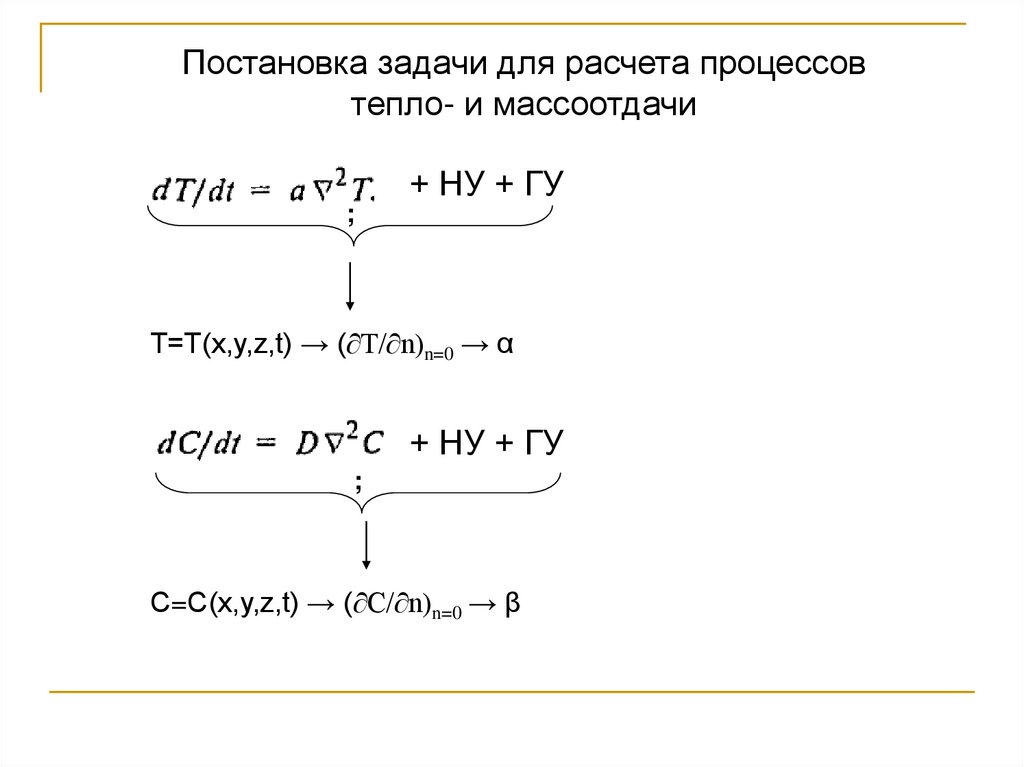
Постановка задачи для расчета процессов
тепло- и массоотдачи
+ НУ + ГУ
;
T=T(x,y,z,t) → (∂T/∂n)n=0 → α
+ НУ + ГУ
;
С=С(x,y,z,t) → (∂С/∂n)n=0 → β

30.

Лекции 9-14

31.

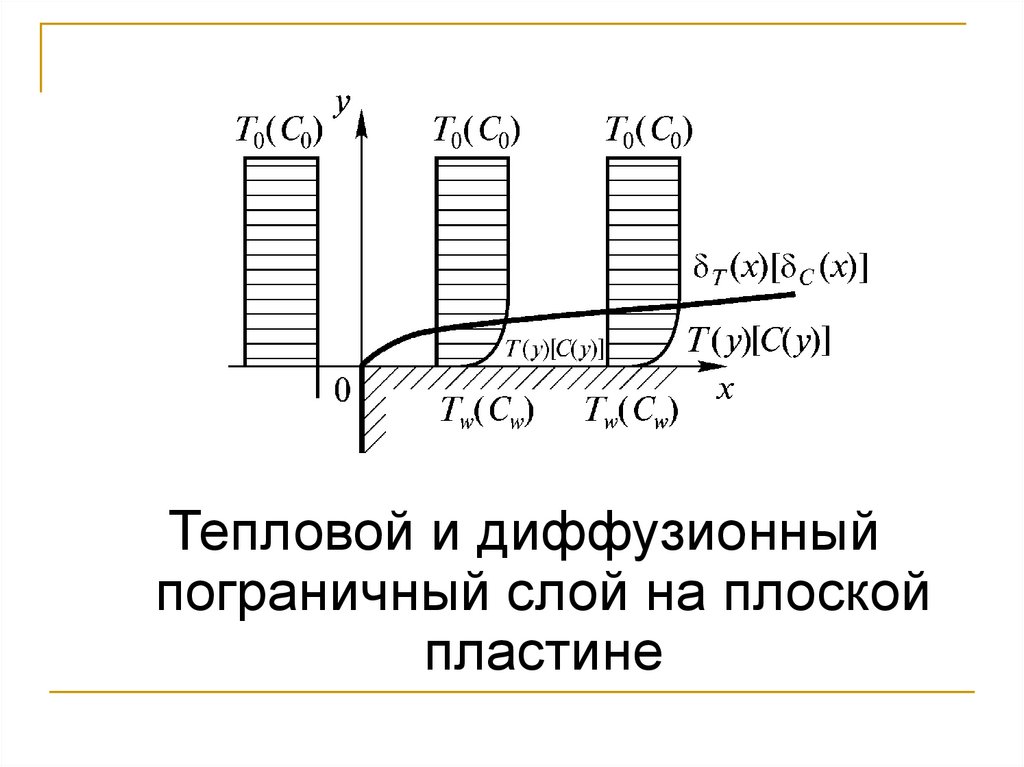
Тепловой и диффузионный
пограничный слой на плоской
пластине

32.

?
Т
?
С
δ = δ(ν); δТ = δТ(a); δC = δC(Di)
f ;
f
Т
a C
Di
Pr ;
a
Sc
Di
- критерий Прандтля
- критерий Шмидта

33.

Уравнение энергии для описания стационарного течения
несжимаемой жидкости имеет вид:
Оценим порядки всех входящих в него величин:
- Уравнение Польгаузена
Или учитывая, что
:

34.

Анализ интенсивностей молекулярного и
конвективного механизмов переноса
тепла
Плотность теплового потока за счет конвективного механизма в
направлении X:
uсPT ; O( uсPT ) 1
Плотность теплового потока за счет конвективного механизма в
направлении Y:
vсPT ; O( vсPT )
Плотность теплового потока за счет молекулярного механизма в
направлении X:
T
T
; O (
) 2
x
x
Плотность потока импульса за счет молекулярного механизма в
направлении Y:
T
T
; O (
)
y
y

35.

Уравнение ковективной диффузии для описания стационарного
течения несжимаемой жидкости имеет вид:
Оценивая порядки всех входящих в него величин получим:
- Уравнение конвективной диффузии
для турбулентного пограничного слоя
Или учитывая, что
:

36.

Анализ интенсивностей молекулярного и
конвективного механизмов переноса
массы примеси
Плотность потока массы примеси за счет конвективного
механизма в направлении X:
uСi ; O( uСi ) 1
Плотность потока массы примеси за счет конвективного
механизма в направлении Y:
vCi ; O( vCi )
Плотность потока массы примеси за счет молекулярного
механизма в направлении X:
Di
Ci
C
; O( Di i ) 2
x
x
Плотность потока массы примеси за счет молекулярного
механизма в направлении Y:
C
C
Di i ; O( Di i )
y
y

37.

Граничные условия для уравнения Польгаузена:
Граничные условия для уравнения конвективной диффузии:

38.

Уравнение энергии для турбулентного
пограничного слоя
Так как:
Получим:
- Уравнение энергии для
турбулентного пограничного
слоя;
- плотность турбулентного теплового потока, Вт/м2

39.

Уравнение конвективной диффузии для
турбулентного пограничного слоя
Так как:
Получим:
- Уравнение конвективной
диффузии для
турбулентного пограничного
слоя;
- плотность турбулентного теплового потока, Вт/м2

40.

Граничные условия:
Неизвестные величины:
T T ( x, y )
?
qТ qТ ( x, y )
Сi Сi ( x, y)
?
mТ mТ ( x, y)
Таким образом, система уравнения являются незамкнутыми

41.

К полуэмпирической теории
Прандтля для переноса тепла и
массы примеси

42.

Закон сохранения энергии для турбулентного моля при
переходе из 1-1 в 2-2:
Если ρ=const и cP=const:
Разложим среднюю скорость в ряд Тейлора:

43.

Учитывая то, что:
Тогда для плотности турбулентного теплового потока получим:
Для пристеночного пограничного слоя :
где k – эмпирическая константа.
Для свободного пограничного слоя :
lu k x
где k – эмпирическая константа.

44.

Аналогичным образом для плотности турбулентного потока
массы примеси:
Или переписывая уравнения для плотности теплового потока
и плотности потока массы примесив другом виде:
– коэффициент турбулентной
температуропроводсти
– коэффициент турбулентной
диффузии

45.

Турбулентное число Прандтля:
Турбулентное число Шмидта:
Значения чисел Прандтля и Шмидта:
ScТ 0,75

46.

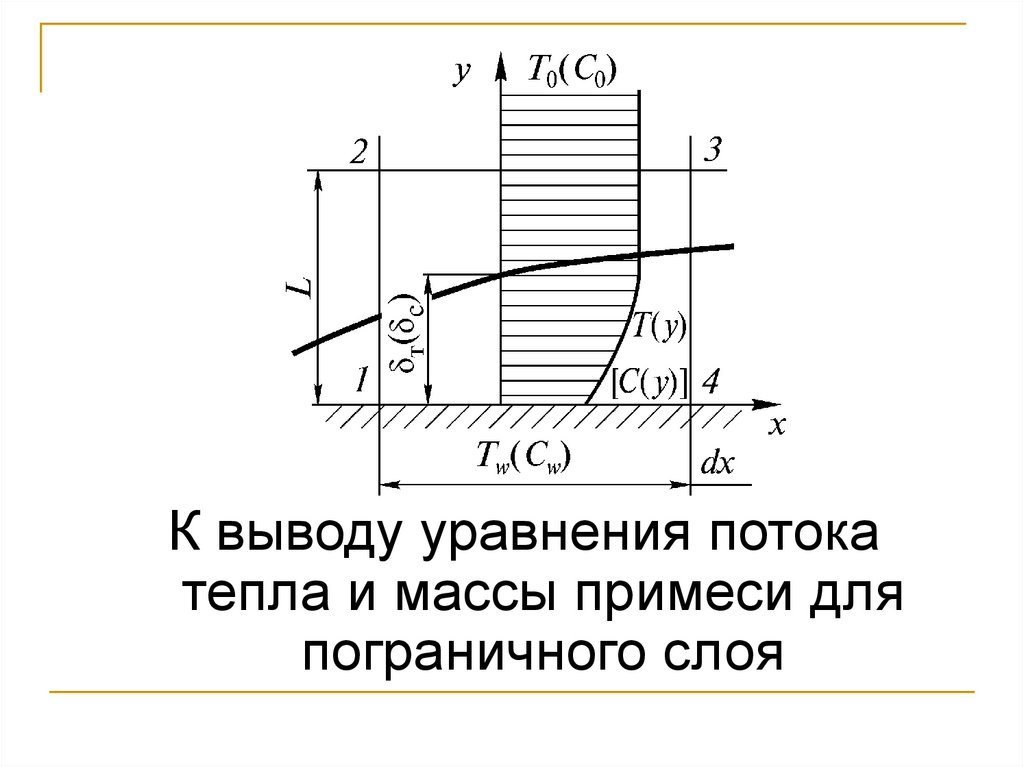
К выводу уравнения потока
тепла и массы примеси для
пограничного слоя

47.

Закон сохранения энергии:
Найдем поток тепла в плоскости 1-2:
Найдем поток тепла в плоскости 3-4:
Поток тепла в плоскости 2-3:

48.

Масса, проходящая через плоскость 2-3:
Тогда поток тепла в плоскости 2-3 окончательно:
Поток тепла в плоскости 1-4:

49.

Имеем:
После сокращений получаем:
Поскольку ρ=const, сP=const и при δ < y < L u=T0:
- Уравнения Кружилина для
пограничного слоя
на плоской пластине

50.

Для ламинарного пограничного слоя уравнение Кружилина
имеет вид:
Для турбулентного пограничного слоя уравнение Кружилина
записывается следующим образом:
qw
d
(T0 T )u dy
dx 0
cP

51.

Аналогичным образом запишем закон сохранения массы
примеси:

52.

После простых преобразований получим:
Для ламинарного пограничного уравнение имеет вид:
Для турбулентного пограничного слоя уравнение
записывается следующим образом:
mwi
d
(С0 С )u dy
dx 0

53.

Лекции 15-18

54.

Теплоотдача при вынужденном
ламинарном движении жидкости вдоль
плоской пластины
Цель: найти T(x,y) , δT(x), α(x)
Распределение u(y) найдено ранее:
Введем избыточную температуру:
Тогда:

55.

Уравнение Кружилина для потока тепла в терминах избыточной
температуры:
Найдем избыточную температуру с помощью аппроксимации:
Для нахождения неизвестных коэффициентов запишем
граничные условия:

56.

Тогда:
Найдем профиль избыточной температуры:

57.

Подставляя полученные результаты в исходное уравнение и
производя интегрирование получим:
Для решения уравнения введем искомую функцию:
Тогда уравнение примет вид:
Разделим на ε (ε=0 – частное решение):

58.

После интегрирования получим:
Но при этом:
что лишено физического смысла
Значит ε=0

59.

Поскольку
где
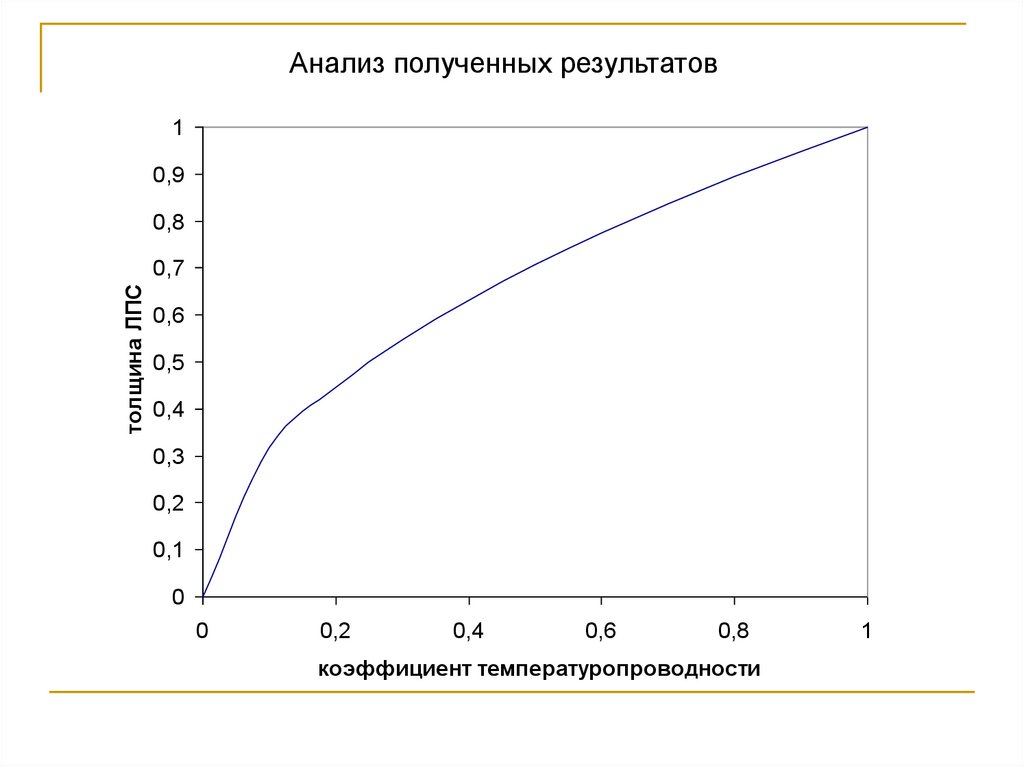
1) δт ~ x0,5
2) δт ~ a0,5
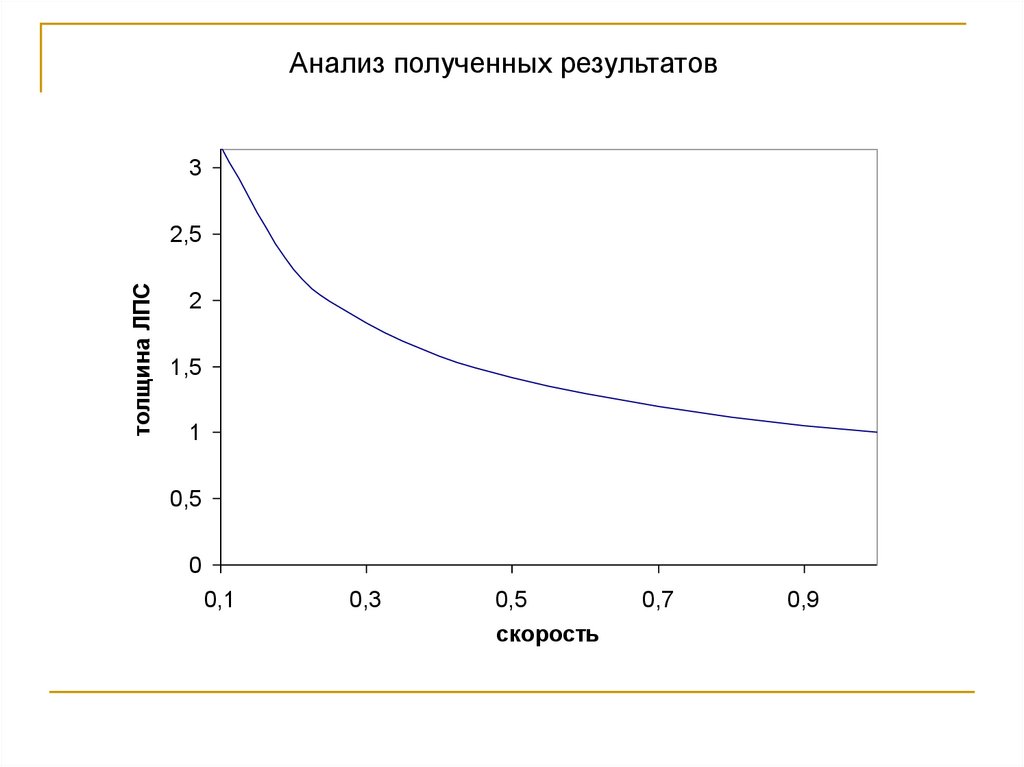
3) δт ~ u0-0,5
:

60.

Анализ полученных результатов
толщина теплового ЛПС
1
0,9
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0
0
0,2
0,4
0,6
Х
0,8
1

61.

Анализ полученных результатов
1
0,9
0,8
толщина ЛПС
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0
0
0,2
0,4
0,6
0,8
коэффициент температуропроводности
1

62.

Анализ полученных результатов
3
толщина ЛПС
2,5
2
1,5
1
0,5
0
0,1
0,3
0,5
скорость
0,7
0,9

63.

Найдем коэффициент теплоотдачи:
Или подставляя :
1) α ~
x-0,5
x Т (
u
) y 0
y
2) α ~
a2/3
a (
u
) y 0 , но интенс.
y
3) α ~ u0
0,5
u
u0 ( ) y 0
y

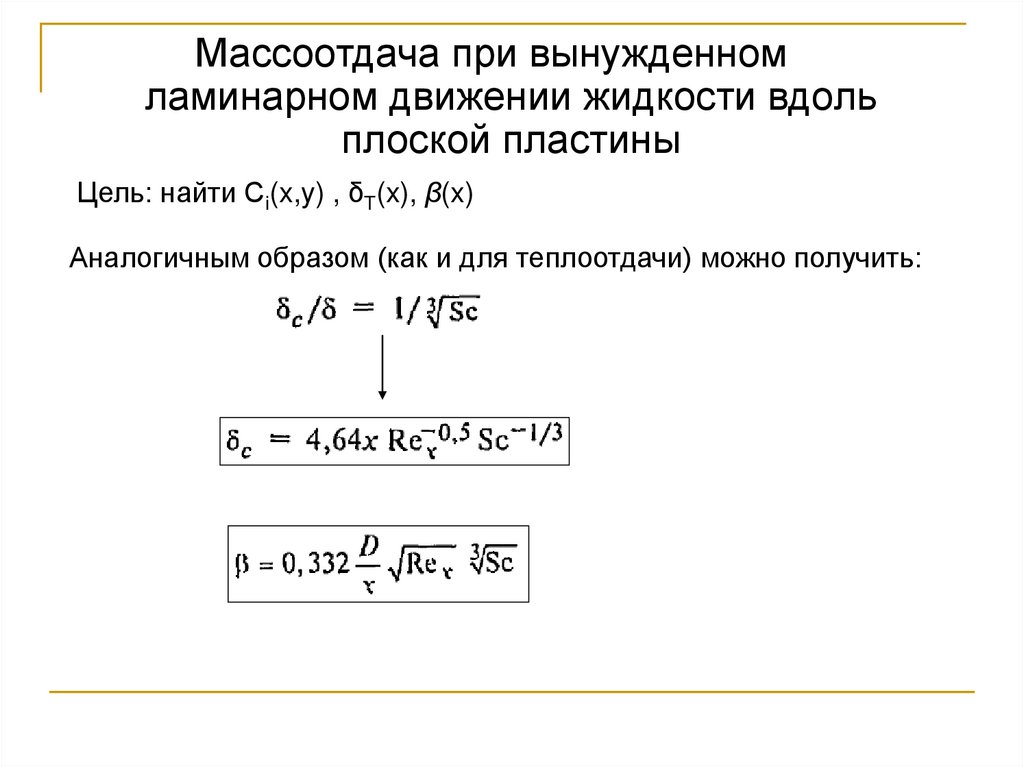
64.

Массоотдача при вынужденном
ламинарном движении жидкости вдоль
плоской пластины
Цель: найти Сi(x,y) , δT(x), β(x)
Аналогичным образом (как и для теплоотдачи) можно получить:

65.

Числа Нуссельта и Шервуда
- Безразмерный коэффициент
теплоотдачи (число Нуссельта)
- Безразмерный коэффициент
массоотдачи (число Шервуда)
С учетом полученных выше соотношений:

66.

Средний по длине пластины коэффициент теплоотдачи:
Аналогично средний коэффициент массоотачи:

67.

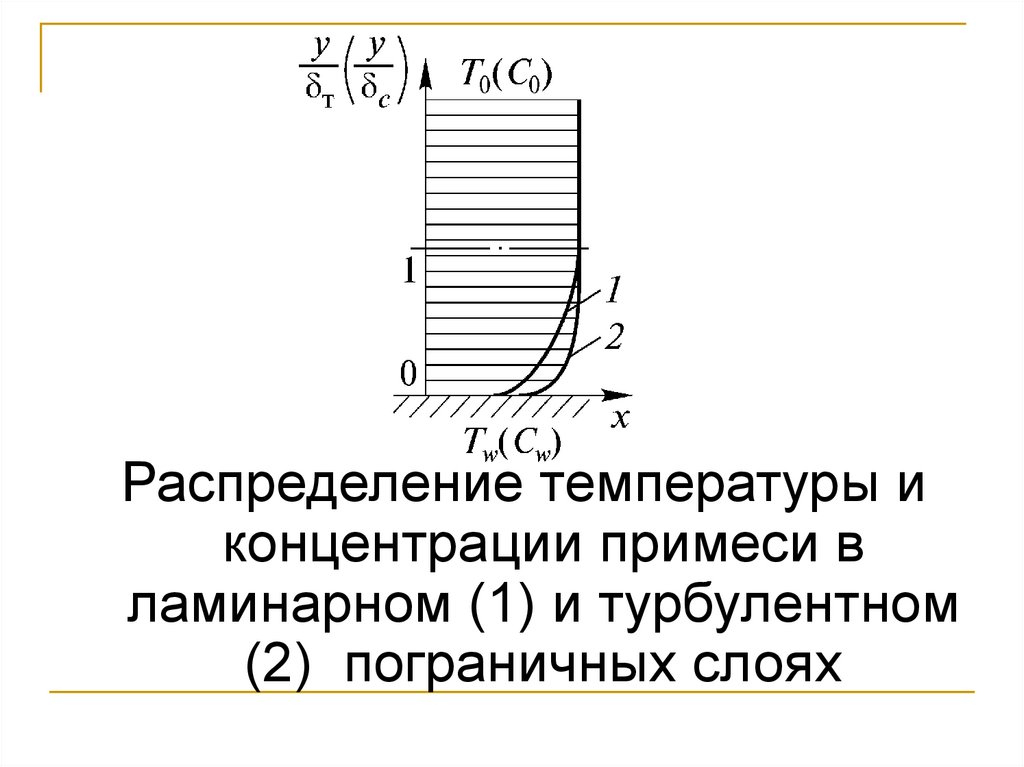
Распределение температуры и
концентрации примеси в
ламинарном (1) и турбулентном
(2) пограничных слоях

68.

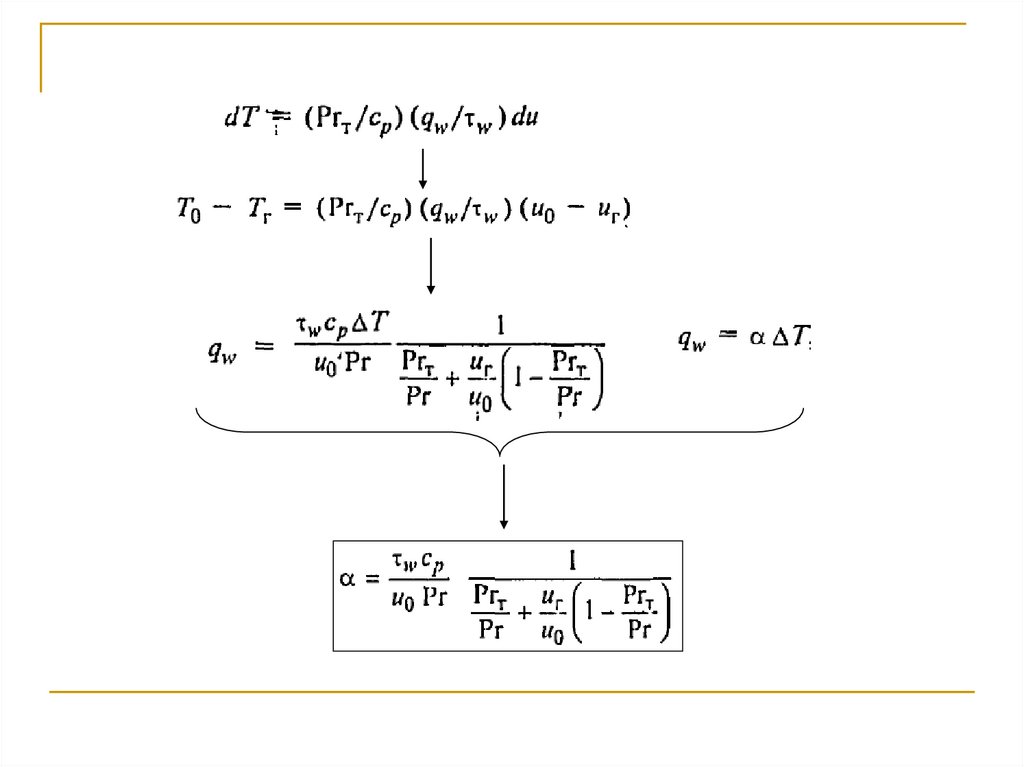
Рассмотрим для турбулентной зоны. Предположим, что:

69.

70.

Для газов:
Аналогичным образом для коэффициента массотдачи можно
получить:
Или для газов:

71.

Анализ полученных результатов
1) α ~ x-0,2 (для ЛПС α ~ x-0,5)
2) α ~ an (для ЛПС α ~ ν2/3)
3) α ~ u00,8 (для ЛПС α ~ u00,5)
1) β ~ x-0,2 (для ЛПС β ~ x-0,5)
2) β ~ Di n (для ЛПС β ~ ν0,5)
3) β ~ u00,8 (для ЛПС β ~ u00,5)

72.

Средний по длине пластины коэффициент теплоотдачи:
Средний по длине пластины коэффициент массоотдачи:

73.

Теплоотдача при установившемся
движении жидкости в трубе
а) При ламинарном режиме при qw=const
Для течения Пуазейля в трубе было плучено:
Уравнение энергии:

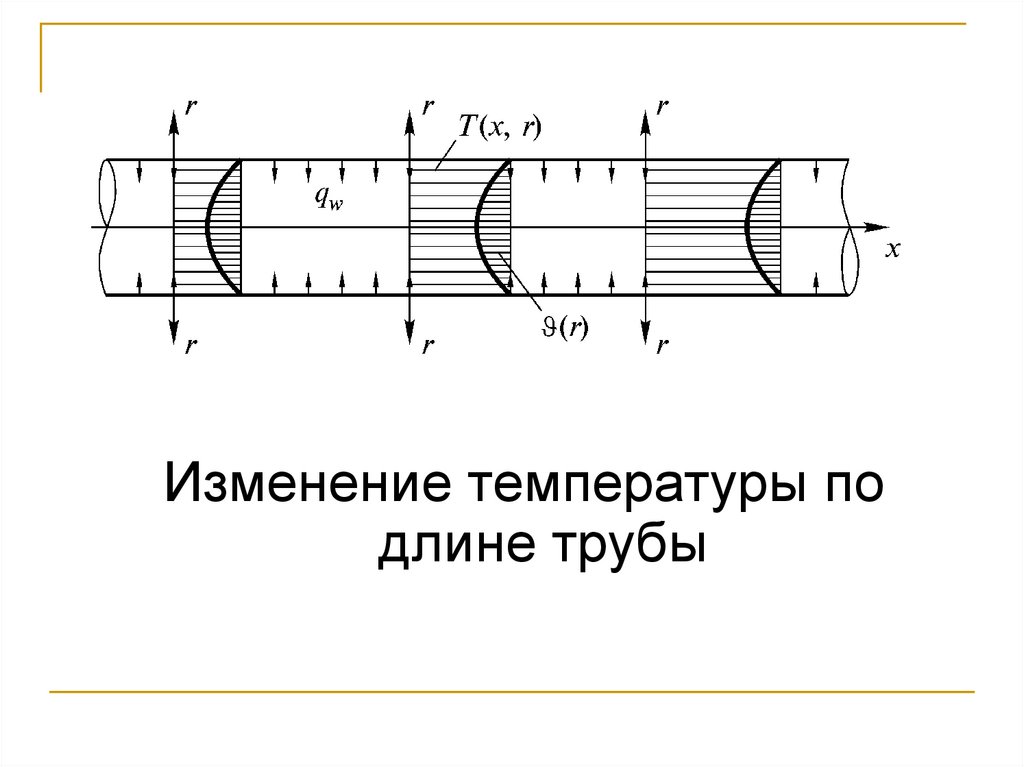
74.

Изменение температуры по
длине трубы

75.

Введем дефект температуры:
Тогда:
Введем безразмерный дефект температуры:
Тогда:

76.

Учтем граничные условия:
Тогда:
С учетом того, что средний дефект температур θ=1:

77.

Анализ полученных результатов
1) α ≠ f(x)
2) α ~ d-1
3) α ≠ f(u)
4) α ~ λ

78.

б) При турбулентном режиме при qw=const
В режиме гидравлически гладкой трубы
Тогда:
Или в безразмерном виде:

79.

Анализ полученных результатов
1) α ≠ f(x)
2) α ~ d-0,2 (при ламинарном режиме α ~ d-1)
3) α = u0,8 (при ламинарном режиме α ≠ f(u)
4) α ~ an (при ламинарном режиме α ~ a)

80.

Лекции 19,20

81.

Пограничный слой при
естественной конвекции

82.

Закон Архимеда для объема жидкости:
Порядок массовой плотности силы Архимеда:
Порядок массовой плотности силы инерции:
Порядок массовой плотности силы внутреннего трения:

83.

Критерий Архимеда:
Введем понятие термического коэффициента расширения:
Т.к. удельный объем обратно пропорционален плотности:
Подставляя в формулу Архимеда:
- Критерий Грасгофа

84.

Таким образом для свободной конвекции:

85.

Лекция 21

86.

Применение теории подобия для
исследования процессов тепло- и
массоотдачи
Уравнение энергии:
Уравнение теплоотдачи:
Граничные условия:

87.

Коэффициент теплоотдачи:
Введем избыточную температуру:
Тогда:
Граничные условия:

88.

Введем безразмерные величины:
Тогда:

89.

Таким образом:
Средний коэффициент теплоотдачи:
Аналогично для среднего коэффициента массоотдачи:

90.

Лекция 22

91.

- стационарная теплопроводность
- нестационарная теплопроводность
Цель:
-?
-?

92.

Уравнение теплопроводности:
Если λ=const и qV=0 уравнение теплопроводности имеет вид:
Или в цилиндрических координатах:
В осесимметричных задачах:

93.

Виды граничных условий
а) граничные условия первого рода:
б) граничные условия второго рода:
в) граничные условия третьего рода:

94.

Лекции 23-26

95.

Уравнение теплопроводности в стационарном режиме:
1) Стационарное температурное поле в плоской стенке
Постоянные интегрирования зависят от граничных условий

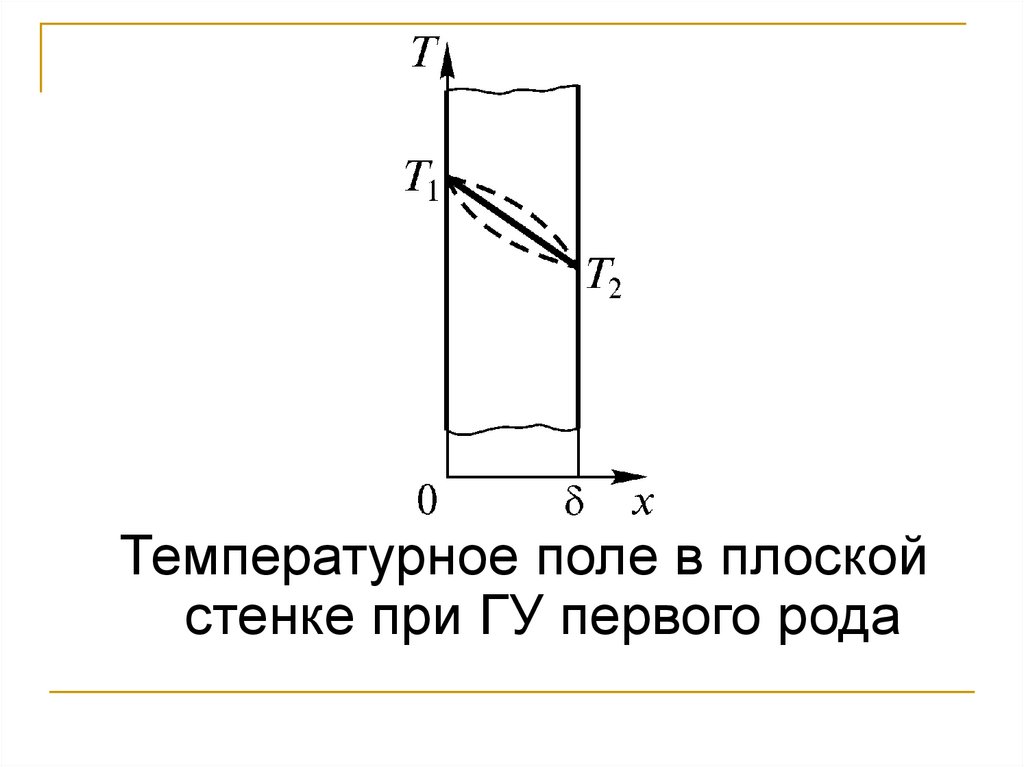
96.

Температурное поле в плоской
стенке при ГУ первого рода

97.

При граничных условиях первого рода:
Тогда:

98.

При граничных условиях второго рода:
-?
При граничных условиях второго рода задача имеет
бесчисленное множество решений

99.

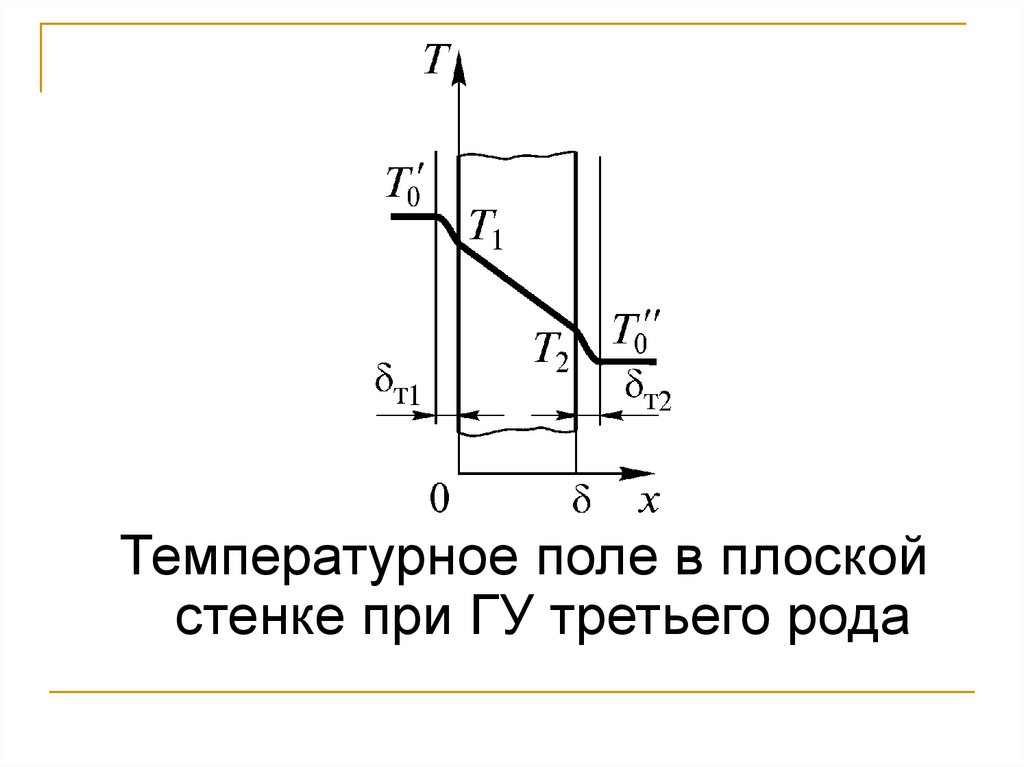
Температурное поле в плоской
стенке при ГУ третьего рода

100.

При граничных условиях третьего рода:
Откуда:
Коэффициент теплопередачи:

101.

Уравнение теплопроводности в стационарном режиме для
цилиндрической стенки:
Постоянные интегрирования зависят от граничных условий

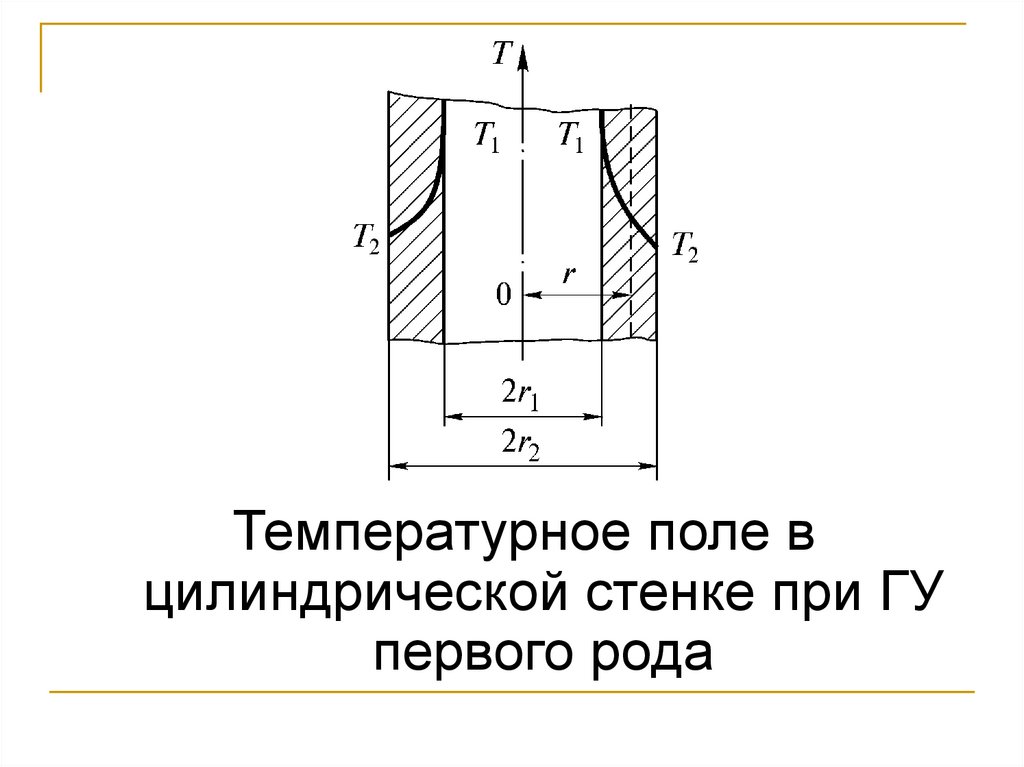
102.

Температурное поле в
цилиндрической стенке при ГУ
первого рода

103.

При граничных условиях первого рода:
Тогда:

104.

При граничных условиях второго рода:
-?
При граничных условиях второго рода задача имеет
бесчисленное множество решений

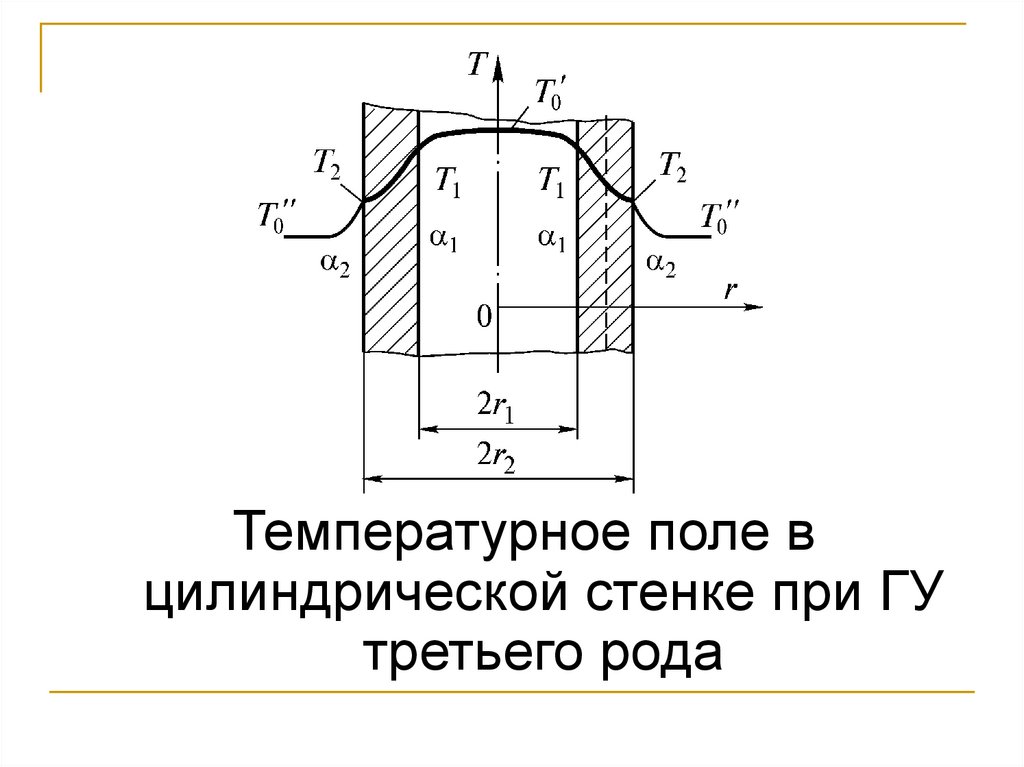
105.

Температурное поле в
цилиндрической стенке при ГУ
третьего рода

106.

При граничных условиях третьего рода:

107.

При граничных условиях третьего рода в случае многослойной
плоской стенки коэффициент теплопередачи:
При граничных условиях третьего рода в случае многослойной
цилиндрической стенки коэффициент теплопередачи:

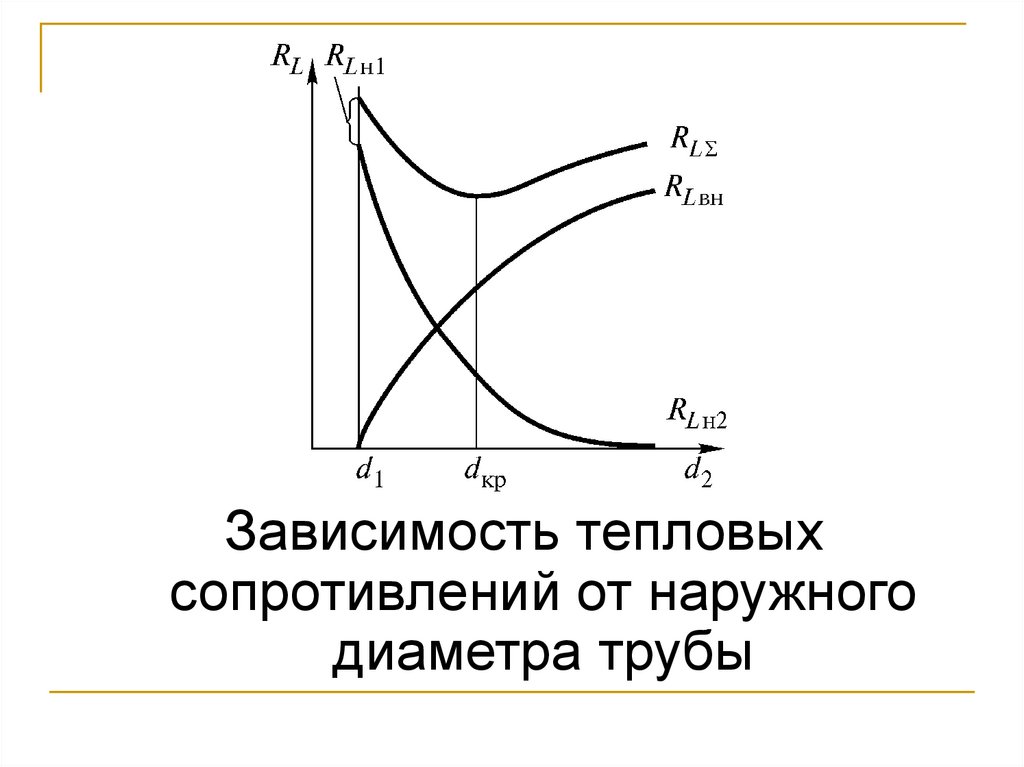
108.

Критический диаметр теплоизоляции
При граничных условиях третьего рода для цилиндрической
стенки тепловое сопротивление:
При этом, если d1=const, а d2 растет, то:
-?

109.

Зависимость тепловых
сопротивлений от наружного
диаметра трубы

110.

Дифференцируя выражение для теплового сопротивления по d2:
Эффективная теплоизоляция:
- диаметр неизолированного трубопровода

111.

Лекции 27-34

112.

Уравнение теплопроводности в нестационарном режиме:
Будем искать решение уравнения в виде:
Подставляя в исходное уравнение получим:

113.

Тогда решение имеет вид:
Константа D=0, тогда:
Константы C и k определяются из граничных условий

114.

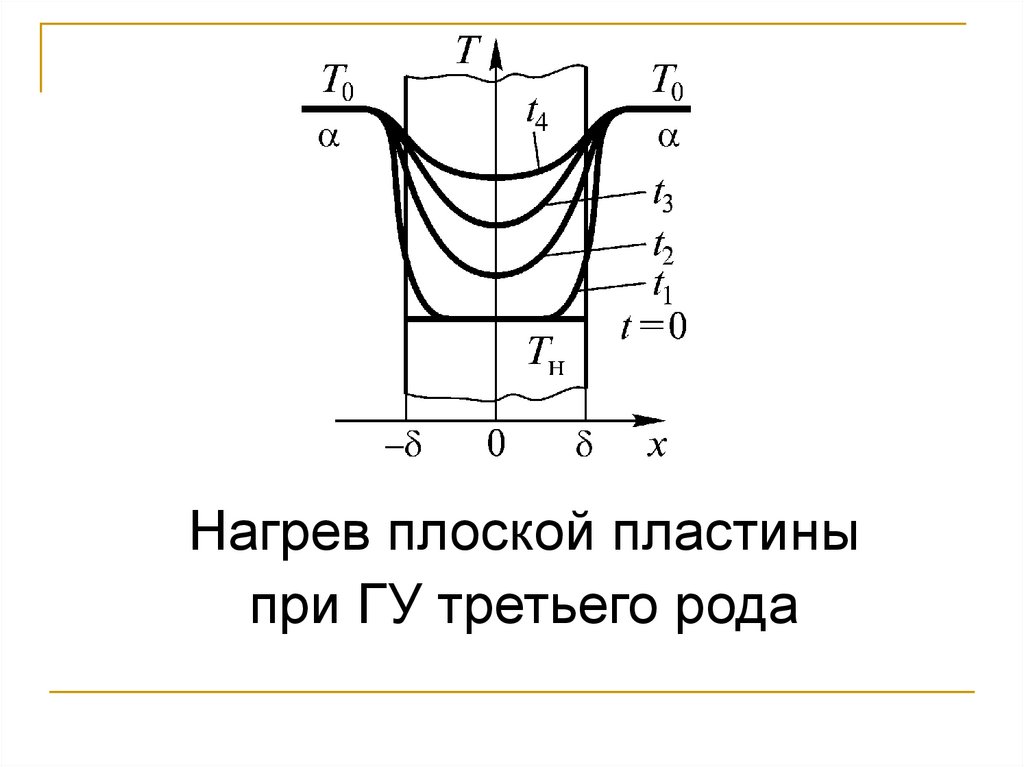
Нагрев плоской пластины
при ГУ третьего рода

115.

При граничных условиях третьего рода:
Введем избыточную температуру:
Уравнение теплопроводности примет вид:
Значит решение записывается в виде:
= (х, t) = С ехр (–k2at) cos (kx)

116.

При х= -δ:
μ
Bi
Fo

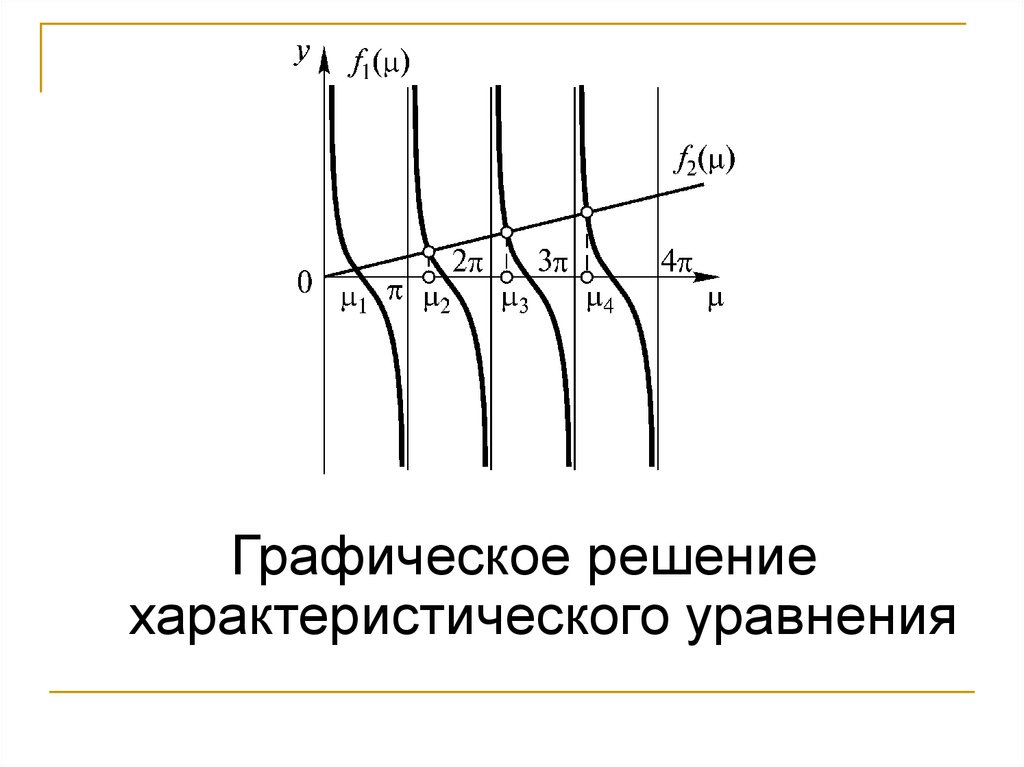
117.

Графическое решение
характеристического уравнения

118.

Константу Сn найдем из следующих соображений:
При m=n:

119.

Окончательно решение имеет вид:
Или в безразмерном виде:
где
Таким образом
Критерий Био

120.

а) нагрев термически тонких тел Bi→0
=
Т.к.

121.

Покажем, что результат справедлив для всех термически тонких
тел. Составим уравнение теплового баланса:
Введем избыточную температуру:
Тогда:
Введем характерный размер l:
Учтем, что

122.

Интегрируя получим:
где К – коэффициент формы
К=1 – для пластины
К=2 – для цилиндра
К=3 – для шара

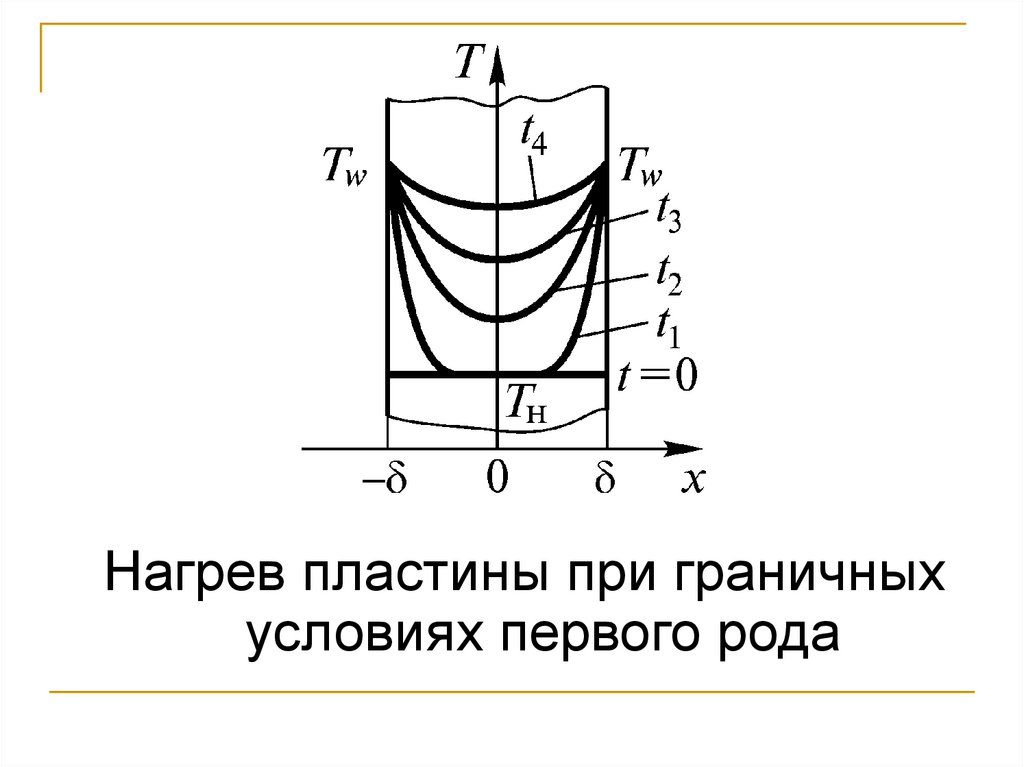
123.

Нагрев пластины при граничных
условиях первого рода

124.

б) Bi→∞, граничные условия первого рода
При Bi→∞ ctgμn=0, тогда
При этом
Тогда решение принимает вид:

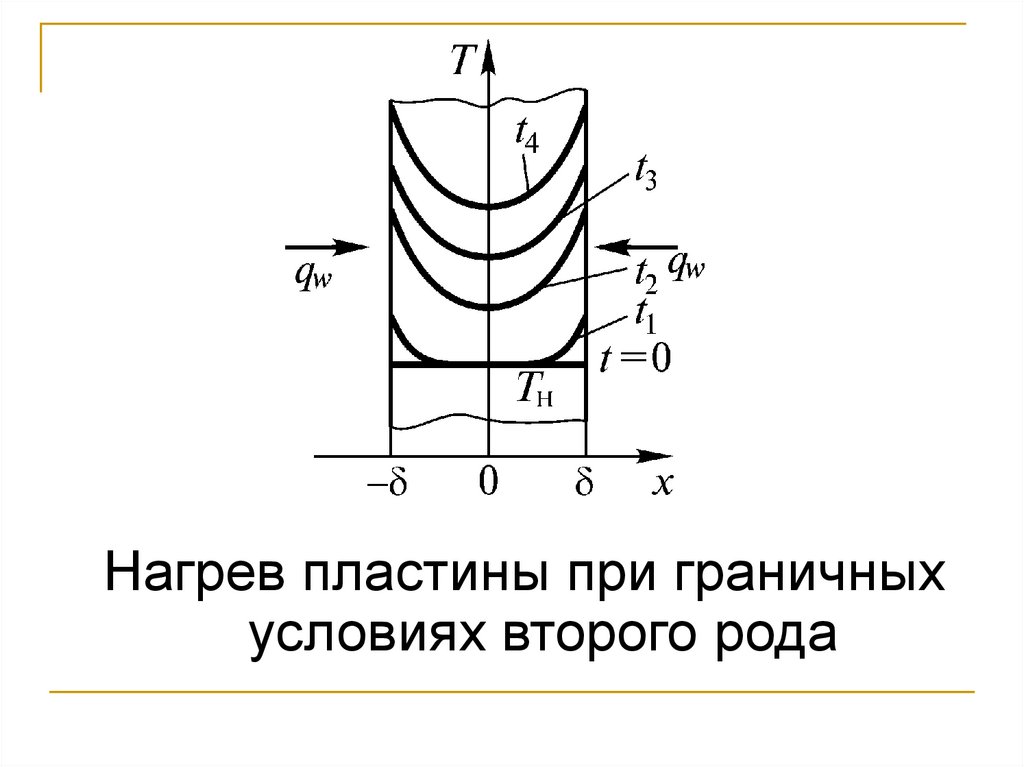
125.

Нагрев пластины при граничных
условиях второго рода

126.

При граничных условиях второго рода:
Введем новую переменную:
Продифференцируем по х исходное уравнение:
Так как:

127.

Имеем:
Решение будет иметь вид:
После подстановки:

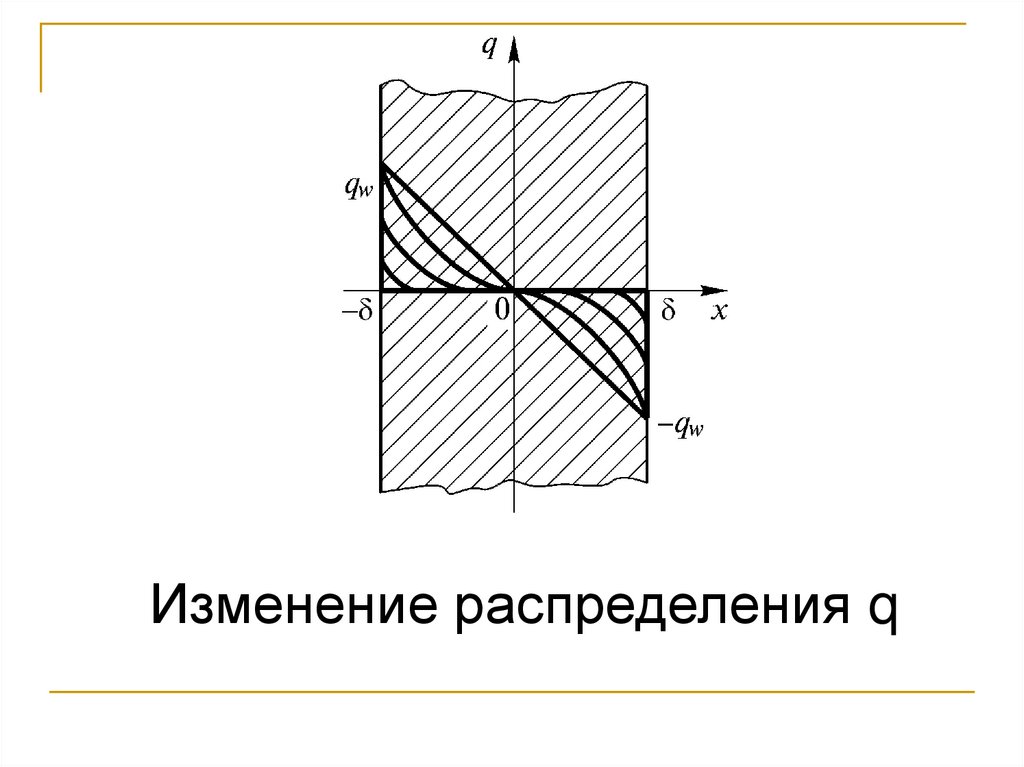
128.

Изменение распределения q

129.

Найдем функцию φ(t). Запишем закон сохранения энергии:
φ(t)
Окончательно решение имеет вид:
При Fo>0,3 наступает регулярный тепловой режим

130.

Регулярный тепловой режим при граничных условиях третьего рода
При Fo>0,3 решение уравнения теплопроводности имеет вид:
D1
Возьмем логарифм от этого выражения:
Обозначим темп нагрева через
Тогда дифференцируя получим:

131.

Регулярный тепловой режим при граничных условиях первого рода
При Fo>0,3 решение уравнения теплопроводности имеет вид:
Возьмем логарифм от этого выражения:
Обозначим темп нагрева при ГУ первого рода
Тогда дифференцируя получим:

132.

Темп нагрева при ГУ первого рода для тел различной формы
- для плоской пластины
- для шара
- для параллелепипеда
- для цилиндра

133.

Исследование нестационарной теплопроводности
методами теории подобия
Введем избыточную температуру
Тогда:

134.

Введем безразмерные величины
С учетом этого система приобретает вид
То есть