Узы дружбы в мире чисел. Исследовательская работа. 9 класс

1. «Узы дружбы в мире чисел»

Исследовательская работа
Ученика 9 «Б» класса гимназии №23
Пчелинцева Алексея

2. Введение

Цель:
изучить историю
дружественных
чисел и выяснить
вклад Леонарда
Эйлера в решение
проблемы
дружественных
чисел.
Задачи:
изучить литературу по
данному вопросу;
составить список
математиков,
открывших пары
дружественных чисел;
оценить вклад Л.Эйлера
в отыскание
дружественных чисел.

3. История дружественных чисел до Леонарда Эйлера

1. Античный период.
2. Арабский период.
3. Французский период.

4. Античный период

Дружественными назвали пары чисел, из
которых каждое равнялось сумме делителей
другого.
Первый документ:
«Изложение пифагорейского учения», 3-ий
век н.э., Ямвлих из Хальциса.
220 = 22 • 5 • 11, 220 = 1 + 2 + 4 + 71 + 142;
284 = 22 • 71, 284 = 1 + 2 + 4 + 5 +10 + 11 + 20 + 22 + 44+
+ 55 + 110.
Вывод: в античный период было дано
определение дружественных чисел и найдена
единственная пара таких чисел .

5. Арабский период

Теорема Сабита.
Если все три числа
p = 3 · 2n-1 – 1,q = 3 · 2n - 1 и r = 9 · 2n-1 – 1 –
простые, то числа А = 2n · р · q и В = 2n · r –
дружественные.
«Числа 17 296 и 18 416 являются
дружественными; одно из них избыточно,
другое недостаточно. Аллах всеведущ».
ибн аль – Банна (1300 г.)
Вывод: в арабский период была
сформулирована важнейшая теорема в
истории дружественных чисел и найдена
вторая пара таких чисел.

6. Французский период

Пьер Ферма в 1636 г.
и Рене Декарт в
1638 г.
«переоткрыли»
формулы Сабита и
вывели формулу,
дающую сумму
делителей числа по
его представлению в
виде произведения
степеней простых
чисел.
Рене Декарт в 1638
году открыл пару
дружественных чисел:
9 363 584 и 9 437 056.
Поиск дружественных
чисел способствовал
открытию малой
теоремы Ферма.
Вывод: французский период
охарактеризовался
открытием третьей пары
дружественных чисел.

7. Вклад Леонарда Эйлера в решение проблемы дружественных чисел

Эйлер искал
дружественные числа
двух видов:
А = 2n · p · q и
B = 2n · r;
А=а·p·q и
B=a·r
с простыми p, q, r.
С 1747 г. по 1750 г. Л.Эйлер
открыл 59 новых пар
дружественных чисел.
Вывод: за три года работы
Л. Эйлер открыл в 20 раз
больше пар
дружественных чисел,
чем за 20 веков до него.
Методы Эйлера:
Задавшись общим
множителем а, получал
для определения p и q
диофантово уравнение
второй степени;
Задавшись двумя из
трех простых чисел p, q,
r, искал подходящий
общий множитель а;
Задавшись всеми тремя
простыми числами,
искал подходящий
общий множитель а.

8. Значение работ Л.Эйлера по проблеме дружественных чисел для развития математики в целом

Тождества Макдональда
частный случай
(1972)
Формула Якоби (1928)
частный случай
поиски доказательства
эмпирический путь
Обширные вычисления
Л.Эйлера, связанные
с дружественными числами
(важная роль в теории эллиптических функций)
Тождество Эйлера
Рекуррентная формула Эйлера
для суммы делителей

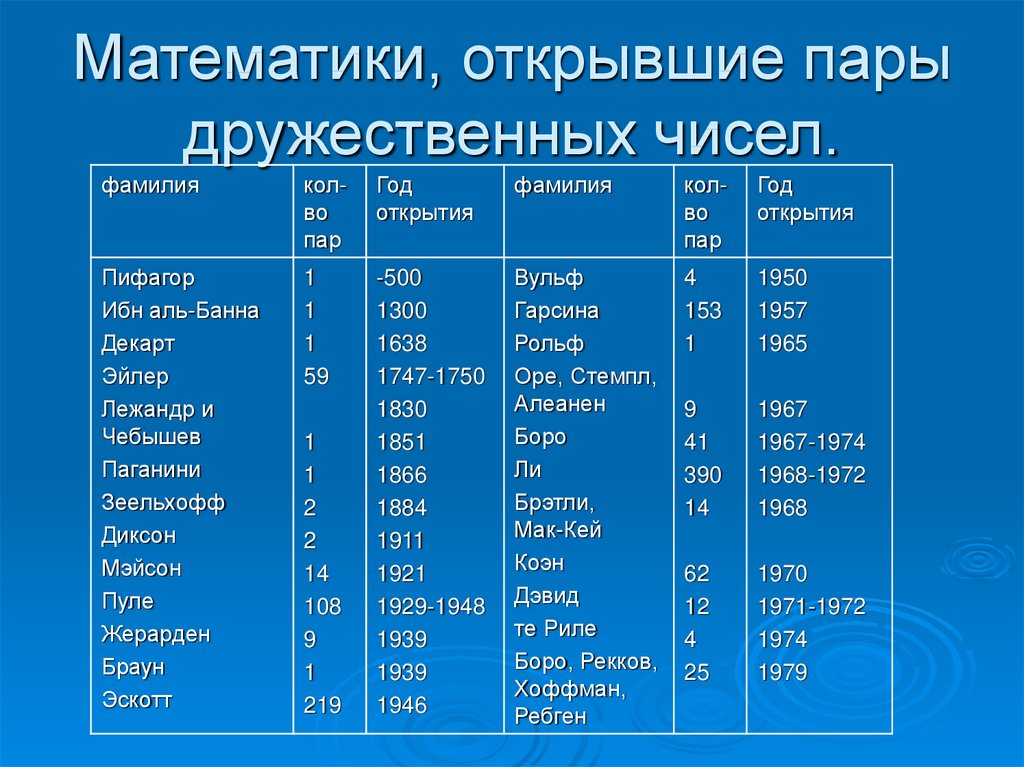
9. Математики, открывшие пары дружественных чисел.

фамилия
колво
пар
Год
открытия
фамилия
колво
пар
Год
открытия
Пифагор
Ибн аль-Банна
Декарт
Эйлер
Лежандр и
Чебышев
Паганини
Зеельхофф
Диксон
Мэйсон
Пуле
Жерарден
Браун
Эскотт
1
1
1
59
-500
1300
1638
1747-1750
1830
1851
1866
1884
1911
1921
1929-1948
1939
1939
1946
Вульф
Гарсина
Рольф
Оре, Стемпл,
Алеанен
Боро
Ли
Брэтли,
Мак-Кей
Коэн
Дэвид
те Риле
Боро, Рекков,
Хоффман,
Ребген
4
153
1
1950
1957
1965
9
41
390
14
1967
1967-1974
1968-1972
1968
62
12
4
25
1970
1971-1972
1974
1979
1
1
2
2
14
108
9
1
219