Модели и моделирование. Тема 1

1. Модели и моделирование

Тема 1. Модели и их типы
© К.Ю. Поляков, 2007-2011

2.

Модели в нашей жизни
2

3.

Что такое модель?
Модель – это объект, который обладает некоторыми
свойствами другого объекта (оригинала) и используется
вместо него.
Оригиналы и модели
Первый линейный русский корабль «Гото Предестинация»
3

4.

Что можно моделировать?
Модели объектов:
• уменьшенные копии зданий, кораблей, самолетов, …
• модели ядра атома, кристаллических решеток
• чертежи
•…
Модели процессов:
• изменение экологической обстановки
• экономические модели
• исторические модели
•…
Модели явлений:
• землетрясение
• солнечное затмение
• цунами
•…
4

5.

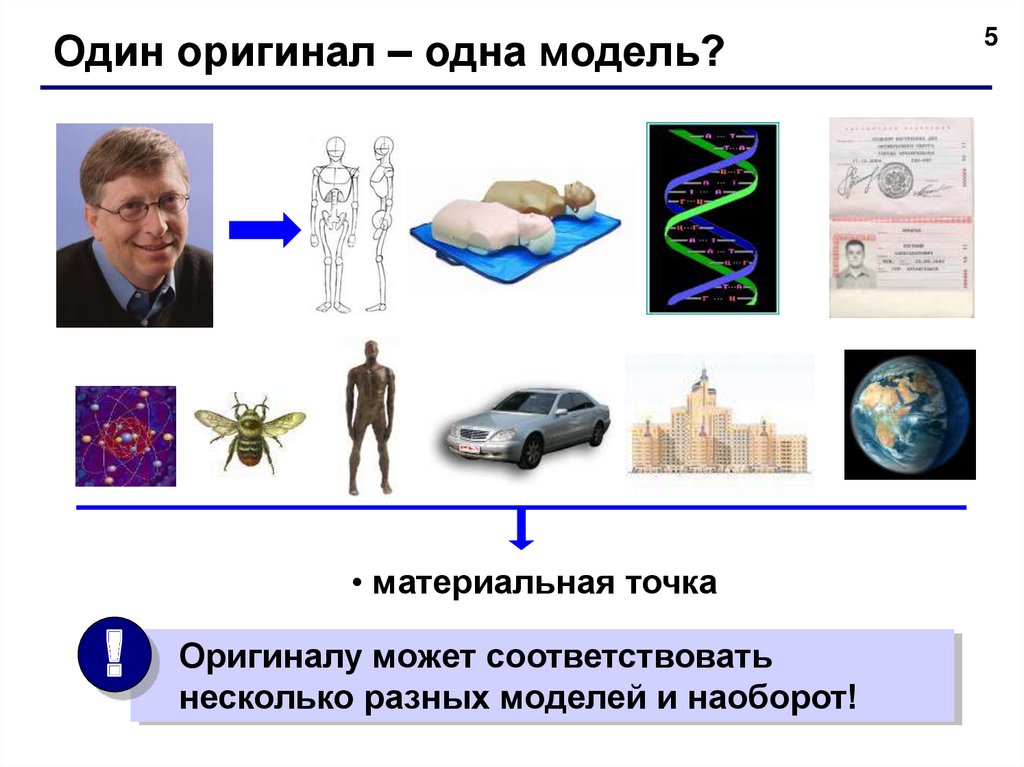
Один оригинал – одна модель?
• материальная точка
!
Оригиналу может соответствовать
несколько разных моделей и наоборот!
5

6.

6
Зачем нужно много моделей?
!
Тип модели определяется целями моделирования!
изучение
наследственности
изучение
строения
тела
примерка
одежды
учет граждан
страны
тренировка
спасателей

7.

Природа моделей
• материальные (физические, предметные) модели:
• информационные модели представляют собой
информацию о свойствах и состоянии объекта,
процесса, явления, и его взаимосвязи с внешним миром:
• вербальные – словесные или мысленные
• знаковые – выраженные с помощью формального языка
графические (рисунки, схемы, карты, …)
табличные
математические (формулы)
логические (различные варианты выбора действий на
основе анализа условий)
специальные (ноты, химические формулы)
7

8.

Модели по области применения
• учебные (в т.ч. тренажеры)
• опытные – при создании новых технических средств
аэродинамическая труба
испытания в опытовом бассейне
• научно-технические
имитатор солнечного
излучения
вакуумная камера в Институте
космических исследований
вибростенд
НПО «Энергия»
8

9.

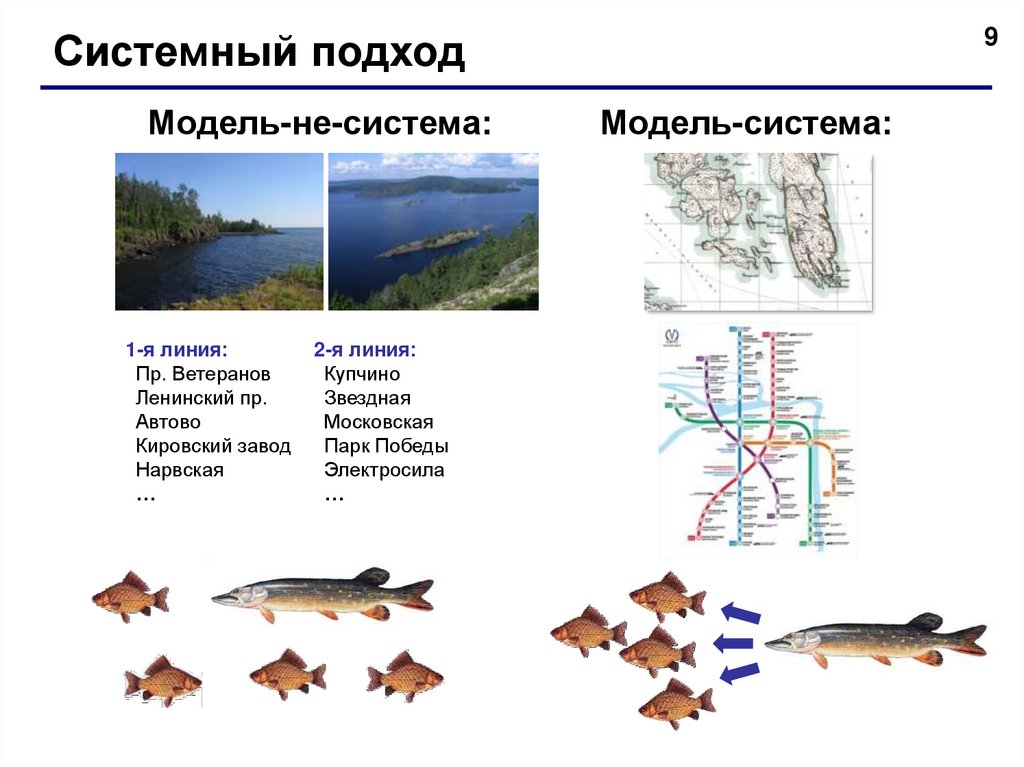
9
Системный подход
Модель-не-система:
1-я линия:
Пр. Ветеранов
Ленинский пр.
Автово
Кировский завод
Нарвская
…
2-я линия:
Купчино
Звездная
Московская
Парк Победы
Электросила
…
Модель-система:

10.

V. Проверка практикой, анализ результатов
Возможные выводы:
• задача решена, модель адекватна
• необходимо изменить алгоритм или условия
моделирования
• необходимо изменить модель (например,
учесть дополнительные свойства)
• необходимо изменить постановку задачи
10

11.

11
Пример.
Задача. Обезьяна хочет
сбить бананы на
пальме. Как ей надо
кинуть кокос, чтобы
попасть им в бананы.
Анализ задачи:
• все ли исходные
данные известны?
• есть ли решение?
• единственно ли
решение?

12.

I. Постановка задачи
12
Допущения:
• кокос и банан считаем материальными точками
• расстояние до пальмы известно
• рост обезьяны известен
• высота, на которой висит банан, известна
• обезьяна бросает кокос с известной начальной
скоростью
• сопротивление воздуха не учитываем
При этих условиях требуется найти начальный угол, под
которым надо бросить кокос.
?
Всегда ли есть решение?

13.

13
II. Разработка модели
Графическая модель
y
V
H
h
x
L
Формальная (математическая) модель
x V cos t ,
gt 2
y h V sin t
2
Задача: найти t, , при которых
V cos t L,
gt 2
h V sin t
H
2

14.

III. Тестирование модели
Математическая модель
x V cos t
gt 2
y h V sin t
2
• при нулевой скорости кокос падает вертикально вниз
• при t=0 координаты равны (0,h)
• при броске вертикально вверх ( =90o) координата x не
меняется
• при некотором t координата y начинает уменьшаться
(ветви параболы вниз)
!
Противоречий не обнаружено!
14

15.

15
IV. Эксперимент
Метод I.
Меняем угол . Для выбранного угла строим
траекторию полета ореха. Если она проходит выше
банана, уменьшаем угол, если ниже – увеличиваем.
Метод II.
Из первого равенства выражаем время полета:
V cos t L
L
t
V cos
Меняем угол . Для выбранного угла считаем t, а
затем – значение y при этом t. Если оно больше H,
уменьшаем угол, если меньше – увеличиваем.
не надо строить всю траекторию для каждого

16.

V. Анализ результатов
1. Всегда ли обезьяна может сбить банан?
2. Что изменится, если обезьяна может бросать кокос с
разной силой (с разной начальной скоростью)?
3. Что изменится, если кокос и бананы не считать
материальными точками?
4. Что изменится, если требуется учесть сопротивление
воздуха?
5. Что изменится, если дерево качается?
16

17. Модели и моделирование

Тема 3. Модели биологических систем
(по мотивам учебника А.Г. Гейна и др., Информатика и ИКТ,
10 класс, М.: Просвещение, 2008)
© К.Ю. Поляков, 2007-2011

18.

18
Модель деления
N
i
N 0 – начальная численность
N 2 N0
N1 2N 0 – после 1 цикла деления
N 2 2 N1 4 N0 – после 2-х циклов
i
N0
N i 2 N i 1 2 N 0
Особенности модели:
1) не учитывается смертность
2) не учитывается влияние внешней среды
3) не учитывается влияние других видов
i

19.

19
Модель неограниченного роста (T. Мальтус)
N i N i 1 K p N i 1 K c N i 1
Kp
Kc
– коэффициент рождаемости
– коэффициент смертности
Коэффициент
прироста
N
K K p Kc
Ni (1 K ) Ni 1
Ni Ni 1 K Ni 1
K 0
K 0
N0
прирост
K 0
Особенности модели:
1) не учитывается влияние численности N и внешней
среды на K
2) не учитывается влияние других видов на K
i

20.

Модель ограниченного роста (П. Ферхюльст)
L – предельная численность животных
Ni (1 K L ) Ni 1
Идеи:
1) коэффициент прироста KL зависит от численности N
2) при N=0 должно быть KL=K (начальное значение)
3) при N=L должно быть KL=0 (достигнут предел)
L N i 1
N i 1 K
N i 1
L
!
Модель адекватна,
если ошибка < 10%!
N
L
N0
i
20

21.

21
Модель с отловом
Примеры: рыбоводческое хозяйство, разведение
пушных зверей и т.п.
L N i 1
N i 1 K
N i 1 R
L
?
отлов
Какая будет численность?
N i N i 1, прирост = отлову
L N
N N K
N R
L
?
K
N2 K N R 0
L
Сколько можно отловить?

22.

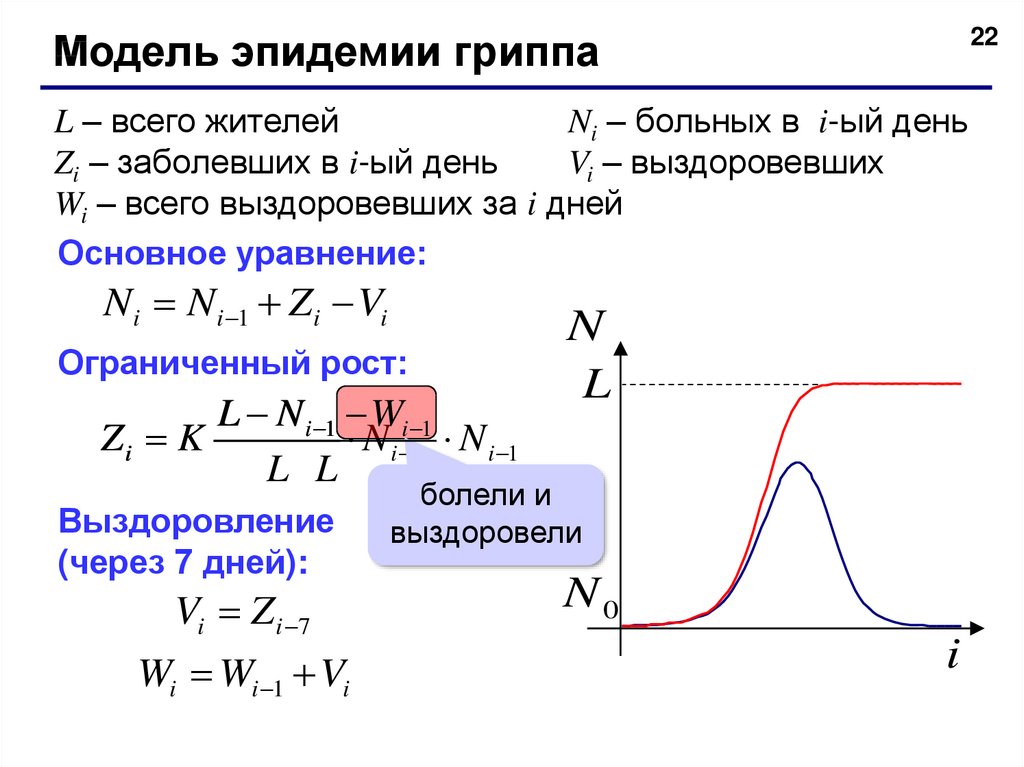
22
Модель эпидемии гриппа
L – всего жителей
Ni – больных в i-ый день
Zi – заболевших в i-ый день
Vi – выздоровевших
Wi – всего выздоровевших за i дней
Основное уравнение:
Ni Ni 1 Zi Vi
Ограниченный рост:
L N i 1 Wi 1
Zi K
N i 1 N i 1
L L
Выздоровление
(через 7 дней):
Vi Z i 7
Wi Wi 1 Vi
N
L
болели и
выздоровели
N0
i

23.

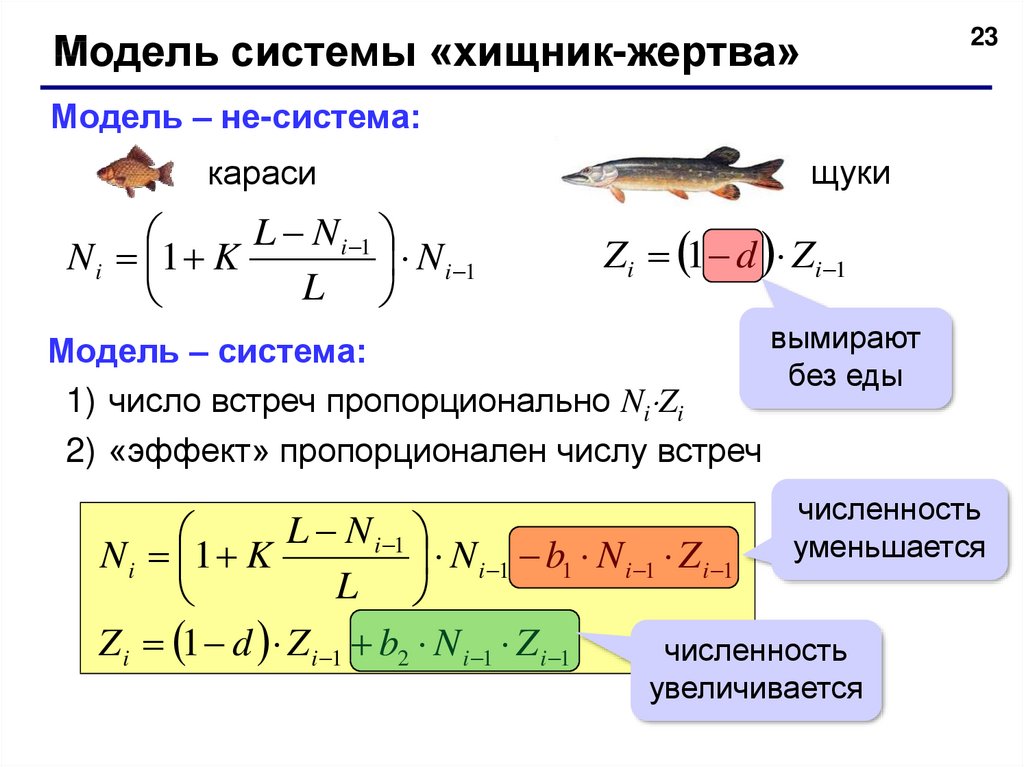
23
Модель системы «хищник-жертва»
Модель – не-система:
караси
L N i 1
N i 1 K
N i 1
L
щуки
Zi 1 d Zi 1
вымирают
Модель – система:
без еды
1) число встреч пропорционально Ni Zi
2) «эффект» пропорционален числу встреч
численность
уменьшается
L N i 1
N i 1 K
N i 1 b1 N i 1 Z i 1
L
Z i 1 d Z i 1 b2 N i 1 Z i 1
численность
увеличивается

24.

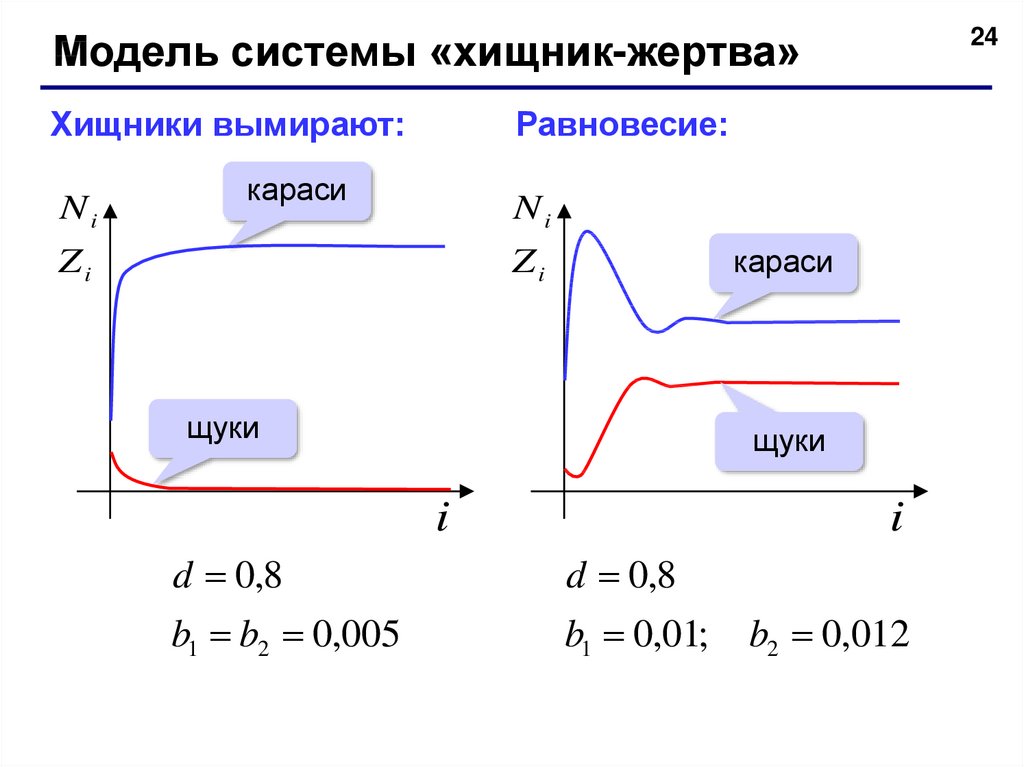
24
Модель системы «хищник-жертва»
Хищники вымирают:
Ni
Равновесие:
караси
Ni
Zi
караси
Zi
щуки
щуки
i
d 0,8
b1 b2 0,005
i
d 0,8
b1 0,01;
b2 0,012

25.

25
120,00
100,00
80,00
60,00
Жертвы
Хищники
40,00
20,00
0,00
0
10
20
30
40
50
60

26.

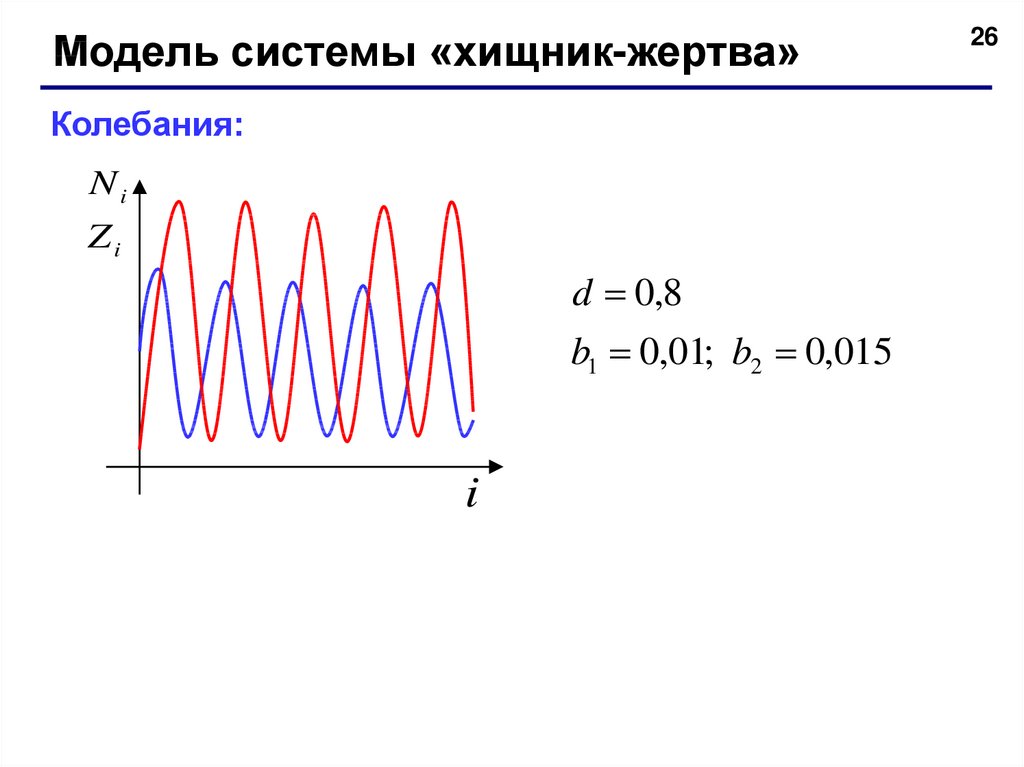
Модель системы «хищник-жертва»
Колебания:
Ni
Zi
d 0,8
b1 0,01; b2 0,015
i
26

27.

Конец фильма
27