Cutting a Pie is Not a Piece of Cake

1. Cutting a Pie is Not a Piece of Cake

Walter Stromquist
Swarthmore College
[email protected]
Third World Congress of the Game Theory Society
Evanston, IL
July 13, 2008
1

2. Cutting a Pie is Not a Piece of Cake Julius B. Barbanel, Steven J. Brams, Walter Stromquist

Mathematicians enjoy cakes for their own sake and as a metaphor
for more general fair division problems.
A cake is cut by parallel planes into n pieces, one for each of n
players whose preferences are defined by separate measures. It is
known that there is always an envy-free division, and that such a
division is always Pareto optimal. So for cakes, equity and efficiency
are compatible.
A pie is cut along radii into wedges. We show that envy-free
divisions are not necessarily Pareto optimal --- in fact, for some
measures, there may be no division that is both envy-free and Pareto
optimal. So for pies, we may have to choose between equity and
efficiency.
2

3.

This is joint work with
Julius B. Barbanel (Union College)
Steven J. Brams (New York University)
3

4.

1. Introduction
2. Cakes
3. Pies
4. Summary
4

5.

5

6. Some definitions

Cakes are cut by parallel planes.
The cake is an interval C = [ 0, m ].
Points in interval = possible cuts.
Subsets of interval = possible pieces.
We want to partition the interval into S1, S2, …, Sn, where
Si = i-th player’s piece.
Player’s preferences are defined by measures v1, v2, …, vn
vi (Sj ) = Player i’s valuation of piece Sj.
These are probability measures.
We always assume that they are non-atomic (single points always
have value zero).
6

7. “Absolutely continuous”

Sometimes we assume that the measures are absolutely continuous
with respect to each other.
In effect, this assumption means that pieces with positive length
also have positive value to every player.
7

8.

1. Introduction
2. Cakes
3. Pies
4. Summary
8

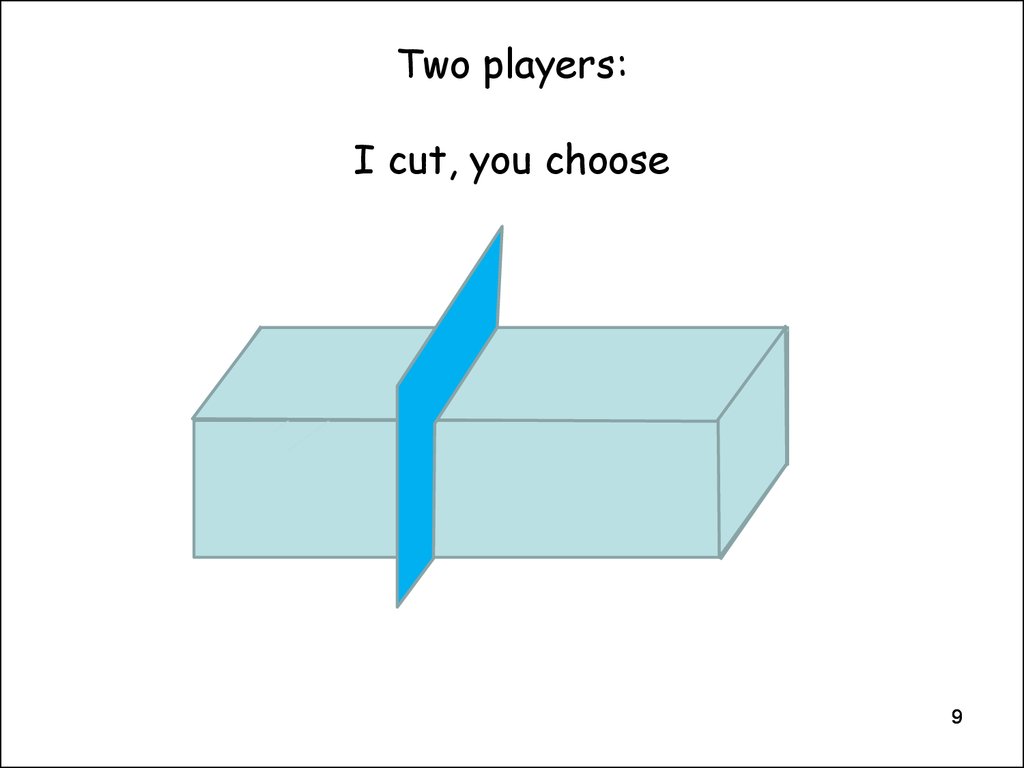
9. Two players: I cut, you choose

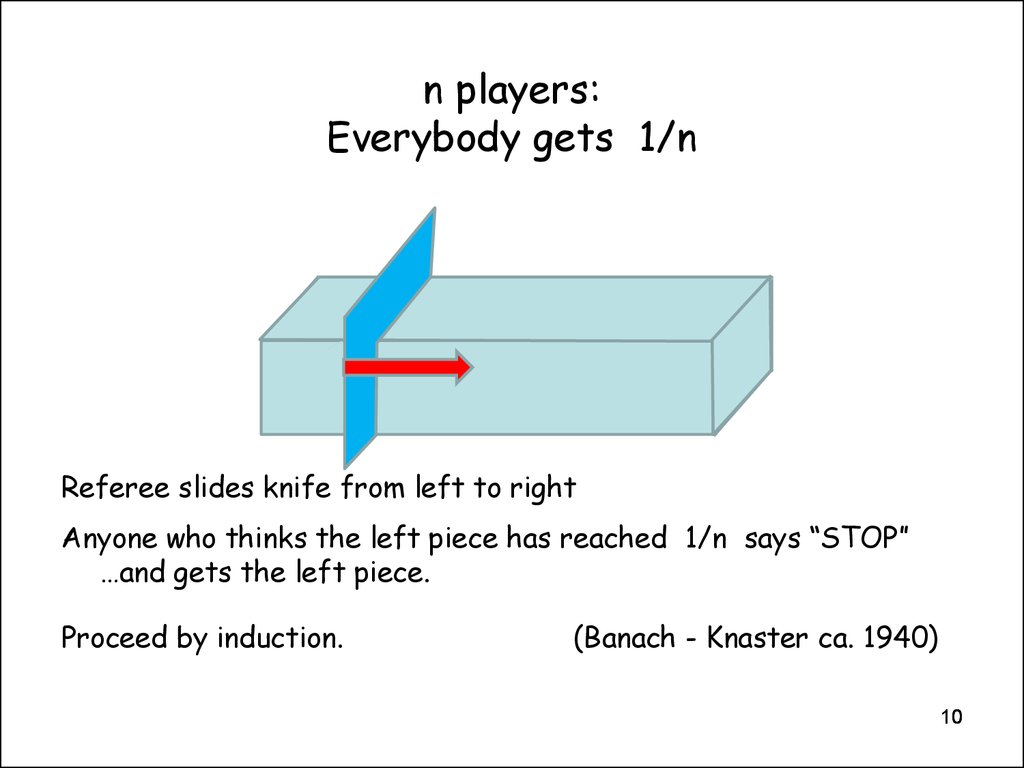
9

10. n players: Everybody gets 1/n

Referee slides knife from left to right
Anyone who thinks the left piece has reached 1/n says “STOP”
…and gets the left piece.
Proceed by induction.
(Banach - Knaster ca. 1940)
10

11. Envy-free divisions

A division is envy-free if no player thinks any other player’s piece
is better than his own:
vi (Si) vi (Sj)
for every i and j.
Can we always find an envy-free division?
Theorem (1980): For n players, there is always an envy-free
division in which each player receives a single interval.
Proofs:
(WRS) The “division simplex”
(Francis Edward Su) Sperner’s Lemma
11

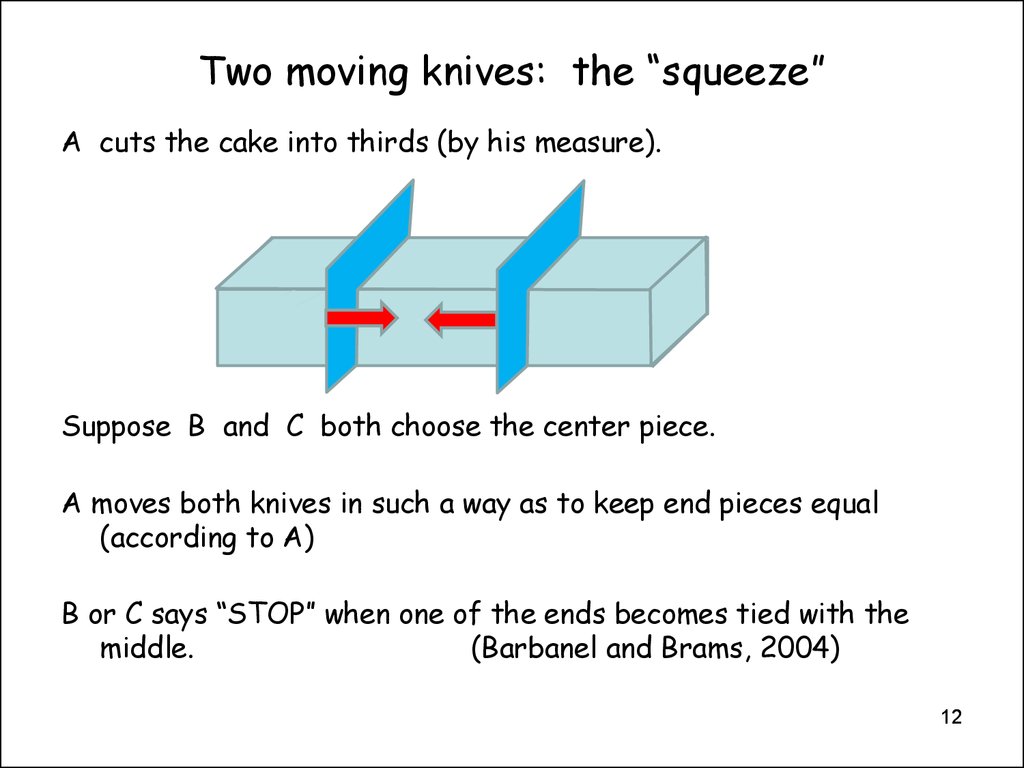
12. Two moving knives: the “squeeze”

A cuts the cake into thirds (by his measure).
Suppose B and C both choose the center piece.
A moves both knives in such a way as to keep end pieces equal
(according to A)
B or C says “STOP” when one of the ends becomes tied with the
middle.
(Barbanel and Brams, 2004)
12

13. Undominated allocations

A division {Si} = S1, S2, …, Sn is dominated by a division
{Ti} = T1, T2, …, Tn if
vi(Ti) vi(Si)
for every i
with strict inequality in at least one case.
That is: T makes some player better off, and doesn’t make any
player worse off.
{Si} is undominated if it isn’t dominated by any {Ti} .
“undominated” = “Pareto optimal” = “efficient”
13

14. Envy-free implies undominated

Is there an envy-free allocation that is also undominated?
Theorem (Gale, 1993): Every envy-free division of a cake into n
intervals for n players is undominated (assuming absolute
continuity).
So for cakes: EQUITY EFFICIENCY.
14

15. Gale’s proof

Theorem (Gale, 1993): Every envy-free division of a cake into n
intervals for n players is undominated.
Proof: Let {Si} be an envy-free division.
Let {Ti} be some other division that we think might
dominate {Si}.
S2
S3
S1
T3
T1
T2
v1(T1) < v1(S3) v1(S1)
so {Ti} doesn’t dominate {Si} after all. //
15

16. Cakes without absolute continuity

First player’s preference: Uniform, EXCEPT on the leftmost third
of the cake. The first player likes only the left half of the
leftmost third.
All other players’ preferences are uniform.
The only envy-free divisions involve cutting the pie in thirds.
None of these divisions is undominated.
Without absolute continuity: We may have to choose between
envy-free and undominated.
16

17. Summary for cakes

With absolute continuity:
There is always an envy-free division.
Every envy-free division is also undominated.
There is always a division that is both envy-free and undominated.
Without absolute continuity:
There is always an envy-free division.
For some measures, there is NO division that is both envy-free
and undominated. We may have to choose!
Unless n = 2, when there is always an envy-free, undominated
division, whatever the measures.
17

18.

1. Introduction
2. Cakes
3. Pies
4. Summary
18

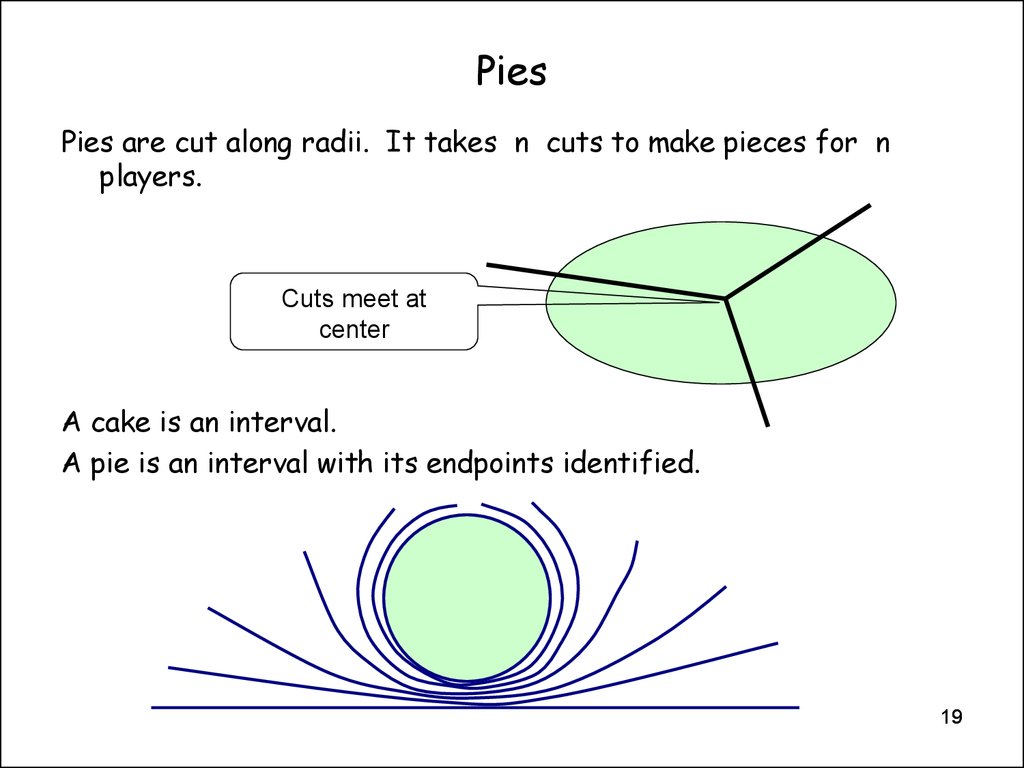
19. Pies

Pies are cut along radii. It takes n cuts to make pieces for n
players.
Cuts meet at
center
A cake is an interval.
A pie is an interval with its endpoints identified.
19

20.

1
3
1
3
2
2
20

21. Pies

1. Are there envy-free divisions for pies?
YES
2. Does Gale’s proof work?
NO
Envy-free does NOT imply undominated
3. Are there pie divisions that are both envy-free and
undominated? (“Gale’s question,” 1993)
YES for two players
NO if we don’t assume absolute continuity
NO for the analogous problem with unequal claims
(Brams, Jones, Klamler – next talk!)
21

22. Pies

For n 3, there are measures for which there does NOT exist an
envy-free, undominated allocation.
These measures may be chosen to be absolutely continuous.
So, Gale’s question is answered in the negative.
22

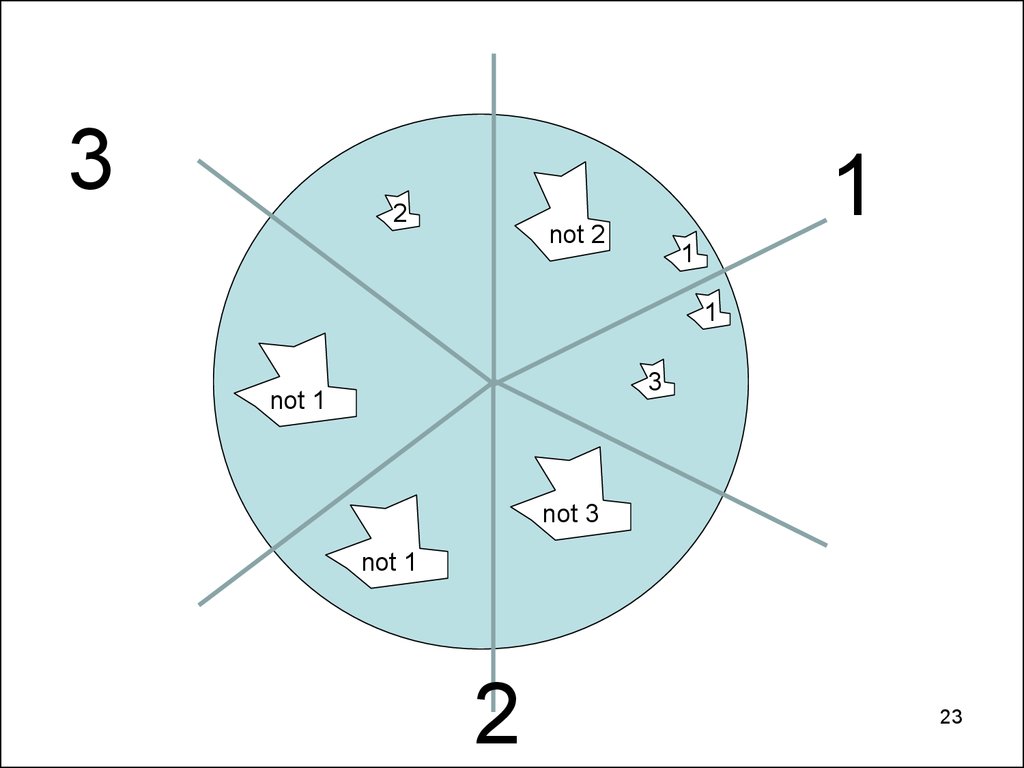
23.

3
2
1
not 2
1
1
3
not 1
not 3
not 1
2
23

24. The example

Partition the pie into 18 tiny sectors.
Each player’s preference is uniform, except…
Each player dislikes certain sectors (grayed out).
Each player perceives positive or negative bonuses (C)
or mini-bonuses ( ) in certain sectors.
The measures for three players:
–C
+C
–
+C
–C
+
–C
+
+C
–C
+C
–
+C
+C
24

25. Pies for two players

Of all envy-free allocations, pick the one most preferred
by Player 2.
That allocation is both envy-free and undominated.
25

26. Summary for pies

With or without absolute continuity:
There is always an envy-free division.
For some measures, there is NO division that is both envy-free
and undominated. We may have to choose!
Unless n = 2, when there is always an envy-free, undominated
division, whatever the measures.
26

27.

1. Introduction
2. Cakes
3. Pies
4. Summary
27

28. Summary: When must there be an envy-free, undominated allocation?

2 players
3 players
CAKE
PIE
YES
YES
YES, assuming
absolute
continuity
(otherwise NO)
NO
28

29. Cookies

This cookie cutter has blades at fixed 120-degree angles.
But the center can go anywhere. Is there always an envy-free
division of the cookie? Envy-free and undominated?
29