Похожие презентации:
Определение. Примеры. Классификация и характеристика методов решения систем линейных уравнений
1. 1. Определение. Примеры. 2. Классификация и характеристика методов решения систем линейных уравнений. 3. СР № 4. Прямые методы
ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯСИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
(ОПОРНЫЙ КОНСПЕКТ С ОЦЕНКОЙ)
1. Определение. Примеры.
2. Классификация и характеристика
методов решения систем линейных
уравнений.
3. СР № 4. Прямые методы решения
СЛАУ: метод Крамера, матричный метод.
4. Пр. р. № 5.1 «Решение систем двух
уравнений с двумя неизвестными»
2. Определение. Примеры.
К решению систем линейных алгебраических уравненийсводятся многочисленные практические задачи (уравнения
материального баланса, уравнения теплового баланса,
численное решение краевых задач для дифференциальных
уравнений,
моделирование
некоторых
специальных
инженерных задач и др.).
Можно с полным основанием утверждать, что решение
линейных систем является одной из самых распространенных и
важных
задач
вычислительной
математики.
Конечно,
существует много методов и современных пакетов прикладных
программ для решения СЛАУ, но для того, чтобы их успешно
использовать, необходимо разбираться в основах построения
методов и алгоритмов, иметь представления о недостатках и
преимуществах используемых методов.
3.
1. Основные понятияСистема n линейных алгебраических уравнений может
быть записана в виде
a11 x1 a12 x2 ... a1n xn b1
a21 x1 a22 x1 ... a2 n xn b2
............................................
an1 x1 an 2 x2 ... ann xn bn
Совокупность коэффициентов этой системы
записать в виде следующей таблицы (матрицы)
a11a12 ...a1n
a a ...a
A 21 22 2 n
..................
an1an 2 ...ann
(1.1)
можно
(1.2)
4.
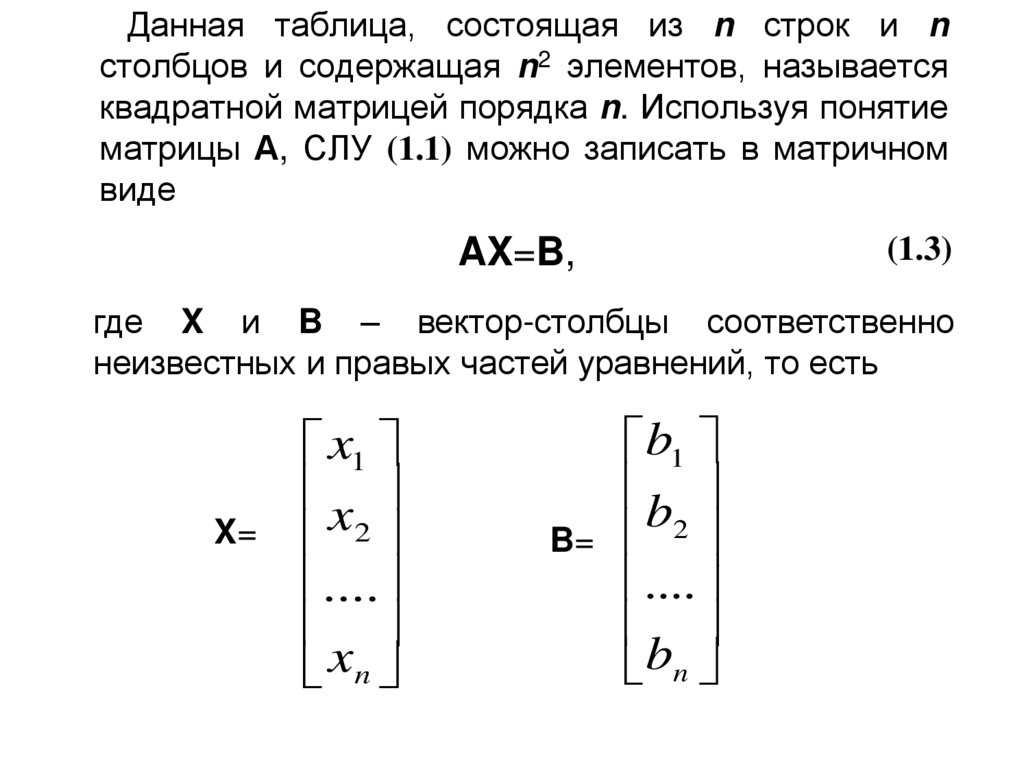
Данная таблица, состоящая из n строк и nстолбцов и содержащая n2 элементов, называется
квадратной матрицей порядка n. Используя понятие
матрицы А, СЛУ (1.1) можно записать в матричном
виде
(1.3)
AX=B,
где X и B – вектор-столбцы соответственно
неизвестных и правых частей уравнений, то есть
X=
x1
x
2
....
xn
B=
b1
b
2 .
....
b n
5.
Определителем (детерминантом) матрицы А n-го порядканазывается число D (иногда обозначают det A), равное
a11a12 ...a1n
D
a21a22 ...a2 n
...............
( 1) a1 a2 ...an ,
k
(1.4)
an1an 2 ...a nn
.
где индексы , ,..., пробегают все возможные n! перестановок
номеров 1, 2, ... ,n; k – число инверсий в данной перестановке.
Необходимым и достаточным условием существования
единственного решения СЛУ является условие D 0.
В случае D=0 матрица называется вырожденной, при этом
СЛУ (1.1) либо не имеет решения, либо имеет их бесчисленное
множество.
ПРИМЕЧАНИЕ. Матрица A−1 называется обратной по отношению к
квадратной матрице A, если их произведение равно единичной матрице:
AA−1 = A−1 A= E. Всякая невырожденная матрица A (т.е. с отличным от нуля
определителем) имеет обратную. При этом Det A−1=1/D.
6. 2. Классификация и характеристика методов решения систем линейных уравнений
Методы решения СЛУ делятся на две группы:прямые методы: (изучены в курсе высшей математики)
метод Гаусса;
метод Гаусса-Жордана;
метод Крамера;
матричный метод.
•итерационные методы:
метод простой итерации (метод Якоби);
метод Гаусса-Зейделя;
метод прогонки.
7.
Прямые методы решения СЛУПрямые методы используют конечные соотношения
(формулы) для вычисления неизвестных. Они дают решения
после выполнения заранее известного числа итераций. Эти
методы сравнительно просты и наиболее универсальны, т.е.
пригодны для решения широкого класса линейных систем
Недостатки прямых методов:
• требуют хранения в ОЗУ сразу всей матрицы А (при
больших n расходуется много места в памяти);
• не учитывают структуру матрицы А;
• накапливают погрешности в процессе решения, т.к.
вычисления на любом этапе используют результаты
предыдущих операций (это особенно опасно для систем
большой размерности, так как возрастает общее число
операций, а так же для плохо обусловленных систем,
очень чувствительных к погрешностям, в силу того, что в
них детерминант близок к нулю D≈0).
8.
Поэтому прямые методы используют обычнодля сравнительно не больших (n<200) СЛУ с плотной
матрицей и не близким к нулю детерминантом.
Прямые методы решения иногда называют точными,
т.к. решение выражается в виде точных формул через
коэффициенты СЛУ. Однако не нужно забывать, что
точное решение может быть получено лишь при точных
значениях коэффициентов системы, а так же при
выполнении вычислений с бесконечным числом
разрядов. На практике же, при использовании ЭВМ,
вычисления проводятся с ограниченным числом знаков,
определяемых
разрядностью
машины,
поэтому
неизбежны погрешности в окончательных результатах.
9. 2) Итерационные методы решения СЛУ
• Итерационнымиметодами
являются
методы
последовательных приближений. В них, как всегда,
нужно задать некоторое приближенное решение –
начальное приближение. После этого с помощью
некоторого
алгоритма
проводится
один
цикл
вычислений, называемый итерацией. В результате
итерации находят новое приближение. Итерации
проводятся до получения решения с требуемой
точностью.
• Алгоритмы итерационных методов обычно более
сложные по сравнению с прямыми методами. Объем
вычислений в них заранее определить трудно. Тем не
менее, итерационные методы в ряде случаев
предпочтительнее.
10. Достоинства итерационных методов:
• требуют хранения в памяти ЭВМ не всей матрицысистемы, а лишь нескольких векторов с n компонентами;
• погрешности окончательных результатов не накапливаются, т.к. точность вычислений в каждой итерации
определяется
лишь
результатами
предыдущей
итерации и практически не зависит от ранее выполненных вычислений.
• В силу указанных достоинств, итерационные методы
особенно полезны в случае большого числа уравнений,
а так же плохо обусловленных систем. При этом следует
отметить, что сходимость итераций может быть очень
медленной. В связи с этим, ищутся эффективные пути
ее ускорения.
• Итерационные методы полезно использовать для уточнения решений полученных с помощью прямых методов.
Такие смешанные алгоритмы обычно довольно
эффективны, особенно для плохо обусловленных
систем.
11. 3.3. Итерационные методы
1) Метод уточнения решенияРешения, полученные с помощью прямых методов, обычно
содержат погрешности, вызванные округлением при выполнении
операций на ЭВМ с ограниченным числом разрядов. Рассмотрим
один из методов уточнения решения, найденного прямым методом.
Пусть с помощью некоторого прямого метода вычислены
приближенные значения x1(0) , x2(0) ,..., xn(0) . Подставляя их в левые
части исходной системы (1.1), получим некоторые значения правой
(0)
части СЛУ bi отличные от bi (i=1,2,...,n):
a11x1( 0) a12 x2( 0) ... a1n xn( 0) b1( 0)
(0)
(0)
(0)
(0)
a
x
a
x
...
a
x
b
21 1
22 2
2n n
2
(3.4)
..........
..........
..........
..........
.......
a x ( 0) a x ( 0) ... a x ( 0) b ( 0)
n1 2
nn n
n
n1 1
(0)
(0)
Обозначим: i xi xi − погрешности значений неизвестных;
ri(0) bi bi(0) − невязки; i 1, n.
12.
Тогда, вычитая каждое уравнение системы (3.4) из соответствующего уравнения исходной системы (3.1), с учетом введенныхобозначений, получим:
(0)
(0)
a11 1(0) a12 (0)
...
a
r
2
1n n
1
(0)
(0)
(0)
(0)
a21 1 a22 2 ... a2 n n r2
...................................................
a (0) a (0) ... a (0) r (0)
n2 2
nn n
n
n1 1
(3.5)
Решая эту систему, найдём значения погрешностей i , которые
используем в качестве поправок к решению. Таким образом,
следующие приближения неизвестных имеют вид
(0)
(1)
(0)
(0)
x1(1) x1(0) 1(0) , x2(1) x2(0) (0)
,...,
x
x
2
n
n
n .
(3.6)
Таким же способом можно найти новые поправки к решению i
(2)
(1)
(1)
x
x
и следующие приближения переменных i
и т. д.
i
i
(1)
Процесс продолжается до тех пор, пока все очередные значения
погрешностей (поправок) не станут достаточно малыми: |εi |≤ E.
13.
Такой процесс уточнения решения представляетфактически итерационный метод решения СЛУ. При этом
для нахождения очередного приближения (на каждой
итерации) решаются СЛУ вида (3.5) с одной и той же
матрицей, являющейся матрицей исходной системы
уравнений, при разных правых частях. В результате
каждой итерации получаются новые значения неизвестных.
При малом (с заданной погрешностью E) изменении
этих значений на 2-х последовательных итерациях процесс
прекращается и происходит вывод значений неизвестных,
полученных на последней итерации. Для предотвращения
непроизводительных затрат компьютерного времени в
случае отсутствия сходимости в алгоритм вводят счётчик
числа итераций, при достижении некоторого числа которых
счёт прекращается.
14.
2) Метод Гаусса – ЗейделяОдин из самых простых и распространенных итерационных
методов, легко программируемых.
Рассмотрим метод на примере СЛУ 3-го порядка:
a11 x1 a12 x2 a13 x3 b1 ,
a21 x1 a22 x2 a23 x3 b2 ,
a x a x a x b .
32 2
33 3
3
31 1
(3.7)
Положим, что диагональные элементы aii (i=1,2,3) отличны от
нуля (иначе можно переставить уравнения). Выразим неизвестные
x1, x2, x3 соответственно из первого, второго и третьего уравнений
системы (3.7):
x1 1 a11 b1 a12 x2 a13 x3 ,
x2 1 a22 b2 a21 x1 a23 x3 ,
x3 1 a33 b3 a31 x1 a32 x2 .
(3.8)
Зададим некоторые начальные (нулевые) приближения значений
(0)
(0)
(0)
неизвестных: x1 x1 , x2 x2 , x3 x3 .
15.
Подставляя начальные приближения в правую часть 1-гоуравнения системы (3.8) получим новое приближение для x1:
1
x
b1 a12 x2(0) a13 x3(0) .
a11
(0)
Используя это значение для х1 и приближение x3 для х3, находим
из 2-го уравнения системы (3.8) первое приближение для х2:
1
(1)
x2
b2 a21 x1(1) a23 x3(0) .
a22
(1)
1
И, наконец, используя вычисленные значения x1 x1 и x2 x2 ,
находим с помощью 3-го уравнения системы (3.8) первое
приближение для х3:
(1)
(1)
3
x
1
b3 a31 x1(1) a32 x2(1) .
a33
На этом заканчивается первая итерация решения СЛУ (3.8).
(1)
16.
Критерий окончания итерационного процесса:k
k 1
max xi xi
1 i n
E,
где E – заданная допустимая погрешность.
Для сходимости итерационного процесса достаточно, чтобы модули
диагональных коэффициентов для каждого уравнения системы были не
меньше сумм модулей всех остальных коэффициентов, т. е.
aii aij , i 1, n.
i j
При этом хотя бы для одного уравнения неравенство должно
выполняться строго.
17. МЕТОД ПРОГОНКИ
• Если матрица системы является разреженной (ленточной врассматриваемом ниже примере), то есть содержит
большое число нулевых элементов, то применяют еще
одну модификацию метода Гаусса - метод прогонки.
• Рассмотрим систему уравнений с трех диагональной
матрицей.
18. Для решения данной системы по формулам прямого и обратного хода (прогонки), с использование программного пакета, необходимо
ввести обозначения. Обозначимматрицы коэффициентов при неизвестных (диагонально)
Рассмотрим решение системы. Дана система линейных
алгебраических уравнений (СЛАУ). Приведём её к виду, удобному
для реализации в прикладном пакете
19. . СР № 4. Прямые методы решения СЛАУ: метод Крамера, матричный метод, метод Гаусса
• Задание.• 1. Составить систему трёх уравнений с
тремя неизвестными.
• 2. решить заданную систему тремя
способами: метод Крамера, метод
Гаусса, матричный метод
• 3. Оформить все методы решения в
тетради (примеры см. ниже)
20. 3. Методы решения систем линейных уравнений
3.1. Метод с использованием обратной матрицыВ этом случае система записывается в матричном виде AX=B.
Тогда, умножая обе части этого векторного уравнения слева на
обратную матрицу A−1, получим X= A−1B. Для вычисления
обратной матрицы A−1 могут быть использованы разные методы,
например:
метод
алгебраических
дополнений
(через
алгебраические дополнения и определитель матрицы A); метод
Гаусса-Жордано; метод квадратных корней (для симметричной
матрицы A) и др. методы.
Метод непригоден для решения СЛУ при больших значениях n,
если не использовать экономичных схем для вычисления
матрицы A−1 , из-за большого объема вычислений.
21. 3.2. Метод исключения Гаусса и его модификации
Наиболее распространенным среди прямых методовявляется метод исключения Гаусса и его модификации.
Метод основан на приведении матрицы системы к
треугольному виду, что достигается путем последовательного
исключения неизвестных из уравнений системы.
Процесс решения СЛУ состоит из прямого хода метода
Гаусса и обратного хода метода Гаусса.
1) Алгоритм прямого хода метода Гаусса:
− с помощью первого уравнения исключается переменная x1 из всех
последующих уравнений системы;
− затем с помощью второго уравнения исключается x2 из третьего и всех
последующих уравнений;
− этот процесс продолжается до тех пор, пока в левой части последнего (nго) уравнения не останется лишь один член с неизвестным xn, т.е. матрица
системы будет приведена к треугольному виду. К такому виду можно
привести лишь невырожденную матрицу (иначе метод неприменим).
2) Алгоритм обратного хода метода Гаусса:
− решая последнее уравнение, находим единственное неизвестное xn;
− используя xn, найденное из предыдущего уравнения, находим xn−1 и т.д.;
− последним находится x1 из первого уравнения.
22. 3. Пример решения СЛУ
Рассмотрим применение метода Гаусса для системы третьего порядка:a11 x1 a12 x2 a13 x3 b1
a 21 x1 a 22 x2 a 23 x3 b2
a x a x a x b
31 1
32 2
33 3
3
(3.1)
Прямой ход. Для исключения x1 из второго уравнения прибавим к нему
первое, умноженное на – a21/a11. Аналогично, умножив первое на –
a31/a11 и прибавив к третьему, так же исключим x1 из третьего
уравнения.
Получим равносильную СЛУ вида
a11 x1 a12 x2 a13 x3 b1
x2 a23
x3 b2
a22
x2 a33
x3 b3
a32
ai1
a1 j (i, j=2,3); bi bi ai1 b1
где aij aij
a11
a11
(3.2)
(i=2,3).
23.
Теперь из третьего уравнения системы (3.2) нужно исключить x2. Дляэтого умножим второе уравнение на −a32'/a22' и прибавим результат к
третьему. Имеем:
a x a x a x b
где
a32
a33
;
a33
a23
a22
11 1
12 2
13 3
1
a22 x2 a23 x3 b2
a33 x3 b3
a32
b3 b3
b2 .
a22
(3.3)
Матрица системы (3.3) имеет треугольный вид. На этом заканчивается
прямой ход метода Гаусса. Необходимо заметить, что в процессе
исключения неизвестных приходится выполнять операции деления на
диагональные коэффициенты a11 , a22
и т.д. Поэтому они должны быть
отличны от «0». Иначе необходимо соответствующим образом
переставить уравнения системы.
Обратный ход. Обратный ход начинается с решения третьего уравнения:
x3=b3''/a33''. Используя полученное значение x3, можно найти х2 из
второго уравнения, а затем х1 из первого.
Аналогично строится вычислительный алгоритм для линейной системы
с произвольным числом n уравнений.
24. 4) Метод Гаусса с выбором главного элемента
Одной из модификаций метода Гаусса является схема с выборомглавного элемента. Она состоит в том, что требование
неравенства нулю диагональных элементов аkk, на которые
происходит деление в процессе исключения, заменяется более
жестким: из всех оставшихся в k-м столбце элементов нужно
выбрать наибольший по модулю элемент, и переставить
уравнения так, чтобы этот элемент оказался на месте аkk.
Диагональные элементы называются ведущими элементами:
ведущий элемент аkk − это коэффициент при k-м неизвестном в
k-м уравнении на k-м шаге исключения. Благодаря выбору
наибольшего по модулю ведущего элемента, уменьшаются
множители, используемые для преобразования уравнений.
Метод Гаусса с выбором главного элемента обеспечивает
приемлемую точность решения для сравнительно не большого
числа (n≤100) уравнений. Для плохо обусловленных систем
решения полученные по этому методу не надежны. Его
целесообразно использовать для решения СЛУ с плотно
заполненной матрицей. Все элементы матрицы и правые части
СУ находятся в ОЗУ.
25. Решите систему методом Крамера:
Решение:2 x1 3 x2 x3 9,
x1 2 x2 x3 3,
x 2 x 2.
3
1
1. Вычислим определитель системы:
2 3 1
1 2 1 2 2 2 3 1 1 1 1 0 1 2 1 3 1 2 2 1 0 13.
1 0 2
Так как определитель системы отличен от нуля, то система имеет единственное решение,
которое может быть найдено методом Крамера.
2. Составим и вычислим необходимые определители :
9
3 1
x1 3 2
1 9 2 2 3 1 2 1 3 0 1 2 2 3 3 2 9 1 0 52,
2
0
2
2
9 1
x2 1
3
1 2 3 2 9 1 1 1 1 2 1 3 1 9 1 2 2 1 2 0,
1
2
2
3
9
2
x3 1 2
1
0
3 2 2 2 3 3 1 9 1 0 9 2 1 3 1 2 2 3 0 13.
2
26. Решите систему методом Крамера:
2 x1 3 x2 x3 9,x1 2 x2 x3 3,
x 2 x 2.
3
1
3. Находим неизвестные по формулам Крамера:
x1
x1
x1
x2
x3
, x2
x1
x2
x3
x2
, x3
x3
52
4,
13
0
0,
13
13
1.
13
Ответ:
x1 4, x2 0, x3 1.
;
27. Решите систему методом Гаусса:
2 x1 3 x2 x3 9,x1 2 x2 x3 3,
x 2 x 2.
3
1
Решение:
1. Первое уравнение оставим без изменения, а из 2-го и 3-го исключим слагаемые, содержащие x1.
Для этого второе уравнение умножим на
, а затем сложим с 1-ым уравнением.
a11
2
a 21
Аналогично третье уравнение умножим на
, а затем сложим с первым.
В результате исходная система примет вид: a11 2
a31
2 x1 3 x2 x3 9,
7 x2 3 x3 3,
2. Теперь из последнего уравнения исключим
слагаемое, содержащее x2. Для этого третье
3 xсо2 вторым.
5 x3 5Тогда
.
уравнение умножим на
, и сложим
будем иметь систему уравнений:
a22
7
a32
3
2 x1 3 x2 x3 9,
7 x2 3 x3 3,
2
2
8 x3 8 .
3
3
28. Решите систему методом Гаусса:
2 x1 3 x2 x3 9,x1 2 x2 x3 3,
x 2 x 2.
3
1
3. На этом прямой ход метода Гаусса закончен, начинаем обратный ход.
Из последнего уравнения полученной системы уравнений находим x3:
2
3 1.
x3
2
8
3
8
Из второго уравнения получаем:
x2
1
3 3x3 1 3 3 1 0 .
7
7
Из первого уравнения находим оставшуюся неизвестную переменную и этим завершаем
обратный ход метода Гаусса:
Ответ:
x1
x1 4, x2 0, x3 1.
1
9 3x2 x3 1 9 3 0 1 4 .
2
2
29. Решите систему матричным методом:
2 x1 3 x2 x3 9,x1 2 x2 x3 3,
x 2 x 2.
3
1
Решение:
1. Перепишем систему уравнений в матричной форме:
A X B
Так как
2 3 1
2 3 1 x1 9
1
2
1
x2 3 .
1 0
2 x3 2
1 2 1 2 2 2 3 1 1 1 1 0 1 2 1 3 1 2 2 1 0 13 ,
1
0 2
то систему трёх линейных уравнений с тремя неизвестными можно решить матричным
методом. С помощью обратной матрицы решение этой системы может быть найдено
как:
1
X A 1 B
x1 2 3 1 9
x 1 2 1 3 .
2
x 1 0 2 2
3
30. Решите систему матричным методом:
2. Построим обратную матрицуэлементов матрицы A :
A11 A12 A13
1
1
A A21 A22 A23
A
A31 A32 A33
где
A11 1
1 1
3 1
T
2 1
4, A12 1
3 1
2
A 1 с помощью матрицы из алгебраических дополнений
6
1
4
T
13
13
13
1
4 1 2
4 6
1
1
1
5
3
6
5 3 1
5 3
,
13
13
13 13 13
1 3 7
2 3 7 2
3
7
13 13 13
1 2
0 2
2 1 3 1
A21 1
6,
0 2
A31 1
2 x1 3 x2 x3 9,
x1 2 x2 x3 3,
x 2 x 2.
3
1
1
1,
1 1
1, A13 1
1 3
1 2
2 2 2 1
A22 1
1 2
A32 1
3 2
5,
2 1
1
1
1 2
2,
1 0
2 3 2 3
A23 1
3,
1 0
3, A33 1 3 3
2 3
1 2
7.
31. Решите систему матричным методом:
2 x1 3 x2 x3 9,x1 2 x2 x3 3,
x 2 x 2.
3
1
3. Осталось вычислить матрицу неизвестных переменных, умножив обратную матрицу
на матрицу-столбец свободных членов:
4
6
1
6
1
4
9 3 2
13
13
13 13 9 13
13
4
1
5
3
1
3
5
1
X A B
9 3 2 0 ,
3
13 13
13
13
13 13
2
1
2
3
7
2 9 3 3 7 2
13
13 13 13
13
13
x1 4
X x2 0 .
Ответ:
. x 1
3
x1 4, x2 0, x3 1
32.
2 x1 x2x 4x
1
2
3 x1 2 x2
2 x1 4 x2
4 x3 3 x4 4
3 x3 2 x4 1
2 x3
x4 3
2 x3
3 x4 6
2 4 4
x 2
2
3
1
1
3
2
3
3
2
1
2
6
2 3
x3
1
1 4
4
3
3
2
1
4
x1
1 4
3
3
2
1
2
2
6
4
2 3
2
1
4 4
2
2
2
4
2 3
2
1
4
3
1
4
1
2
3
2
3
1
3
2
4
6
3
2
x 4
4
3
3
Ответ: (1; 2; 2; 0)
1
1 4
3
1
2
2
3
4
2
6
33.
2 x1 x2x 4x
1
2
3 x1 2 x2
2 x1 4 x2
x1
x1
4 x3 3 x4 4
3 x3
2 x4 1
2 x3
x4 3
2 x3
3 x4 6
4 x2
3 x3
2 x4
1
x2
10
x3
9
7
x4
9
41x3
35 x 4
82
16 x3
25 x 4
32
x1
x
2
x3
x 4
2
9
x1
4 x2
3 x3
2 x4
1
14 x 2 11x3
7 x4
6
12 x 2
8 x3
x4
8
9 x2
10 x3
7 x4
2
4 x2
3 x3
2 x4
x2
10
x3
9
7
x4
9
25
x4
16
x3
1
2
2
0
Ответ: (1; 2; 2; 0)
x4
1
2
9
2
0
34.
2 x1 x2x 4x
1
2
3 x1 2 x2
2 x1 4 x2
4 x3 3 x4 4
3 x3
2 x4 1
2 x3
x4 3
2 x3
3 x4 6
1
1
2
2
3
2
0
9
10
7
0
0
82
70
0
0
16
25
2
2
164
32
1
1
2
2
0
0
9
10
0
0
0
1
0
0
0
0
1
4
4 3 2 1
2 2 1
3
4 2 3 6
2
4
1
1
3
2
3
1
1
2
2
3
2
2
0
9
10
7
2
0
0
41
35
82
0
0
0
265
0
2
2
2
0
1
1
2
0
0
0
9
0
0
0
0
1
0
0
0
0
1
2
18
2
0
Ответ: (1; 2; 2; 0)
1
0
0
0
1
2
9
2
2
0
1
8
7
0
3
1
2
2
6
1
0
1
5
3
2
7
2
2
3
2
0
9
10
7
0
0
41
0
0
0
0
1
0 0 0 1
1 0 0 2
0 1 0 2
0 0 1 0
2
1
18
10
2
2
82
0

































 Математика
Математика








