Похожие презентации:
Системы линейных уравнений и методы их решения. (Тема 2)
1. Системы линейных уравнений
и методы их решения2. План изложения темы
1. Основные сведения о СЛУ:Определение
Виды
Разрешимость
2. Методы решения СЛУ:
Метод обратной матрицы
Метод Крамера
Метод Гаусса
Метод Жордана-Гаусса
3. Понятие СЛОУ
3. Литература
Высшая математика для экономистов:Учебник для студентов вузов. Под ред.
проф. Н.Ш. Кремера.
Высшая математика для экономистов:
Практикум для студентов вузов. Под
ред. проф. Н.Ш. Кремера.
4. Система линейных уравнений (СЛУ)
из m уравнений с n неизвестнымиимеет вид:
a11 x1 a12 x 2 a13 x3 ... a1n x n b1 ;
a x a x a x ... a x b ;
21 1
22 2
23 3
2n n
2
...
a m1 x1 a m 2 x 2 a m 3 x3 ... a mn x n bm .
где
aij-коэффициенты при переменных;
bi
- свободные члены уравнений
5. Краткая форма записи СЛУ
С помощью знаков суммированиясистему записывают в виде:
n
aij x j bi ,
j 1
i 1, m
6. Матричная форма СЛУ
Обозначения:b1
b2
В
...
b
m
вектор
свободных
членов
СЛУ принимает вид матричного уравнения:
а11 а12 ... а1n
x1
x2
a 21 a 22 ... a 2 n
А
X
... ... ... ...
...
a
a
...
a
x
m3
m1 m 2
n
основная матрица
вектор
системы
неизвестных
А Х В
7. Решение СЛУ
Решением СЛУ называетсяупорядоченный набор (вектор) значений
X x1 , x2 , x3 ,...xn , при подстановке
которого в СЛУ, каждое уравнение
обращается в верное равенство.
Решить СЛУ – найти множество всех его
решений.
8. Равносильные СЛУ
Две системы уравнений называютсяравносильными или эквивалентными,
если они имеют одно и то же множество
решений.
Элементарные преобразования над
матрицей приводят к получению систем,
равносильных данной.
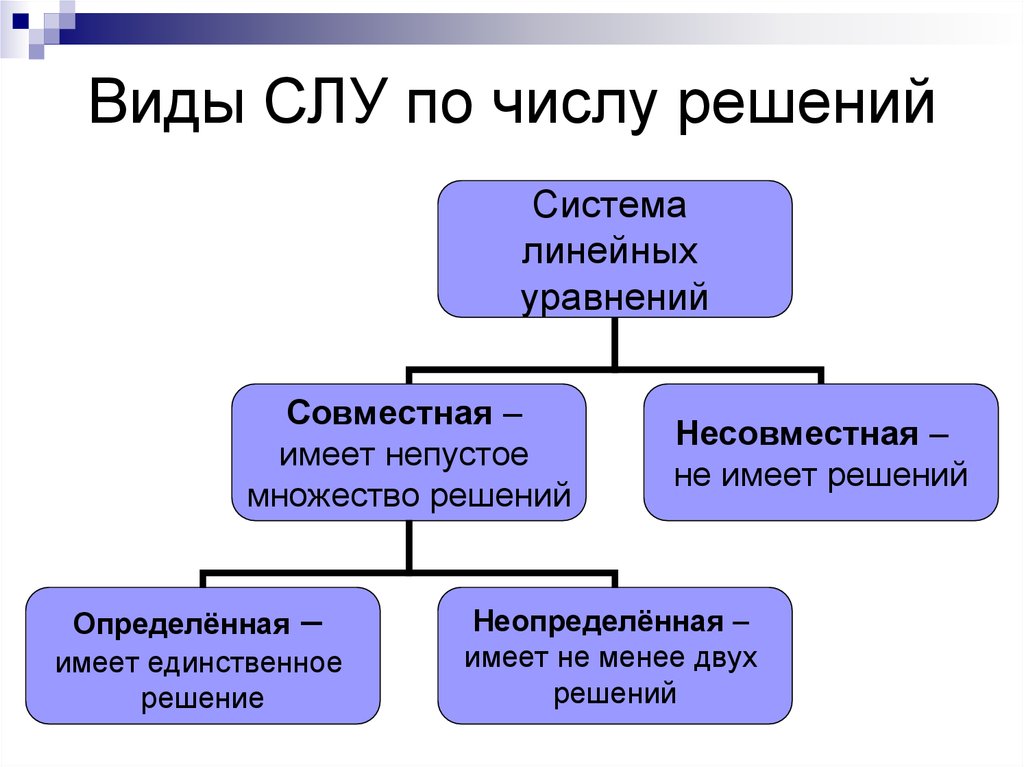
9. Виды СЛУ по числу решений
Системалинейных
уравнений
Совместная –
имеет непустое
множество решений
Определённая –
имеет единственное
решение
Несовместная –
не имеет решений
Неопределённая –
имеет не менее двух
решений
10. Разрешимость СЛУ
Расширенной матрицей системы называетсяматрица (А|В).
Теорема Кронекера-Капелли: СЛУ совместна
тогда и только тогда, когда ранг основной
матрицы системы равен рангу ее расширенной
матрицы, т.е. СЛУ совместна ↔ r(A) = r(A|B).
Совместная система имеет
единственное решение (определённа), если
ранг расширенной матрицы равен числу
неизвестных;
бесконечное число решений (неопределённа),
если ранг меньше числа неизвестных.
11. Система n уравнений с n неизвестными (СЛУ n×n)
Число уравнений равно числунеизвестных (m=n).
Основная матрица системы А является
квадратной.
Определитель det А = ∆А называется
определителем системы.
12. Методы решения СЛУ
Метод обратной матрицы – для СЛУ n×n;Метод Крамера - для СЛУ n×n;
Метод Гаусса – для всех СЛУ;
Метод Жордана-Гаусса – для всех СЛУ.
13. Метод обратной матрицы
Для СЛУ n×n,А Х В
o записанной в матричном виде
o имеющей невырожденную матрицу А (∆А ≠ 0)
имеется единственное решение Х, определяемое
формулой:
o
1
X A B
Если ∆А =0, то метод обратной матрицы
неприменим для решения СЛУ.
Применяется не только в решении СЛУ, но и
других матричных уравнений.
14. Метод Крамера
Обозначим ∆ - определитель системы,∆i – определитель, получаемый заменой в
матрице А j-го столбца на столбец свободных
членов В.
При ∆≠0 СЛУ совместна определённа, её
единственное решение находят по формулам
xj
j
,
j 1, n
Если ∆=0 и хотя бы один ∆i ≠0, то система
несовместна (не имеет решений).
Если ∆=0 и все ∆i =0, то система совместна
неопределённа, её решения находят другими
методами.
15. Метод Гаусса
1.2.
является универсальным, т.е. применим для
решения любой СЛУ.
Др. название – метод последовательного
исключения неизвестных.
Идея метода – заменить СЛУ более простой
равносильной системой.
Осуществляется в 2 этапа:
«Прямой ход» - преобразование расширенной
матрицы системы к ступенчатому виду с
помощью элементарных преобразований;
«Обратный ход» - решение равносильной
системы, начиная с последнего уравнения.
16. Базисное решение СЛУ
Пусть r(A)=r и r<n. Выберем r переменныхx1 , x2 ,..., xr
таких, что определитель из коэффициентов при
них (базисный минор) отличен от нуля.
Такие переменные назовём основными или
базисными.
Остальные n-r переменных называют
неосновными или свободными.
Решение СЛУ, в котором все свободные
переменные равны нулю, называют базисным.
Число базисных решений СЛУ конечно и не
превосходит С r
n















 Математика
Математика








