Похожие презентации:
Пирамида. Решение задач по теме «Пирамида». 10 класс
1.
УРОК-ПРАКТИКУМВ 10 КЛАССЕ
Пирамида. Решение
задач по теме
«Пирамида».
2.
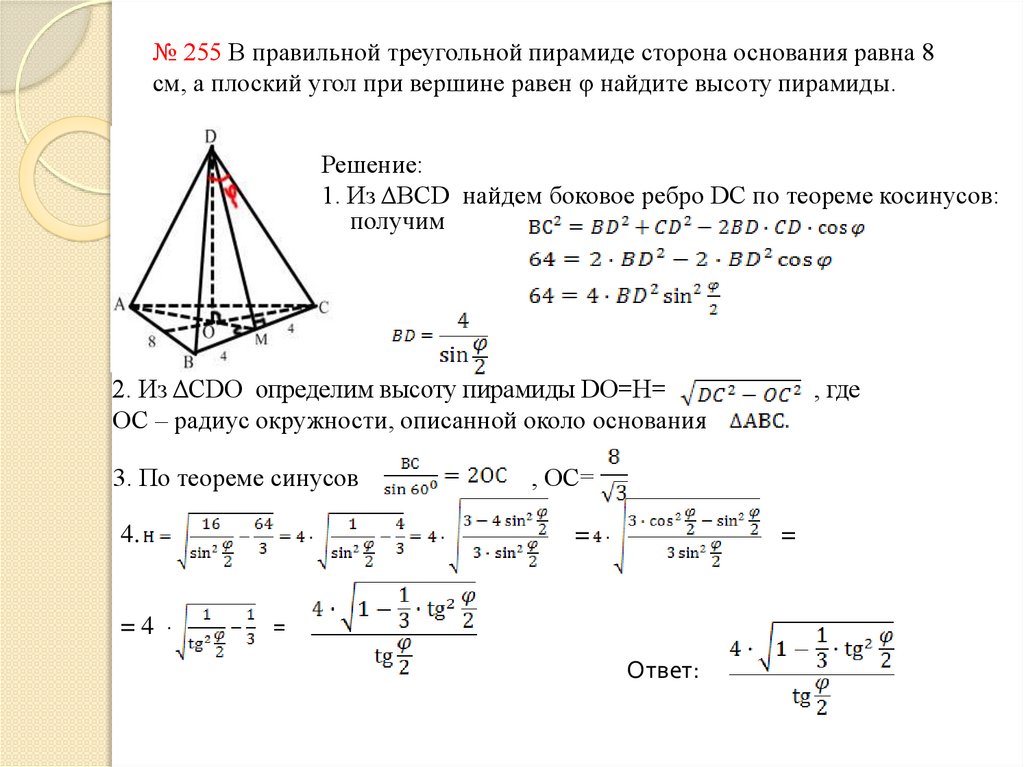
№ 255 В правильной треугольной пирамиде сторона основания равна 8см, а плоский угол при вершине равен φ найдите высоту пирамиды.
Решение:
1. Из ΔBCD найдем боковое ребро DC по теореме косинусов:
получим
2. Из ΔCDO определим высоту пирамиды DO=H=
ОС – радиус окружности, описанной около основания
3. По теореме синусов
4.
=4
, где
, ОС=
=
=
=
Ответ:
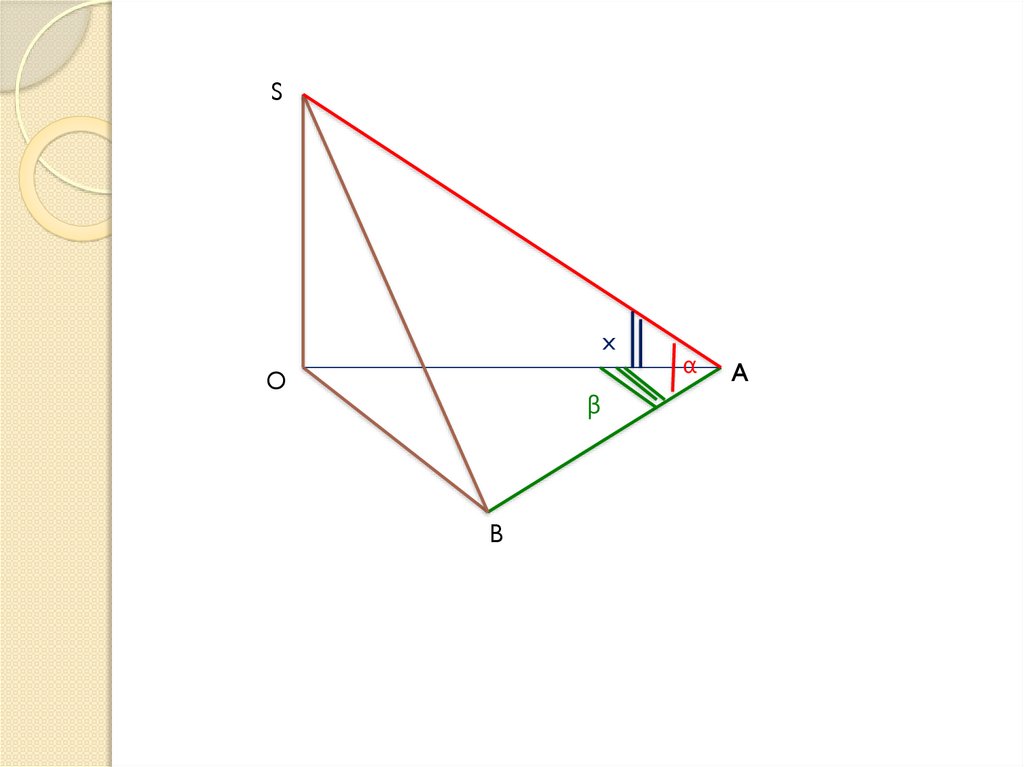
3.
Sx
O
β
B
α
A
4.
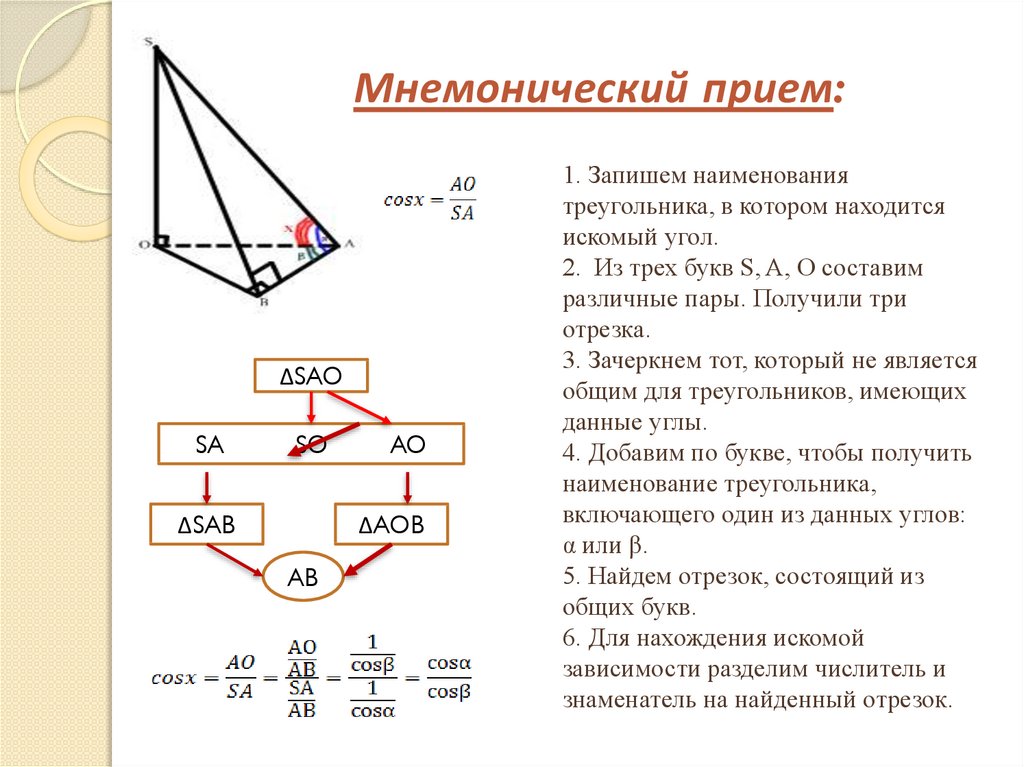
Мнемонический прием:ΔSAO
SA
SO
ΔSAB
AO
ΔAOB
AB
1. Запишем наименования
треугольника, в котором находится
искомый угол.
2. Из трех букв S, A, O составим
различные пары. Получили три
отрезка.
3. Зачеркнем тот, который не является
общим для треугольников, имеющих
данные углы.
4. Добавим по букве, чтобы получить
наименование треугольника,
включающего один из данных углов:
α или β.
5. Найдем отрезок, состоящий из
общих букв.
6. Для нахождения искомой
зависимости разделим числитель и
знаменатель на найденный отрезок.
5.
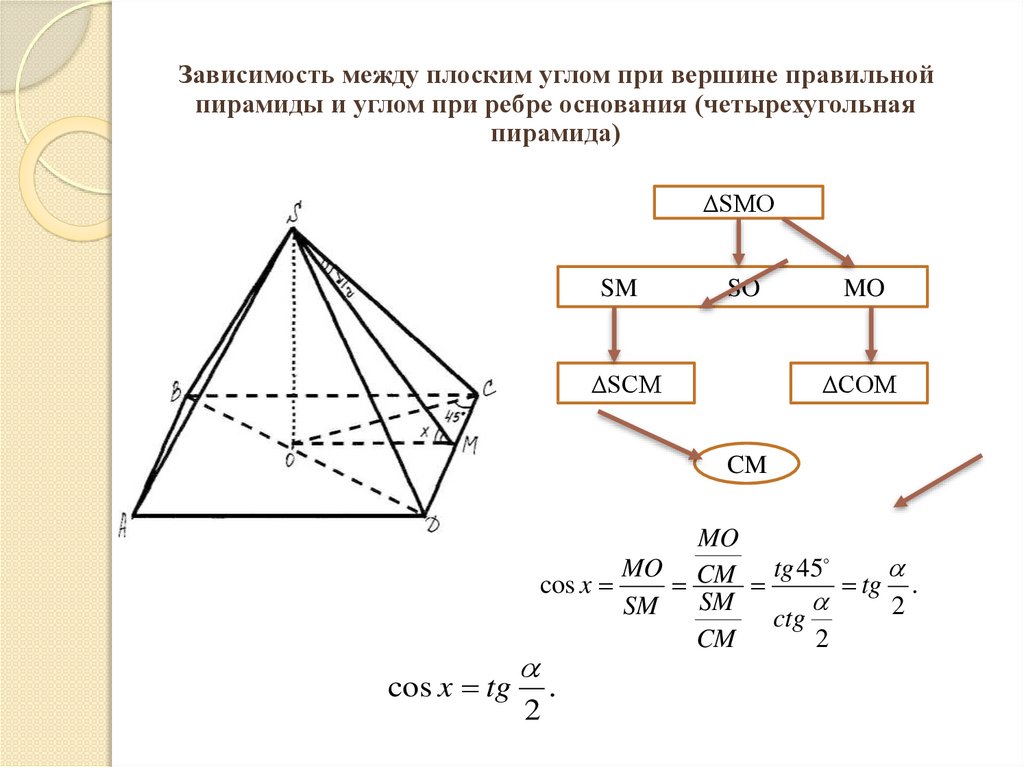
Зависимость между плоским углом при вершине правильнойпирамиды и углом при ребре основания (четырехугольная
пирамида)
ΔSMO
SM
SO
ΔSCM
MO
ΔCOM
CM
cos x tg
MO
MO CM tg 45
cos x
tg .
SM
SM
2
ctg
CM
2
2
.
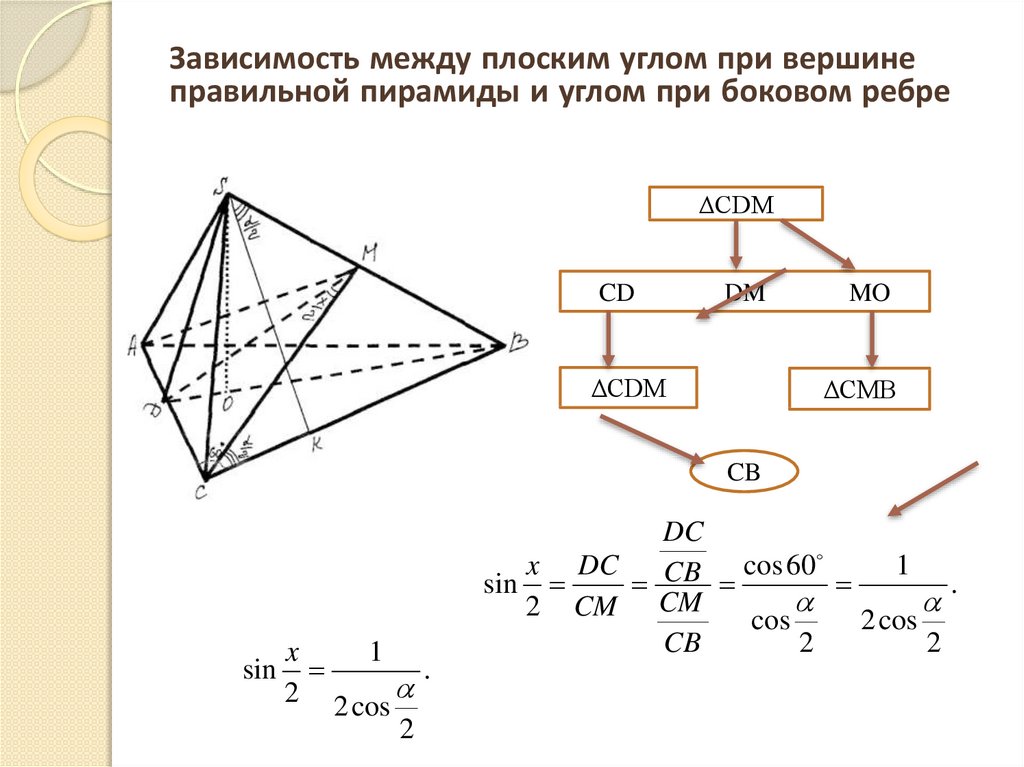
6.
Зависимость между плоским углом при вершинеправильной пирамиды и углом при боковом ребре
ΔCDM
CD
DM
ΔCDM
MO
ΔCMB
CB
x
1
sin
.
2 2 cos
2
DC
x DC
cos
60
1
CB
sin
.
CM
2 CM
cos
2 cos
CB
2
2
7.
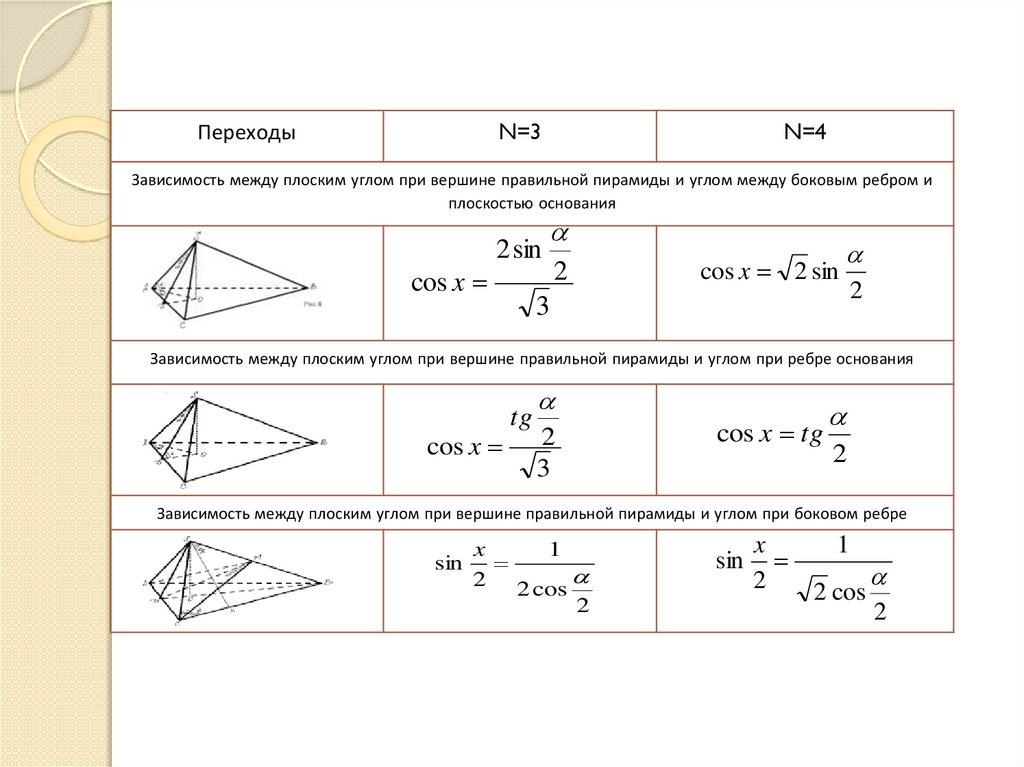
N=3Переходы
N=4
Зависимость между плоским углом при вершине правильной пирамиды и углом между боковым ребром и
плоскостью основания
cos x
2 sin
2
cos x 2 sin
3
2
Зависимость между плоским углом при вершине правильной пирамиды и углом при ребре основания
cos x
tg
2
3
cos x tg
2
Зависимость между плоским углом при вершине правильной пирамиды и углом при боковом ребре
sin
x
1
2 2 cos
2
sin
x
2
1
2 cos
2
8.
Вернемся к задаче 255В правильной треугольной пирамиде сторона основания равна 8 см, а
плоский угол при вершине равен φ найдите высоту пирамиды.
1. Из ΔАВС найдем
.
2. Применим формулу перехода для ∟DMO=X:
, отсюда
3. По теореме Пифагора DO=
=
Ответ:
.
.
=4
=
9.
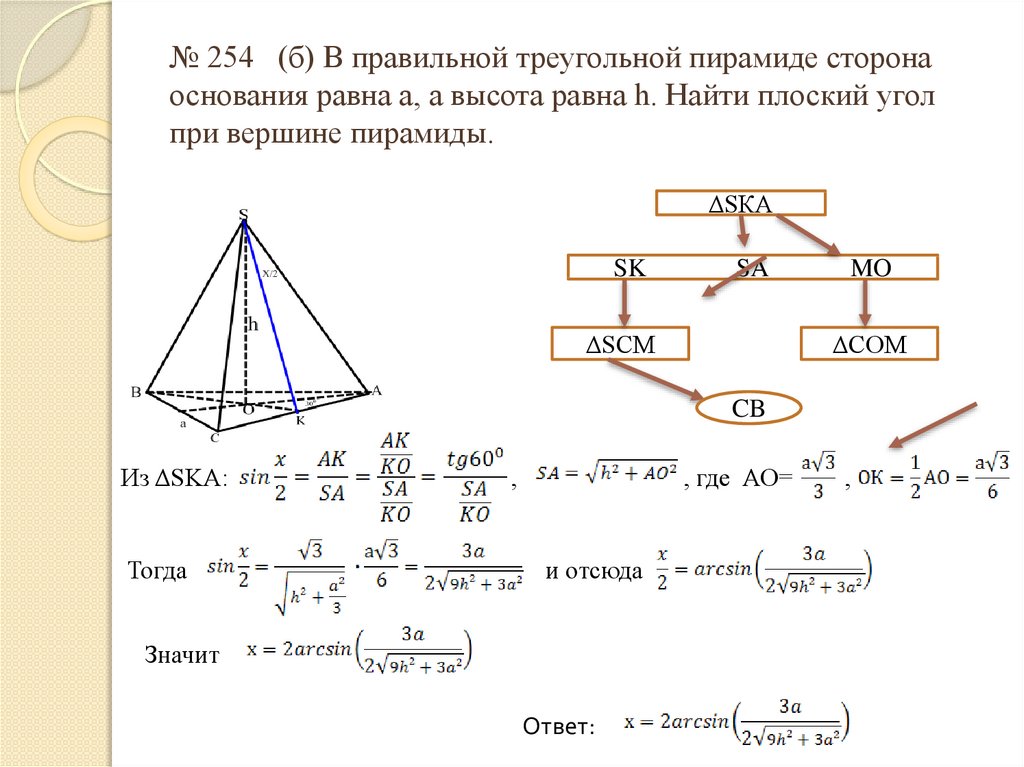
№ 254 (б) В правильной треугольной пирамиде сторонаоснования равна а, а высота равна h. Найти плоский угол
при вершине пирамиды.
ΔSКА
SK
SA
ΔSCM
MO
ΔCOM
CB
Из ΔSKA:
Тогда
,
, где АО=
и отсюда
Значит
Ответ:
,


 Математика
Математика








