Основы проектирования схем автоматики

1.

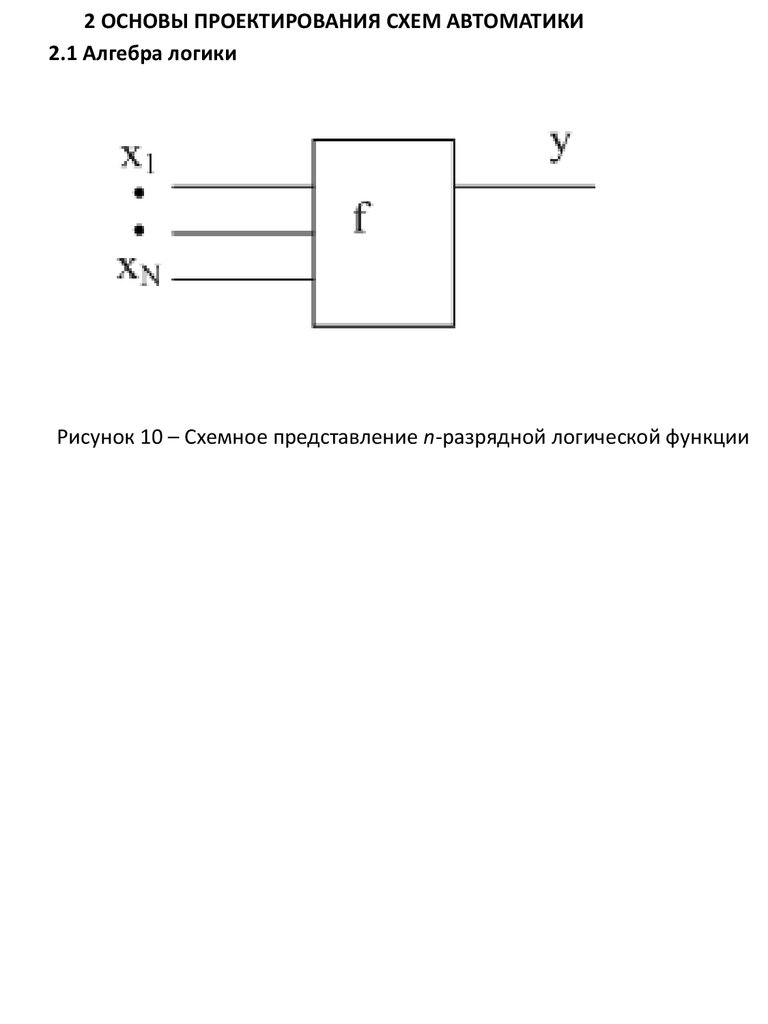
2 ОСНОВЫ ПРОЕКТИРОВАНИЯ СХЕМ АВТОМАТИКИ
2.1 Алгебра логики
Рисунок 10 – Схемное представление n-разрядной логической функции

2.

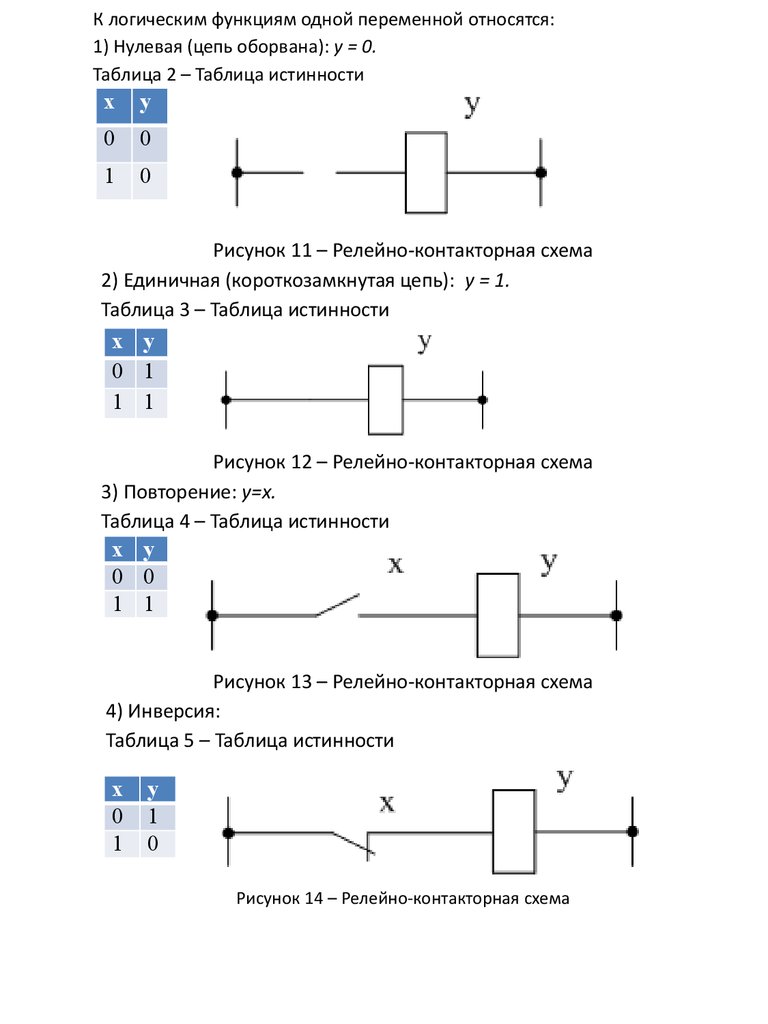
К логическим функциям одной переменной относятся:
1) Нулевая (цепь оборвана): у = 0.
Таблица 2 – Таблица истинности
х
у
0
0
1
0
Рисунок 11 – Релейно-контакторная схема
2) Единичная (короткозамкнутая цепь): у = 1.
Таблица 3 – Таблица истинности
х у
0 1
1 1
Рисунок 12 – Релейно-контакторная схема
3) Повторение: у=х.
Таблица 4 – Таблица истинности
х у
0 0
1 1
Рисунок 13 – Релейно-контакторная схема
4) Инверсия:
Таблица 5 – Таблица истинности
х
0
1
у
1
0
Рисунок 14 – Релейно-контакторная схема

3.

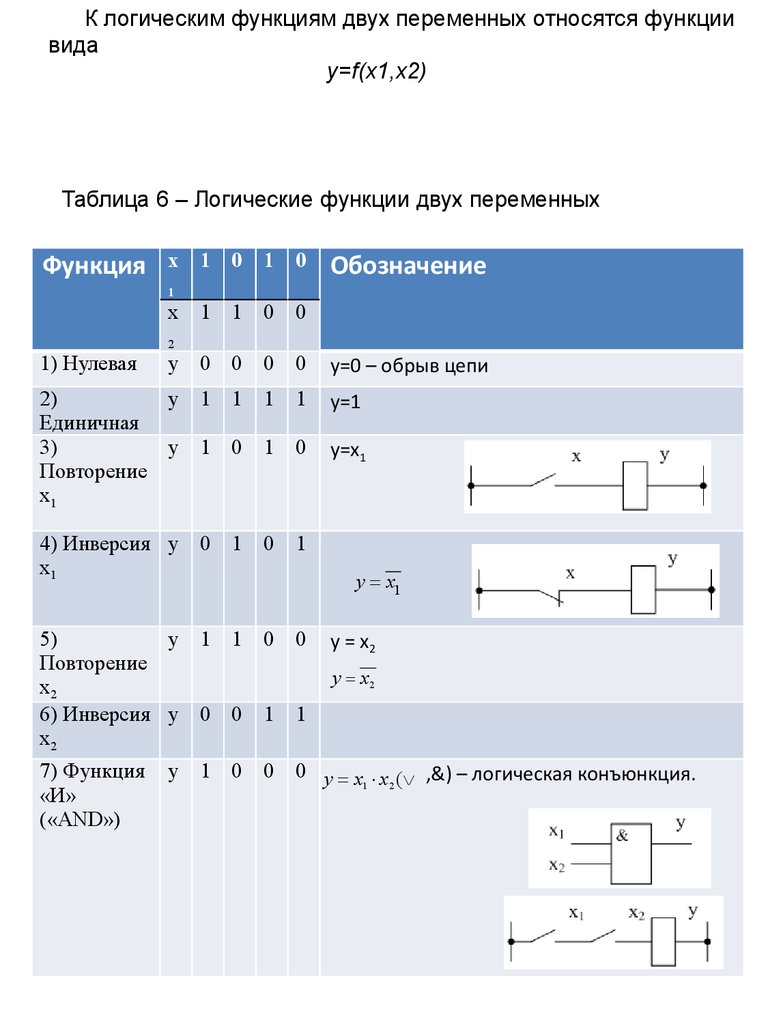
К логическим функциям двух переменных относятся функции
вида
у=f(x1,x2)
Таблица 6 – Логические функции двух переменных
Функция
х
Обозначение
1
0 1
0
1
1 0
0
у
0
0 0
0
у=0 – обрыв цепи
2)
у
Единичная
3)
у
Повторение
х1
1
1 1
1
у=1
1
0 1
0
у=х1
4) Инверсия у
х1
0
1 0
1
5)
у
Повторение
х2
6) Инверсия у
х2
1
0
0 1
1
7) Функция
«И»
(«AND»)
1
0 0
0 y x х ( ,&) – логическая конъюнкция.
1
2
1
х
2
1) Нулевая
у
y х1
1 0
0
у = х2
y х2

4.

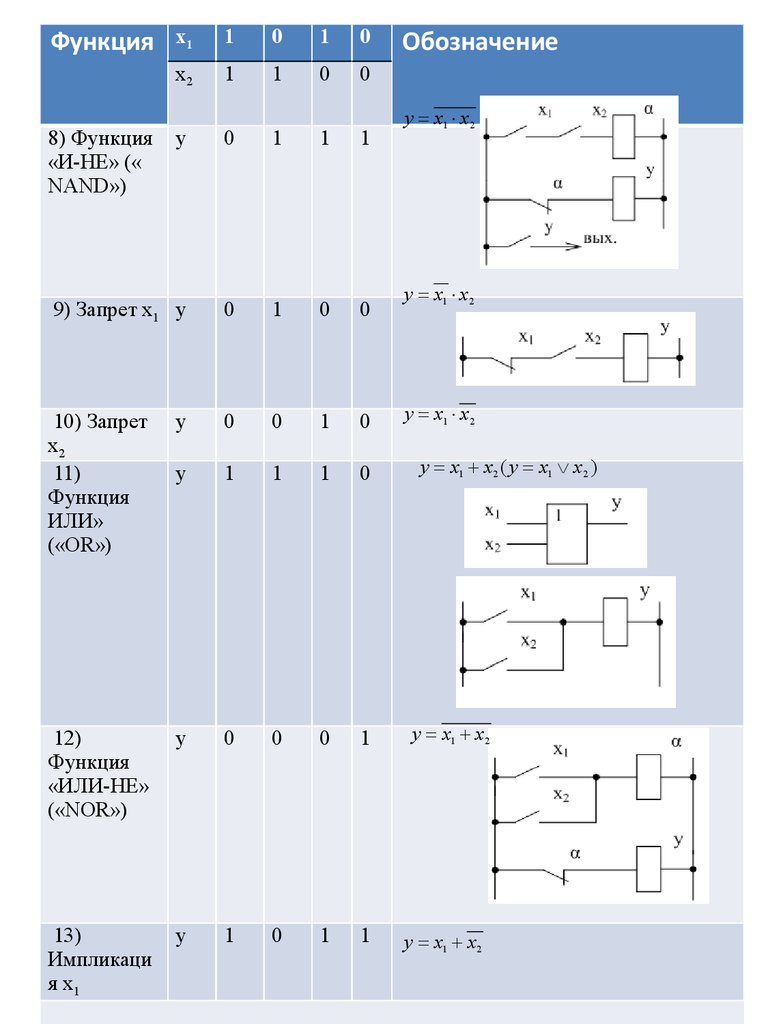
Функция
8) Функция
«И-НЕ» («
NAND»)
х1
1
0
1
0
х2
1
1
0
0
у
0
1
1
1
9) Запрет х1 у
0
1
0
0
10) Запрет
х2
11)
Функция
ИЛИ»
(«OR»)
у
0
0
1
0
у
1
1
1
0
12)
Функция
«ИЛИ-НЕ»
(«NOR»)
у
0
0
0
1
13)
Импликаци
я х1
у
1
0
1
1
Обозначение
y х1 х2
y х1 х2
y х1 х2
y х1 х2 ( у х1 х2 )
y х1 х2
y х1 х2

5.

Функция
Обозначение
х1
1
0
1
0
х2
1
1
0
0
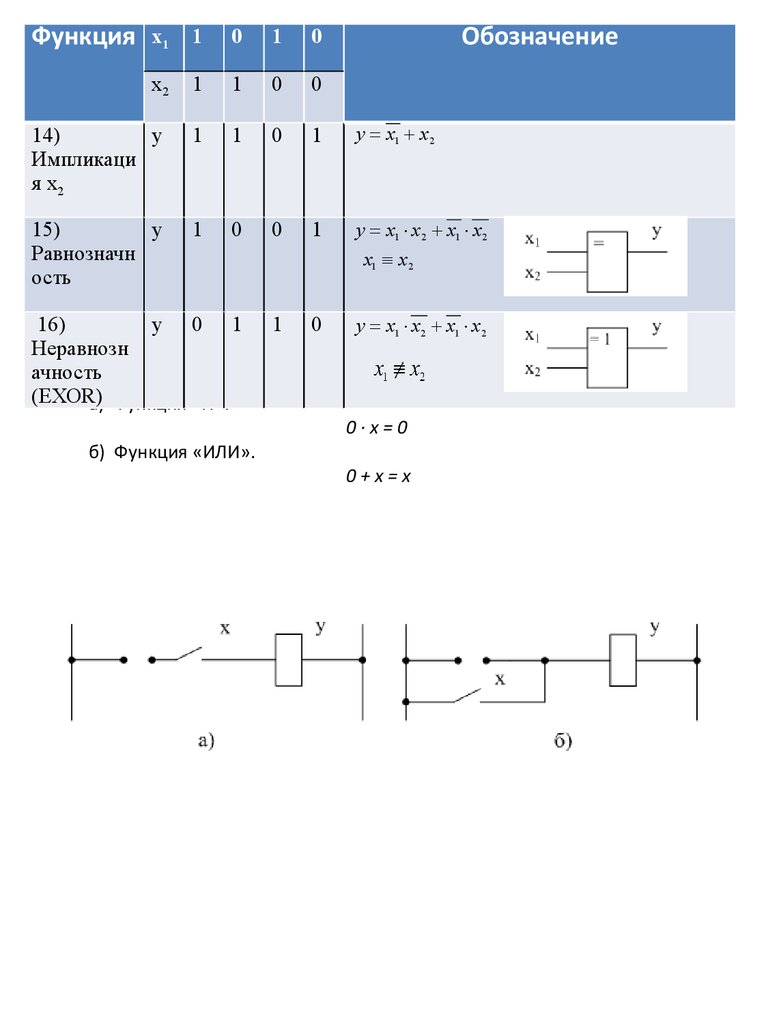
14)
у
Импликаци
я х2
1
1
0
1
y х1 х2
15)
у
Равнозначн
ость
1
0
0
1
y x1 х2 х1 х2
х1 х2
16)
у 0 1 1 0
y x1 х2 х1 х2
Неравнозн
2.2 Основные законы алгебры логики
ачность
Закон нулевого множества.
(ЕХОR)
а) Функция «И».
0·х=0
б) Функция «ИЛИ».
0+х=х
Рисунок 15 – Релейно-контакторные схемы
2) Закон универсального множества.
а) Функция «И».
1·х=х

6.

б) Функция «ИЛИ».
1+х=1
Рисунок 16 – Релейно-контакторная схема
3) Закон двойной инверсии.
х х
Рисунок 17 – Релейно-контакторная схема
4) Закон повторения.
а) Функция «И».
х·х=х
б) Функция «ИЛИ».
х+х=х
Рисунок 18 – Релейно-контакторные схемы
5) Распределительный закон.
Рисунок 19 – Релейно-контакторные схемы
х1 ( х2 х3 ) х1 х2 х1 х3

7.

6. Закон поглощения.
х1 ( х1 х2 ) х1 ,
х1. х1 х1 х2 х1 х1 х2 х1 (1 х2 ) х1
7. Закон склеивания.
х1 х2 х1 х2 х1 ,
( х1 хи2 нормальные
) ( х1 х2 ) х1 формы записи
2.3 Синтез таблицы истинности
Пример – Требуется синтезировать схему, предотвращающую пуск двигателя при
определенных условиях.
А = 1 – дверь закрыта;
А = 0 – дверь открыта;
В = 1 – перегрузка;
В = 0 – нет перегрузки;
С = 1 – кнопка нажата;
С = 0 – кнопка не нажата.
Таблица 7 – Таблица истинности
А
0
0
0
0
1
1
1
1
В
0
0
1
1
0
0
1
1
С
0
1
0
1
0
1
0
1
у
0
0
0
0
0
1
0
0

8.

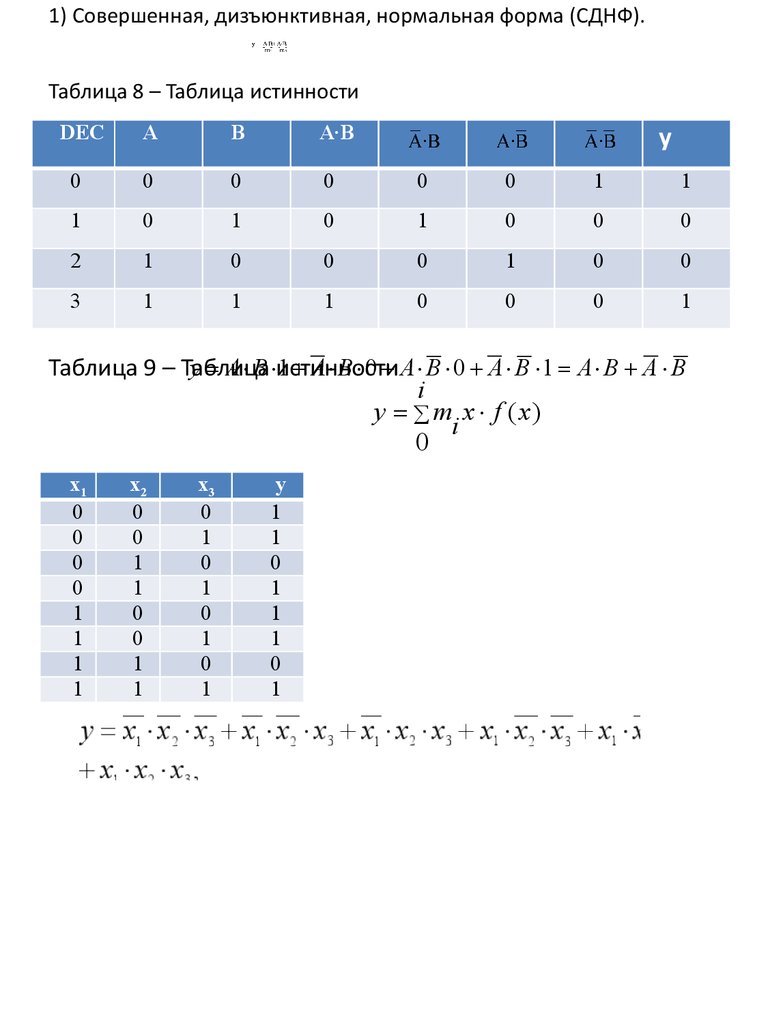
1) Совершенная, дизъюнктивная, нормальная форма (СДНФ).
Таблица 8 – Таблица истинности
DEC
у
А
В
А∙В
0
0
0
0
0
0
1
1
1
0
1
0
1
0
0
0
2
1
0
0
0
1
0
0
3
1
1
1
0
0
0
1
Таблица 9 – Таблица
у А В истинности
1 А В 0 А В 0 А В 1 А В А В
i
у m х f ( x)
i
0
х1
0
0
0
0
1
1
1
1
х2
0
0
1
1
0
0
1
1
х3
0
1
0
1
0
1
0
1
у
1
1
0
1
1
1
0
1

9.

2) Совершенная, конъюнктивная, нормальная форма (СКНФ).
у ( А В) ( А В )
М0
М3
у ( А В 0) ( А В 1) ( А В 1) ( А В 0) ( А В) ( А В )
Таблица 10 – Таблица истинности
А
В
0
0
0
1
1 – СКНФ.
0
Пример
1
1
у
0
1
1
0
DEC
0
1
2
3
Таблица 11 – Таблица истинности
х1
0
0
0
0
1
1
1
1
х2
0
0
1
1
0
0
1
1
х3
0
1
0
1
0
1
М20
1
у
1
1
0
1
1
1
0 М6
1
у ( х1 х2 х3 ) ( х1 х2 х3 )

10.

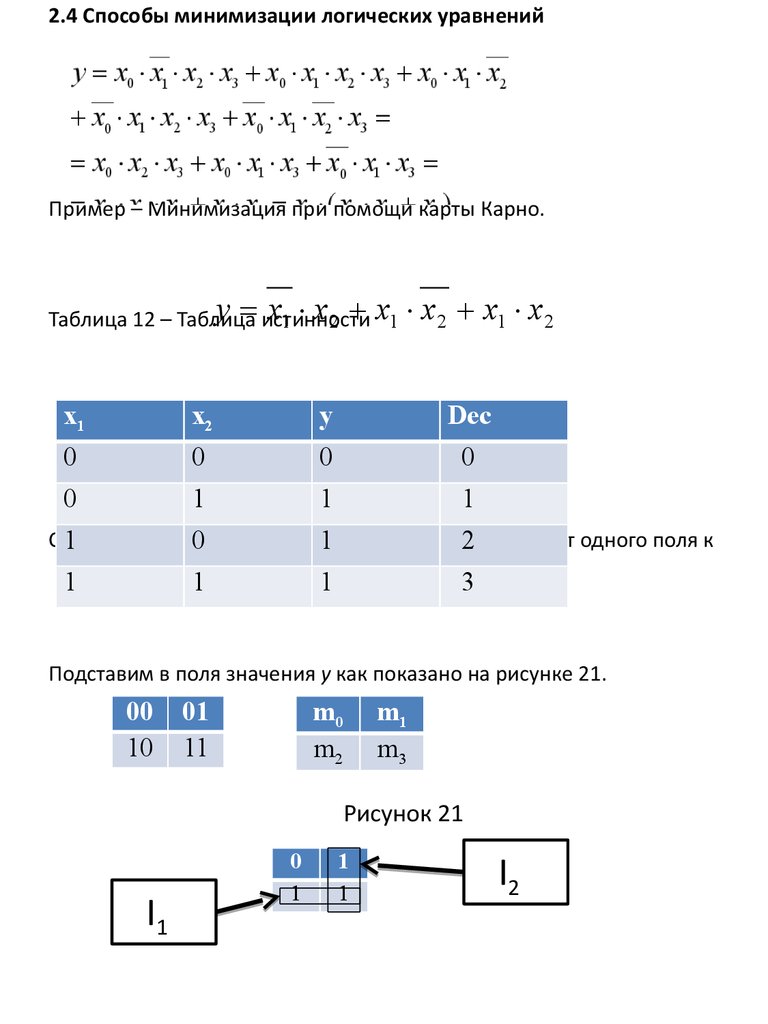
2.4 Способы минимизации логических уравнений
Пример – Минимизация при помощи карты Карно.
у истинности
х1 х 2 х1
Таблица 12 – Таблица
х 2 х1 х 2
х1
х2
у
Dec
0
0
0
0
0
1
1
1
Сконструируем
от одного поля к
1
0диаграмму так,
1 чтобы при переходе
2
другому изменялась только одна переменная.
1
1
1
3
Подставим в поля значения у как показано на рисунке 21.
00
10
01
11
m0
m2
m1
m3
Рисунок 21
I1
0
1
1
1
I2

11.

I1 m2 m3 х1 х2 х1 х2 x1
I 2 m1 m3 х1 х2 х1 х 2 x2
y I 1 I 2 x1 x2
Карта Карно для трех переменных:
у х1 х 2 х3 х1 х 2 х3 х1 х 2 х3 х1 х2 х3
х 2 х3
х 2 х3
х 2 х3
х1
х1
х 2 х3
1
1
1
1
I
Необходимо убрать те переменные, которые в зоне
импликанта меняют свое значение.
у=х2.
Этот метод работает, когда в каждое слагаемое входят все
переменные.
Пример – Построение карты Карно для трех переменных.
у х1 х2 х3 х1 х3 х1 х3 х2 х1 х2

12.

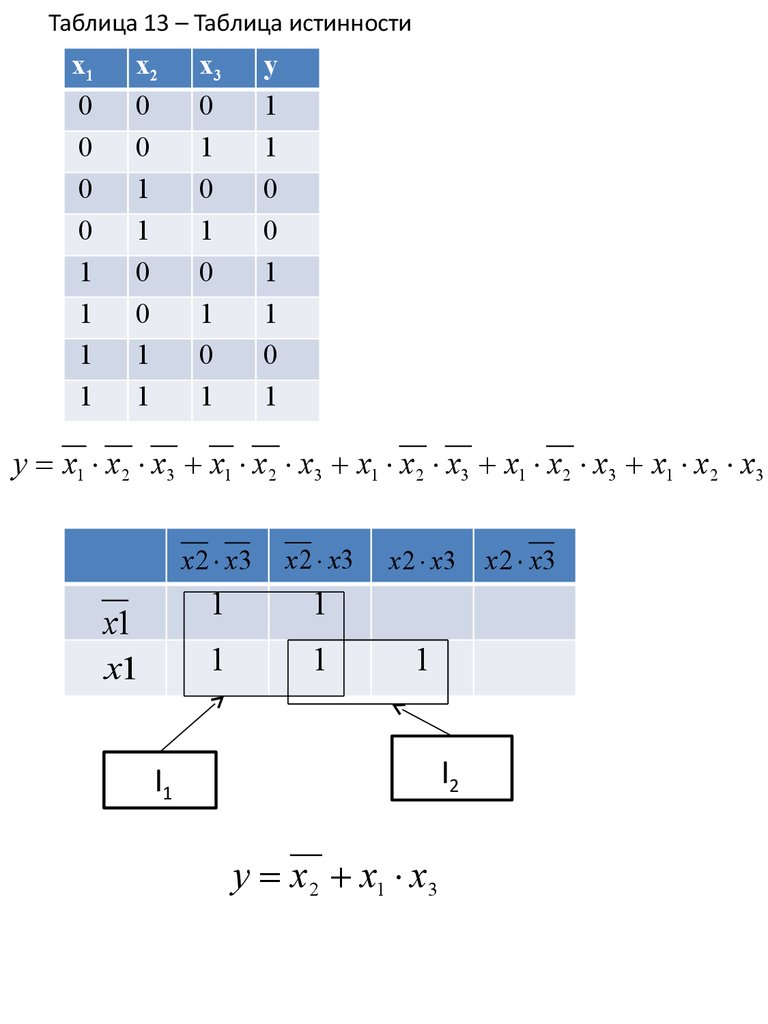
Таблица 13 – Таблица истинности
х1
0
0
0
0
1
1
1
1
х2
0
0
1
1
0
0
1
1
х3
0
1
0
1
0
1
0
1
у
1
1
0
0
1
1
0
1
у х1 х2 х3 х1 х2 х3 х1 х2 х3 х1 х2 х3 х1 х2 х3
х1
х1
х 2 х3
х 2 х3
1
1
1
1
х 2 х3
1
I2
I1
у х2 х1 х3
х 2 х3

13.

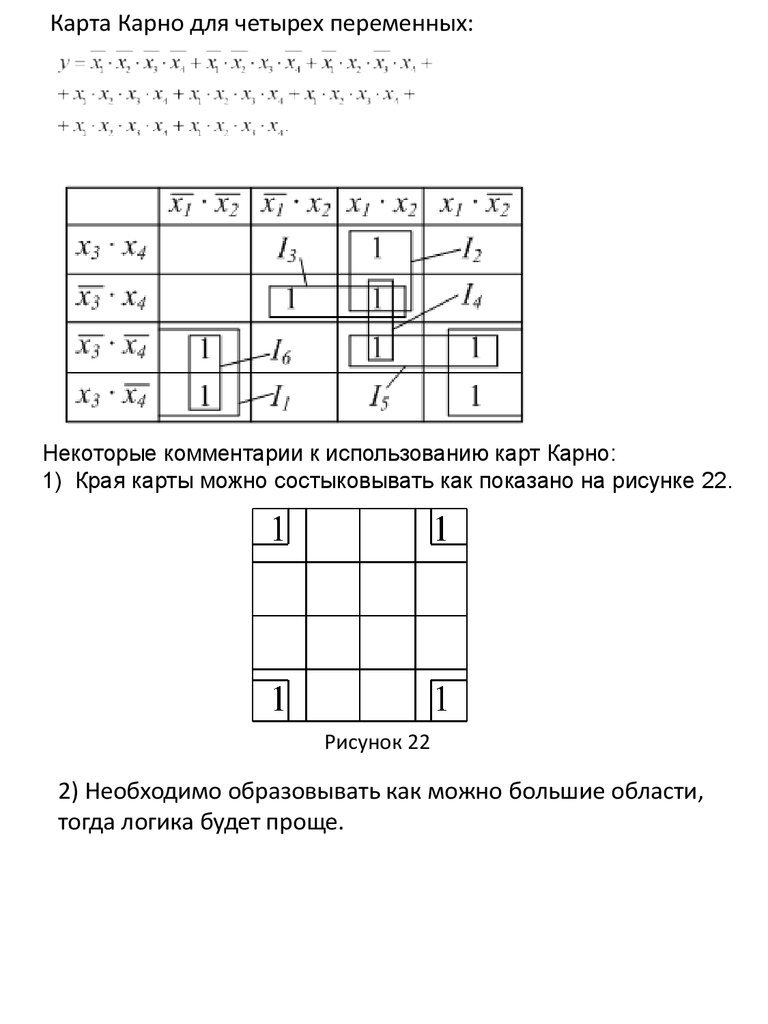
Карта Карно для четырех переменных:
Некоторые комментарии к использованию карт Карно:
1) Края карты можно состыковывать как показано на рисунке 22.
Рисунок 22
2) Необходимо образовывать как можно большие области,
тогда логика будет проще.

14.

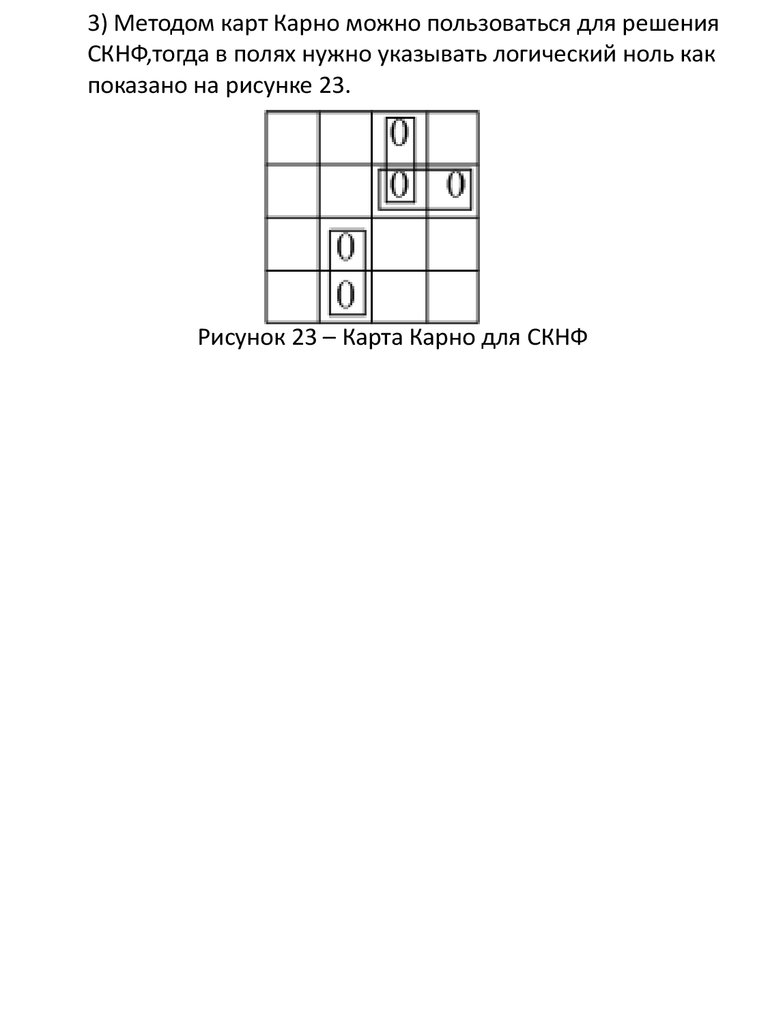
3) Методом карт Карно можно пользоваться для решения
СКНФ,тогда в полях нужно указывать логический ноль как
показано на рисунке 23.
Рисунок 23 – Карта Карно для СКНФ

15.

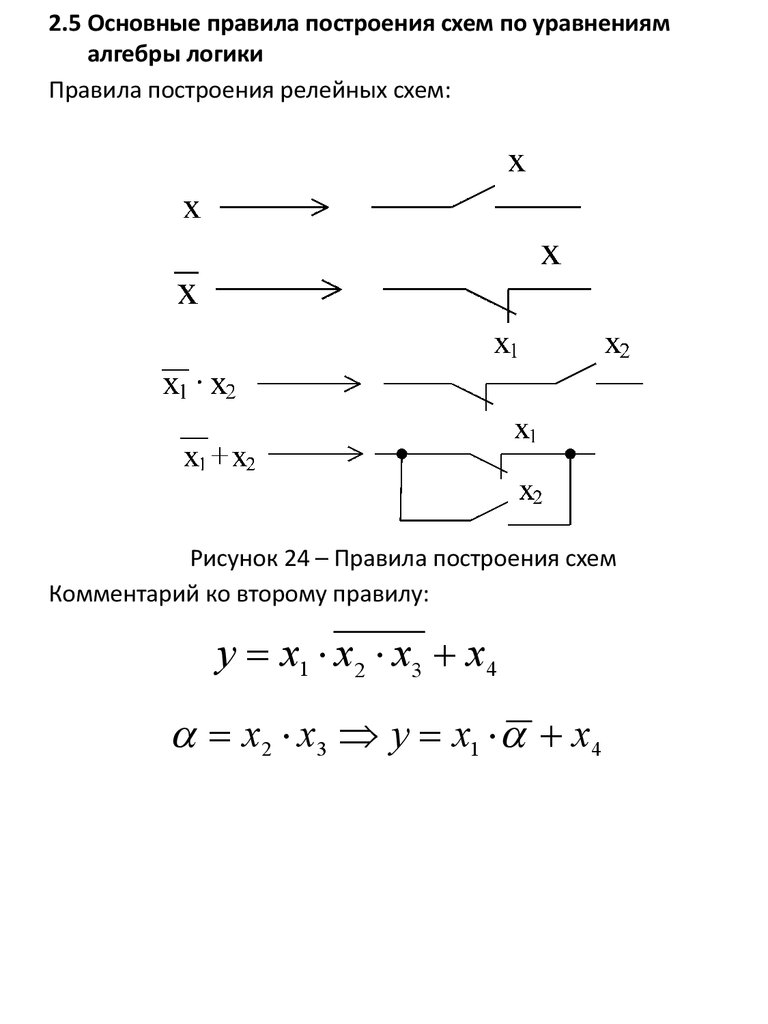
2.5 Основные правила построения схем по уравнениям
алгебры логики
Правила построения релейных схем:
Рисунок 24 – Правила построения схем
Комментарий ко второму правилу:
у х1 х2 х3 х4
х2 х3 у х1 х4

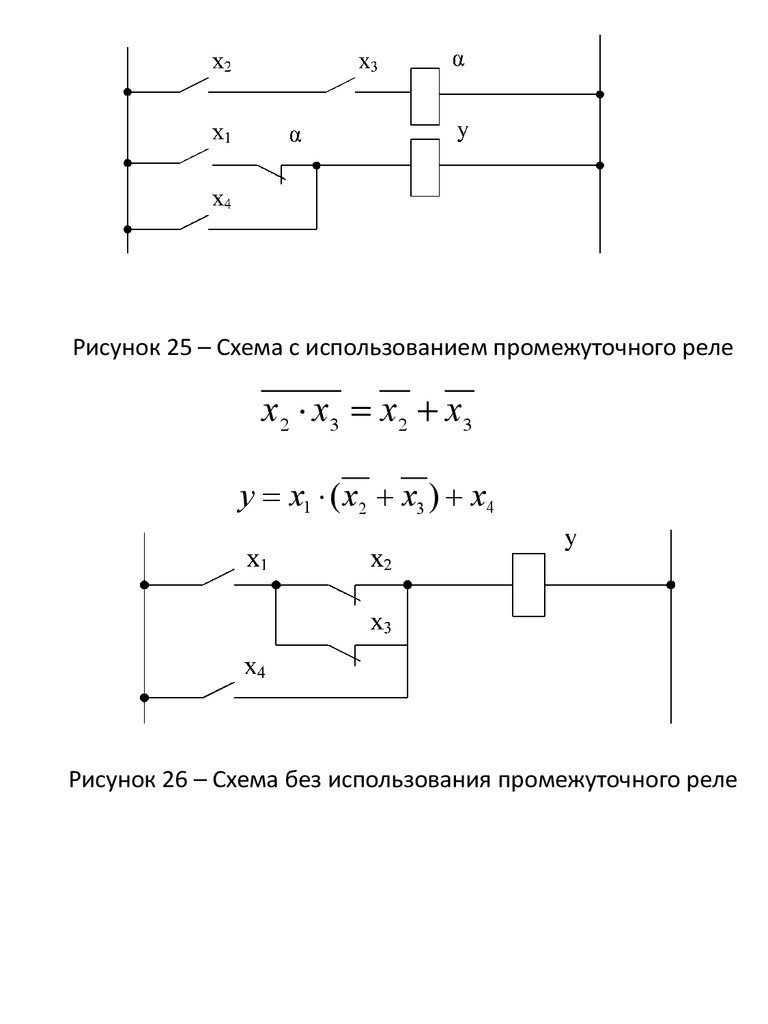
16.

Рисунок 25 – Схема с использованием промежуточного реле
х 2 х3 х 2 х3
у х1 ( х2 х3 ) х4
Рисунок 26 – Схема без использования промежуточного реле

17.

Правила построения бесконтактных схем:
1) Исходное логическое уравнение необходимо привести к виду, состоящему
только из элементарных логических операций (“И”, “ИЛИ”, “НЕ”) и
минимизировать.
2) Очень часто управляющая схема должна быть построена на основе
элементарной базы одного типа (“И-НЕ”, “ИЛИ-НЕ”), тогда исходное
уравнение необходимо преобразовать в уравнение, содержащее только это
элемент.
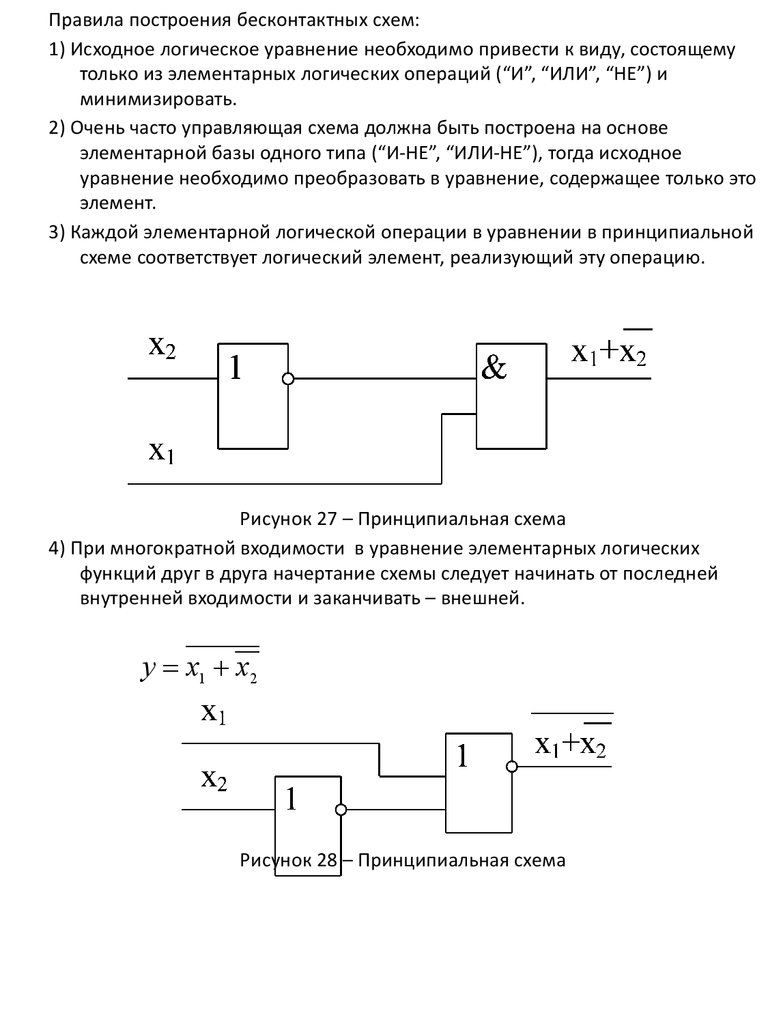
3) Каждой элементарной логической операции в уравнении в принципиальной
схеме соответствует логический элемент, реализующий эту операцию.
Рисунок 27 – Принципиальная схема
4) При многократной входимости в уравнение элементарных логических
функций друг в друга начертание схемы следует начинать от последней
внутренней входимости и заканчивать – внешней.
у х1 х2
Рисунок 28 – Принципиальная схема

18.

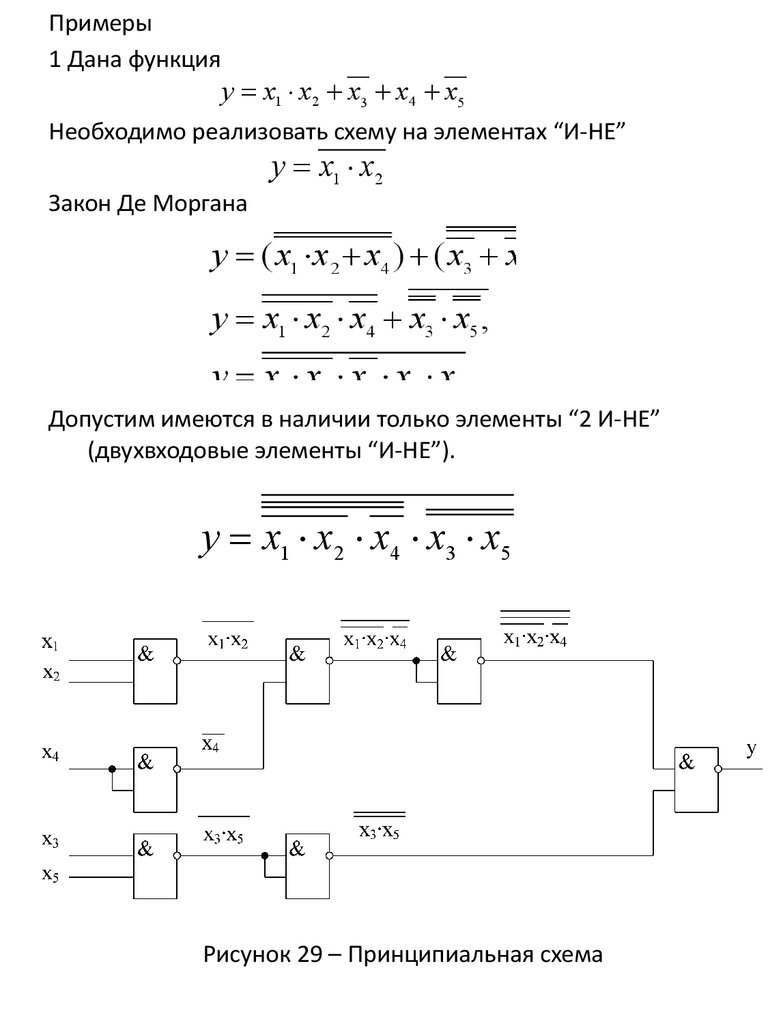
Примеры
1 Дана функция
у х1 х2 х3 х4 х5
Необходимо реализовать схему на элементах “И-НЕ”
Закон Де Моргана
у х1 х2
Допустим имеются в наличии только элементы “2 И-НЕ”
(двухвходовые элементы “И-НЕ”).
у х1 х2 х4 х3 х5
Рисунок 29 – Принципиальная схема

19.

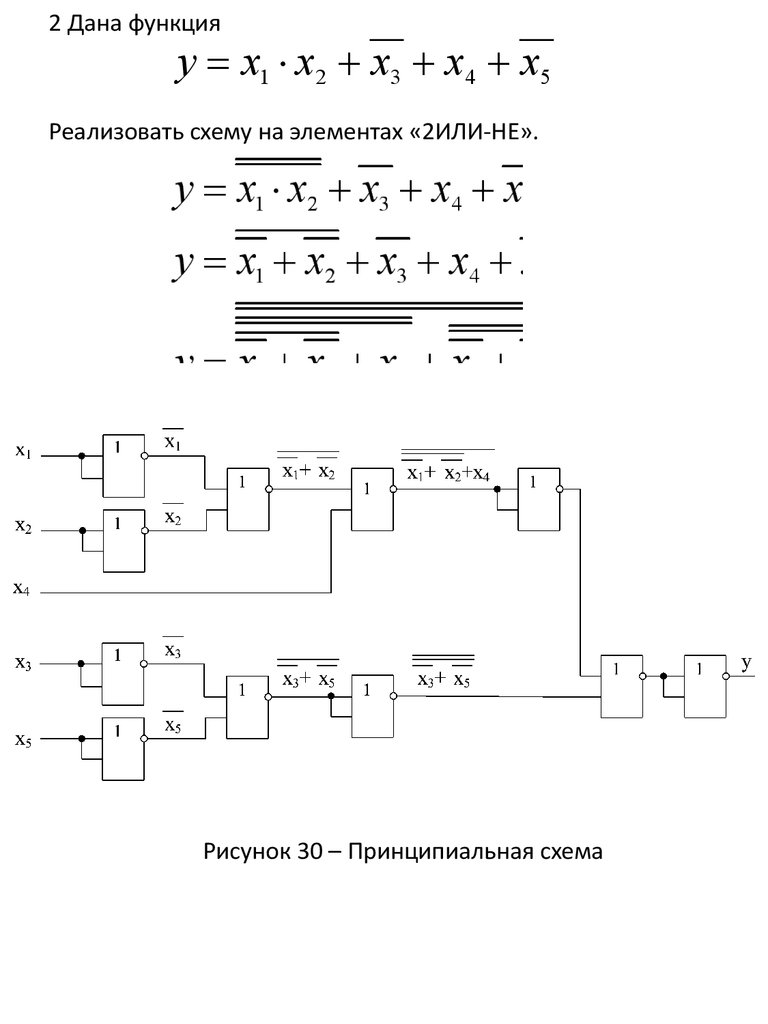
2 Дана функция
у х1 х2 х3 х4 х5
Реализовать схему на элементах «2ИЛИ-НЕ».
Рисунок 30 – Принципиальная схема

20.

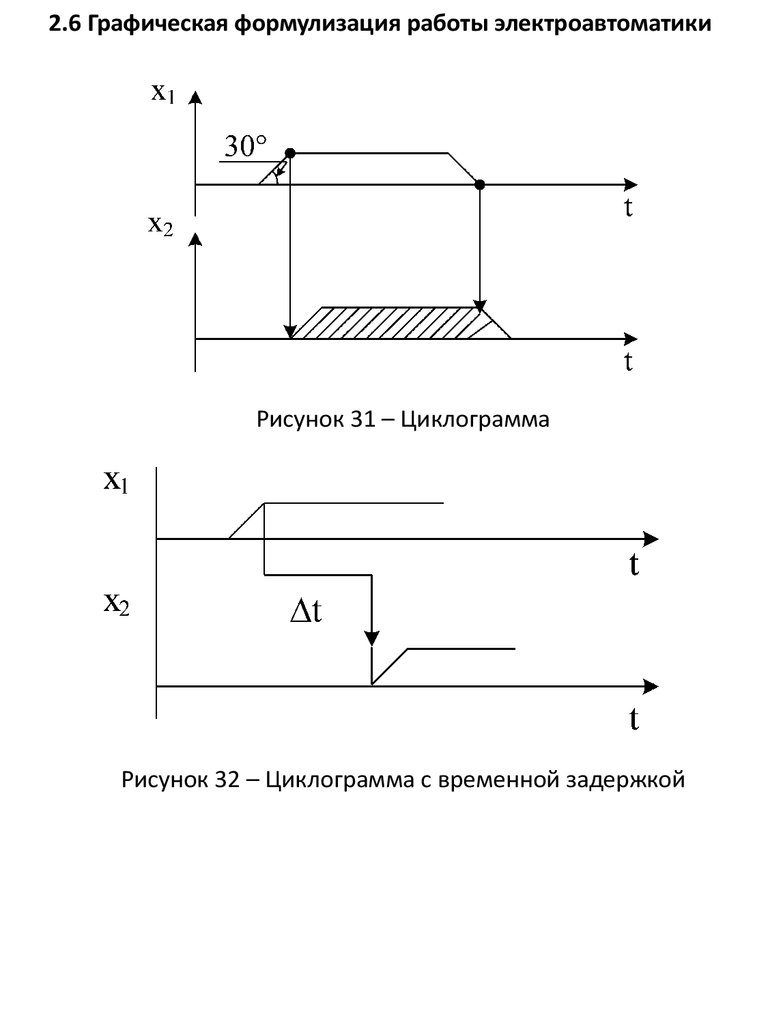
2.6 Графическая формулизация работы электроавтоматики
Рисунок 31 – Циклограмма
Рисунок 32 – Циклограмма с временной задержкой

21.

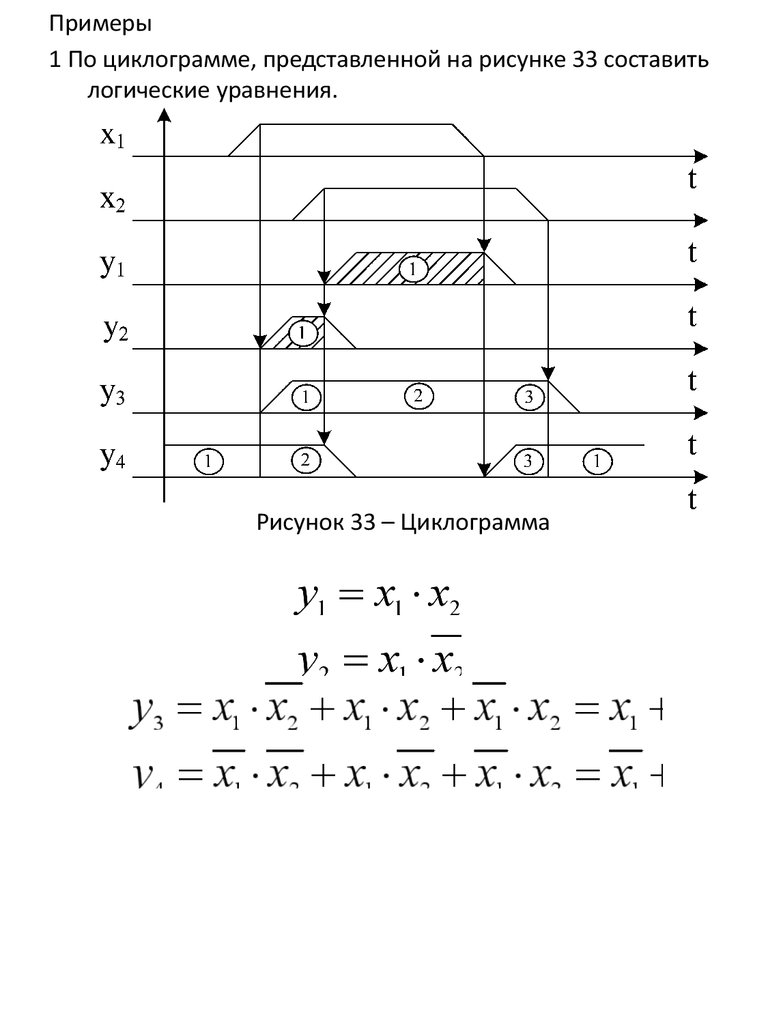
Примеры
1 По циклограмме, представленной на рисунке 33 составить
логические уравнения.
Рисунок 33 – Циклограмма

22.

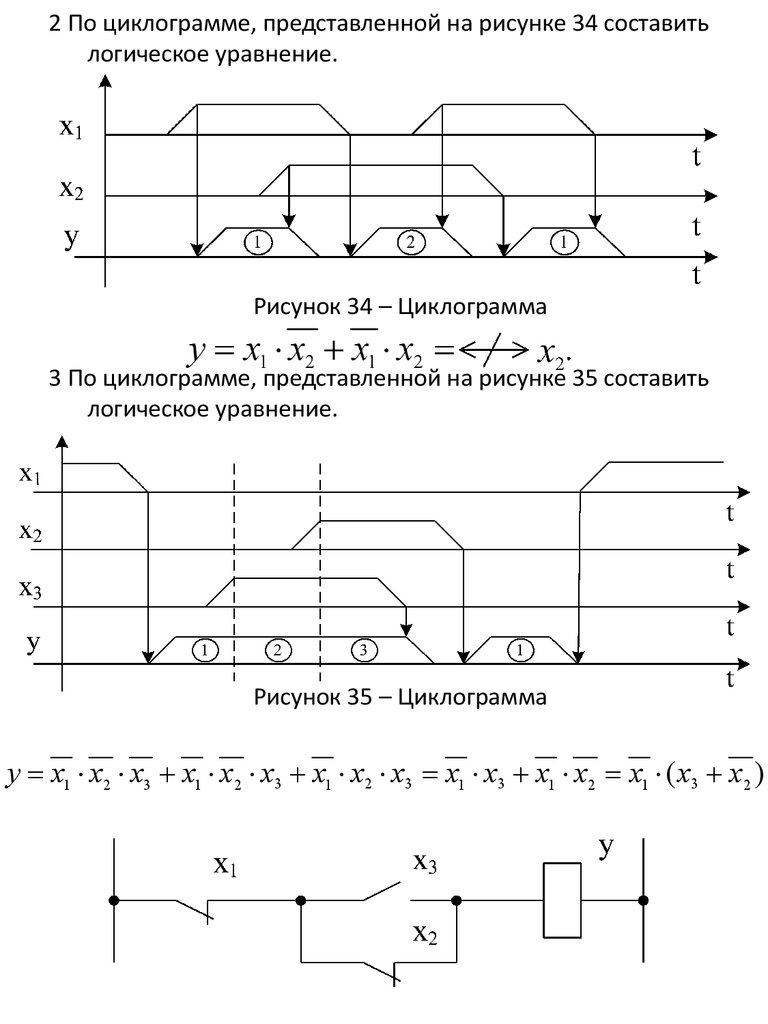
2 По циклограмме, представленной на рисунке 34 составить
логическое уравнение.
Рисунок 34 – Циклограмма
3 По циклограмме, представленной на рисунке 35 составить
логическое уравнение.
Рисунок 35 – Циклограмма
у х1 х2 х3 х1 х2 х3 х1 х2 х3 х1 х3 х1 х2 х1 ( х3 х2 )

23.

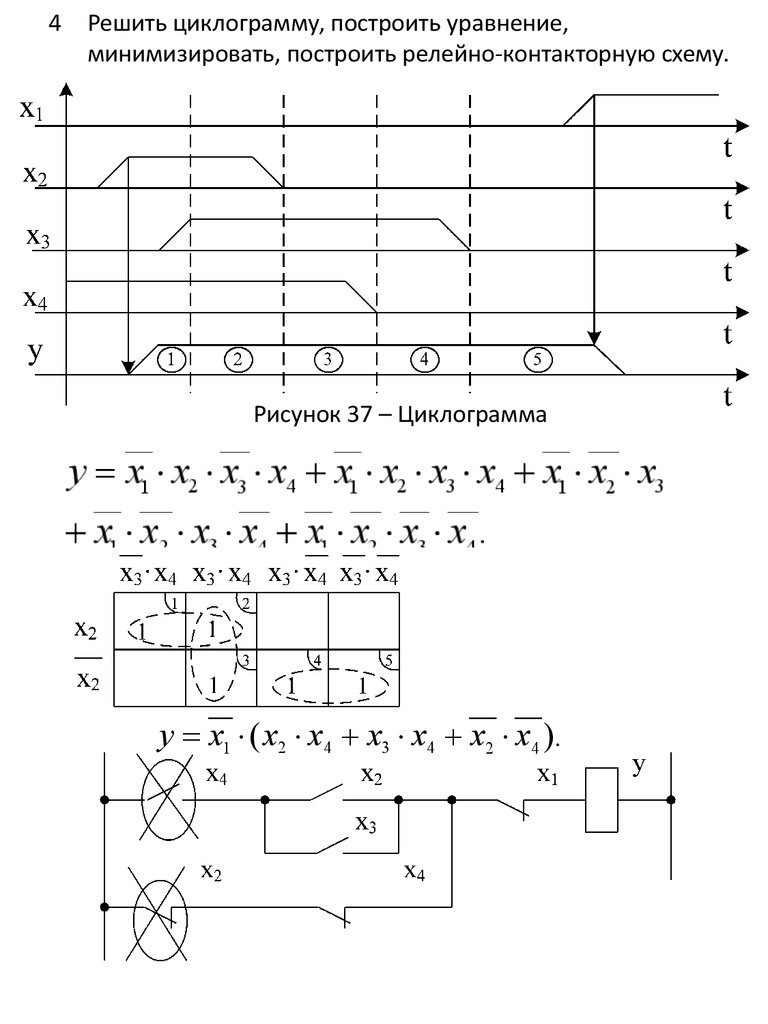
4 Решить циклограмму, построить уравнение,
минимизировать, построить релейно-контакторную схему.
Рисунок 37 – Циклограмма
у х1 ( х2 х4 х3 х4 х2 х4 ).

24.

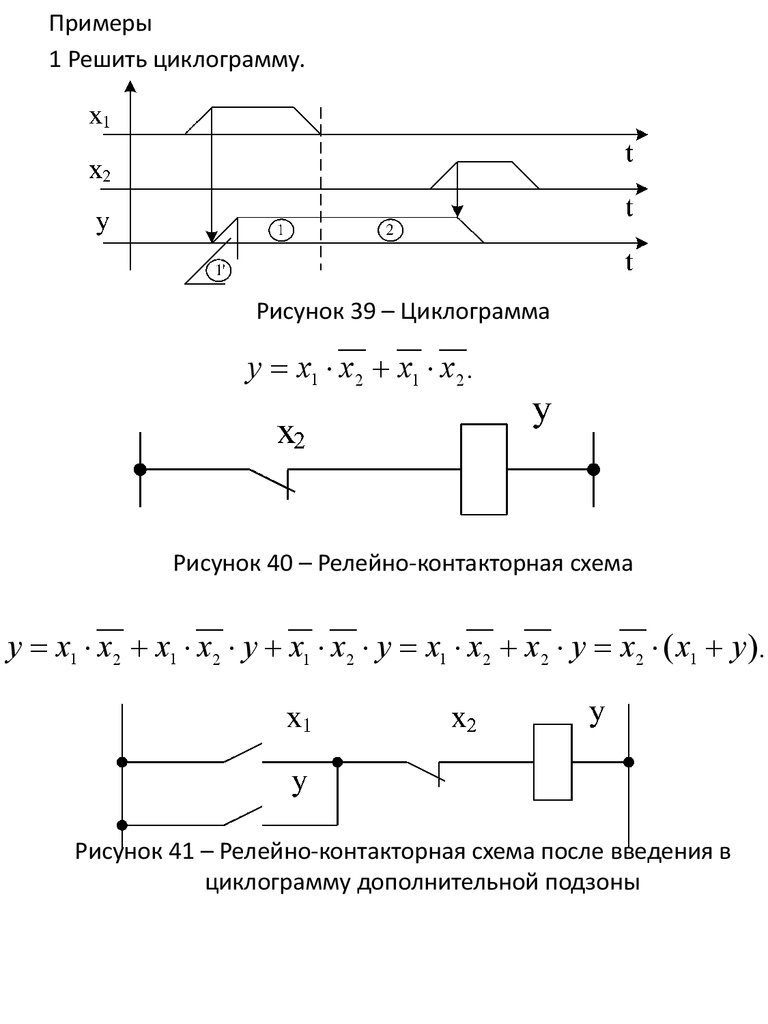
Примеры
1 Решить циклограмму.
Рисунок 39 – Циклограмма
у х1 х2 х1 х2 .
Рисунок 40 – Релейно-контакторная схема
у х1 х2 х1 х2 у х1 х2 у х1 х2 х2 у х2 ( х1 у).
Рисунок 41 – Релейно-контакторная схема после введения в
циклограмму дополнительной подзоны

25.

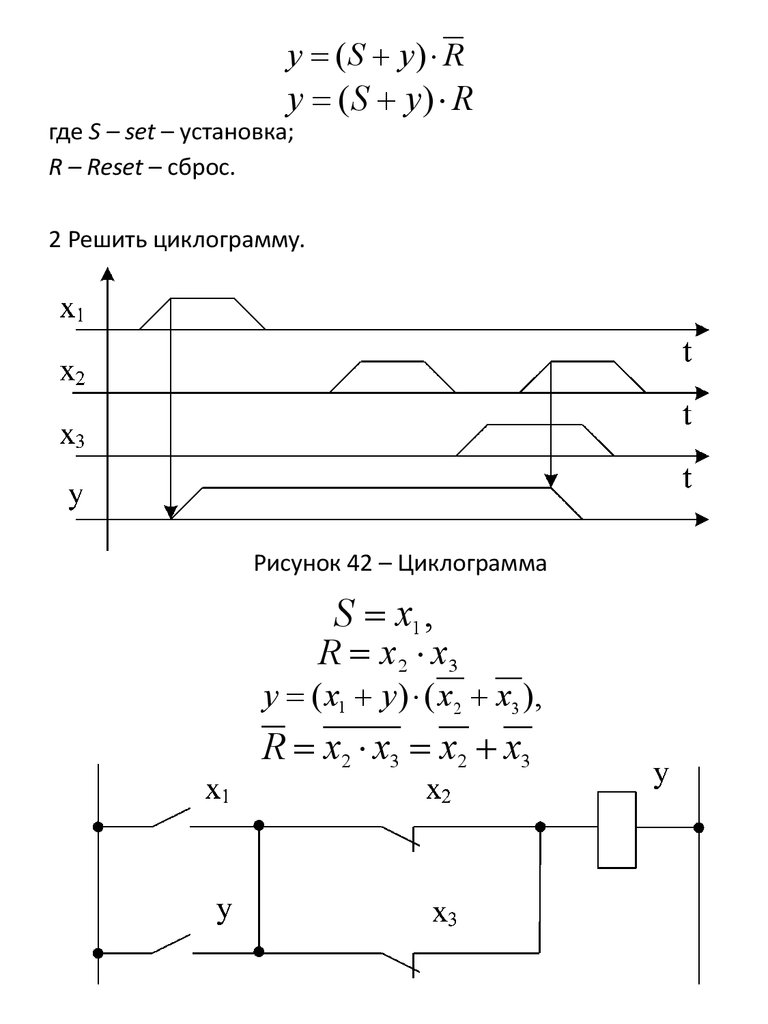
у (S y) R
у (S y) R
где S – set – установка;
R – Reset – сброс.
2 Решить циклограмму.
Рисунок 42 – Циклограмма
S x1 ,
R x 2 x3
у ( х1 у ) ( х2 х3 ),
R х2 х3 х2 х3

26.

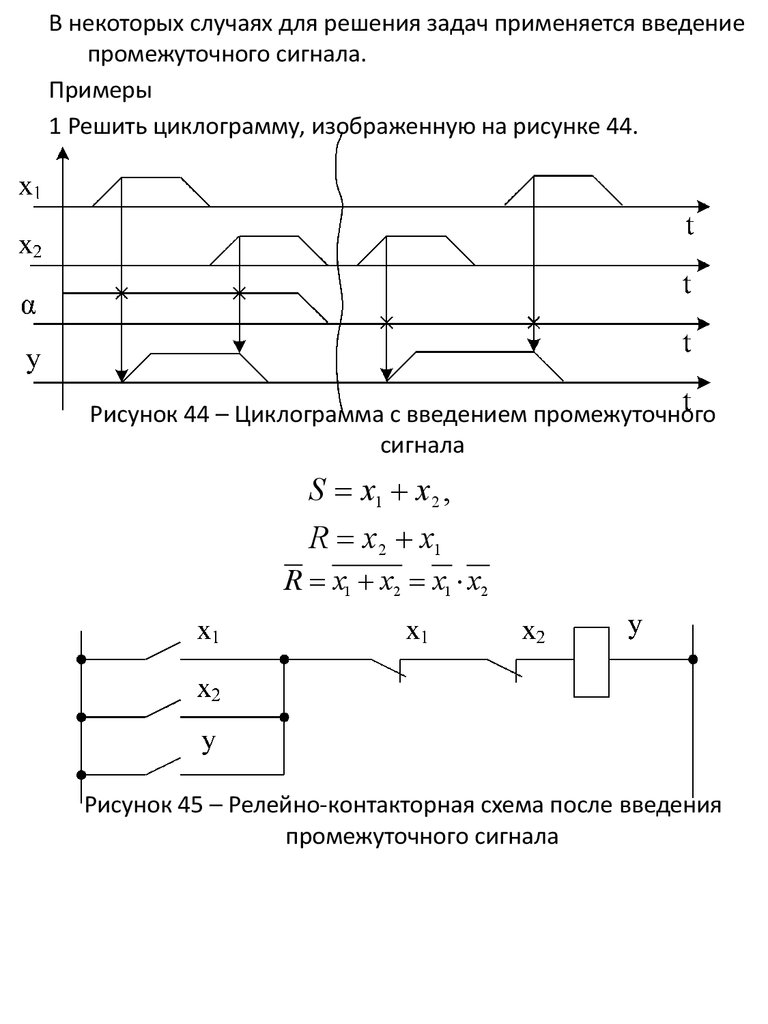
В некоторых случаях для решения задач применяется введение
промежуточного сигнала.
Примеры
1 Решить циклограмму, изображенную на рисунке 44.
Рисунок 44 – Циклограмма с введением промежуточного
сигнала
S x1 х2 ,
R x2 x1
R х1 х2 х1 х2
Рисунок 45 – Релейно-контакторная схема после введения
промежуточного сигнала

27.

S x1 x2 ,
R x1 х2 ,
R х1 х2 х1 х2 ( х1 ) ( х2 ),
у ( х1 х2 у) ( х1 ) ( х2 ),
где α – промежуточный сигнал.
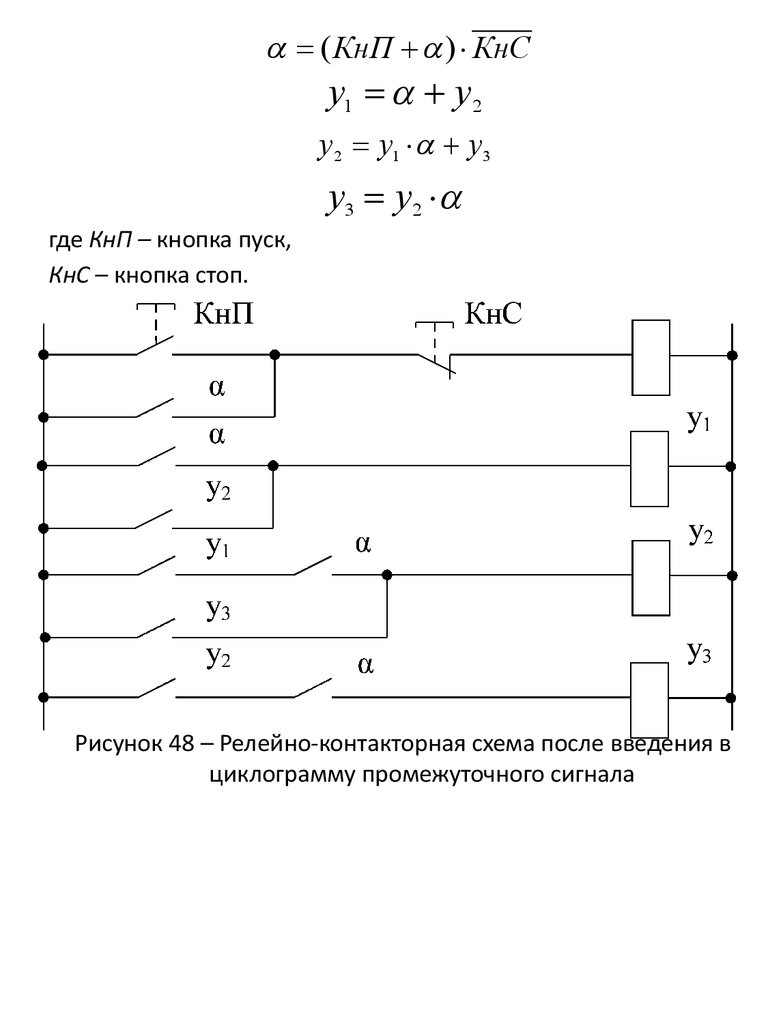
2 Создать схему, обеспечивающую прямую последовательность
включения сигналов в начале цикла и обратную при его
окончании.
Рисунок 46 – Циклограмма
Рисунок 47 – Циклограмма с использованием промежуточного
сигнала

28.

( КнП ) КнС
у1 у 2
у 2 у1 у3
у3 у2
где КнП – кнопка пуск,
КнС – кнопка стоп.
Рисунок 48 – Релейно-контакторная схема после введения в
циклограмму промежуточного сигнала

29.

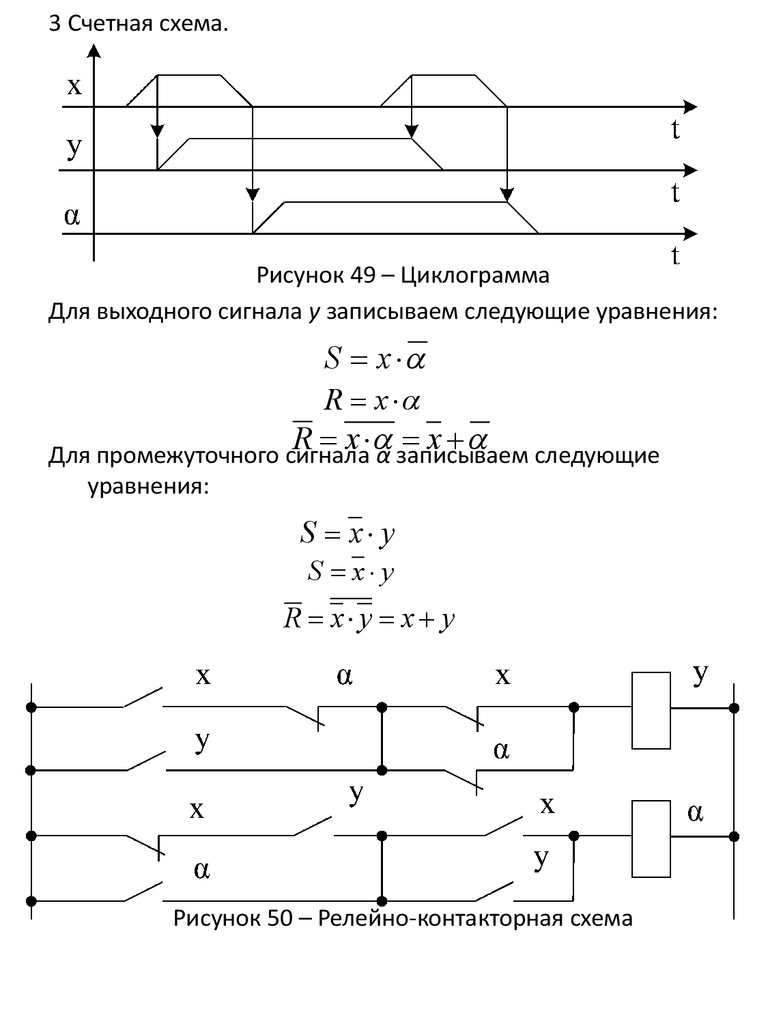
3 Счетная схема.
Рисунок 49 – Циклограмма
Для выходного сигнала у записываем следующие уравнения:
S x
R x
R х х
Для промежуточного сигнала α записываем следующие
уравнения:
S х у
S х у
R х у х у
Рисунок 50 – Релейно-контакторная схема

30.

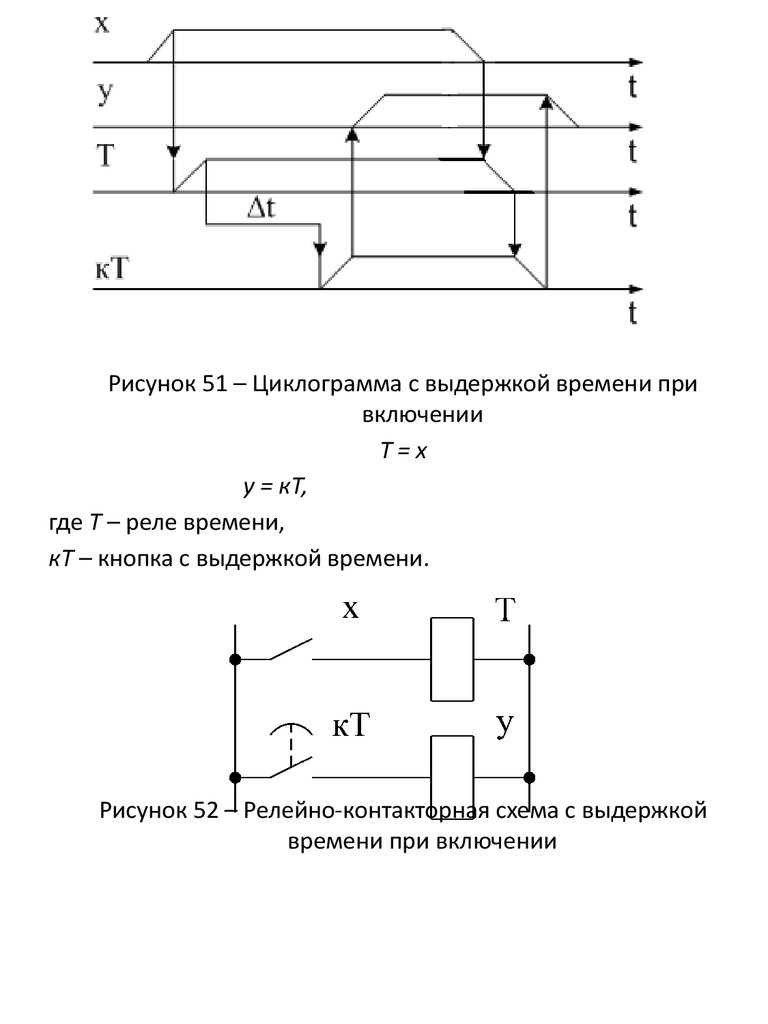
Рисунок 51 – Циклограмма с выдержкой времени при
включении
Т=х
у = кТ,
где Т – реле времени,
кТ – кнопка с выдержкой времени.
Рисунок 52 – Релейно-контакторная схема с выдержкой
времени при включении

31.

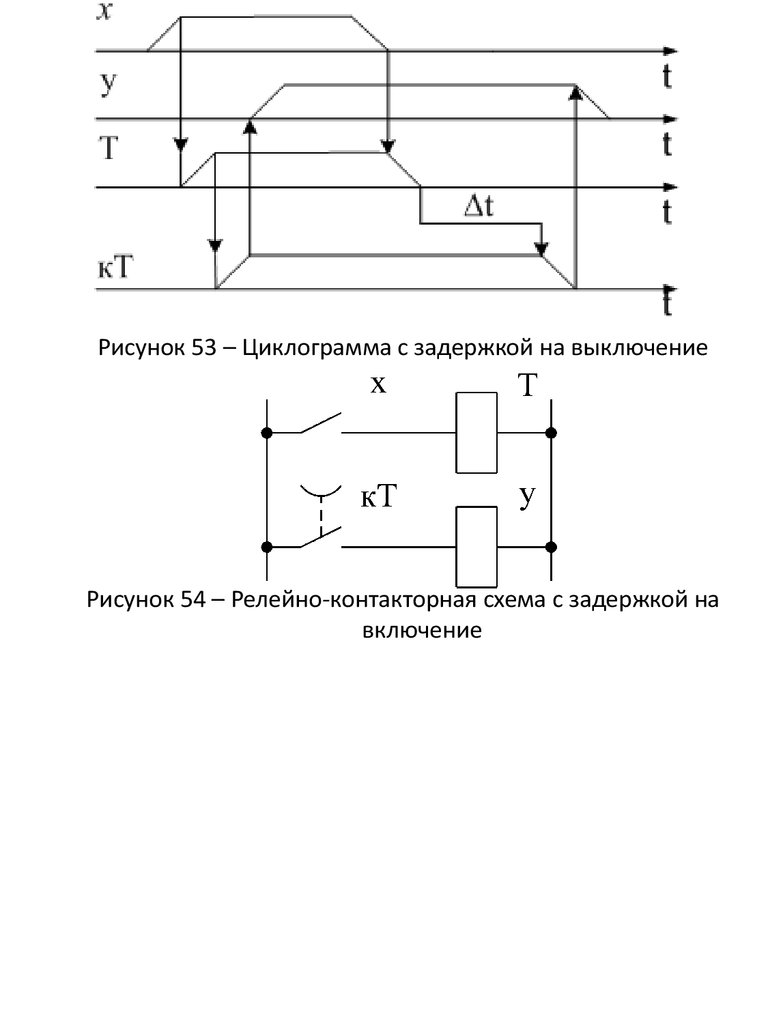
Рисунок 53 – Циклограмма с задержкой на выключение
Рисунок 54 – Релейно-контакторная схема с задержкой на
включение

32.

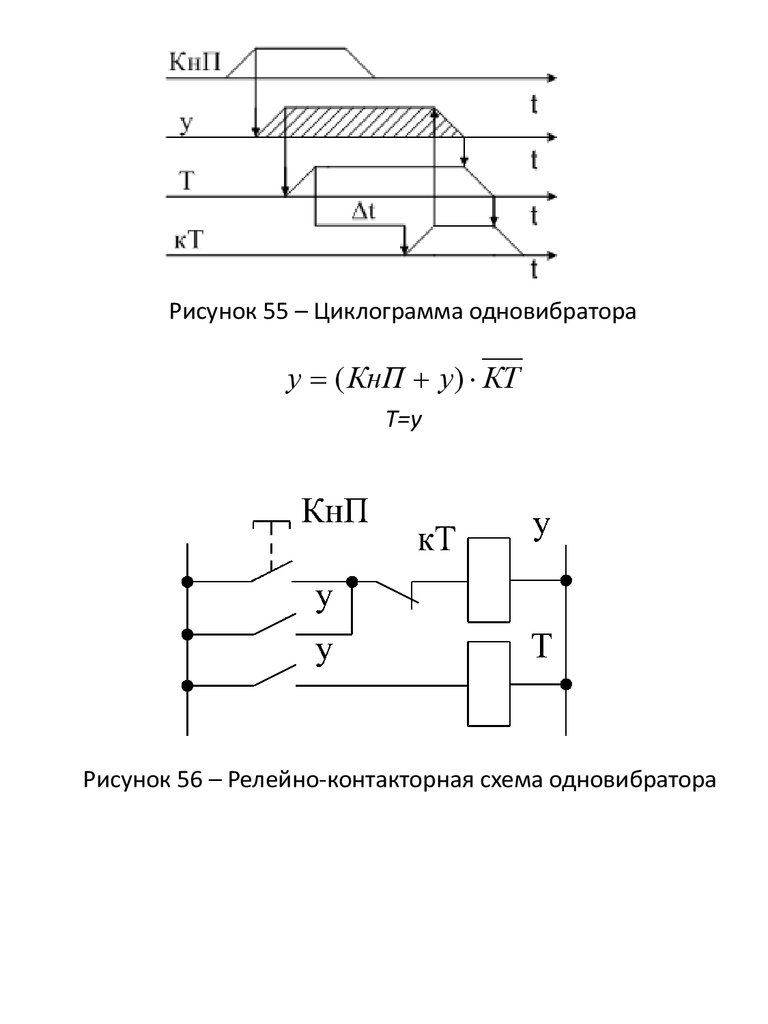
Рисунок 55 – Циклограмма одновибратора
y ( КнП у ) КТ
Т=у
Рисунок 56 – Релейно-контакторная схема одновибратора

33.

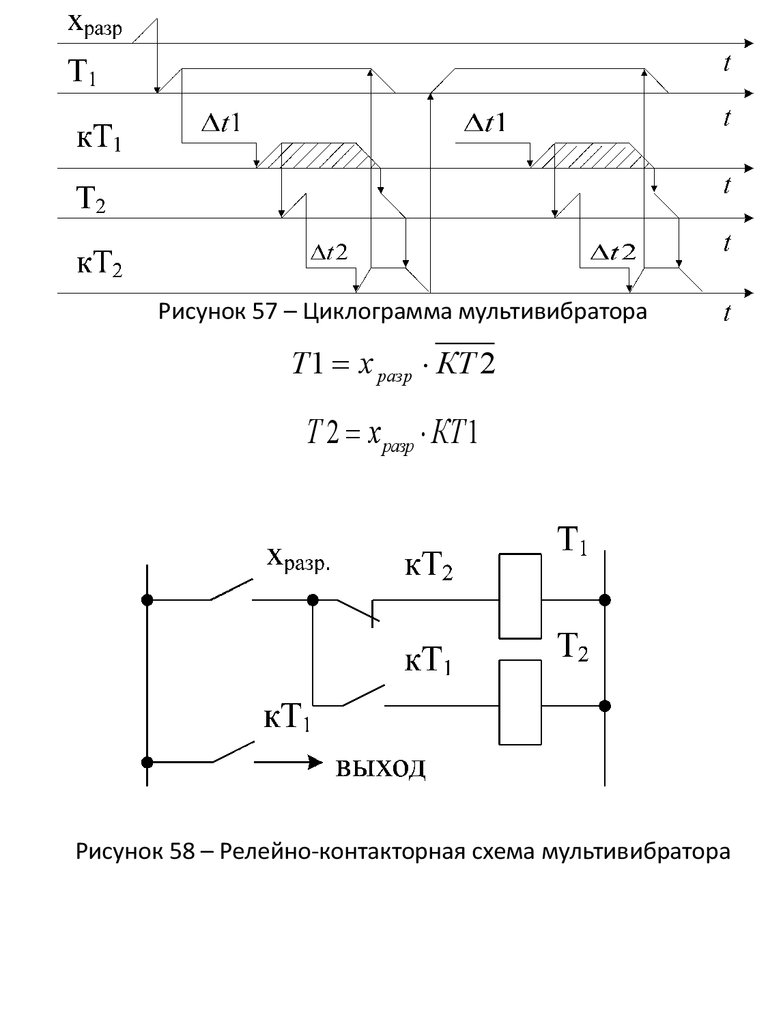
Рисунок 57 – Циклограмма мультивибратора
Т 1 х разр КТ 2
Т 2 х разр КТ 1
Рисунок 58 – Релейно-контакторная схема мультивибратора

34.

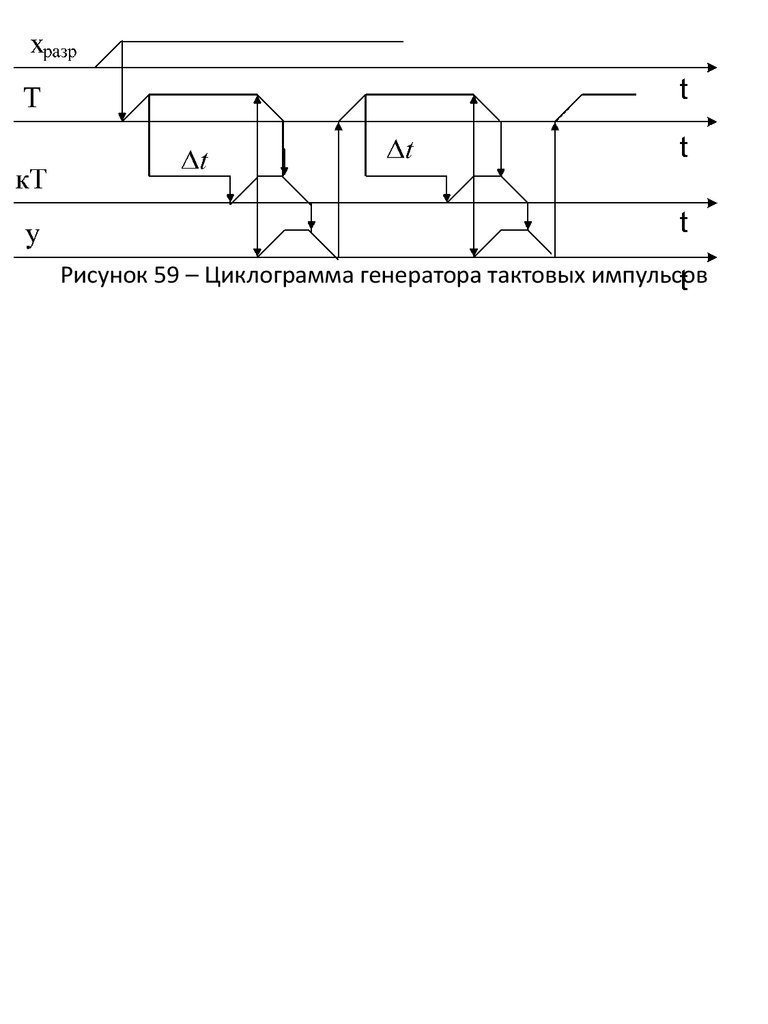
Рисунок 59 – Циклограмма генератора тактовых импульсов

35.

2.7 Примеры проектирования дискретных устройств
электроавтоматики
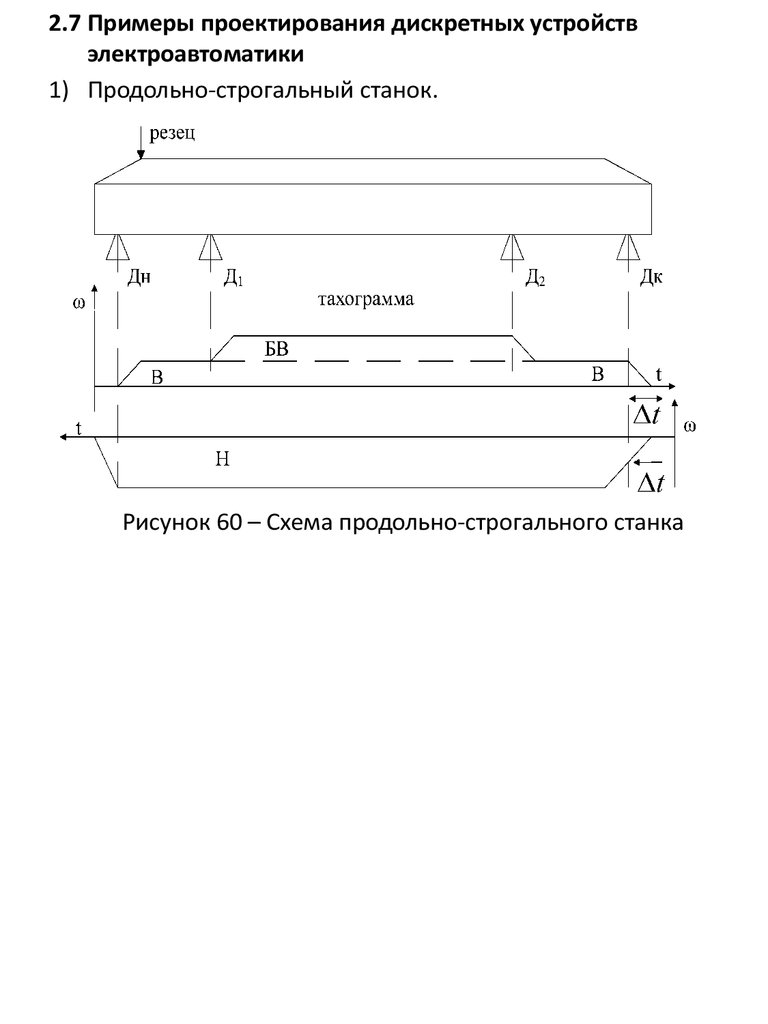
1) Продольно-строгальный станок.
Рисунок 60 – Схема продольно-строгального станка

36.

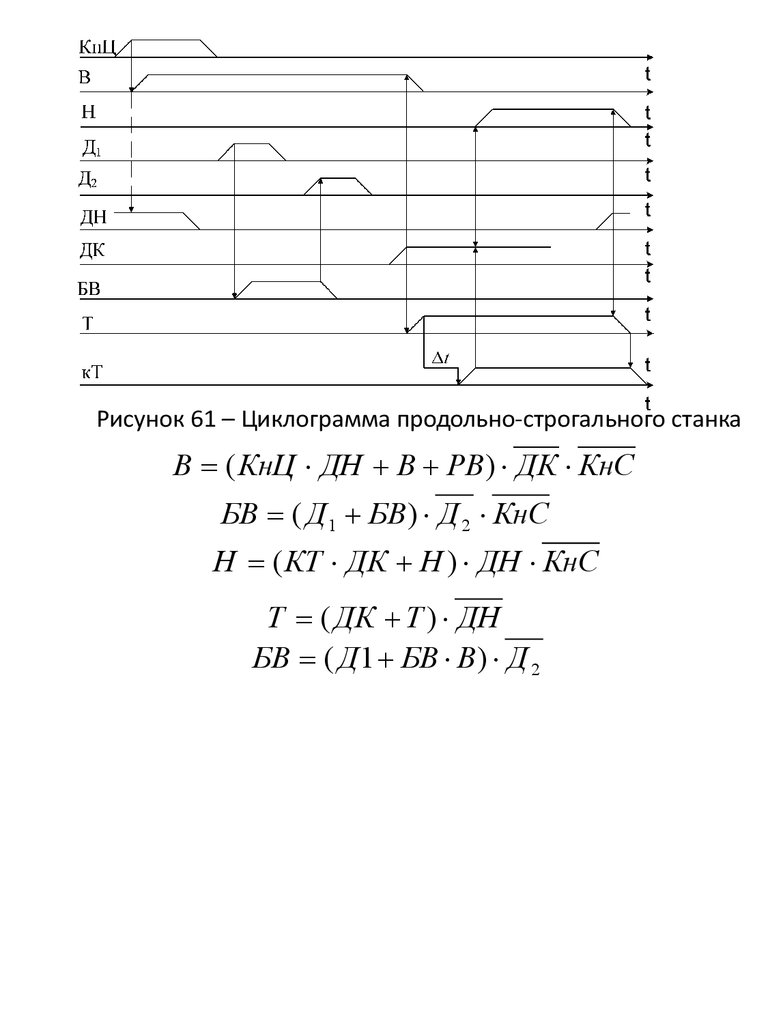
Рисунок 61 – Циклограмма продольно-строгального станка
В ( КнЦ ДН В РВ) ДК КнС
БВ ( Д 1 БВ ) Д 2 КнС
Н ( КТ ДК Н ) ДН КнС
Т ( ДК Т ) ДН
БВ ( Д 1 БВ В ) Д 2

37.

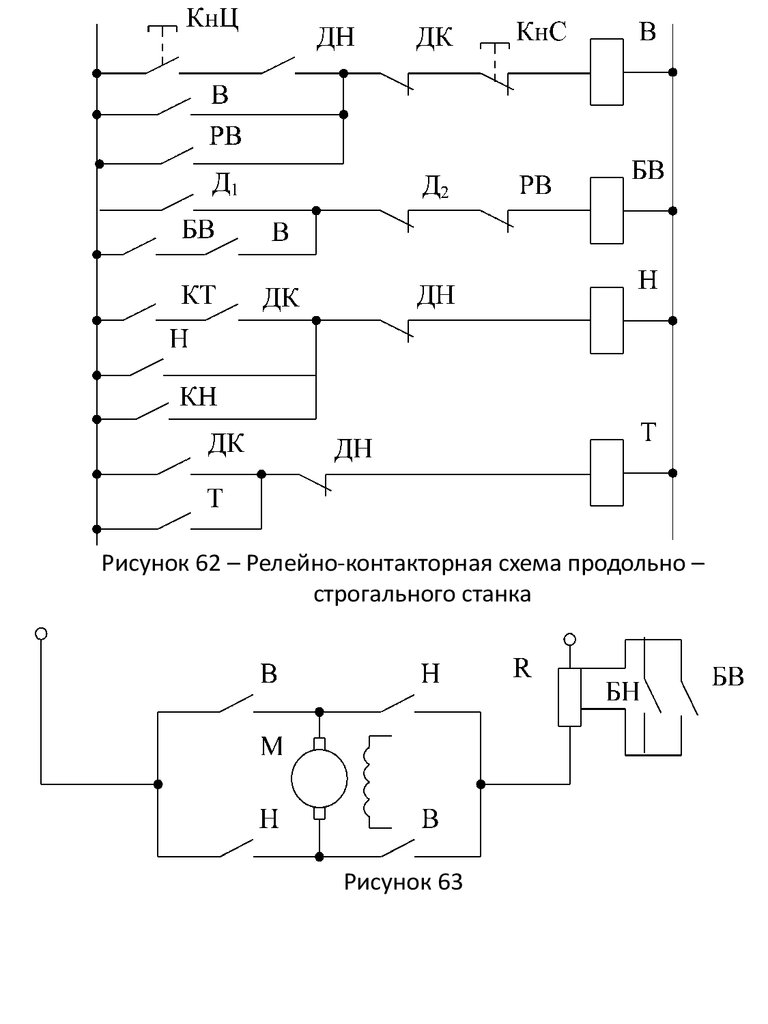
Рисунок 62 – Релейно-контакторная схема продольно –
строгального станка
Рисунок 63

38.

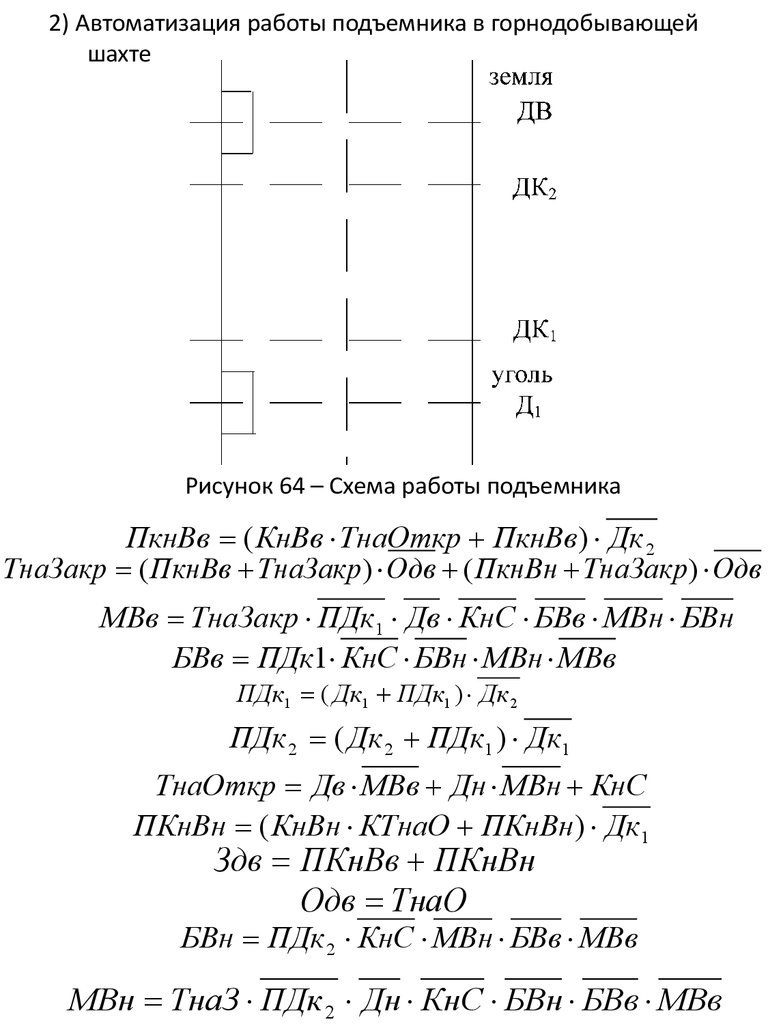
2) Автоматизация работы подъемника в горнодобывающей
шахте
Рисунок 64 – Схема работы подъемника
ПкнВв ( КнВв ТнаОткр ПкнВв) Дк 2
ТнаЗакр ( ПкнВв ТнаЗакр ) Одв ( ПкнВн ТнаЗакр ) Одв
МВв ТнаЗакр ПДк1 Дв КнС БВв МВн БВн
БВв ПДк1 КнС БВн МВн МВв
ПДк1 ( Дк1 ПДк1 ) Дк 2
ПДк 2 ( Дк 2 ПДк1 ) Дк1
ТнаОткр Дв МВв Дн МВн КнС
ПКнВн ( КнВн КТнаО ПКнВн) Дк1
Здв ПКнВв ПКнВн
Одв ТнаО
БВн ПДк 2 КнС МВн БВв МВв
МВн ТнаЗ ПДк 2 Дн КнС БВн БВв МВв