Похожие презентации:
Квадратичная функция. 8 класс
1.
«Функции у=ах2 +bx+c»8 класс
2. Девиз урока:
«Дорогу осилитидущий, а математикумыслящий»
3. Цели урока:
1. Закрепить свойства функцииу=ах2 и построение ее графика.
2. Научиться строить графики
функций у = а х2 + с
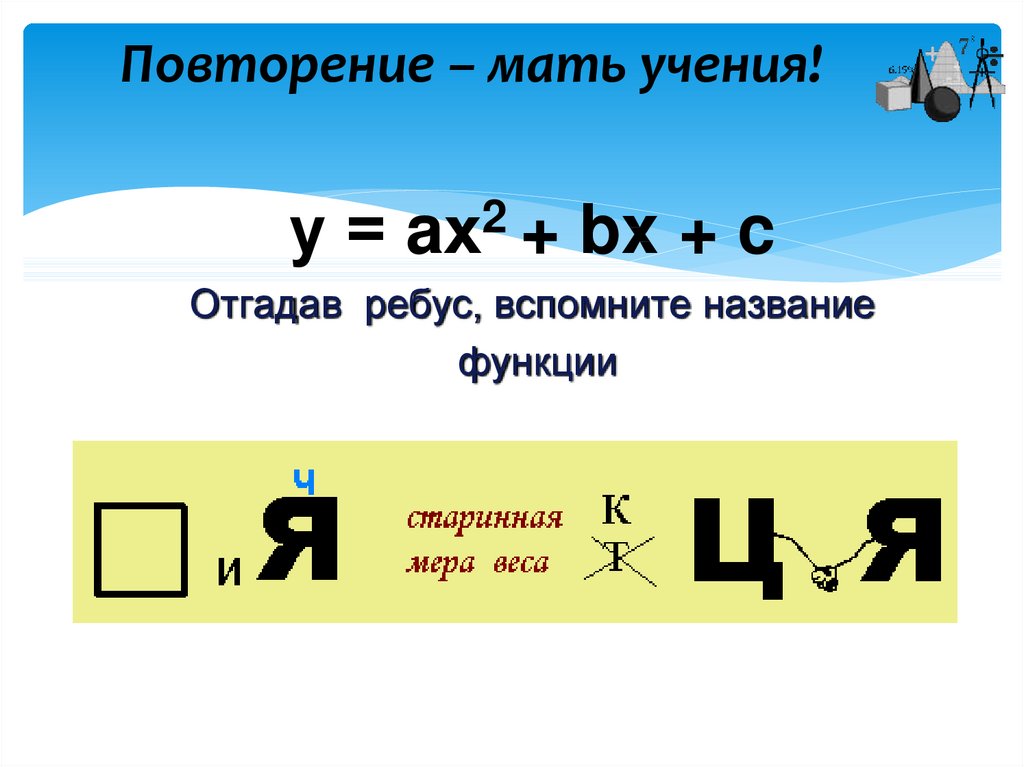
4. Повторение – мать учения!
у = aх2 + bx + cОтгадав ребус, вспомните название
функции
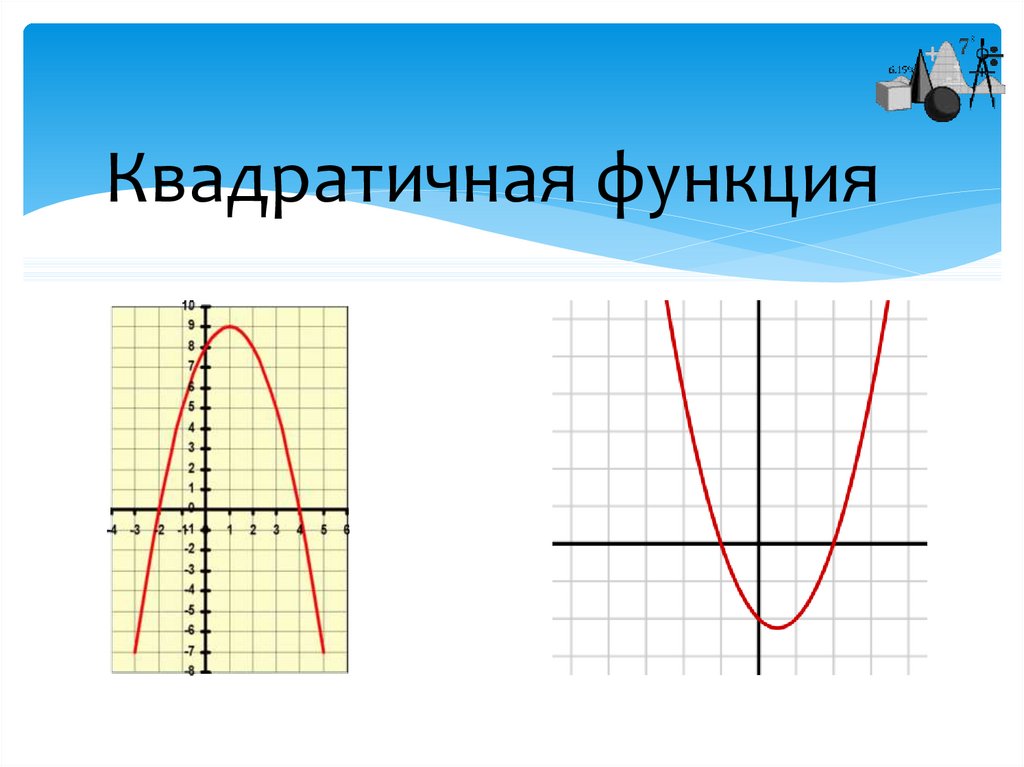
5. Квадратичная функция
6. МОЗГОВОЙ ШТУРМ
ПОВТОРЕНИЕ ПО ТЕМЕ«КВАДРАТИЧНАЯ ФУНКЦИЯ»
7. Подумай…
Из приведенных примеров выберите те функции,которые являются квадратичными. Для
квадратичных функций назовите коэффициенты.
2
y
1
x
y 2x x
2
y 4x
2
y x 7 x 1
3
8. Ответить на вопросы
Сформулировать определениеквадратичной функции;
Что является графиком квадратичной
функции?
Сформулировать свойства квадратичной
функции у=ах2 при а>0, a<0.
9.
Выберите правильный ответ:Какая функция называется квадратичной?
1.
y x
n
где x - независимая переменная,
n-натуральное число.
y ax bx c
2
2.
где х - независимая
переменная,c – некоторые
числа, причем а ≠0.
y kx b
3.
где х – независимая
переменная, k, и – числа.
ПРОВЕРЯЕМ
10.
Выберите правильный ответ:Графиком квадратичной функции является:
1. ГИПЕРБОЛА
2. ПРЯМАЯ
3. ПАРАБОЛА
ПРОВЕРЯЕМ
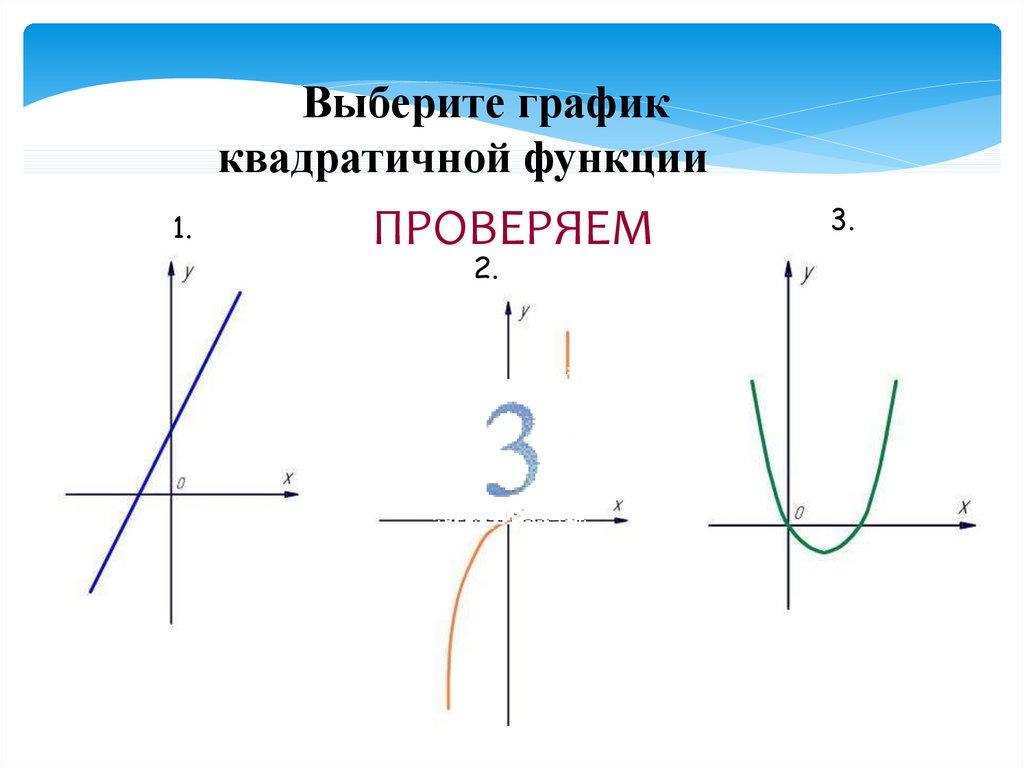
11.
Выберите графикквадратичной функции
1.
ПРОВЕРЯЕМ
2.
3.
12.
Выберите свойства для функции2
y ax , при a 0
1. Если х=0, то у=0. График проходит
ПРОВЕРЯЕМ
через начало координат.
2. Функция убывает в промежутке [0;+∞)
и возрастает в промежутке (-∞;0].
3. Если y>0, то график функции
расположен в верхней полуплоскости.
13. Заполни пропуски …
1. Функция вида…..
называется
где а, b, c – заданные …….
квадратичной ,
, а … 0.
у = aх2 + bx + c, действительныу числа, а 0
2. Графиком квадратичной функции при любом а … 0 называют
…..
а 0, параболой
3. Точку пересечения графика квадратичной функции с осью
симметрии Oy называют …
вершиной параболы
4. При а >0 ветви ……….. у = ах2 направлены … .
параболы,
вверх
5. Если а < о и х 0, то функция у = ах2 принимает …
(положительные или отрицательные) значения.
отрицательные
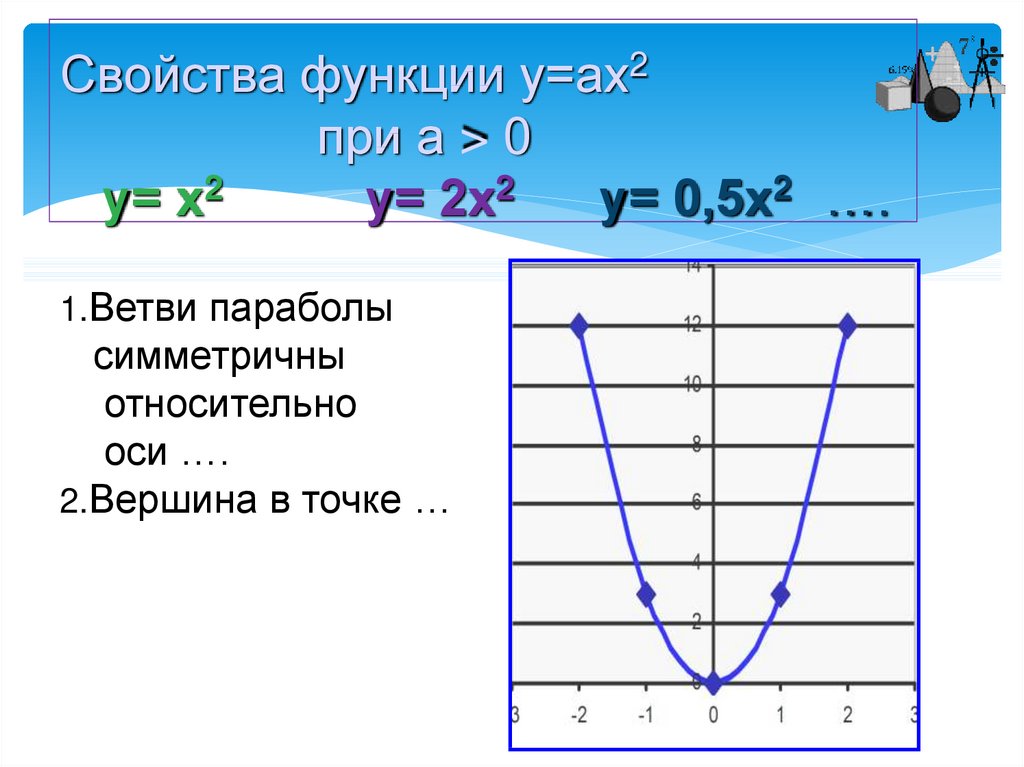
14. Свойства функции у=ах2 при а > 0 у= х2 у= 2х2 у= 0,5х2 …. 1.Ветви параболы симметричны относительно оси …. 2.Вершина в точке …
Свойства функции у=ах2при а > 0
у= х2
у= 2х2
у= 0,5х2 ….
1.Ветви параболы
симметричны
относительно
оси ….
2.Вершина в точке …
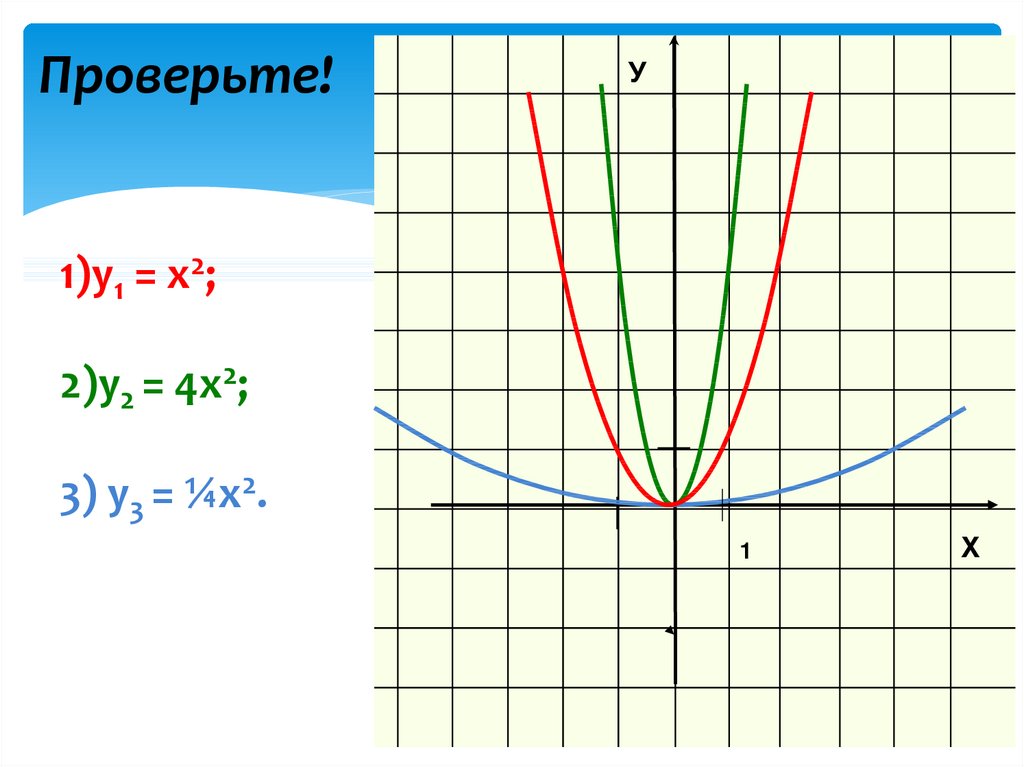
15. Определите по коэффициенту «сжатие или растяжение»?
Какой получится графикзаданных функций относительно
графика у = х2 :
1) у = 4х2;
2) у = ¼х2 ?
16. Проверьте! 1)y1 = х2; 2)у2 = 4х2; 3) у3 = ¼х2.
Проверьте!У
1)y1 = х2;
2)у2 = 4х2;
3) у3 = ¼х2.
1
Х
17. Функция у= ах2 и её свойства. у =х2
18. Квадратичная функция!
Общий виду = aх2 + bx + c
Если b=0, то функция примет вид
у = aх2 + с
Рассмотрим
построение
графика
этой
функции в зависимости от знака с!
19.
yy = x2
4
x
0
1
2
y
0
1
4
3
2
y = x2 - 2
1
x
-1
1
2
3
x
0
1
2
y
-2
-1
2
-2
y = x2 + 4
В.П. (0;0)
В.П. (0;-2)
В.П. (0;4)
x
0
1
2
y
4
5
9
20.
22- 2
y
=
x
y
=
x
Сравним расположение графиков функций
и
График второй функции получен сдвигом графика первой функции вдоль
оси Оу на 2 единицы вниз.
2+ 4
y
=
x
Аналогично, график функции
получен сдвигом графика
функции
y=
x2
вдоль оси Оу на 4 единицы вверх.
21. Построение графиков квадратичных функций с помощью движения вдоль оси Оу
вд
о
л
ь
о
с
и
у
у=х2+с
↑на с
у=х2
↓на с
у=х2-с
22. Задание 1. Укажите координаты вершины параболы, которая получена сдвигом вдоль оси у:
параболы y = 3x2 на 2 ед. внизпараболы y = -4x2 на 1 ед. вверх
параболы y = 0,5x2 на 4 ед. вверх
параболы y = -0,1x2 на 3 ед. вниз
23. Задание 2. Постройте в одной координатной плоскости графики следующих функций и определите координату вершины параболы:
1) y =2
x -
3) y =
2
x +
3
1
2) y = -
2
x -
4
4) y = - х2 + 5
24.
Алгебра щедра. Зачастую она даетбольше, чем у нее спрашивают.”
Ж.Даламбер



















 Математика
Математика








