Похожие презентации:
Вписанные и описанные четырехугольники
1. Тема урока: Вписанные и описанные четырехугольники
2.
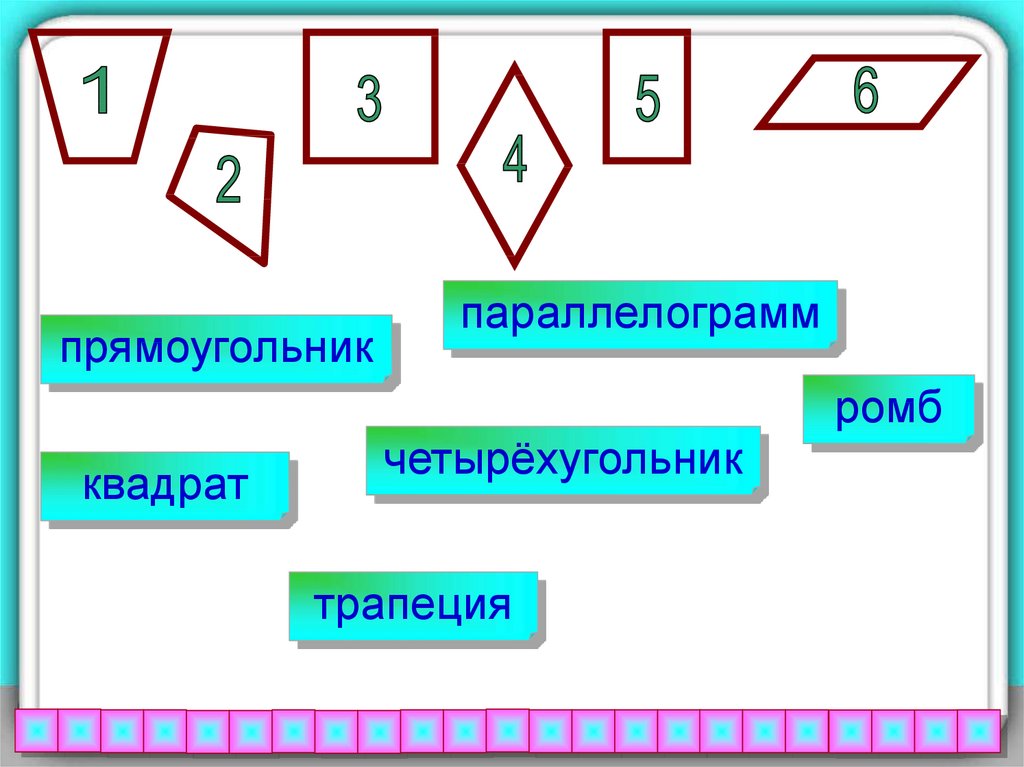
Задание: Вспомните определениявсех четырёхугольников и
распределите названия фигур по
местам
Помните: у одной фигуры может быть несколько
названий.
3.
прямоугольникпараллелограмм
ромб
квадрат
четырёхугольник
трапеция
4.
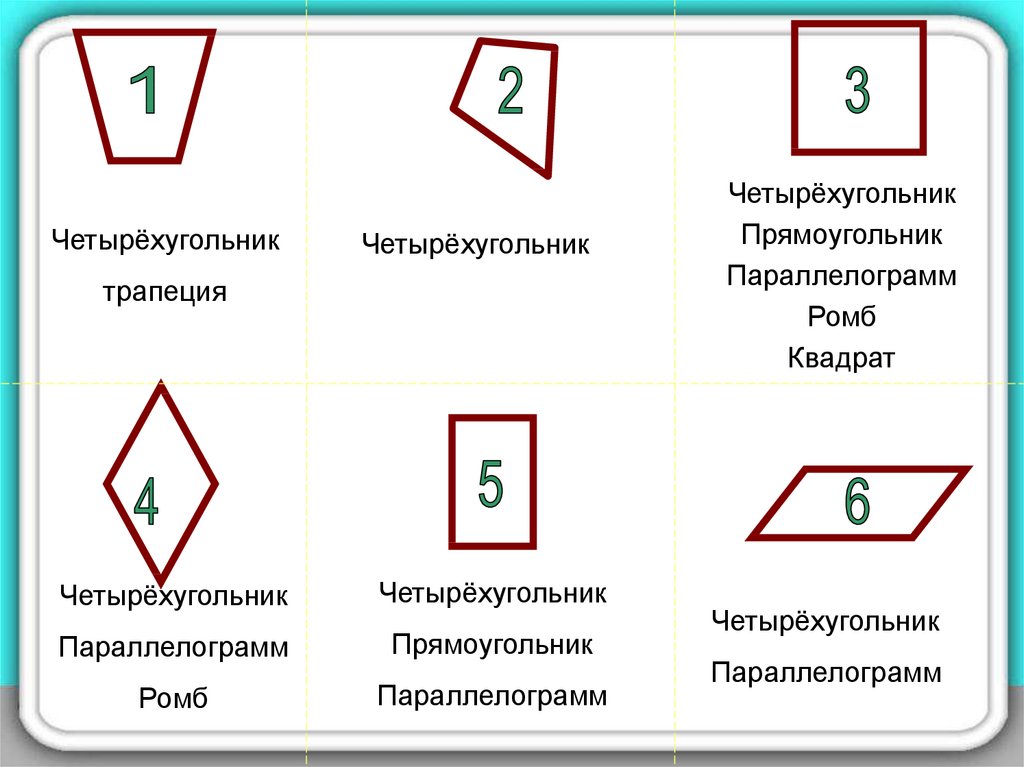
ЧетырёхугольникЧетырёхугольник
трапеция
Четырёхугольник
Четырёхугольник
Параллелограмм
Прямоугольник
Ромб
Параллелограмм
Четырёхугольник
Прямоугольник
Параллелограмм
Ромб
Квадрат
Четырёхугольник
Параллелограмм
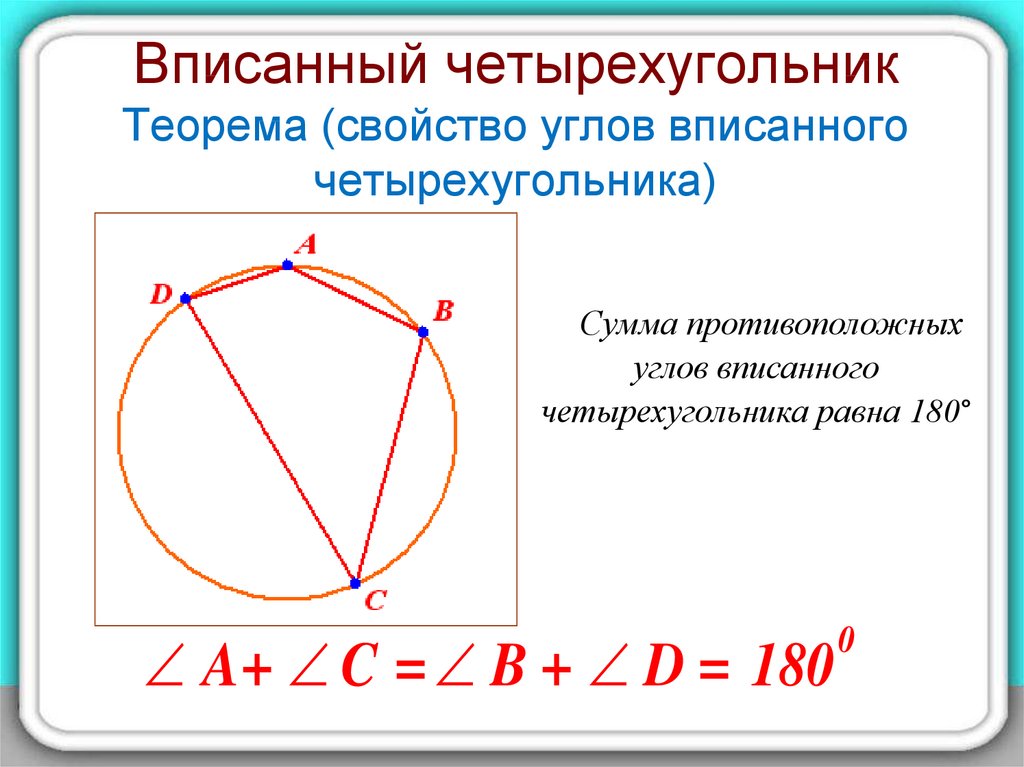
5. Вписанный четырехугольник Теорема (свойство углов вписанного четырехугольника)
Сумма противоположныхуглов вписанного
четырехугольника равна 180°
A+ C = B + D = 180
0
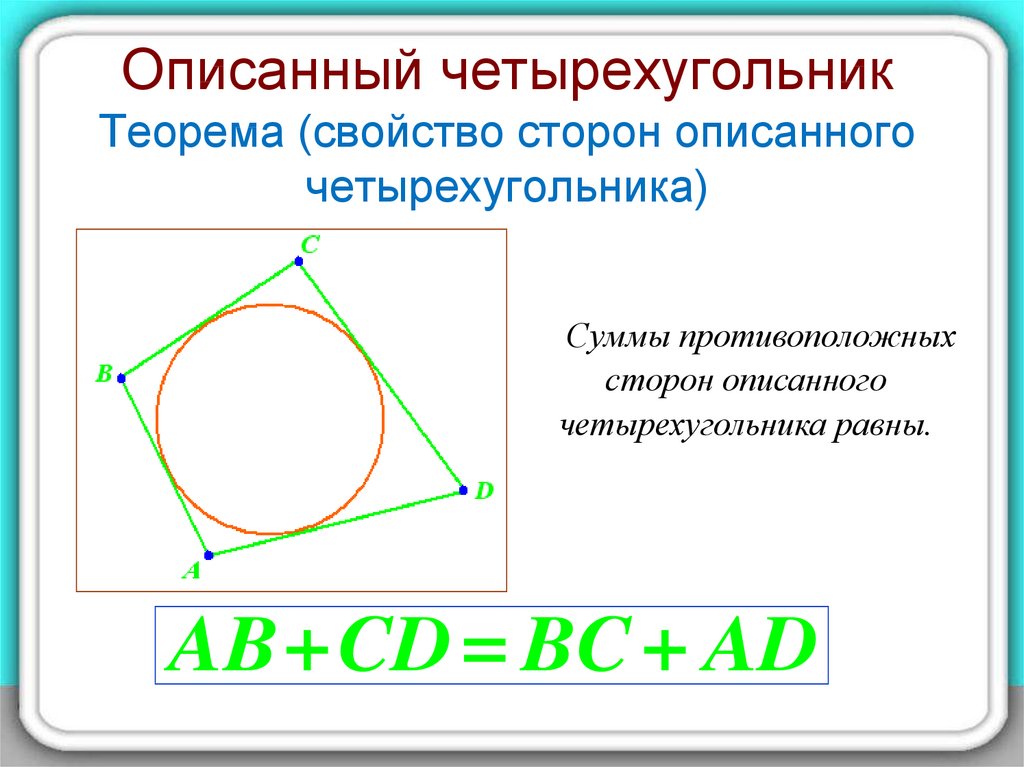
6. Описанный четырехугольник Теорема (свойство сторон описанного четырехугольника)
Суммы противоположныхсторон описанного
четырехугольника равны.
AB+CD = BC + AD
7. Примеры
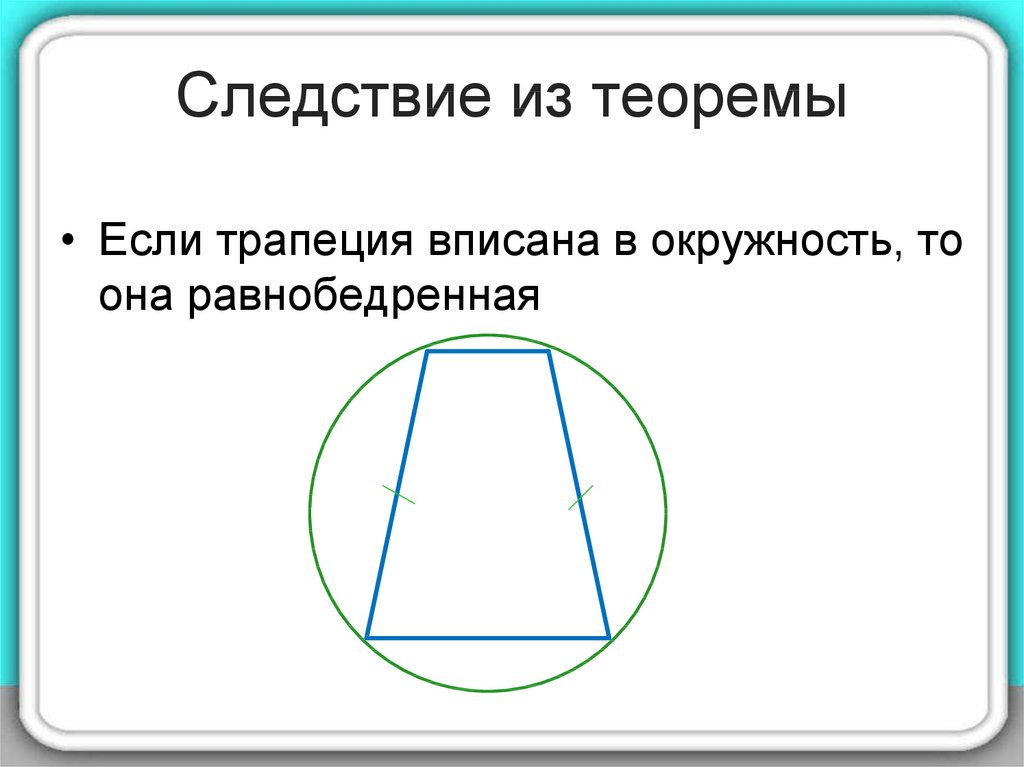
8. Следствие из теоремы
• Если трапеция вписана в окружность, тоона равнобедренная
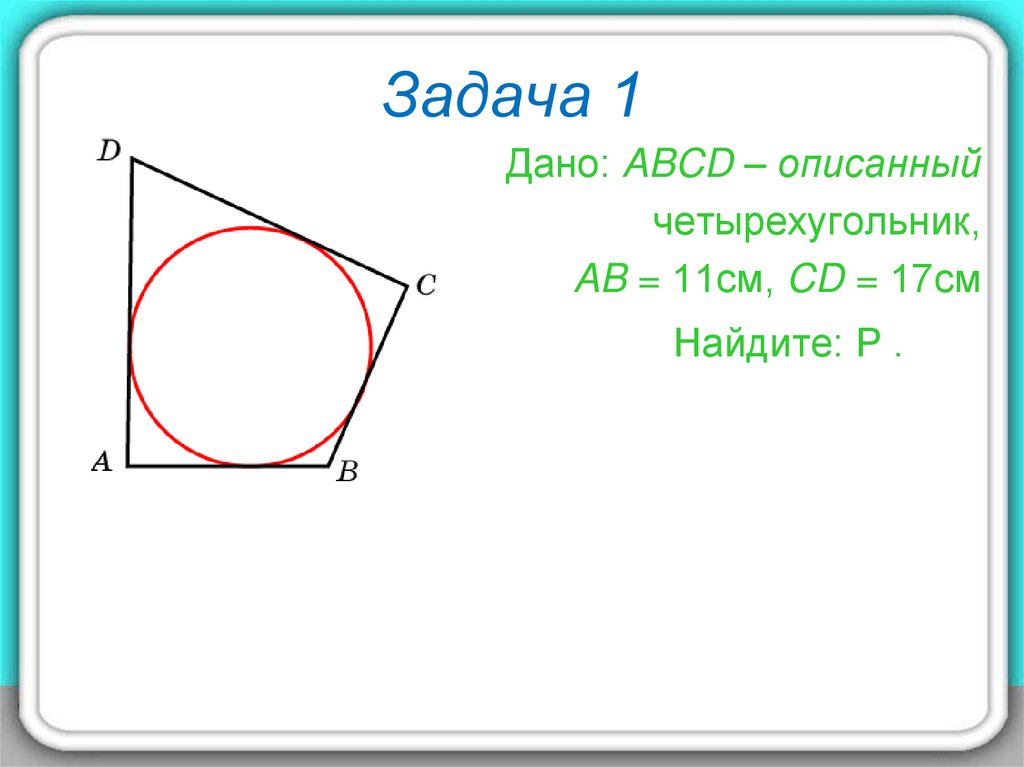
9. Задача 1
Дано: ABCD – описанныйчетырехугольник,
AB = 11см, CD = 17см
Найдите: Р .
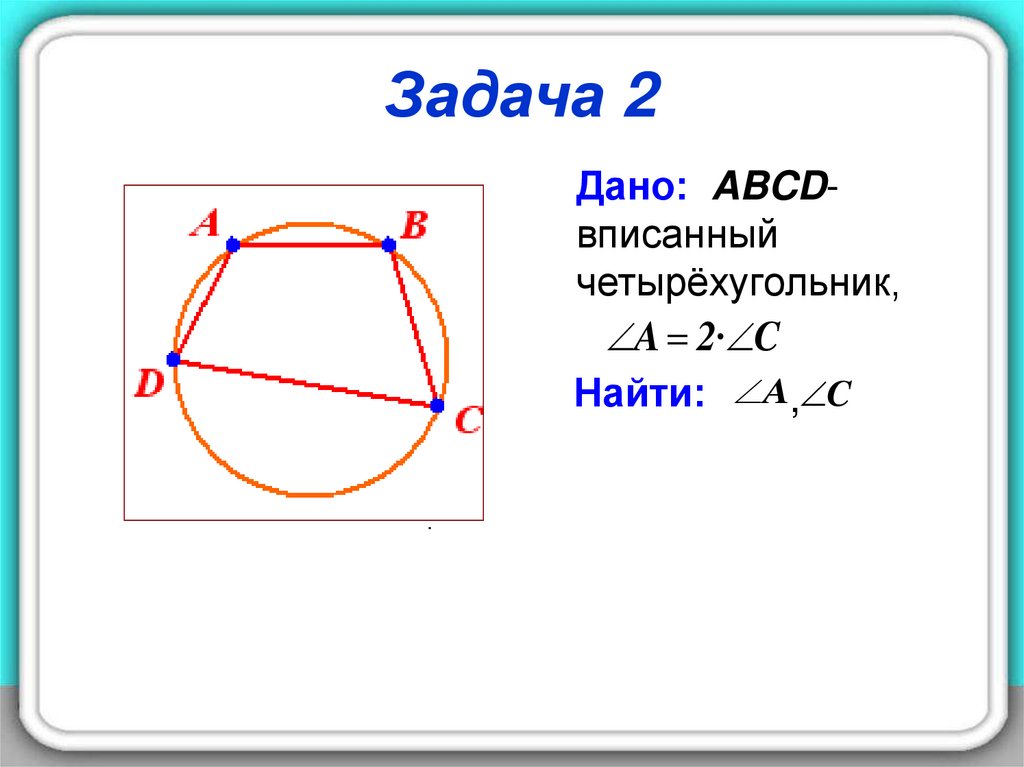
10. Задача 2
Дано: ABCDвписанныйчетырёхугольник,
A 2· C
Найти: A, C
.
11. Подведение итогов
1. Если суммы длин противоположных сторон выпуклогочетырехугольника равны, то в него можно вписать круг.
2. Если сумма смежных углов четырехугольника равна 180°,
то вокруг него можно описать окружность.
3. Четырехугольник вписан в окружность один из его углов
равен 65°, то противоположный угол равен 115°.
4. Если все стороны многоугольника касаются окружности, то
окружность называется описанная.
5. Если все стороны многоугольника касаются окружности,
то многоугольник называется описанным.
6. Если все вершины многоугольника лежат на окружности,
то окружность называется описанной.
7. Если все вершины многоугольника лежат на окружности,
то многоугольник называется вписанным.





 Математика
Математика








