Замечательные точки треугольника

1. Замечательные точки треугольника Урок 2. Теорема о серединном перпендикуляре.

2. Урок геометрии в 8 классе

Тема: Теорема о серединном перпендикуляре
Цели:
ввести понятие серединного перпендикуляра к
отрезку;
рассмотреть теорему о серединном
перпендикуляре и следствие из него;
Формировать умения применять известные знания
в незнакомой ситуации, сравнивать,
анализировать, обобщать.

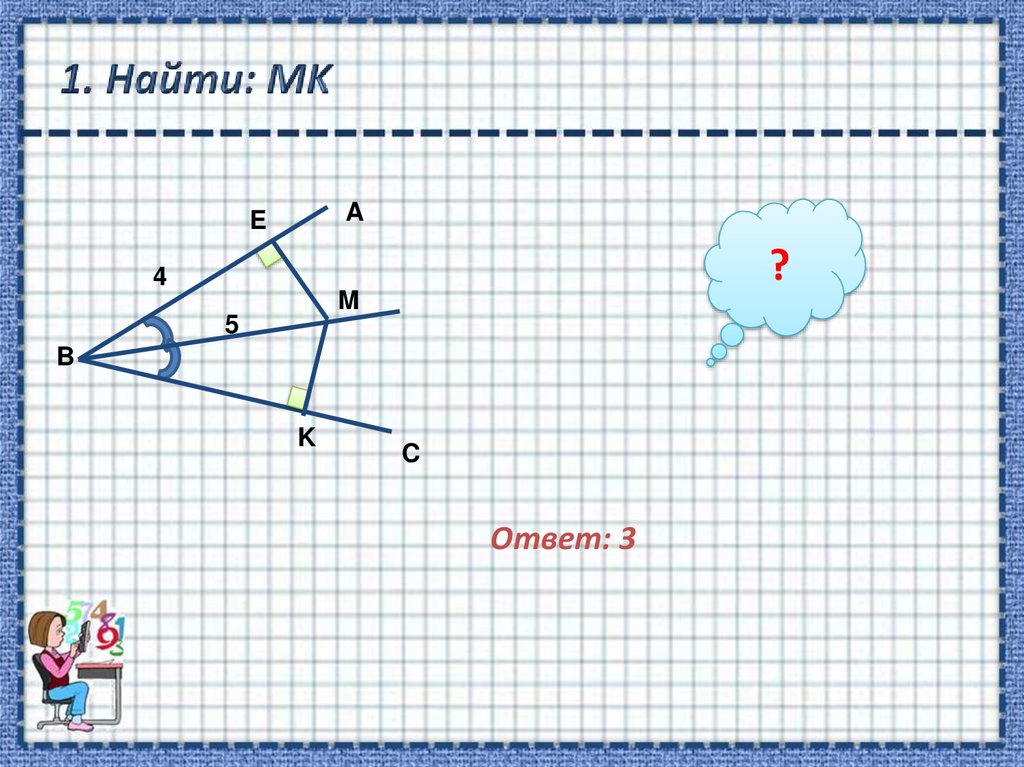
3. 1. Найти: MK

A
E
?
4
M
5
B
K
C
Ответ: 3

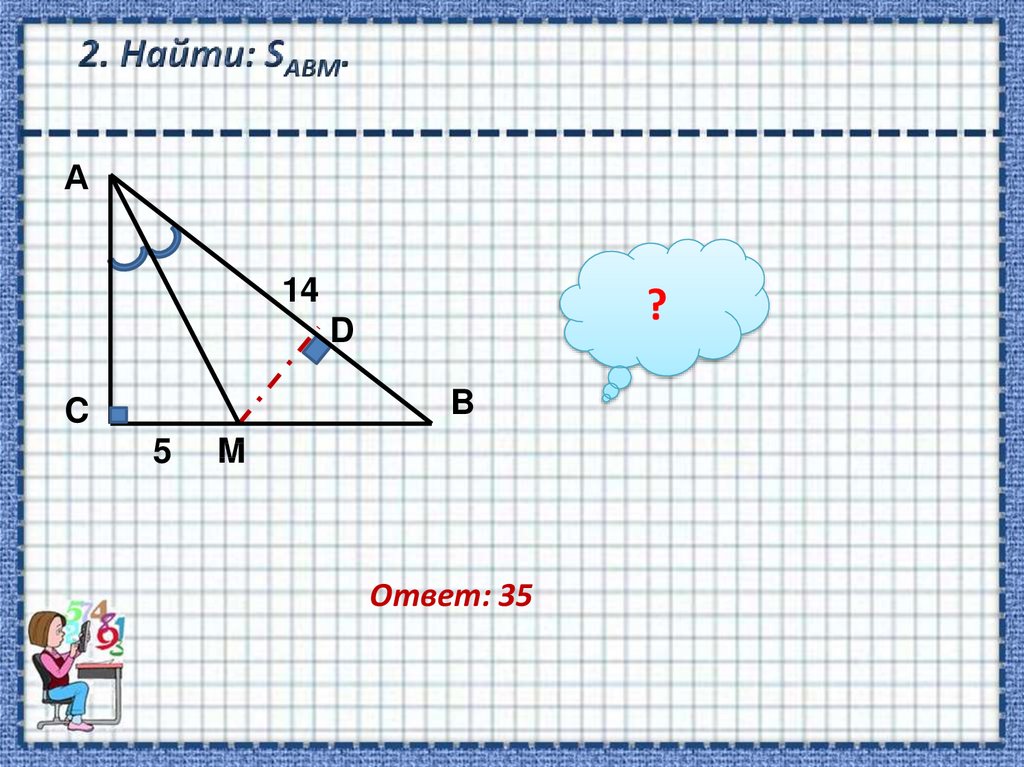
4. 2. Найти: SАВM.

А
14
?
D
B
C
5
M
Ответ: 35

5.

Геометрия - удивительная наука. Её история
насчитывает не одно тысячелетие, но каждая
встреча с ней способна одарить и обогатить
волнующей новизной маленького открытия,
изумляющей радостью творчества.
Действительно, любая задача элементарной
геометрии является, по существу, теоремой,
а ее решение – скромной (а иногда и огромной)
математической победой.

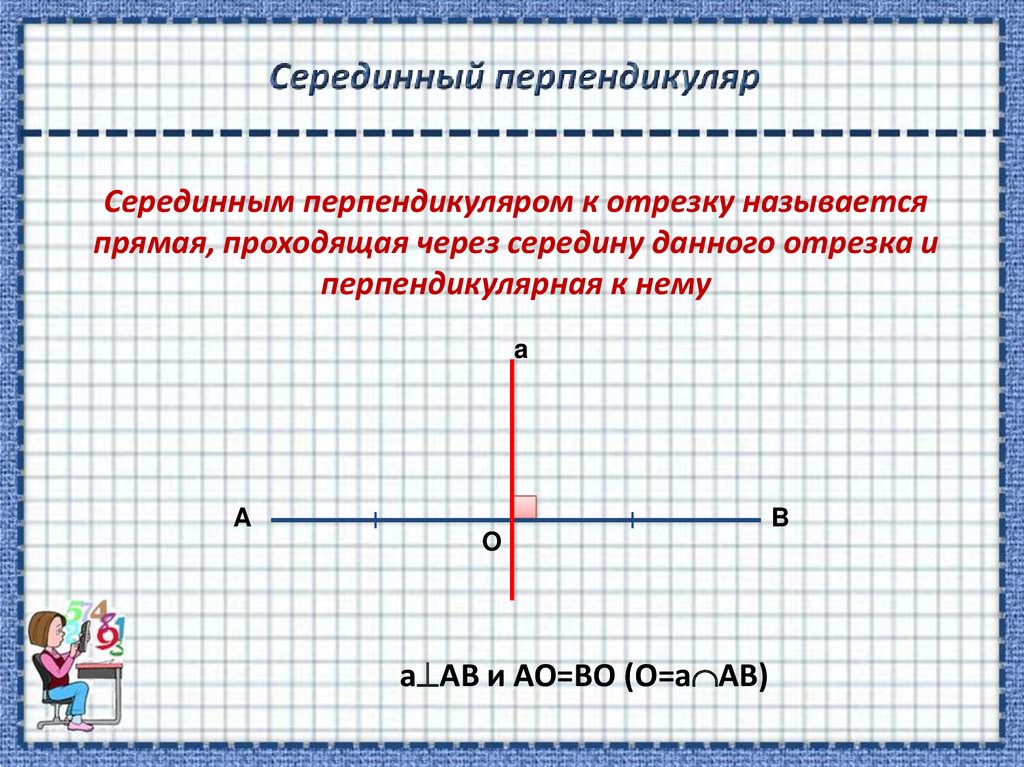
6. Серединный перпендикуляр

Серединным перпендикуляром к отрезку называется
прямая, проходящая через середину данного отрезка и
перпендикулярная к нему
a
A
B
O
а АВ и АО=ВО (О=а АВ)

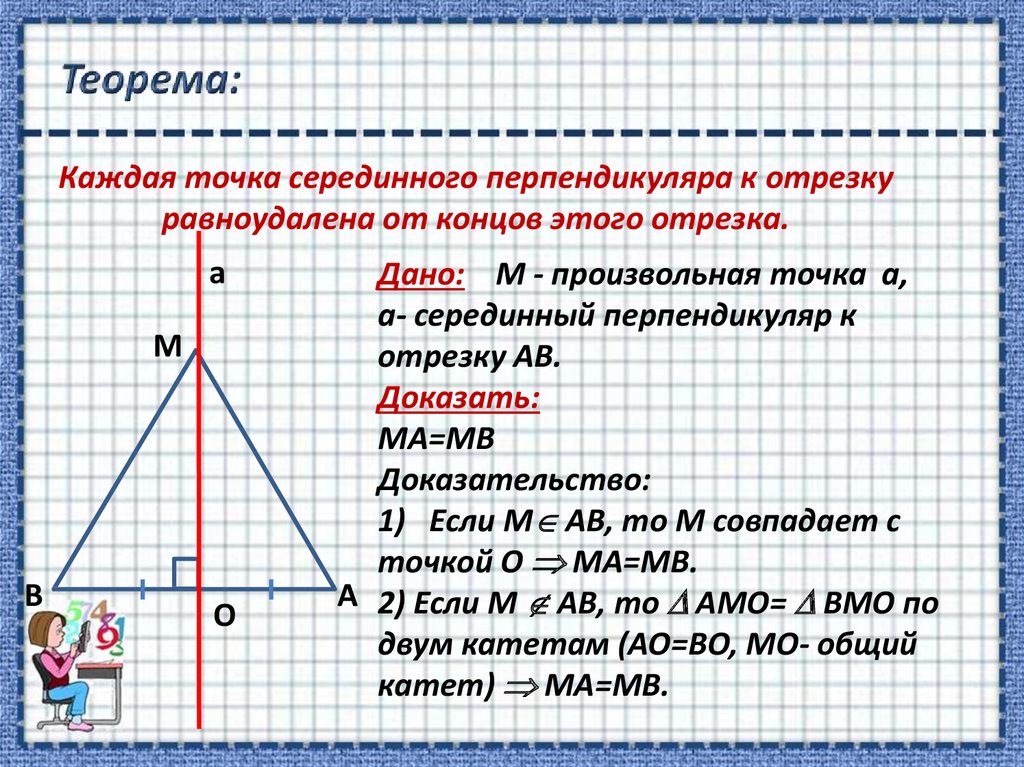
7. Теорема:

Каждая точка серединного перпендикуляра к отрезку
равноудалена от концов этого отрезка.
a
М
B
O
Дано: М - произвольная точка а,
а- серединный перпендикуляр к
отрезку АВ.
Доказать:
МА=МВ
Доказательство:
1) Если М АВ, то М совпадает с
точкой О МА=МВ.
А 2) Если М АВ, то АМО= ВМО по
двум катетам (АО=ВО, МО- общий
катет) МА=МВ.

8.

Обратно: Каждая точка, равноудаленная от концов этого
отрезка, лежит на серединном перпендикуляре к нему.
m
O
А
N
B
Дано:
NА=NВ, прямая m – серединный
перпендикуляр к отрезку АВ.
Доказать: N – лежит на прямой m.
Доказательство:
1)Пусть N АВ, тогда N совпадает с O,
и N лежит на прямой m.
2) Пусть N АВ, тогда:
АNВ – равнобедренный (AN=BN) NO
медиана высота АNВ
NO AB.
3) Через точку О к прямой АВ можно провести
только один серединный перпендикуляр
NO и m совпадают N а.

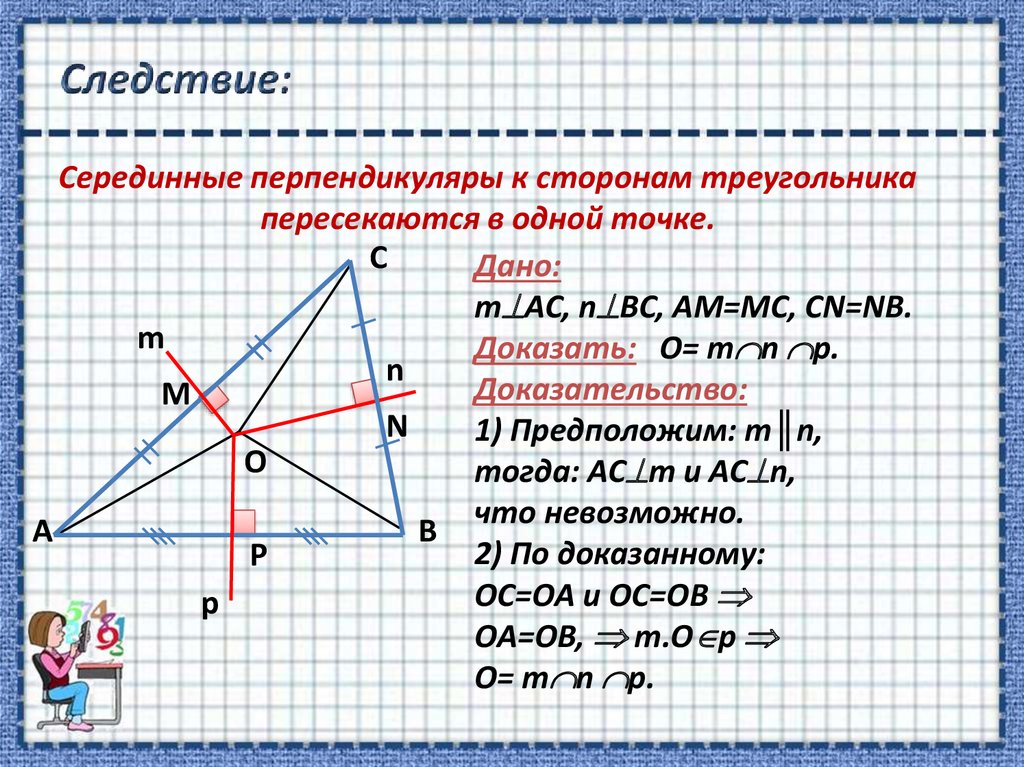
9. Следствие:

Серединные перпендикуляры к сторонам треугольника
пересекаются в одной точке.
С
Дано:
m AC, n BC, AM=MC, CN=NB.
m
Доказать: O= m n p.
n
Доказательство:
М
N
1) Предположим: m║n,
О
тогда: AC m и AC n,
что невозможно.
А
В
2) По доказанному:
P
OC=OA и OC=OB
p
OA=OB, т.O p
O= m n p.

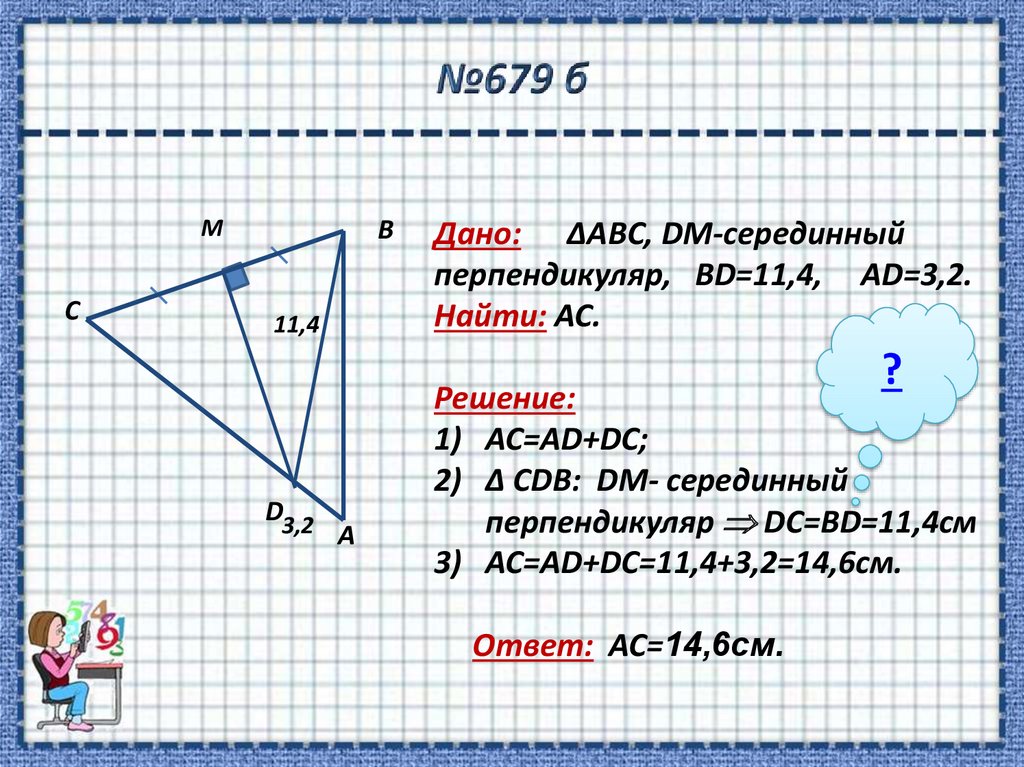
10. №679 б

M
С
B
11,4
Дано: ΔABC, DM-серединный
перпендикуляр, BD=11,4, AD=3,2.
Найти: AC.
?
D3,2
А
Решение:
1) АС=AD+DС;
2) Δ CDB: DM- серединный
перпендикуляр DC=BD=11,4см
3) АС=AD+DС=11,4+3,2=14,6см.
Ответ: АС=14,6см.

11.

Каждая точка серединного
перпендикуляра к отрезку
равноудалена от концов этого
отрезка.

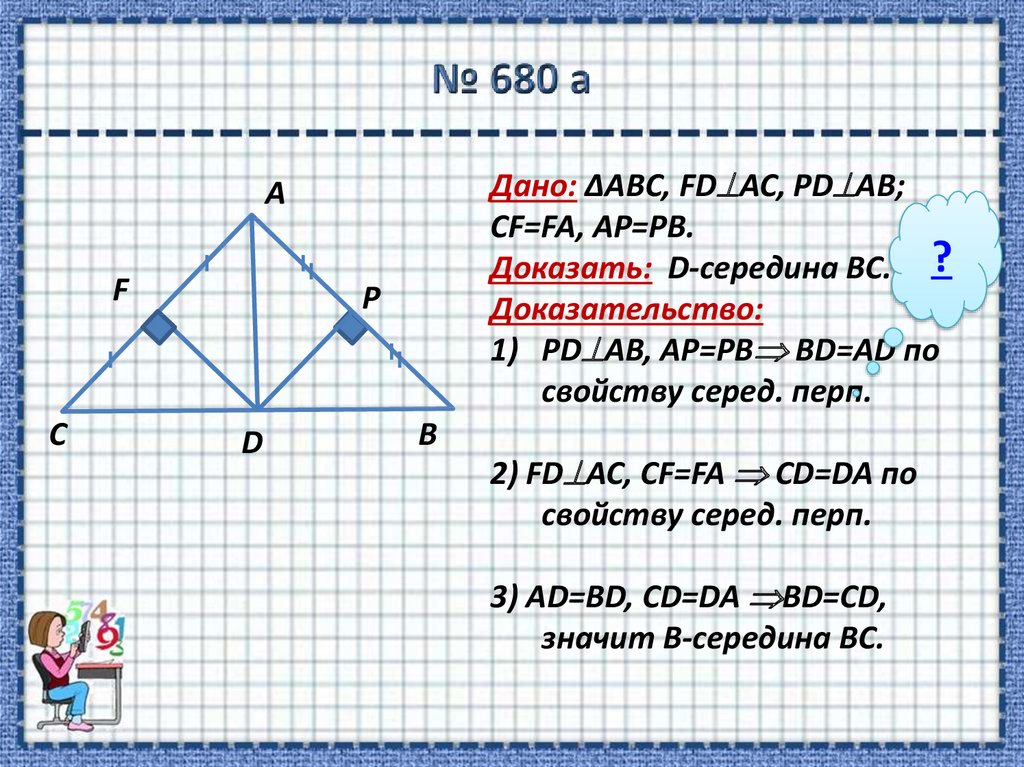
12. № 680 а

Дано: ΔABC, FD AC, PD AB;
CF=FA, AP=PB.
Доказать: D-середина BC. ?
Доказательство:
1) PD AB, AP=PB BD=AD по
свойству серед. перп.
A
F
C
P
D
B
2) FD AC, CF=FA CD=DA по
свойству серед. перп.
3) AD=BD, CD=DA BD=CD,
значит В-середина ВС.

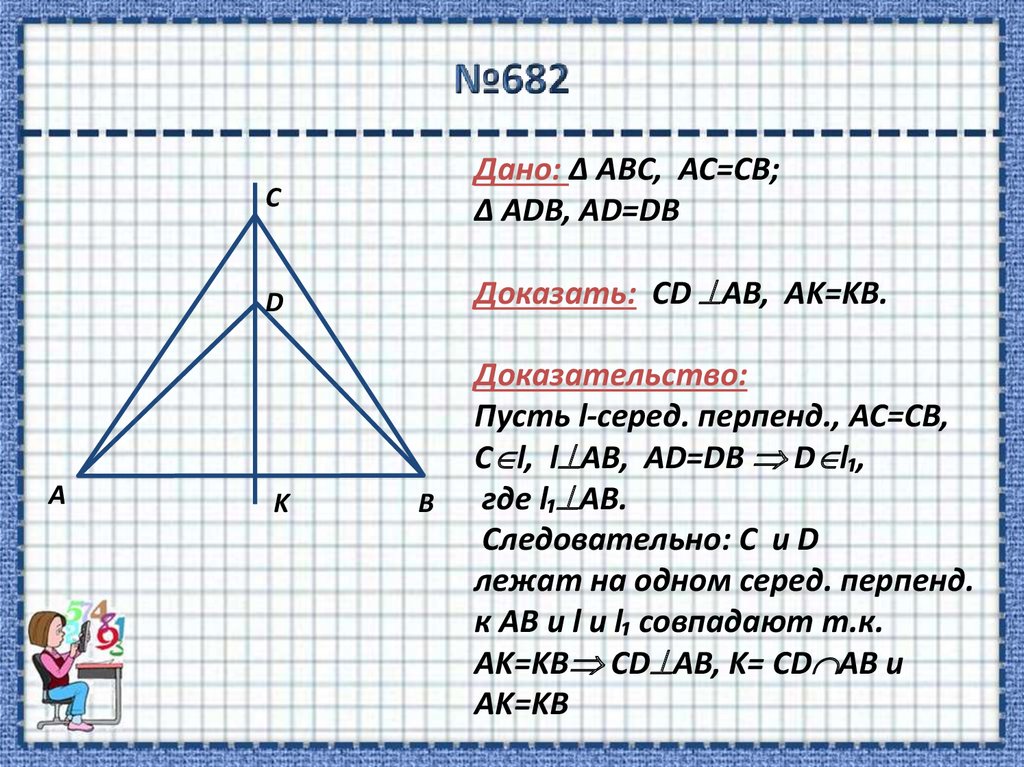
13. №682

A
C
Дано: Δ ABC, AC=CB;
Δ ADB, AD=DB
D
Доказать: CD AB, AK=KB.
K
B
Доказательство:
Пусть l-серед. перпенд., AC=CB,
С l, l AB, AD=DB D l₁,
где l₁ AB.
Следовательно: C и D
лежат на одном серед. перпенд.
к AB и l и l₁ совпадают т.к.
AK=KB CD AB, K= CD AB и
AK=KB

14. Для создания шаблона использовались источники:

Домашнее задание
679 а,б