Разложение вектора по трем некомпланарным векторам

1. Разложение вектора по трем некомпланарным векторам

РАЗЛОЖЕНИЕ ВЕКТОРА
ПО ТРЕМ
НЕКОМПЛАНАРНЫМ
ВЕКТОРАМ
МОБУ «СОШ №78»
учитель математики
Ягодникова Наталья Олеговна

2. Определение компланарных векторов

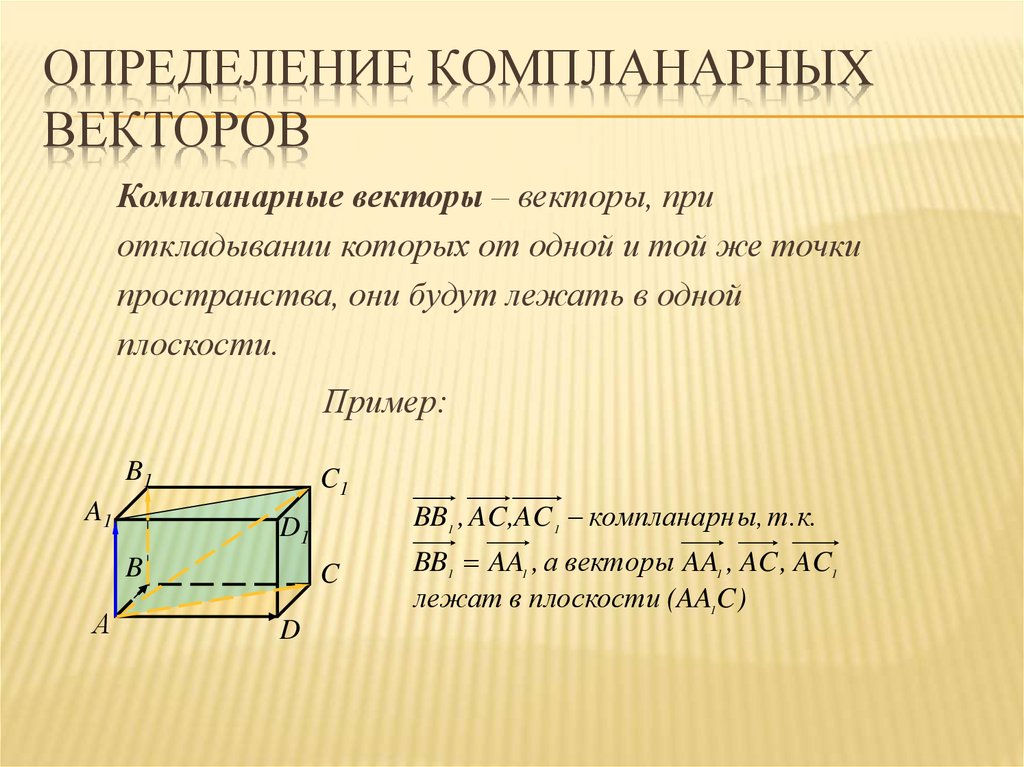
ОПРЕДЕЛЕНИЕ КОМПЛАНАРНЫХ
ВЕКТОРОВ
Компланарные векторы – векторы, при
откладывании которых от одной и той же точки
пространства, они будут лежать в одной
плоскости.
Пример:
B1
A1
C1
D1
B
А
C
D
BB1 , AC,AC 1 компланарн ы, т.к.
BB1 AA1 , а векторы AA1 , AC , AC1
лежат в плоскости (AA1C)

3. Разложение вектора по двум неколлинеарным векторам

РАЗЛОЖЕНИЕ ВЕКТОРА ПО ДВУМ
НЕКОЛЛИНЕАРНЫМ ВЕКТОРАМ
Теорема.
Любой вектор можно разложить по двум
данным неколлинеарным векторам, причем
коэффициенты разложения определяются
единственным образом.

4. Доказательство теоремы

ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ
Дано :
b
a, b неколлинеа рные
векторы
Доказать :
p
a
P
B
p
a
A
p коллинеарен b .
p yb , где y –
1)Пусть
Тогда
некоторое число.
Следовательно,
b
O
p x a yb
Доказатель ство :
A1
p 0 a y b
т.е. p разложен по
векторам a и b .

5. Доказательство теоремы

ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ
2)
pне коллинеарен ни вектору a, ни вектору b.
Отметим О – произвольную точку.
OA a OB b OP p
PA1 BO PA1 OA A1
p OA1 A1 P(пп правилу треугольника)
но : OA1 и A1 P коллинеарн ы a и b соответственно,
значит OA1 x a , A1 P yb ,
следовательно p x a yb , т.е. p разложен по a и b
ч.т.д.

6.

с
b
а
+
+
=

7.

В1
А1
С1
D1
р
В
А
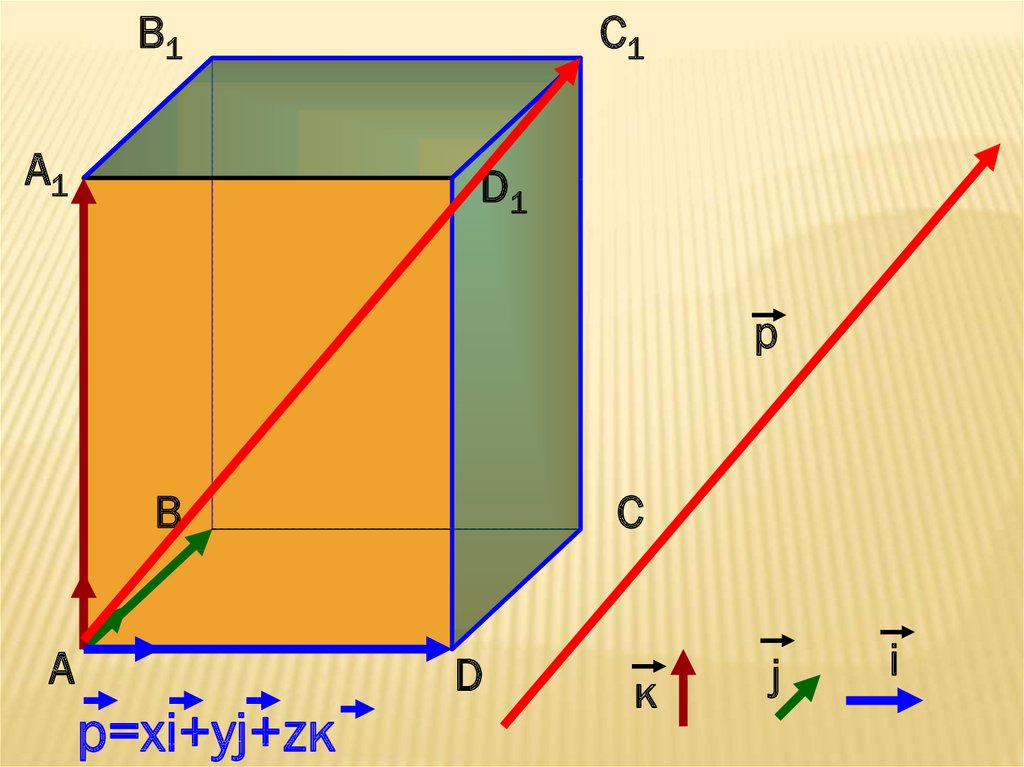
р=xi+уj+zк
С
D
к
j
i

8.

В1
А1
С1
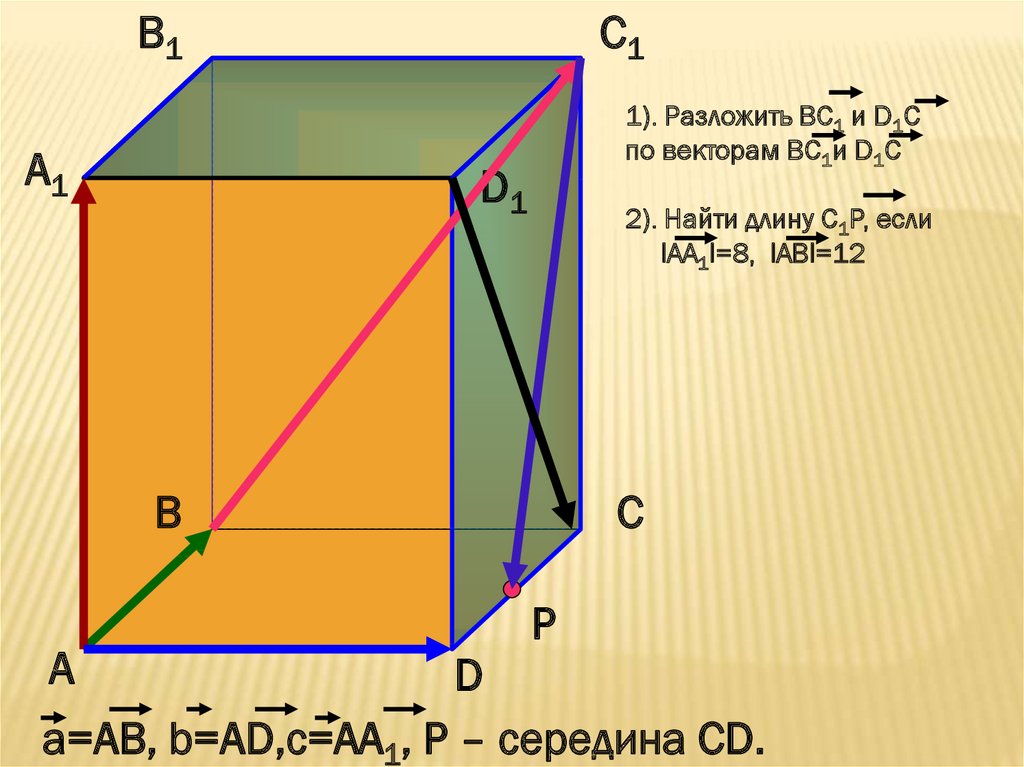
1). Разложить ВС1 и D1С
по векторам ВС1и D1C
D1
2). Найти длину С1Р, если
lАА1l=8, lАВl=12
В
А
С
Р
D
а=АВ, b=АD,с=АА1, Р – середина СD.

9. Разложение вектора по трем некомпланарным векторам

РАЗЛОЖЕНИЕ ВЕКТОРА ПО ТРЕМ
НЕКОМПЛАНАРНЫМ ВЕКТОРАМ
Если вектор p представлен в виде
p xa yb z c
где x, y, z – некоторые числа, то говорят, что вектор
разложен по векторам
,
и .
p
a
b
c
Числа x, y, z называются коэффициентами разложения.
Теорема
Любой вектор можно разложить по трем данным некомпланарным векторам,
причем коэффициенты разложения определяются единственным образом.
Доказательство

10. Доказательство теоремы

ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ
Дано :
b
a, b неколлинеа рные
векторы
Доказать :
p
a
P
B
p
a
A
p коллинеарен b .
p yb , где y –
1)Пусть
Тогда
некоторое число.
Следовательно,
b
O
p x a yb
Доказатель ство :
A1
p 0 a y b
т.е. p разложен по
векторам a и b .

11. Доказательство теоремы

ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ
С
с
P
p
b
O
B
P2
P1
aA
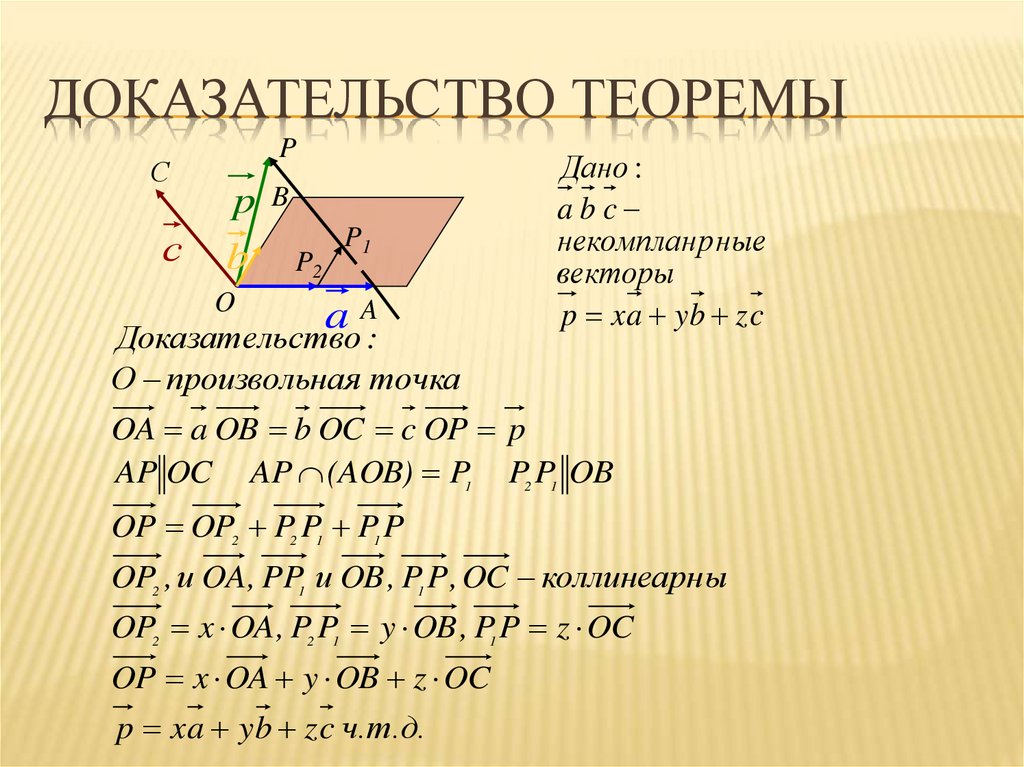
Доказательство :
О произвольн ая точка
Дано :
abc
некомпланр ные
векторы
p x a yb z c
OA a OB b OC c OP p
AP OC AP (AOB) P1 P2 P1 OB
OP OP2 P2 P1 P1 P
OP2 , и OA , PP1 и OB , P1 P , OC коллинеарны
OP2 x OA , P2 P1 y OB , P1 P z OC
OP x OA y OB z OC
p x a yb z c ч.т.д.

12. Вектор, проведенный в центроид треугольника,

ВЕКТОР, ПРОВЕДЕННЫЙ В ЦЕНТРОИД
ТРЕУГОЛЬНИКА,
равен одной трети суммы векторов, проведенных из
этой точки в вершины треугольника.
Центроид – точка пересечения медиан
треугольника.
O
С
A
M
B
1
OM ( OA OB OC )
3
Доказательство

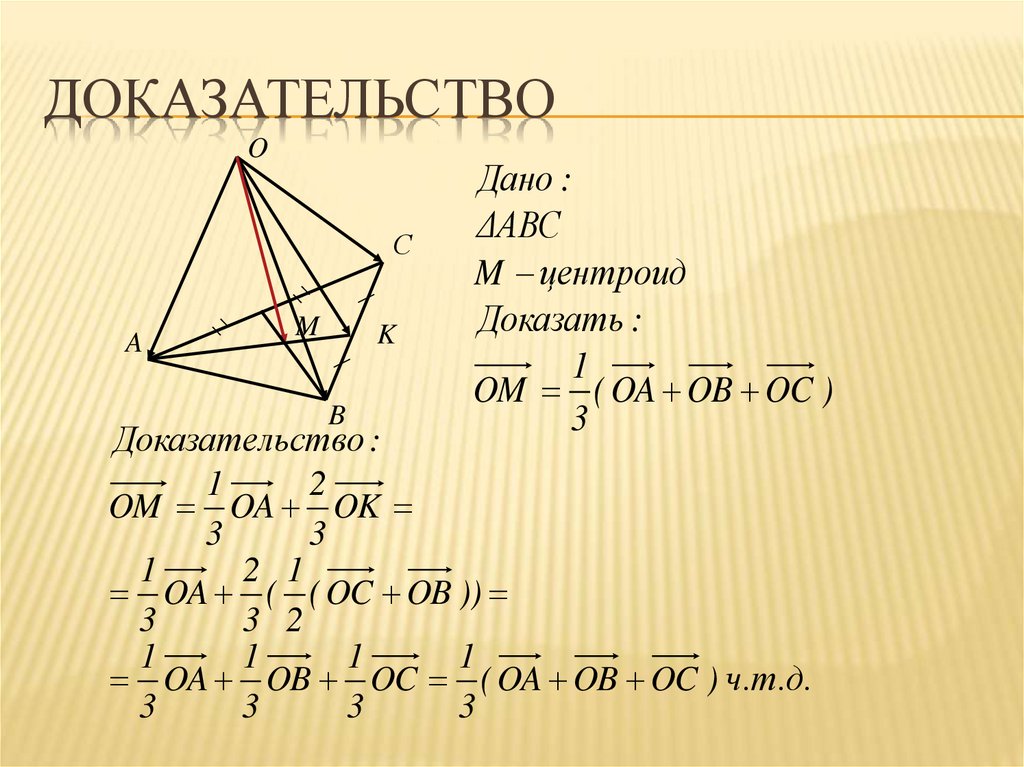
13. Доказательство

ДОКАЗАТЕЛЬСТВО
O
С
A
M
K
B
Дано :
ΔABC
M центроид
Доказать :
1
OM ( OA OB OC )
3
Доказательство :
1
2
OM OA OK
3
3
1
2 1
OA ( ( OC OB ))
3
3 2
1
1
1
1
OA OB OC ( OA OB OC ) ч.т.д.
3
3
3
3

14. Вектор, проведенный в точку пересечения диагоналей параллелограмма,

ВЕКТОР, ПРОВЕДЕННЫЙ В ТОЧКУ
ПЕРЕСЕЧЕНИЯ ДИАГОНАЛЕЙ
ПАРАЛЛЕЛОГРАММА,
равен одной четверти суммы векторов, проведенных
из этой точки в вершины параллелограмма.
O
C
B
M
A
D
1
OM ( OA OB OC OD )
4
Доказательство

15. Доказательство

ДОКАЗАТЕЛЬСТВО
O
B
C
M
Дано :
ABCD пар м
BD AC M
Доказать :
1
OM ( OA OB OC OD )
4
A
D
1
OM ( OA OC )
2
1
OM ( OB OD )
2
1
1
1
1
2OM OA OB OC OD
2
2
2
2
1
1
1
1
OM OA OB OC OD
4
4
4
4
1
( OA OB OC OD ) ÷.ò.ä.
4

16. Вектор, лежащий на диагонали параллелепипеда,

ВЕКТОР, ЛЕЖАЩИЙ НА ДИАГОНАЛИ
ПАРАЛЛЕЛЕПИПЕДА,
равен сумме векторов, лежащих на трех его ребрах,
исходящих из одной вершины.
B1
C1
A1
a
A
d
D1
B
C
b
с
D
d a b c
Доказательство

17. Доказательство

ДОКАЗАТЕЛЬСТВО
Дано :
B1
C1
A1
a
A
d
AA1 a
D1
B
C
b
с
D
Доказательство :
AC1 AA1 AB1 BC1
AA1 AB AD
a b c ч.т.д.
ABCDA1B1C1D1 пар м
AB b
AD c
AC1 d
Доказать :
d a b c