Системы координат при моделировании ионной имплантации

1. Моделирование технологических процессов

Лекция 2

2. Вопросы к экзамену

1.
2.
3.
4.
5.
6.
Системы координат при моделировании ионной
имплантации.
Принцип суперпозиции при расчете функций
распределения примеси.
Аналитические аппроксимации распределения
ионов. Функции Гаусса.
Аналитические аппроксимации распределения
ионов. Распределение Пирсона-IV.
Аналитические аппроксимации распределения
ионов, учитывающие эффект каналирования.
Особенности моделирования ионной имплантации в
многослойных мишенях.
2

3. Системы координат при моделировании ионной имплантации

Первая система координат – это система, привязанная к
реальной установке ионной имплантации. В этой системе
координат ионный пучок всегда направлен вдоль оси –Z.
• Вторая система координат – это система, привязанная к
подложке. В этой системе всегда ось X направлена вдоль
базового среза пластины, ось Z – перпендикулярно
поверхности подложки. Ось Y образует с заданными
осями X и Z правую тройку
• Третья система координат – это система, построенная
непосредственно для проведения вычислений и
моделирования либо двумерного сечения в двумерных
задачах, либо трехмерного кристалла в трехмерных
задачах
3

4. Система координат подложки

Tilt = 0 и Rotation = 0
Положение
пластины в
установке ионной
имплантации и
связь первой и
второй
координатных
систем определяется
параметрами Tilt и
Rotation.
Третья система координат
определяется через
положение секущей в
системе координат
подложки. Положение
секущей задается
координатами начала (x0,
y0) и конца (x1, y1)
вектора секущей на
поверхности подложки в
операторе Cutline (x0, y0,
x1, y1).
Cutline (0, 0, 1, 0)
4

5. Стандартное положение подложки Tilt=7º, Rotation= - 90º

Наклон подложки - вращение вокруг направления базового среза задается углом Tilt
Поворот описывается, как вращение вокруг оси Z подложки и задается углом
Rotation
5

6. Определение углов Tilt и Rotation

Угол Tilt может быть определен как угол между осями Z в первой и
второй системах координат, т.е. между осями Z имплантера и подложки.
Угол Rotation определяется как угол между проекцией оси Z имплантера
на плоскость подложки и осью Y подложки. Положительным считается
направление против часовой стрелки
6

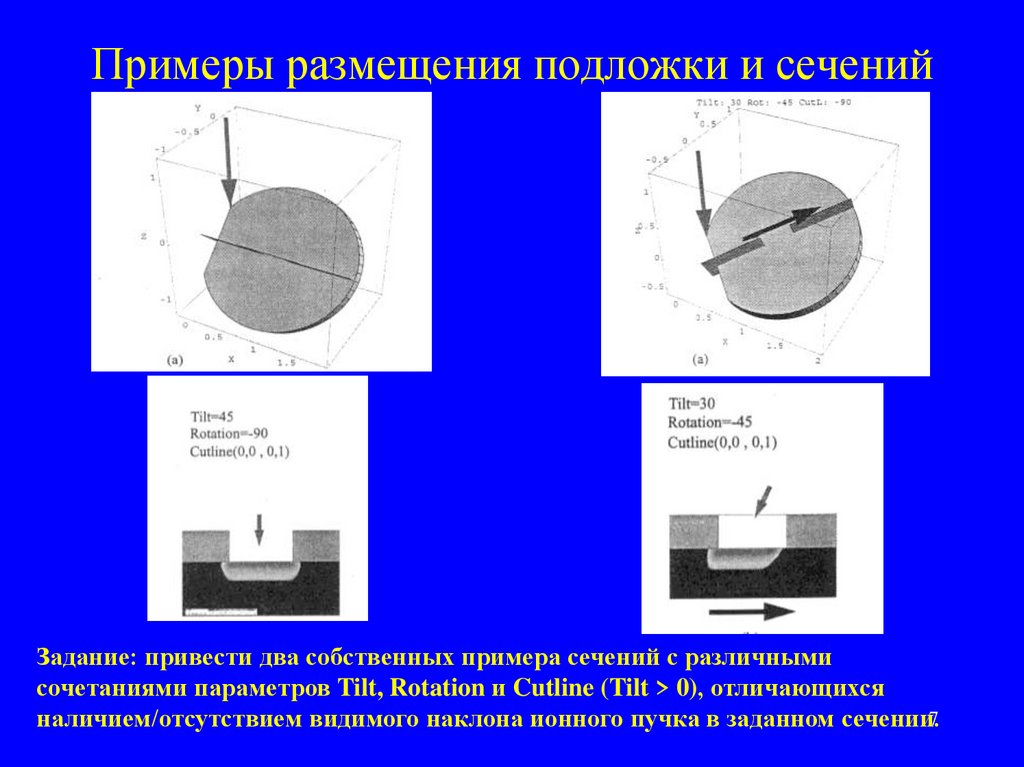
7. Примеры размещения подложки и сечений

Задание: привести два собственных примера сечений с различными
сочетаниями параметров Tilt, Rotation и Cutline (Tilt > 0), отличающихся
наличием/отсутствием видимого наклона ионного пучка в заданном сечении.7

8. Принцип суперпозиции при расчете функций распределения примеси

Во время имплантации ионы внедряются в подложку через открытые
участки внешней поверхности и рассеиваются внутри подложки в трех
измерениях. Проекция ионного пучка в двумерной плоскости
моделирования зависит от углов поворота и наклона подложки и может
приводить к несимметричным профилям распределения примеси в
окрестностях краев маски.
Предположим, что ионный пучок, падающий в точку внешней
границы с координатами (ξ, η) создает в подложке функцию
распределения Φ(x, y, ξ, η). Тогда в любой точке (x, y) внутри подложки
концентрация примеси будет вычисляться как суперпозиция функций
распределения, исходящих от всех точек падения ионного пучка, т.е. от
всех точек внешней границы структуры:
N ( x, y)
( x, y, (s), (s))ds
Sout
8

9. Распределение примеси вблизи краев маски

Для того чтобы сравнивать концентрацию имплантированных ионов с
экспериментальными одномерными ВИМС – профилями, двумерный
профиль представляется как произведение двух ортогональных
функций: основной функции fp(x) и латеральной функции fl(y):
9

10. Аналитические аппроксимации распределения ионов. Функция Гаусса

В соответствии с классической теорией ЛШШ и
диффузионной моделью Бирсака профили
имплантированных ионов должны описываться
гауссовскими распределениями. Аппроксимация
распределения ионов по нормальному закону распределение Гаусса является симметричным
распределением и характеризуется двумя параметрами:
N(x) =
x RP 2
1 D
exp
2
2
2 P
P
где D – доза имплантированной примеси, см-2,
RP средняя проекция пробега ионов и
среднеквадратичное отклонение проекции пробега
P
10

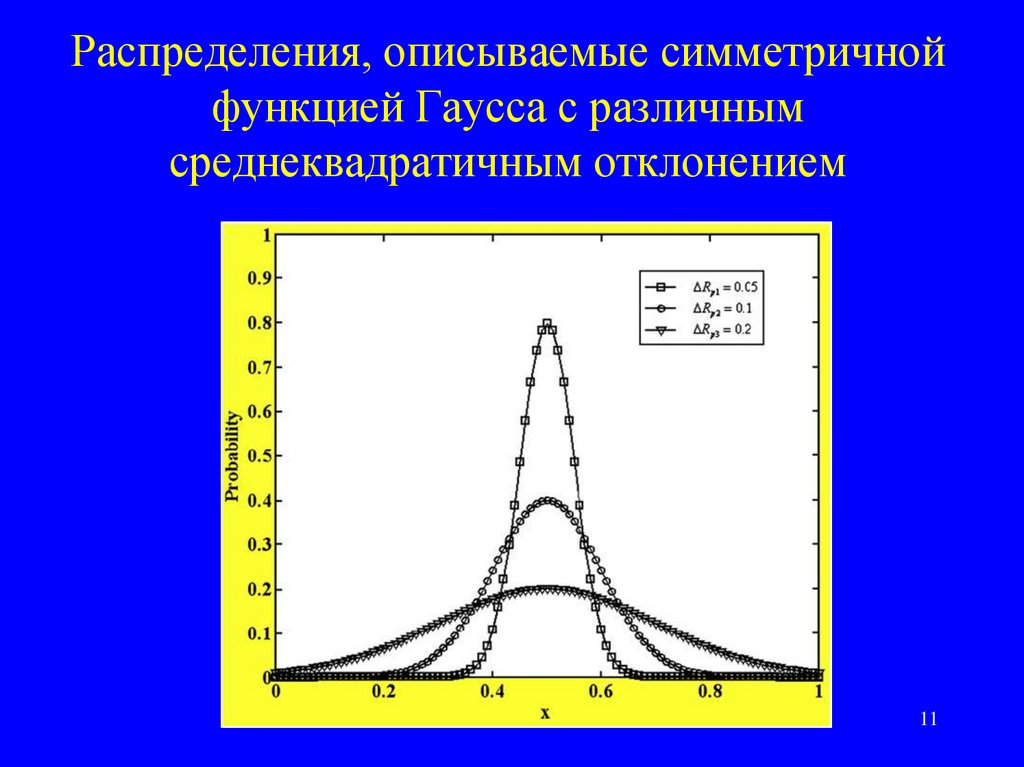
11. Распределения, описываемые симметричной функцией Гаусса с различным среднеквадратичным отклонением

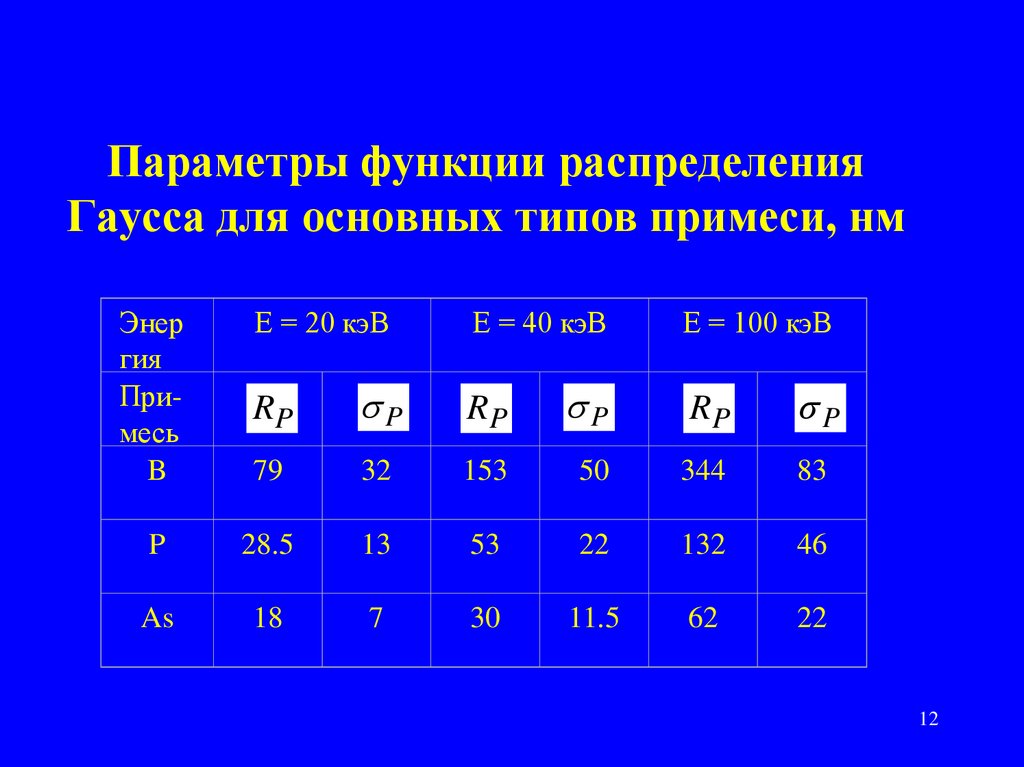
11

12. Параметры функции распределения Гаусса для основных типов примеси, нм

Энер
гия
Примесь
B
E = 20 кэВ
E = 40 кэВ
E = 100 кэВ
RP
P
RP
P
RP
P
79
32
153
50
344
83
P
28.5
13
53
22
132
46
As
18
7
30
11.5
62
22
12

13. Двойное сопряженное распределение Гаусса (асимметричное)

( x RP ) 2
D n0 exp
, при
2
2 P
( x RP ) 2
N(x) =
, при
D n0 exp
2
2 P 2
1
n0
=
RP
erf
P
P2
2
2
P
erf ( z )
2
z
e
y2
dy
≈
x RP
x RP
2
P P 2
функция ошибок
0
13

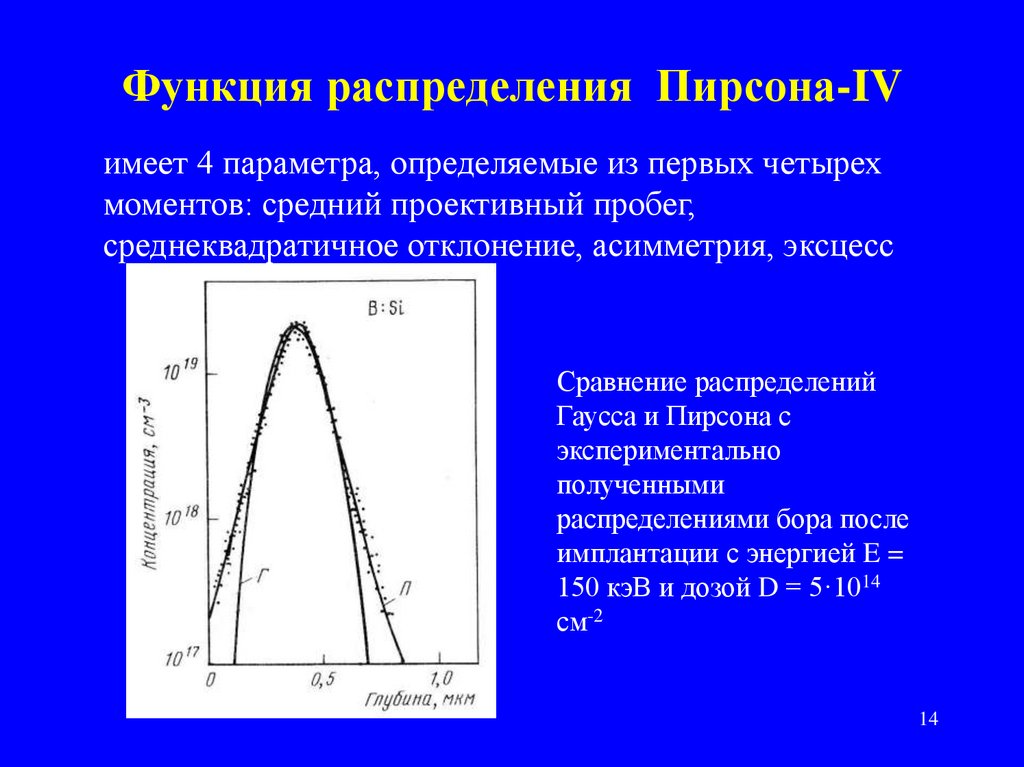
14. Функция распределения Пирсона-IV

имеет 4 параметра, определяемые из первых четырех
моментов: средний проективный пробег,
среднеквадратичное отклонение, асимметрия, эксцесс
Сравнение распределений
Гаусса и Пирсона с
экспериментально
полученными
распределениями бора после
имплантации с энергией E =
150 кэВ и дозой D = 5·1014
см-2
14

15.

Функция распределения Пирсона-IV является
решением дифференциального уравнения
d
z a
f ( z)
f ( z)
2
dz
b0 b1 z b2 z
z x RP
где
N(x) = D b2 x RP
2
b b 2a
2b2 x RP b1
1
2
b1 x RP b0 exp
arctg
2
2
4b2b0 b1
4b2b0 b1
a b1 P 3 A
b0 P2 4 3 2 A
b2 2 3 2 6 A
A 10 12 2 18
15

16. Параметры функции распределения Пирсона-IV

RP = μ1 =
xf ( x)dx
– средний проективный пробег, он же
1-ый момент функции распределения;
среднеквадратичное отклонение 3 P3
x RP
3
N ( x) dx D P3
σP = (μ2)1/2
- асимметрия
эксцесс, характеризует плавность
вблизи вершины -
где
i
4 P4
x RP
4
N ( x) dx D P4
( x RP )
i
f ( x)dx
- i-ый момент функции распределения
16

17. Асимметрия γ функции распределения Пирсона-IV

При γ = 0:
максимум распределения Пирсона лежит в
точке RMAX = RP ,
NMAX = N(RP);
При γ < 0:
пик находится глубже RP (RMAX > RP) и кривая
распределения справа от максимума падает
быстрее, чем слева.
При γ > 0:
верно обратное утверждение (RMAX < RP)
17

18. Аналитические аппроксимации распределения ионов, учитывающие сильную асимметрию и эффект каналирования

18

19. Распределение Гаусса с обобщенным экспоненциальным «хвостом»

N(x) =
( x RP ) 2
1 n0
D
exp
, при x R P P
2
2 P
2 P
2
(
x
R
)
x
R
1
1
P
P ,
D
n
exp
exp
0
2
l
2
2
2 P
exp
P
P
при x RP P ;
D – доза имплантированной примеси, 1/ см-3,
RP - средняя проекция пробега ионов
P - среднеквадратичное отклонение проекции пробега
k – коэффициент, обеспечивающий непрерывность в точке x = RP + P
n0 – обратное значение нормы функции распределения,
α, lexp – параметры распределения в «хвостовой» части.
19

20. Распределение Пирсона -IV с линейно- экспоненциальным хвостом

Распределение Пирсона -IV с линейноэкспоненциальным хвостом
N P x ,
N(x) = N T x ,
N x ,
l
0 x x max
x max x x a
xa x
NP(x) - распределение Пирсона –IV
NT(x) - функция распределения в
переходной области
Nl(x) - функция распределения в
«хвостовой» части
xmax - координата максимума функции распределения
Пирсона
N max N P xmax
xa - координата точки, в которой концентрация примеси
равна половине максимального значения
N a N P xa
1
N max
2
Функция распределения в «хвостовой» части
x xmax
N l x N P x
lexp
N P xmax exp x xmax
lexp
20

21. Распределение Пирсона -IV с линейно- экспоненциальным хвостом в переходной области

Распределение Пирсона -IV с линейноэкспоненциальным хвостом в переходной области
N T x N P xmax exp A x xmax 2 B x xmax 3
А и В определяются из условий непрерывности функции и
производной в точке x = xa:
N l xa NT xa
d
d
N l x
N T x N a
dx
dx
3 ln N a N max
N a
A
2
N a xmax xa
xmax xa
B
2 ln N a N max
N a
xmax xa 3 N a xmax xa 2
21

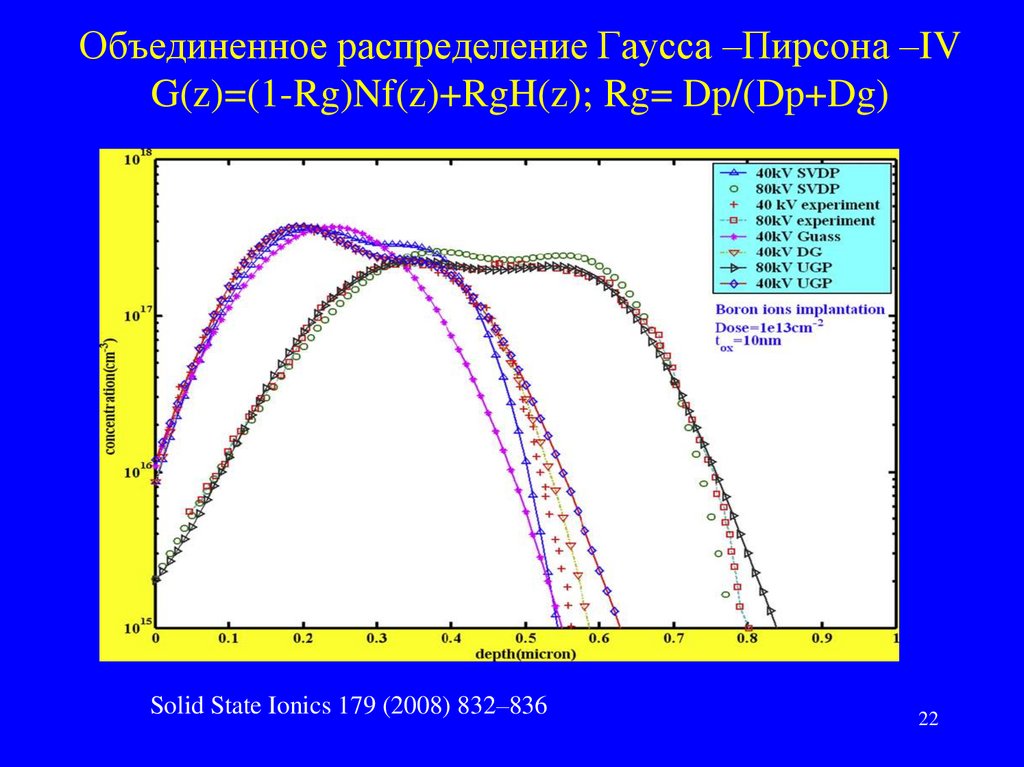
22. Объединенное распределение Гаусса –Пирсона –IV G(z)=(1-Rg)Nf(z)+RgH(z); Rg= Dp/(Dp+Dg)

Solid State Ionics 179 (2008) 832–836
22

23. Латеральное распределение примеси

f(x,y) =
2
x
1
exp
2
2
(
y
)
2 L ( y )
L
Латеральное распределение описывается
функцией Гаусса со среднеквадратичным
отклонением, зависящим от глубины
Зависимость от глубины может быть описана
с помощью вектора пяти параметров (p1…p5).
23

24. Распределение постимплантационных дефектов

Для описания распределения постимплантационных дефектов так же,
как для распределения примеси используются две ортогональные
функции
Основная функция может быть трех типов:
Простая функция Гаусса
Для легких ионов примеси с экспоненциальным хвостом,
направленным к поверхности подложки
Для тяжелых ионов с экспоненциальным хвостом,
направленным вглубь подложки
Для латерального распределения постимплантационных дефектов
используются те же функции, что и для латерального распределения
примеси со среднеквадратичным отклонением, зависящим от глубины
24

25. Функции распределения постимплантационных дефектов

x R 2
P
fP(x) = NFP k·exp
2
2 P
P
N FP k1 exp( x ),
x
x
R
0
P
l
l
fP(x)=
( x RP )2
N k exp( 2 2 ),
x x0
FP 2
P
2
для легких ионов
N FP k2 exp( ( x RP2 ) ), x x0
2 P
fP(x)=
x x0
N FP k1 exp( xl ),
2
для тяжелых ионов
NFP – число Френкелевских дефектов на ион, k, -k1, k2 - нормирующие
множители
25

26. Распределение примеси в многослойных мишенях

Если имплантация осуществляется в многослойную
структуру, содержащую слои различных материалов,
функции распределения примеси должны корректироваться
с учетом эффективности торможения в вышележащих
слоях.
Используется два подхода:
-
коррекция параметров функции распределения;
-
коррекция дозы.
26

27. Коррекция параметров функции распределения

При коррекции параметров распределения различие в
тормозной способности слоев оценивается по
отношению значений среднего проективного пробега в
различных материалах.
Рассчитывается сдвиг профиля в i-ом слое
RPi
i t j 1
R
j 1
Pj
j i
где tj = dj – dj-1 – толщина j-го слоя
27

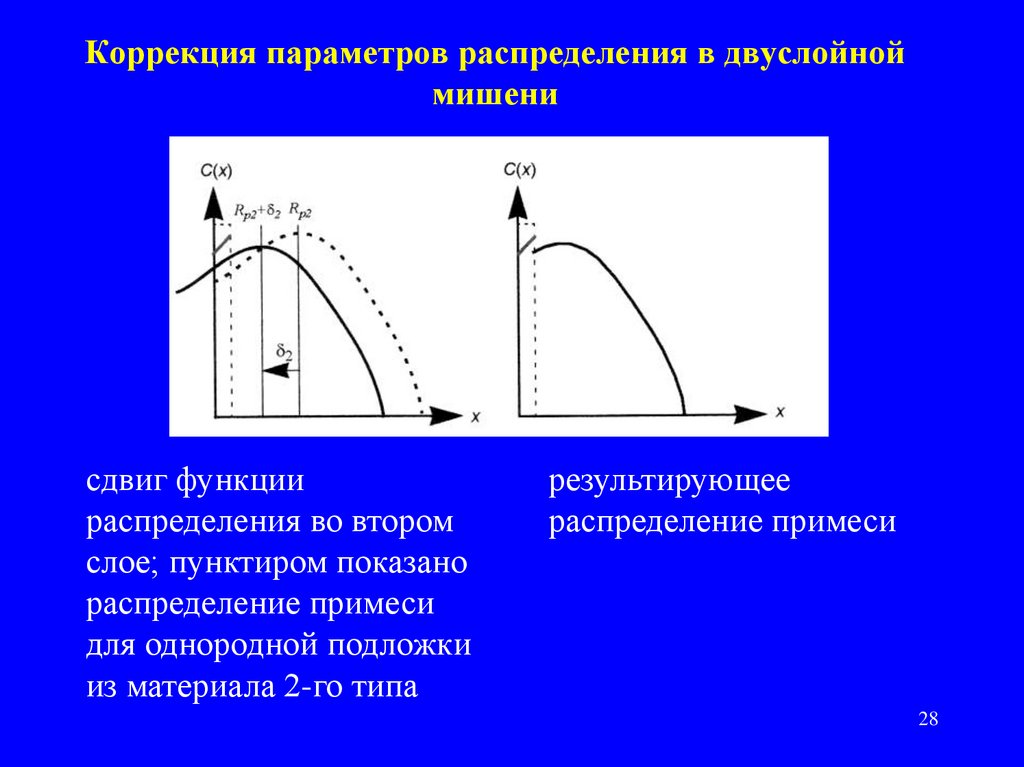
28. Коррекция параметров распределения в двуслойной мишени

сдвиг функции
распределения во втором
слое; пунктиром показано
распределение примеси
для однородной подложки
из материала 2-го типа
результирующее
распределение примеси
28

29. Коррекция дозы

При коррекции дозы сдвиг профиля вычисляется,
исходя из дозы, поглощенной вышележащими
слоями:
i di d eff
deff
Deff
f P ( x)dx
0
di – положение верхнего края i-го слоя
29

30. Сдвиг профиля при имплантации в двухслойную мишень

для функции
распределения Гаусса
доза, поглощенная в
первом слое равна
D1
RP 2 d eff
RP1 d1 D
D
1
erf
1
erf
2
2 P1 2
2 P 2
y
erf ( y )
2
e
z2
dz
- интеграл вероятности
0
Находим сдвиг функции распределения по поглощенной эффективной дозе:
RP1 d1 RP 2 d eff
2 P1 2 P 2
d eff RP 2 ( RP1 d1 )
RPeff2 RP 2 (d eff d1 ) ( RP1 d1 )
P2
d1
P1
P2
P1

31. Моделирование распыления мишени

При анализе ионной имплантации эффектом распыления обычно
пренебрегают. Однако его следует учитывать, когда имплантация
производится высокой дозой ионов с низкой энергией, что необходимо
для формирования мелкозалегающих p-n переходов. Основным
параметром процесса распыления является коэффициент распыления
S, численно равный количеству атомов подложки, выбиваемых с
поверхности ионом примеси. При направлении ионного пучка
нормальном к поверхности коэффициент распыления равен
3 Sn ( E ) ( M 2 / М1 )
S
4
2С0U 0
Sn(E) – ядерная тормозная
способность,
( M 2 / М1 )
- численно
определяемая функция, U0 –
поверхностная энергия связи,
U0 = 7.81 для кремния, C0 –
константа
31

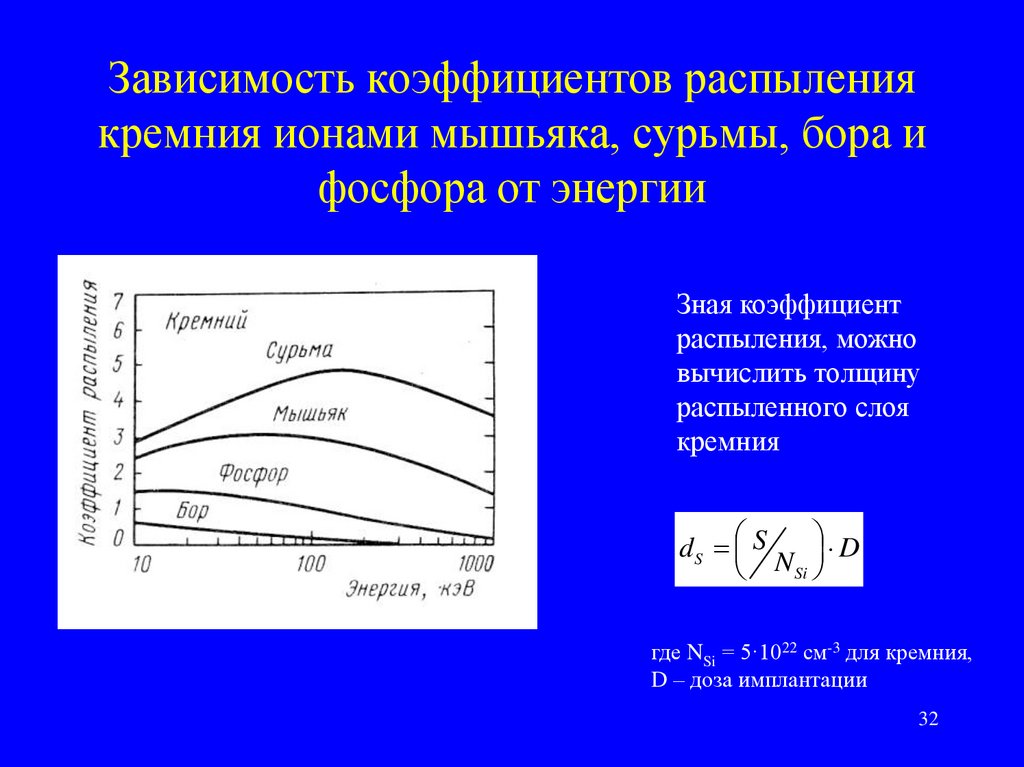
32. Зависимость коэффициентов распыления кремния ионами мышьяка, сурьмы, бора и фосфора от энергии

Зная коэффициент
распыления, можно
вычислить толщину
распыленного слоя
кремния
D
d S S
N Si
где NSi = 5·1022 см-3 для кремния,
D – доза имплантации
32