Уравнение сферы. Уравнение плоскости и прямой

1.

1.
2.
Понятие сферы и её элементов
Уравнение сферы в заданной
системе координат

2.

3.

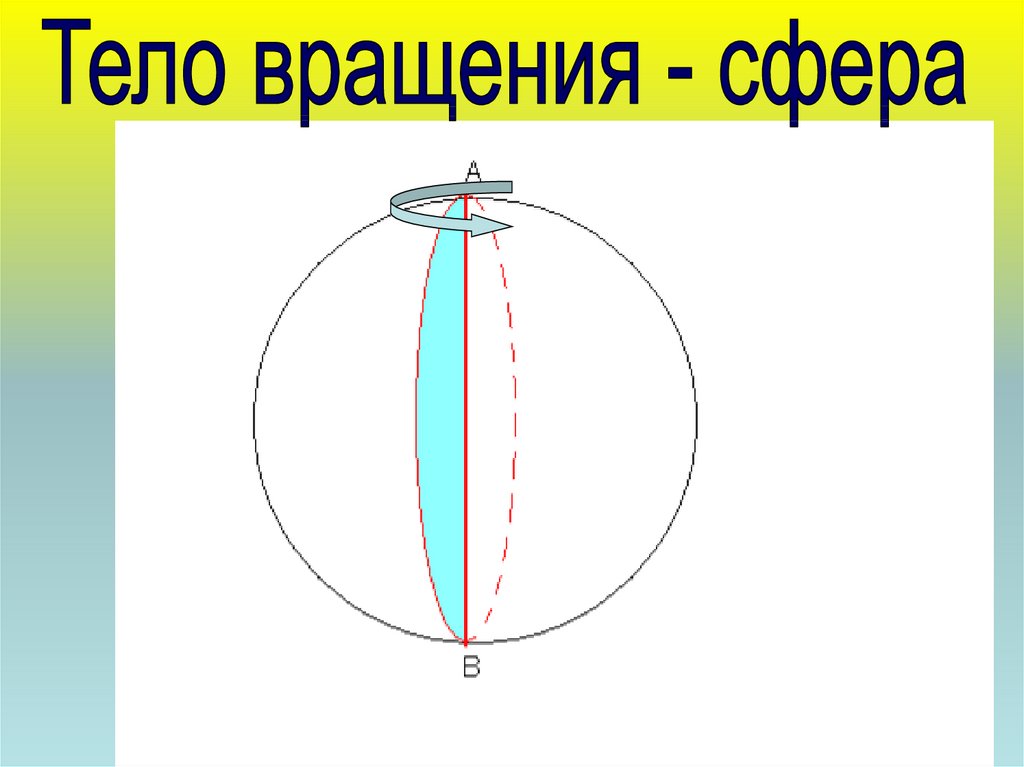
• Сферой называется
поверхность, состоящая из
всех точек пространства,
расположенных на данном
расстоянии от данной точки.
• т.О - центр сферы
• ОА – радиус сферы.
• Любой отрезок,
соединяющий центр и
какую-нибудь точку
сферы называется
радиусом сферы.
• ВС – диаметр сферы.
• Отрезок, соединяющий
две точки сферы и
проходящий через ее
центр, называется
диаметром сферы
• d=2r

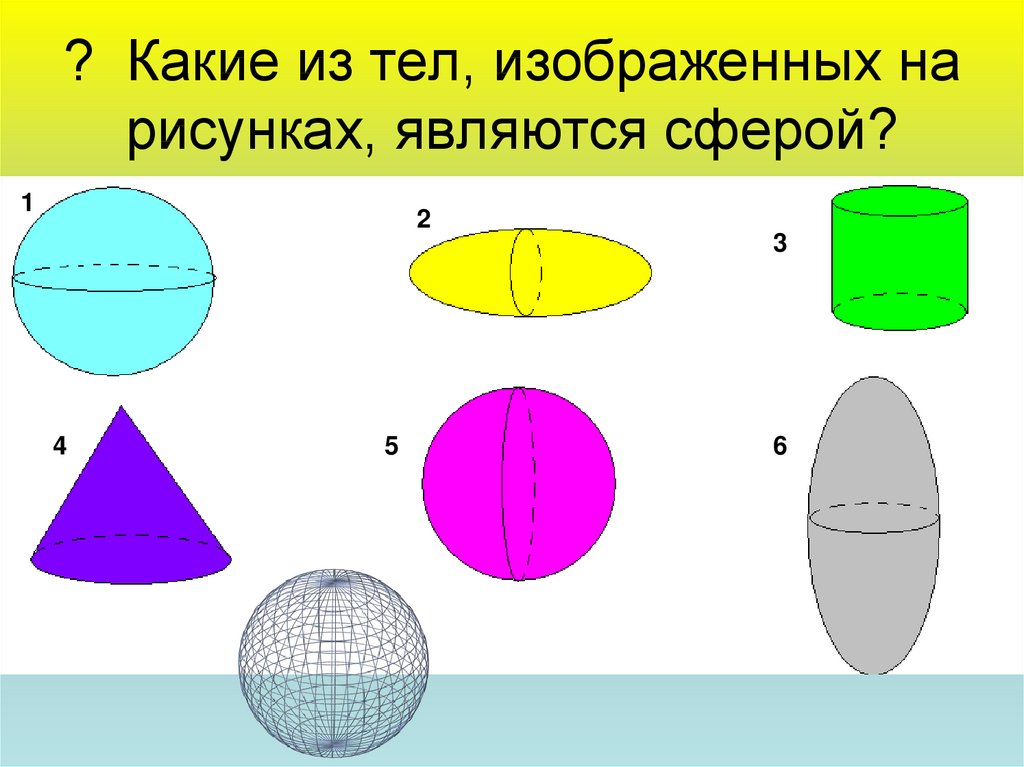
4. ? Какие из тел, изображенных на рисунках, являются сферой?

1
2
3
4
5
6

5.

z
у
• М(х;у;z)
М(х;у)
у
L
х
Х
L
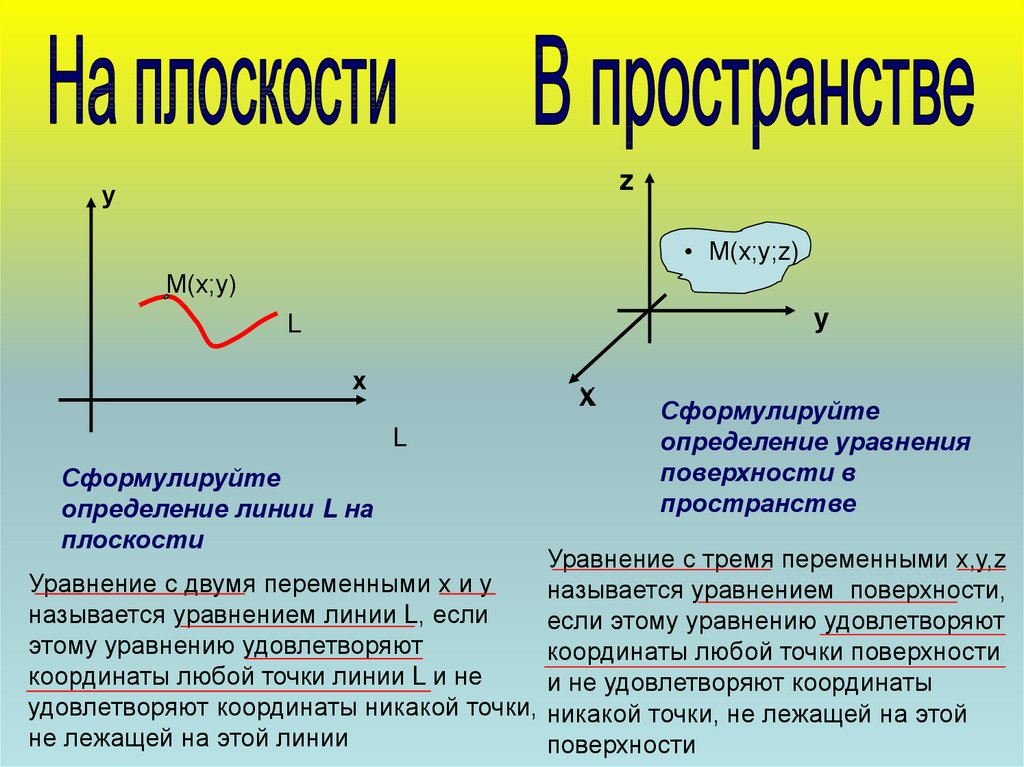
Сформулируйте
определение линии L на
плоскости
Сформулируйте
определение уравнения
поверхности в
пространстве
Уравнение с тремя переменными х,у,z
Уравнение с двумя переменными х и у
называется уравнением поверхности,
называется уравнением линии L, если
если этому уравнению удовлетворяют
этому уравнению удовлетворяют
координаты любой точки поверхности
координаты любой точки линии L и не
и не удовлетворяют координаты
удовлетворяют координаты никакой точки, никакой точки, не лежащей на этой
не лежащей на этой линии
поверхности

6.

у
z
(х;у;z)
М(х;у)
С
х
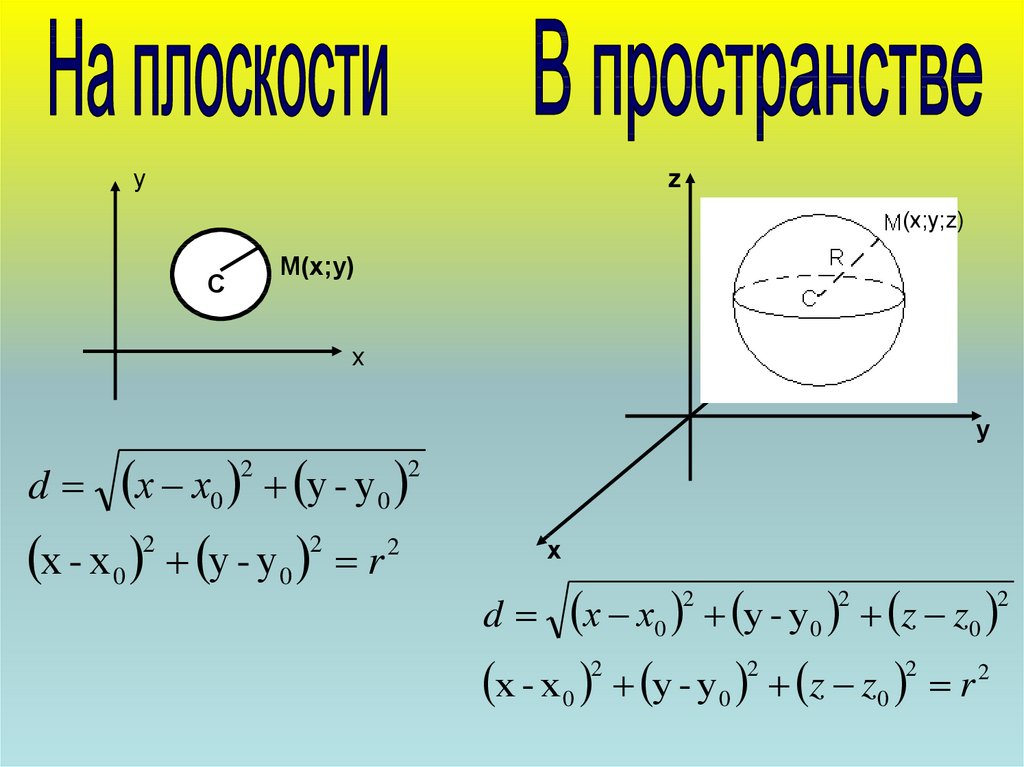
х х0 у - у0
2
2
х - х 0 у - у0 r 2
d
2
у
2
х
2
2
2
d х х0 у - у 0 z z0
2
2
2
х - х 0 у - у0 z z0 r 2

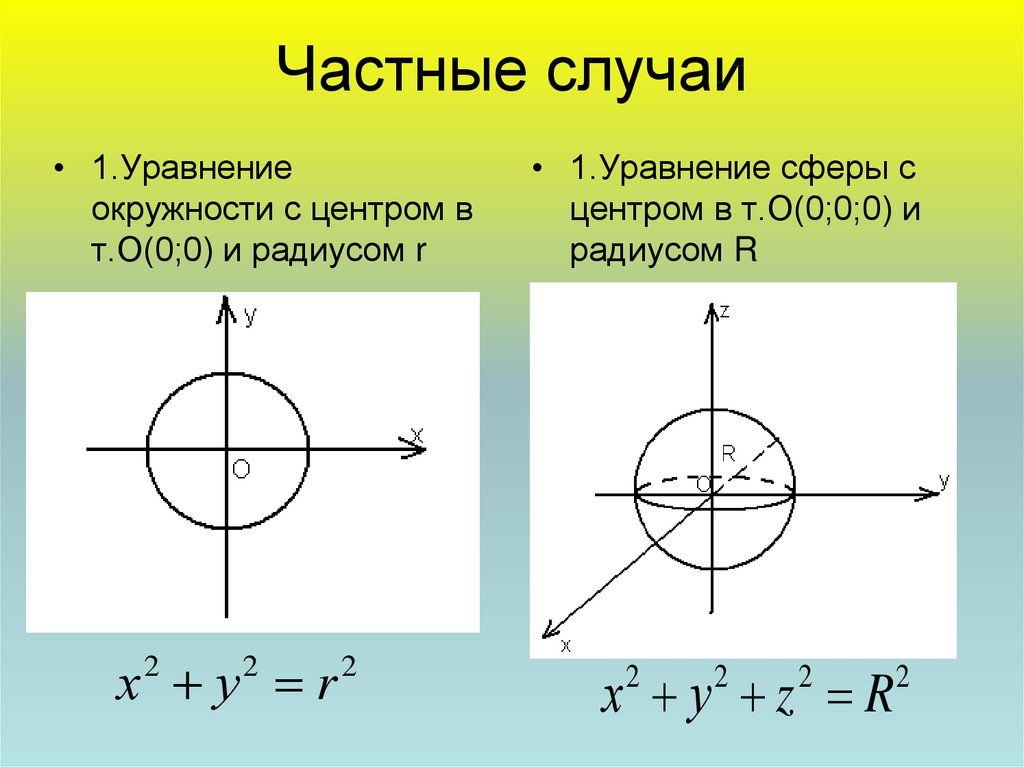
7. Частные случаи

• 1.Уравнение
окружности с центром в
т.О(0;0) и радиусом r
х у r
2
2
2
• 1.Уравнение сферы с
центром в т.О(0;0;0) и
радиусом R
х у z R
2
2
2
2

8. Выбрать из предложенных уравнений – уравнение сферы:

1.
2.
3.
4.
5.
6.
7.
8.
( х 1) 2 ( у 2) 2 4
( х 1)2 ( у 5)2 ( z 3)2 22
2х 3у 6
( х 2)2 ( у 4)2 ( z 8) 2 9
2 х 2 5х 3 0
х 2 у 2 z 2 16
( х 2) 2 ( у 4) 2 ( z 7) 2 9
х2 4х у 2 z 2 0
1.Ур-е окружности
2.Ур-е сферы
3.Ур-е прямой
4.Ур-е сферы
5.Ур-е параболы
6.Ур-е сферы
7.Ур-е сферы
8. ?

9. В данных уравнениях определите координаты центра сферы и радиус

• 1.
( х 2) ( у 4) z 7 9
• 2.
( х 6) ( у 0,5) z 5
• 3.
х у ( z 1) 6
• 4.
х у z 49
2
2
2
2
2
2
2
2
2
2
2
2

10.

Составьте уравнение сферы по
следующим данным центра и радиуса
сферы:
1.Дано: С(-2;8;1);
R=11
2.Дано: А(3;-2;0);
R=0,7
3.Дано: О(0;0;0);
R=1
Проверяем ответы:
х 2 у 8 z 1 121
2
2
2
х 3 у 2 z 0,49
2
2
х у z 1
2
2
2
2

11. Задача

• Определить принадлежит ли т.А
сфере, заданной уравнением
( х 3) ( у 7) ( z 5) 30
2
2
2
если: а) т.А(5;-2;6)
б) т.А(-5;2;6)
5 3
2
Решение:
2 7 6 5 30
2
2
5 3 2 7 6 5
2
2
2
30
Равенство верное,
следовательно А(5;-2;6)
принадлежит сфере
Равенство неверное,
следовательно А(5;-2;6)
не принадлежит сфере

12.

13. Общее уравнение плоскости

14. Особые случаи уравнения:

15. Особые случаи уравнения:

16. Особые случаи уравнения:

17. Уравнения координатных плоскостей

18. Две плоскости в пространстве:

совпадают, если
существует такое
число k, что
параллельны,
если существует
такое число k, что
В остальных случаях плоскости пересекаются.

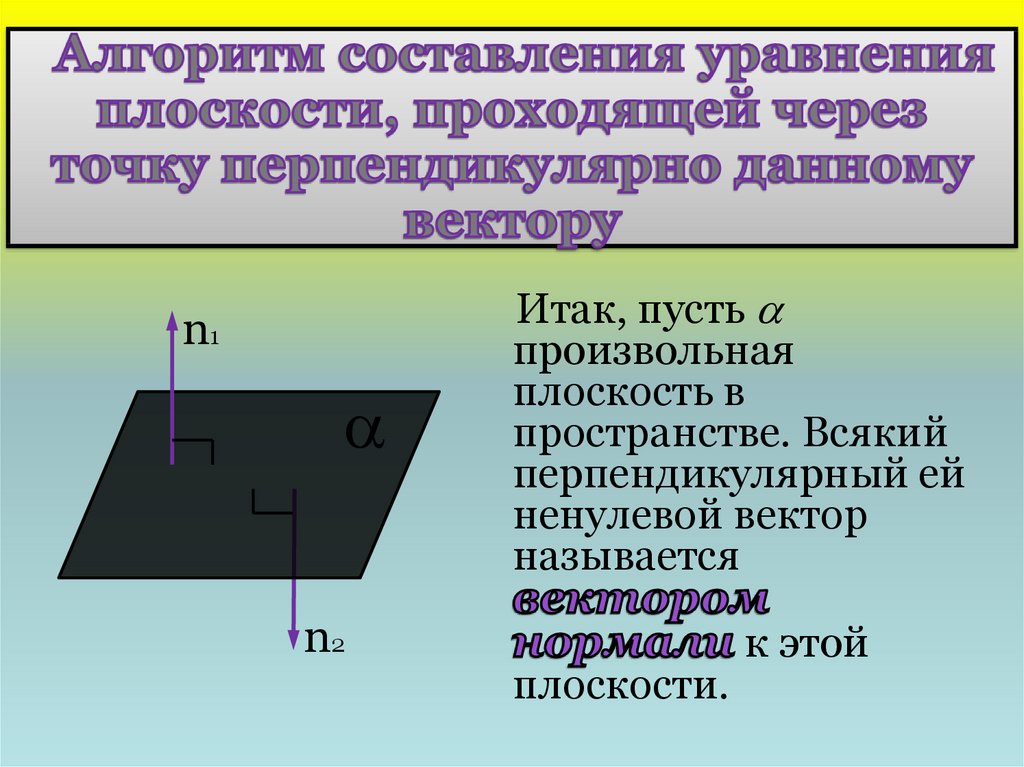
19. Алгоритм составления уравнения плоскости, проходящей через точку перпендикулярно данному вектору

n1
n2
Итак, пусть
произвольная
плоскость в
пространстве. Всякий
перпендикулярный ей
ненулевой вектор
называется
плоскости.
к этой

20. Алгоритм составления уравнения плоскости, проходящей через точку перпендикулярно данному вектору

n (A;B;C)
M0
Если известна какая-нибудь точка
плоскости M0 и какой-нибудь
вектор нормали к ней, то через
заданную точку можно провести
единственную плоскость,
перпендикулярную данному
вектору. Общее уравнение
плоскости будет иметь вид:

21.

Чтобы получить уравнение плоскости,
имеющее приведённый вид, возьмём на плоскости
произвольную точку M(x;y;z). Эта точка
принадлежит плоскости только в том случае, когда
вектор перпендикулярен вектору (рис), а для
этого, необходимо и достаточно, чтобы скалярное
произведение этих векторов было равно нулю, т.е.
Вектор задан по условию. Координаты вектора
найдём по формуле :
Теперь, используя формулу скалярного
произведения векторов , выразим скалярное
произведение в координатной форме:

22. Пример 1. Составить уравнение плоскости, проходящей через точку и перпендикулярной вектору .

: Используем формулу
A(x-x0)+B(y-y0)+C(z-z0)=0

23. Уравнение прямой в пространстве

Поскольку прямую в пространстве можно рассматривать как линию
пересечения двух плоскостей, то одним из способов аналитического
задания прямой в пространстве является задание с помощью системы
из двух уравнений
задающих пару пересекающихся плоскостей.
a1 x b1 y c1 z d1 0,
a2 x b2 y c2 z d 2 0,

24. Уравнение прямой в пространстве

Прямую, проходящую через точку A0(x0,y0,z0) с
направляющим вектором (a,b,c) можно задавать
e
параметрическими уравнениями
x at x0 ,
y bt y0 ,
z ct z .
0
В случае, если прямая в пространстве задается двумя точками
A1(x1,y1,z1), A2(x2,y2,z2), то, выбирая в качестве направляющего
вектора вектор (x2-x1,y2-y1,z2-z1) и в качестве точки А0 точку А1,
получим следующие уравнения
x ( x2 x1 )t x1 ,
y ( y2 y1 )t y1 ,
z ( z z )t z .
2
1
1

25. Упражнение 1

Какими уравнениями задаются координатные прямые?
Ответ: Ось Ox
x t,
Ось Oy
y 0,
z 0;
x 0,
, Oz
y tОсь
z 0;
x 0,
y 0,
z t.

26. Упражнение 2

Напишите параметрические уравнения прямой, проходящей через
точку А(1,-2,3) с направляющим вектором, имеющим координаты (2,3,-1).
Ответ:
x 1 2t ,
y 2 3t ,
z 3 t.

27. Упражнение 3

Напишите параметрические уравнения прямой, проходящей через
точки А1(-2,1,-3), А2(5,4,6).
Ответ:
x 2 7t ,
y 1 3t ,
z 3 9t.

28. Упражнение 4

Напишите параметрические уравнения прямой, проходящей через точку
M(1,2,-3) и перпендикулярную плоскости x + y + z + 1 = 0.
Ответ:
x 1 t,
y 2 t,
z 3 t.

29. Упражнение 5

В каком случае параметрические уравнения
x a1t x1 , x a2t x2 ,
y b1t y1 , y b2t y2 ,
z c t z , прямые?
определяют перпендикулярные
1
1
z c2t z2
Ответ: Если выполняется равенство a1a2+b1b2+c1c2=0.