Похожие презентации:
Усеченная пирамида
1.
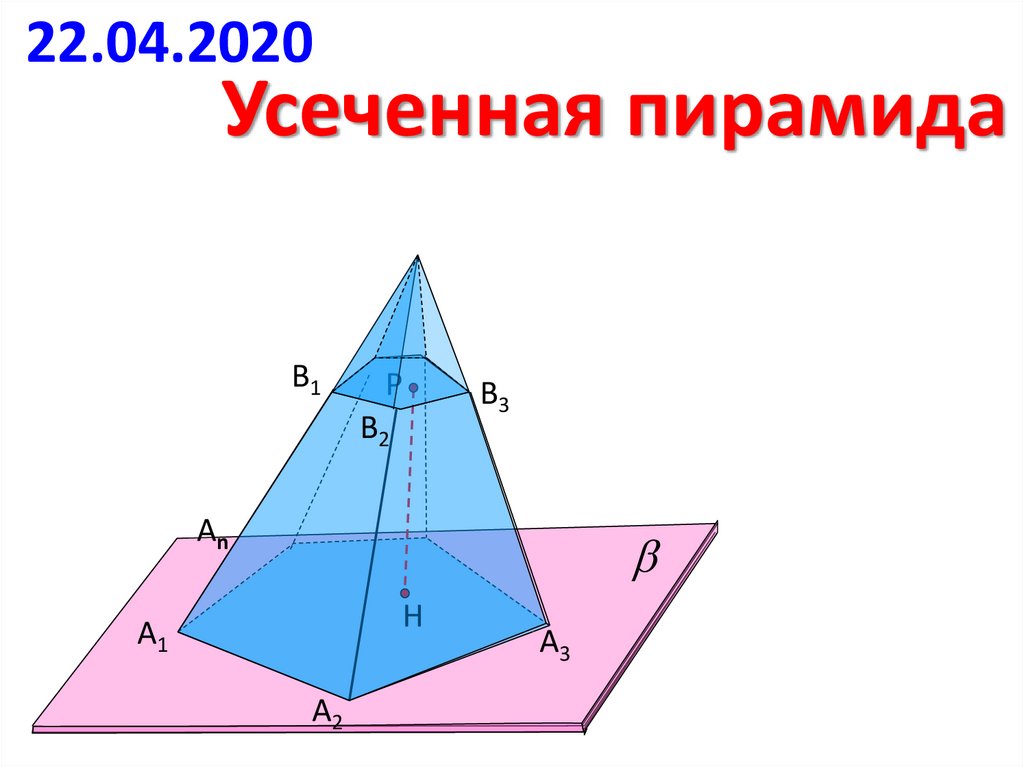
22.04.2020Усеченная пирамида
В1
Р
В2
В3
Аn
Н
А1
А2
А3
2.
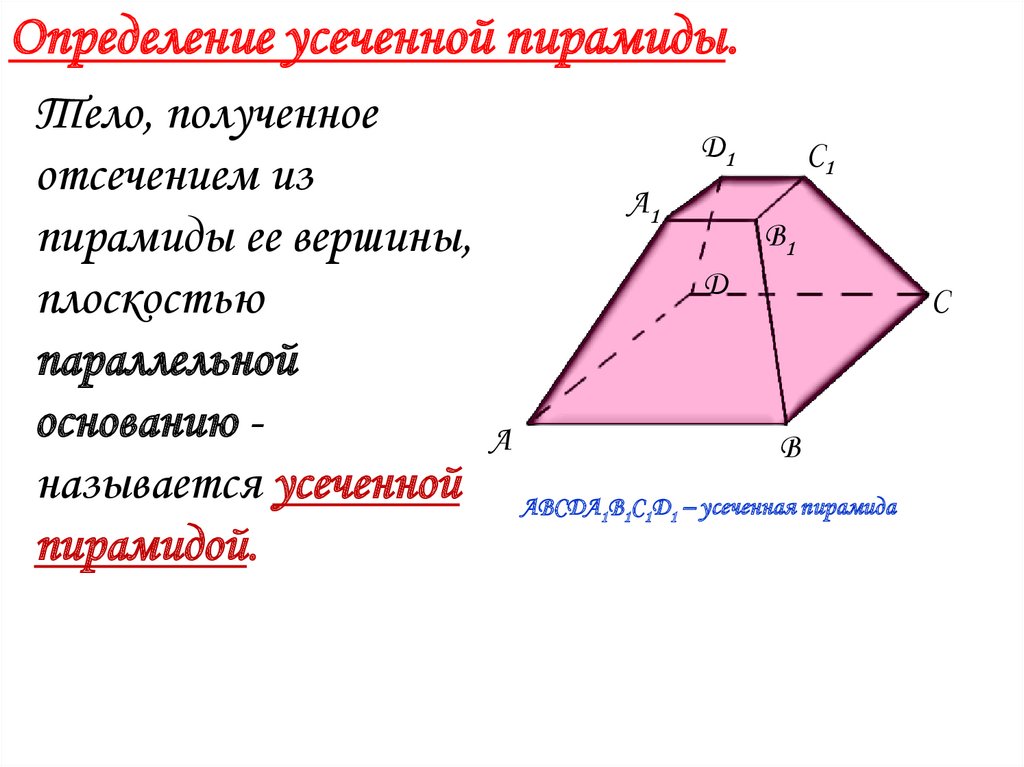
Определение усеченной пирамиды.Тело, полученное
отсечением из
пирамиды ее вершины,
плоскостью
параллельной
основанию называется усеченной
пирамидой.
D1
А1
С1
В1
D
А
С
В
АВСDА1В1С1D1 – усеченная пирамида
3.
УСЕЧЕННЫЕ ПИРАМИДЫпримеры
4.
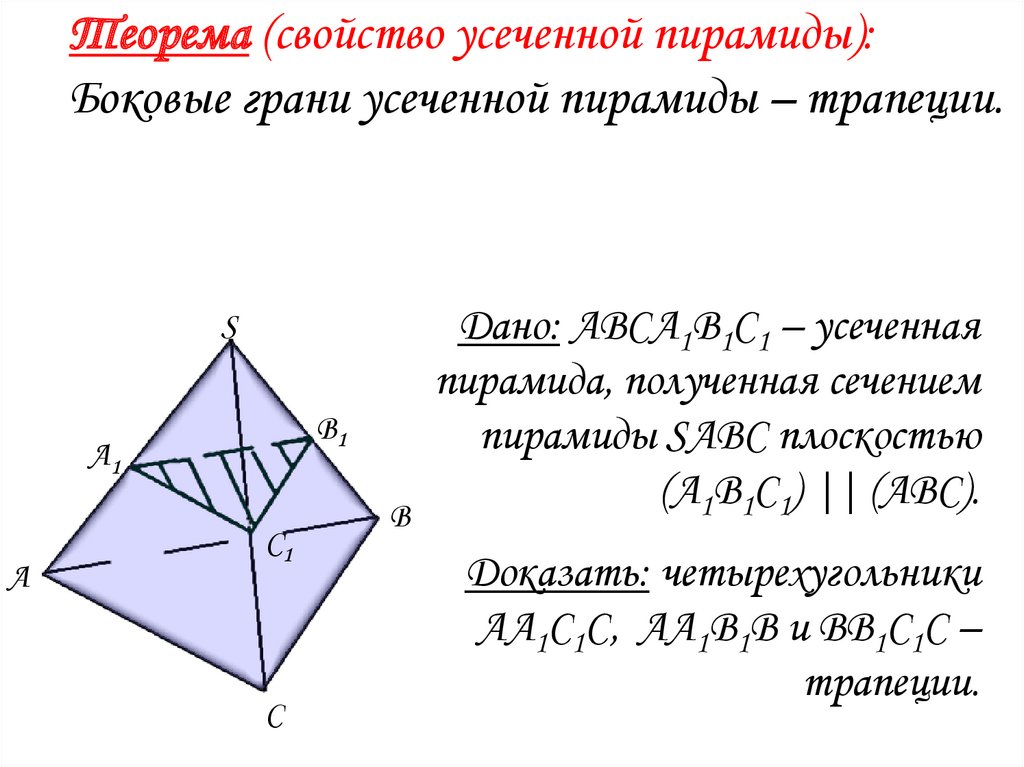
Теорема (свойство усеченной пирамиды):Боковые грани усеченной пирамиды – трапеции.
S
B1
А1
А
С1
С
B
Дано: АВСА1В1С1 – усеченная
пирамида, полученная сечением
пирамиды SАВС плоскостью
(А1В1С1) || (АВС).
Доказать: четырехугольники
АА1С1С, АА1В1В и ВВ1С1С –
трапеции.
5.
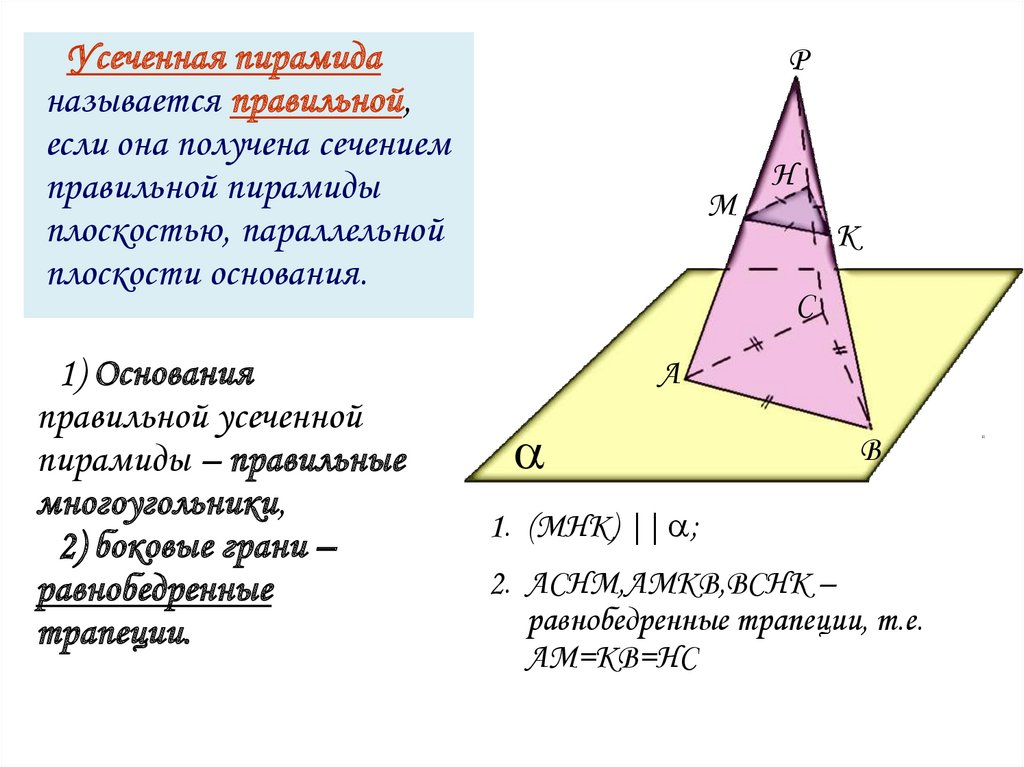
Усеченная пирамиданазывается правильной,
если она получена сечением
правильной пирамиды
плоскостью, параллельной
плоскости основания.
1) Основания
правильной усеченной
пирамиды – правильные
многоугольники,
2) боковые грани –
равнобедренные
трапеции.
Р
М
Н
К
С
А
В
1. (МНК) || ;
2. АСНМ,АМКВ,ВСНК –
равнобедренные трапеции, т.е.
АМ=КВ=НС
6.
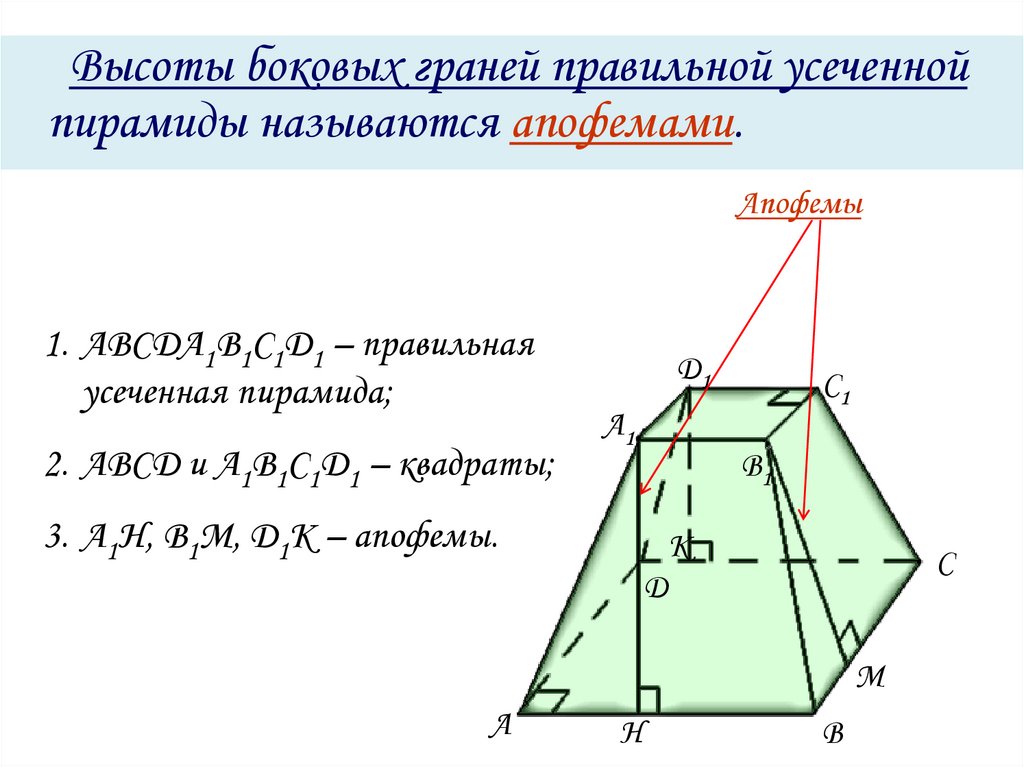
Высоты боковых граней правильной усеченнойпирамиды называются апофемами.
Апофемы
1. АВСDА1В1С1D1 – правильная
усеченная пирамида;
2. АВСD и А1В1С1D1 – квадраты;
D1
А1
С1
В1
3. А1Н, В1М, D1К – апофемы.
К
С
D
М
А
Н
В
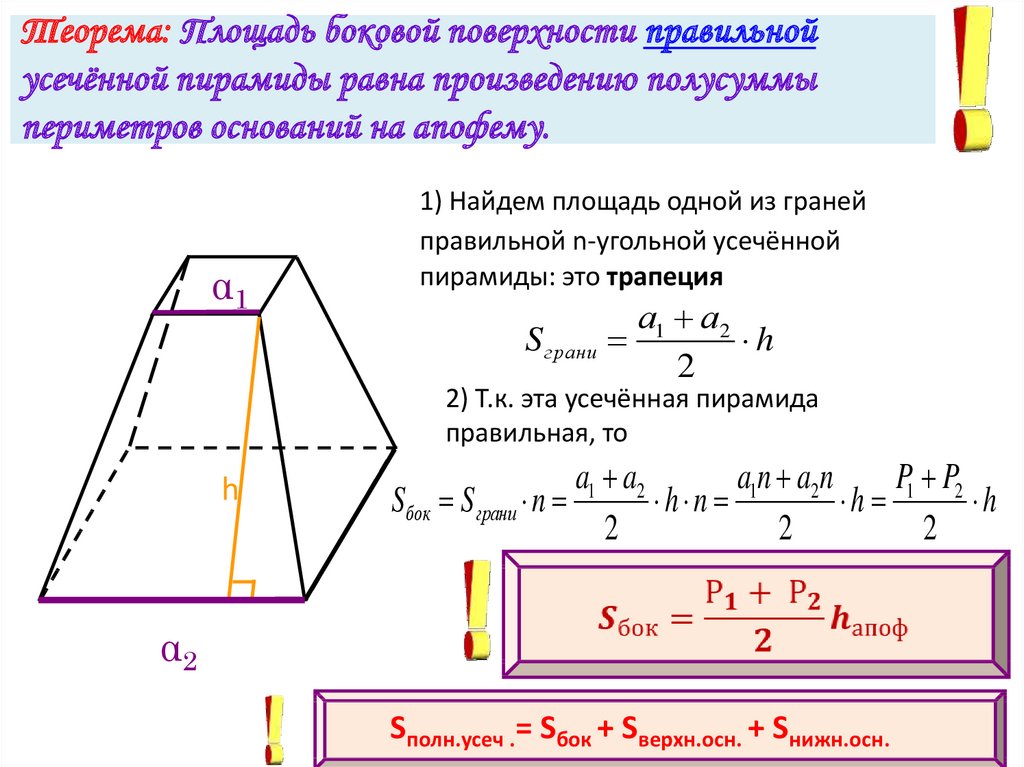
7. Теорема: Площадь боковой поверхности правильной усечённой пирамиды равна произведению полусуммы периметров оснований на
апофему.α1
1) Найдем площадь одной из граней
правильной n-угольной усечённой
пирамиды: это трапеция
а1 а2
S грани
h
2
2) Т.к. эта усечённая пирамида
правильная, то
h
a1 a2
a1n a2n
P1 P2
Sбок Sграни n
h n
h
h
2
2
2
α2
Sполн.усеч .= Sбок + Sверхн.осн. + Sнижн.осн.
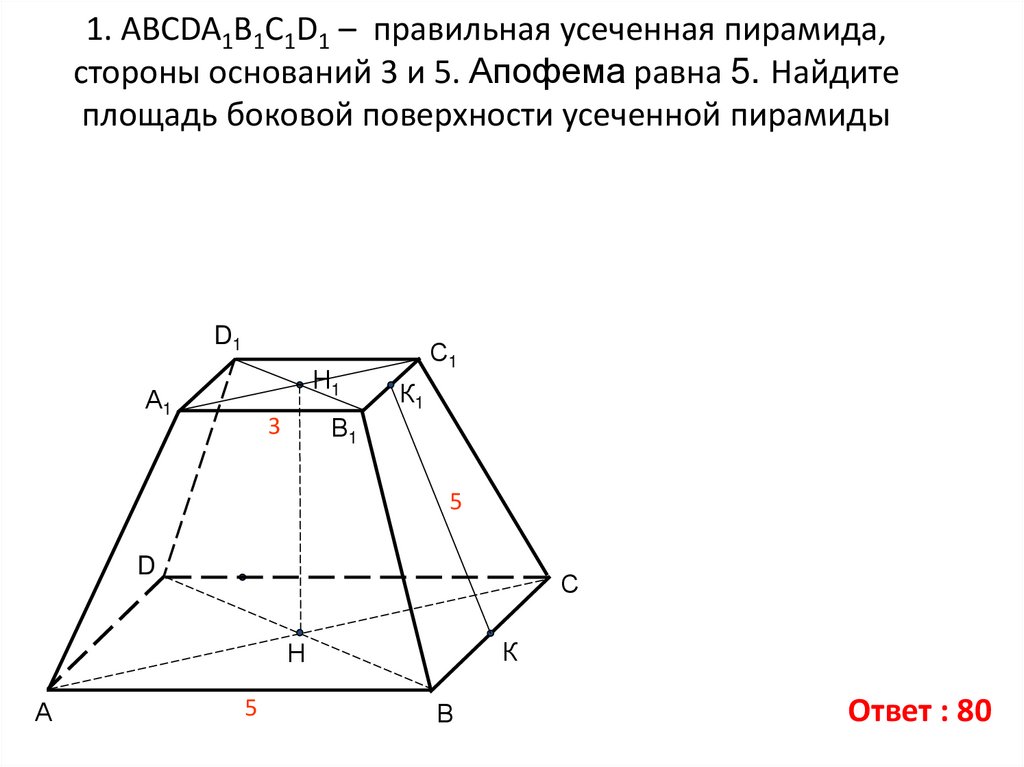
8. 1. АВСDA1B1C1D1 – правильная усеченная пирамида, стороны оснований 3 и 5. Апофема равна 5. Найдите площадь боковой поверхности
усеченной пирамидыD1
Н1
А1
С1
К1
В1
3
5
D
С
К
Н
А
5
В
Ответ : 80
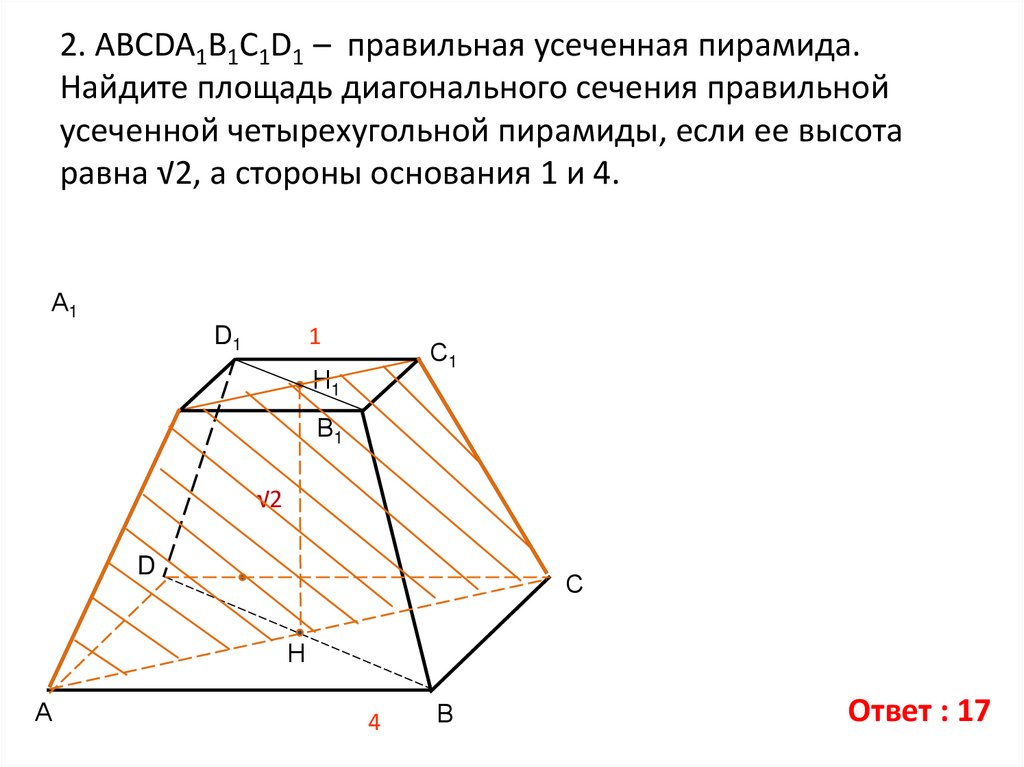
9. 2. АВСDA1B1C1D1 – правильная усеченная пирамида. Найдите площадь диагонального сечения правильной усеченной четырехугольной
пирамиды, если ее высотаравна √2, а стороны основания 1 и 4.
А1
1
D1
С1
Н1
В1
√2
D
С
Н
А
4
В
Ответ : 17
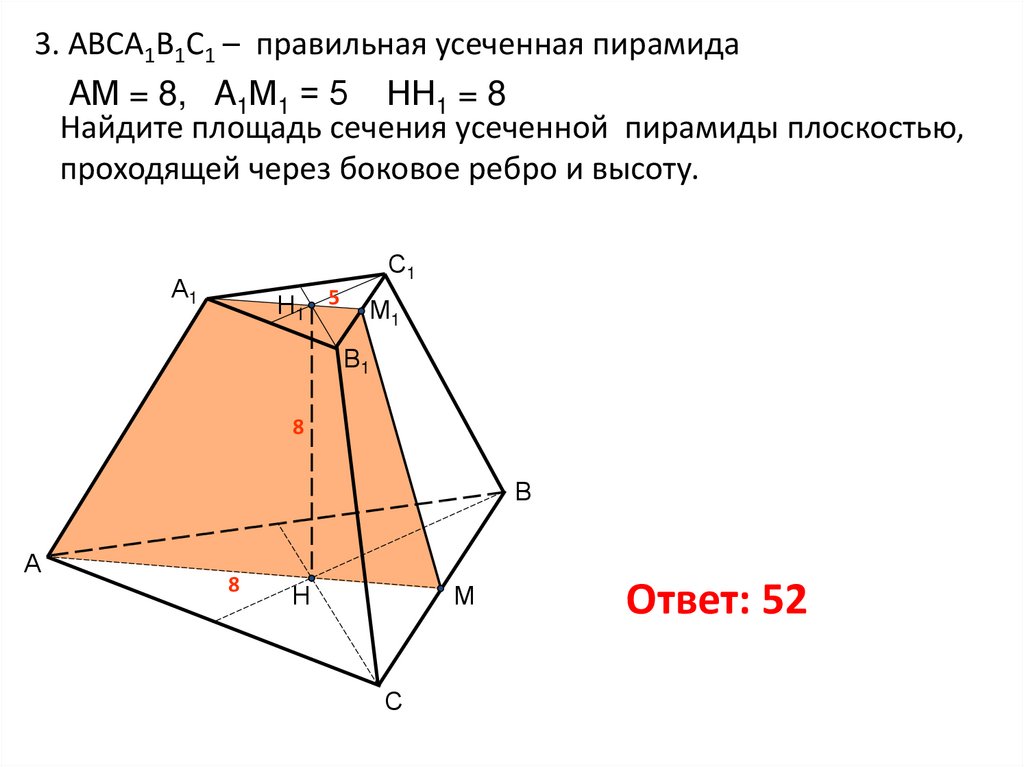
10. 3. АВСА1В1С1 – правильная усеченная пирамида
AМ = 8, A1М1 = 5 НН1 = 8Найдите площадь сечения усеченной пирамиды плоскостью,
проходящей через боковое ребро и высоту.
С1
А1
Н1 5
М1
В1
8
В
А
8
М
Н
С
Ответ: 52
11. Пирамида в задачах ЕГЭ
Домашнее задание:Пирамида в задачах ЕГЭ
1. Оформить решение задач №1-№4 в
тетрадях с чертежами и пояснениями
2. Отправить через эл. почту
12. Задача 1. АВСА1В1С1 – правильная усеченная пирамида, стороны оснований 6 и 10, апофема равна 9. Найдите площадь боковой
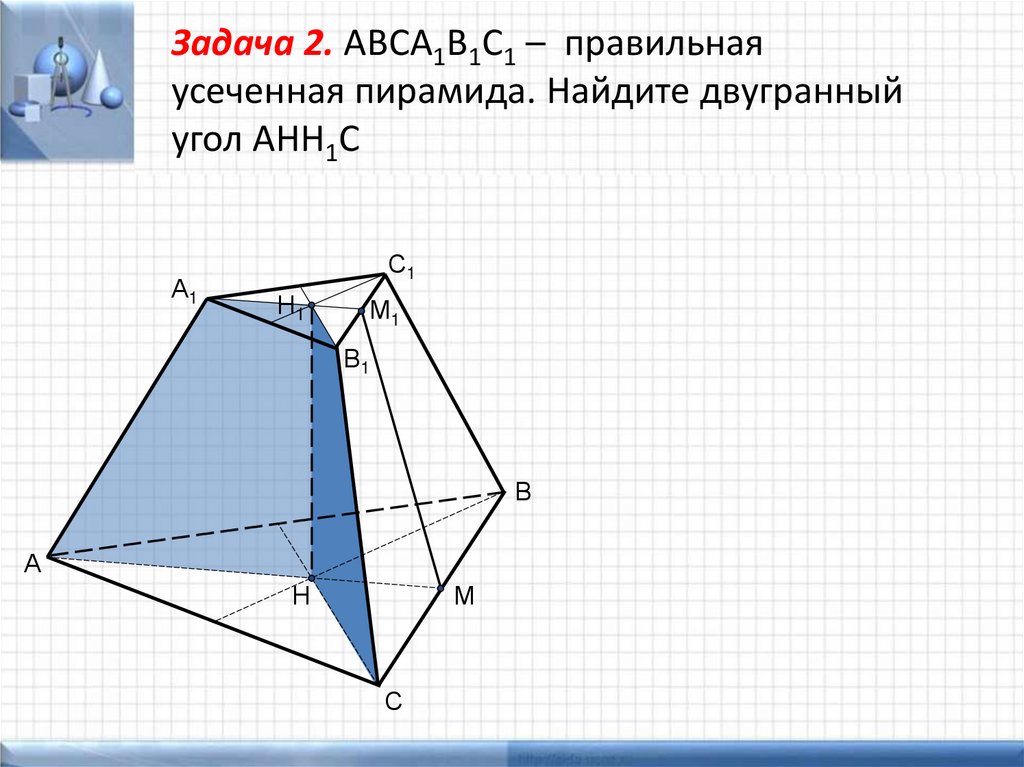
поверхности усеченной пирамиды13. Задача 2. АВСА1В1С1 – правильная усеченная пирамида. Найдите двугранный угол АНН1С
А1С1
Н1
М1
В1
В
А
М
Н
С
14.
Задача 3. В правильнойпирамиде SABCD, все ребра
которой равны 1, найдите угол
между прямыми SA и AC.
15.
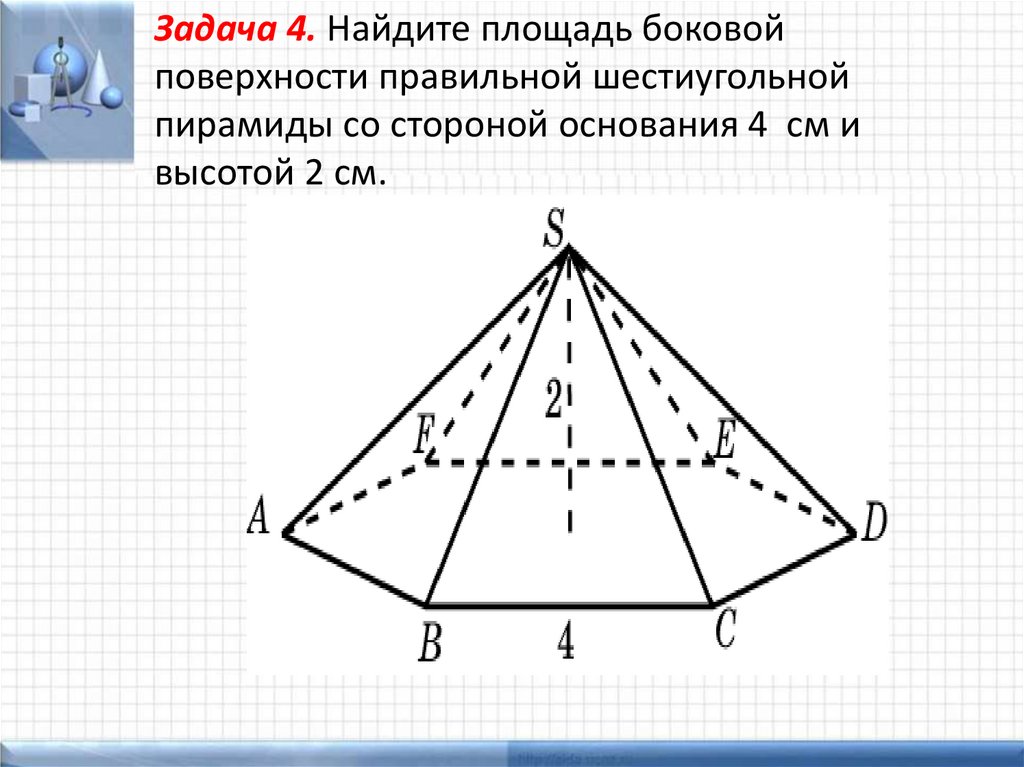
Задача 4. Найдите площадь боковойповерхности правильной шестиугольной
пирамиды со стороной основания 4 см и
высотой 2 см.





 Математика
Математика








