Усеченная пирамида

1.

2. УСЕЧЕННАЯ ПИРАМИДА

Плоскость параллельная
основанию пирамиды, разбивает
её на два многогранника. Один из
них является пирамидой, а другой
называется усечённой пирамидой.
Усеченная пирамида – это часть
полной пирамиды, заключенная
между её основанием и секущей
плоскостью, параллельной
основанию данной пирамиды

3.

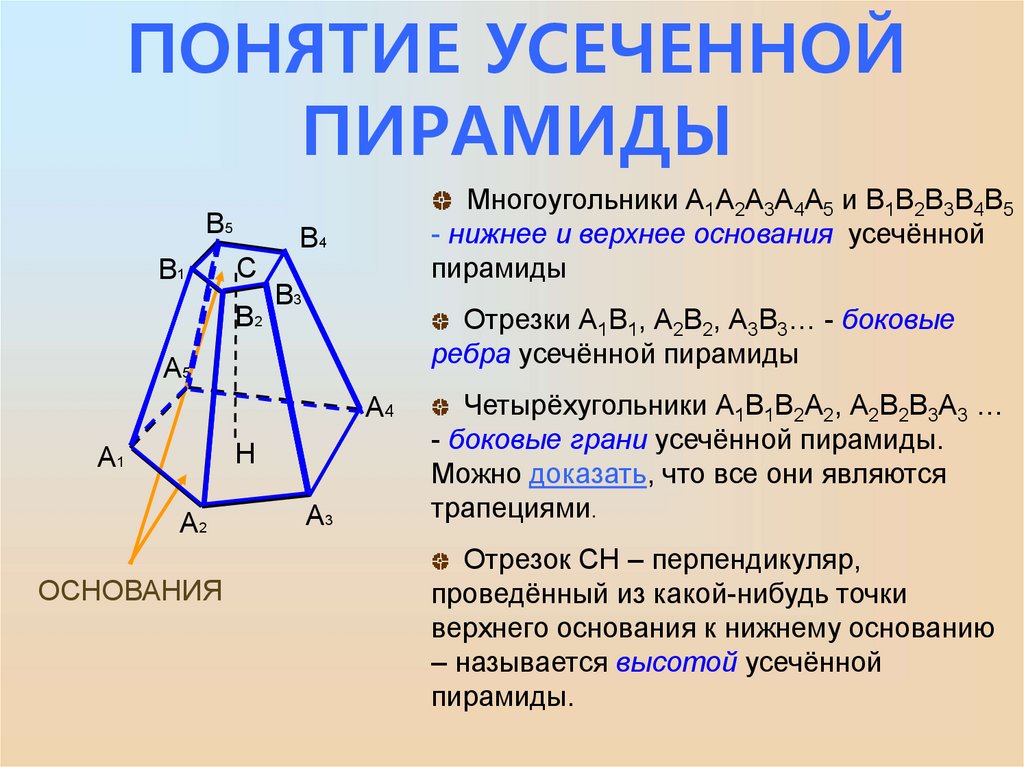
ПОНЯТИЕ УСЕЧЕННОЙ
ПИРАМИДЫ
В5
В1
С
В2
Многоугольники А1А2А3А4А5 и В1В2В3В4В5
- нижнее и верхнее основания усечённой
пирамиды
В4
В3
Отрезки А1В1, А2В2, А3В3… - боковые
ребра усечённой пирамиды
А5
А4
Н
А1
А2
ОСНОВАНИЯ
А3
Четырёхугольники А1В1В2А2, А2В2В3А3 …
- боковые грани усечённой пирамиды.
Можно доказать, что все они являются
трапециями.
Отрезок СН – перпендикуляр,
проведённый из какой-нибудь точки
верхнего основания к нижнему основанию
– называется высотой усечённой
пирамиды.

4. ПРАВИЛЬНАЯ УСЕЧЕННАЯ ПИРАМИДА

Усеченная пирамида называется
правильной, если она получена
сечением правильной пирамиды
плоскостью, параллельной
основанию.
Основания - правильные
многоугольники .
Боковые грани – равные
равнобедренные трапеции.
Высоты этих трапеций называются
апофемами.

5. ПРАВИЛЬНАЯ ПИРАМИДА

УСЕЧЕННЫЕ ПИРАМИДЫ
ПИРАМИДА
СОДЕРЖАНИЕ

6.

ПЛОЩАДЬ ПОВЕРХНОСТИ
УСЕЧЁННОЙ ПИРАМИДЫ
Площадью полной поверхности пирамиды (Sполн) пирамиды
называется сумма площадей всех её граней: основания и всех боковых
граней.
Sполн =Sбок+Sосн
Sполн.усеч .= Sбок + Sверхн.осн. + Sнижн.осн.
Площадью боковой поверхности (Sбок) пирамиды называется сумма
площадей её боковых граней.
Площадь боковой поверхности правильной пирамиды равна половине
произведения периметра основания на апофему. (Доказательство на
следующем слайде)
Площадь боковой поверхности правильной усечённой пирамиды равна
произведению полусуммы периметров оснований на апофему.

7.

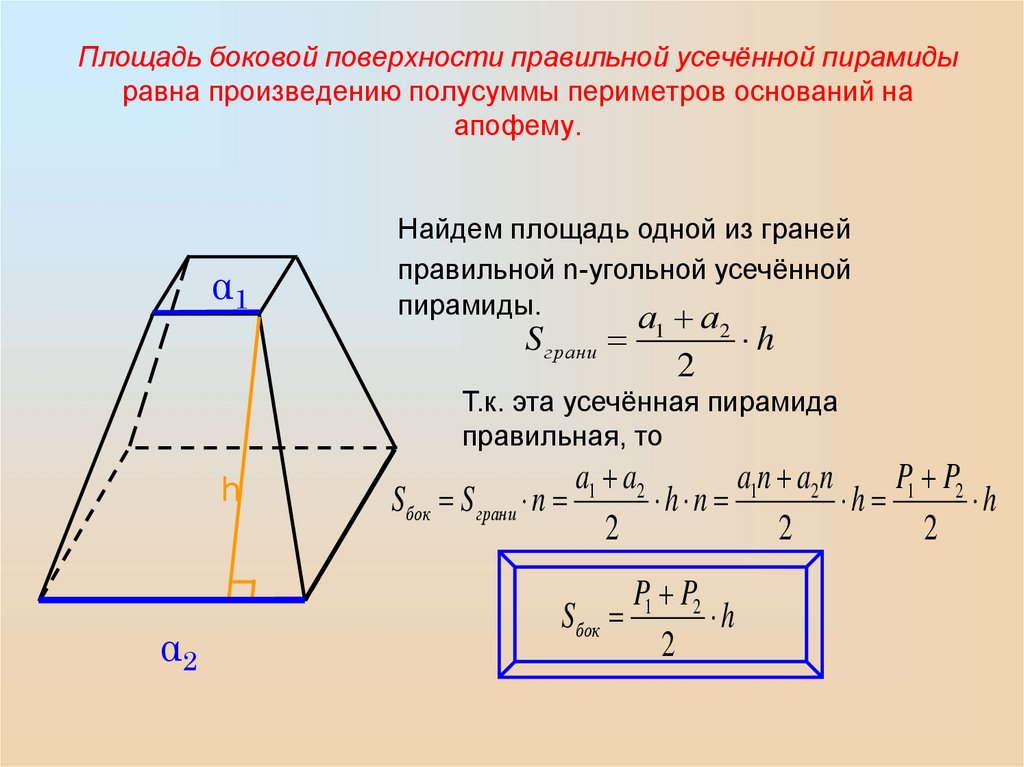
Площадь боковой поверхности правильной усечённой пирамиды
равна произведению полусуммы периметров оснований на
апофему.
α1
Найдем площадь одной из граней
правильной n-угольной усечённой
пирамиды.
а а
S грани
1
2
2
h
Т.к. эта усечённая пирамида
правильная, то
h
α2
a1 a2
a1n a2n
P1 P2
Sбок Sграни n
h n
h
h
2
2
2
P1 P2
Sбок
h
2