Похожие презентации:
Умножение вектора на число
1.
Домашнее заданиеП. 86,
№776
2.
05.05.2020Умножение вектора на число
3.
Повторяем!Отрезок, для которого указано, какая из его граничных точек считается началом, а какая
– концом, называется направленным отрезком или вектором.
Отрезок, для которого указано, какая из его граничных точек считается началом, а какая
– концом, называется направленным отрезком или вектором.
Любая точка плоскости является вектором. Такой вектор называется нулевым.
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой
или на параллельных прямых.
Коллинеарные, вектора могут быть сонаправленными, т. е. имеют одно направление.
Коллинеарные, противоположно направленные векторы имеют противоположные
направления.
Векторы называются равными, если они сонаправлены и их длины равны.
Векторы называются противоположными, если они противоположно направлены и их
длины равны.
4.
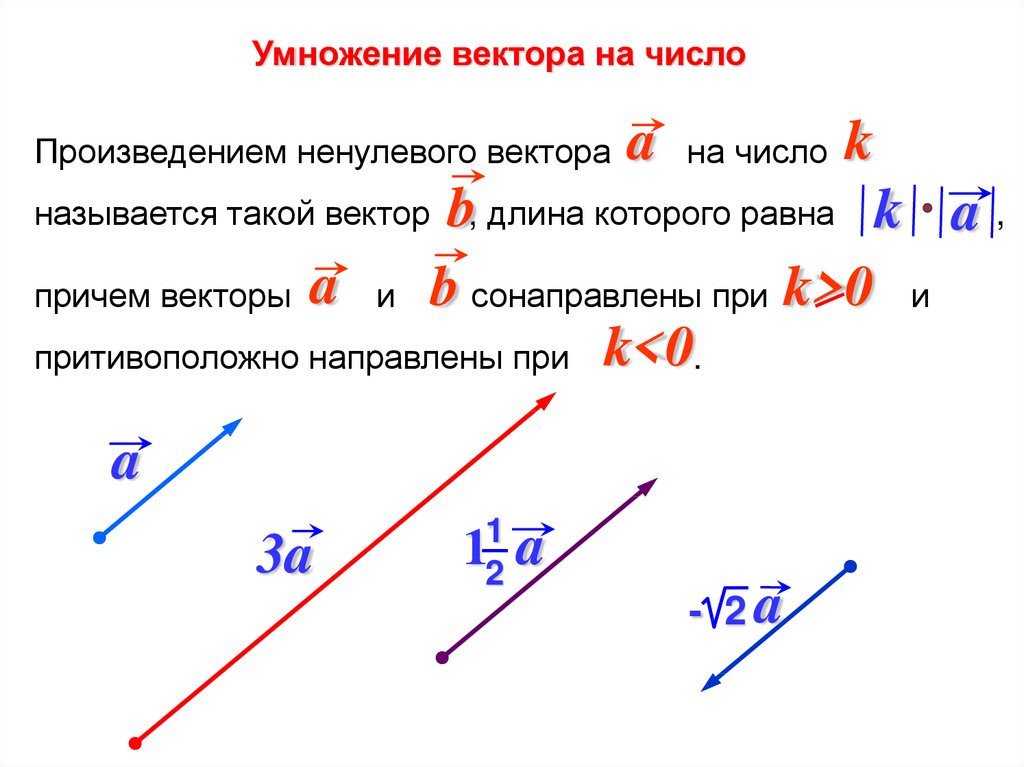
Умножение вектора на числоПроизведением ненулевого вектора
a
на число
k
b, длина которого равна k a ,
причем векторы a и b сонаправлены при k>0 и
притивоположно направлены при k<0.
называется такой вектор
a
3a
1
12
a
- 2a
5.
Умножение вектора на числоb
2b
a
2b b
2b = 2 b
1
a
2
1
a
2
1
a
2
a
=
1
2
a
6.
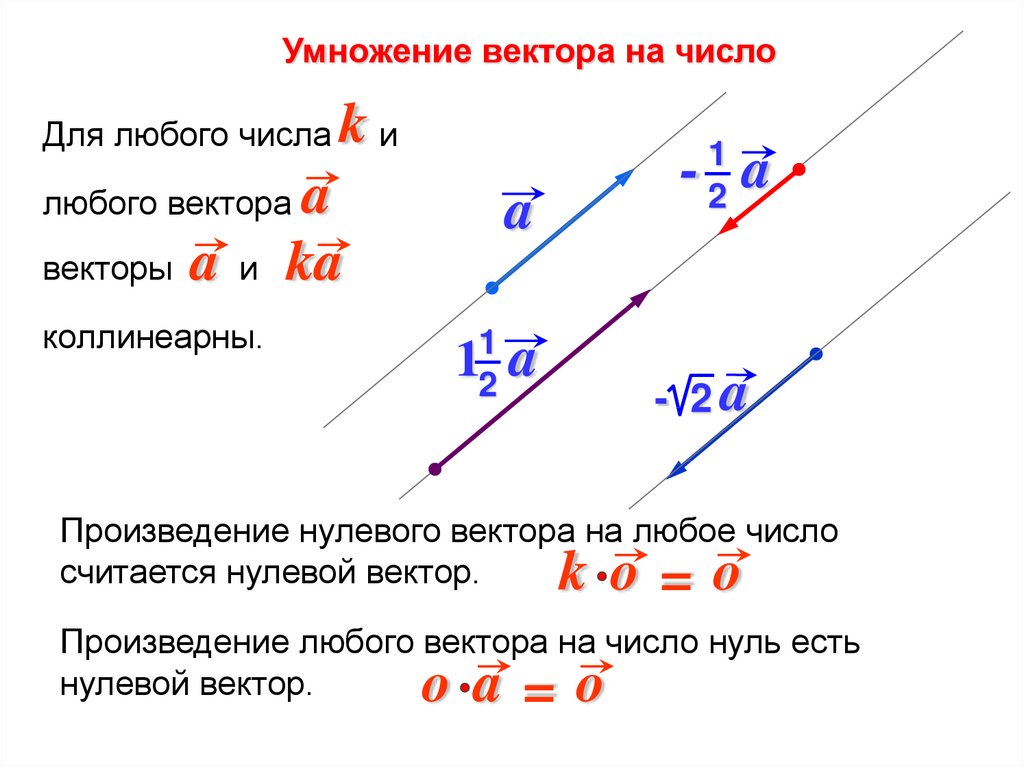
Умножение вектора на числоДля любого числа
kи
a
ka
любого вектора
векторы
a
и
коллинеарны.
1
2
- a
a
1
12
a
- 2a
Произведение нулевого вектора на любое число
считается нулевой вектор.
k o=o
Произведение любого вектора на число нуль есть
нулевой вектор.
o a=o
7.
Умножение вектора на число обладает следующимиосновными свойствами.
Для любых
равенства:
a, b
и любых чисел
k, l
справедливы
Сочетательный закон
1
(kl)a = k (l a)
Первый распределительный закон
2
(k+l)a = ka + la
Второй распределительный закон
3
k (a + b) = ka + kb
8.
Рисунок иллюстрирует сочетательный закон.Представлен случай, когда
k = 2, l = 3.
1
Сочетательный закон
(kl)a = k (l a)
a
a
a
A
O
OВ = 2OA = 2(3
a a
B
a)
a a a a
B
O
OВ = 6
a = (2 3) a
9.
Рисунок иллюстрирует первый распределительныйзакон. Представлен случай, когда
2
(k+l)a = ka + la
Первый
распределительный закон
B
la
a
ka
k = 3, l = 2.
A
OA =
ka;
AB =
la
O
OB =
(k+l)a = ka + la
10.
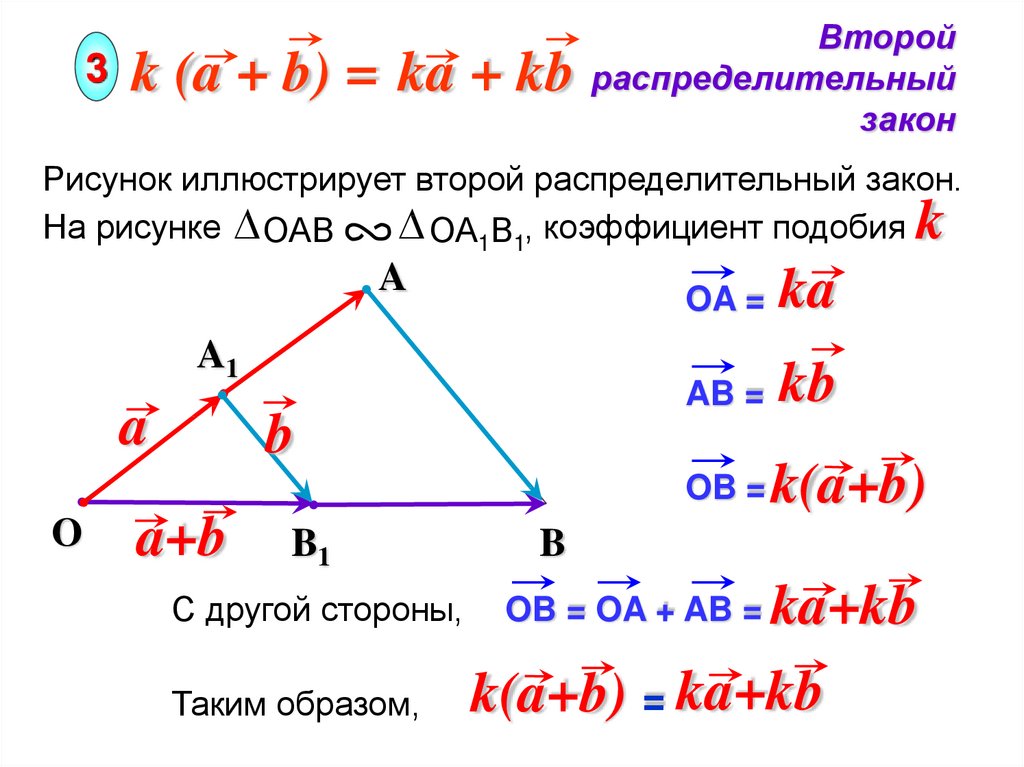
3k (a + b) = ka + kb
Второй
распределительный
закон
Рисунок иллюстрирует второй распределительный закон.
На рисунке ОАВ
ОА1В1, коэффициент подобия
k
A
OA =
ka
AB =
kb
OB =
k(a+b)
OB = OA + AB =
ka+kb
A1
a
O
b
a+b
B1
С другой стороны,
Таким образом,
B
k(a+b) = ka+kb
11.
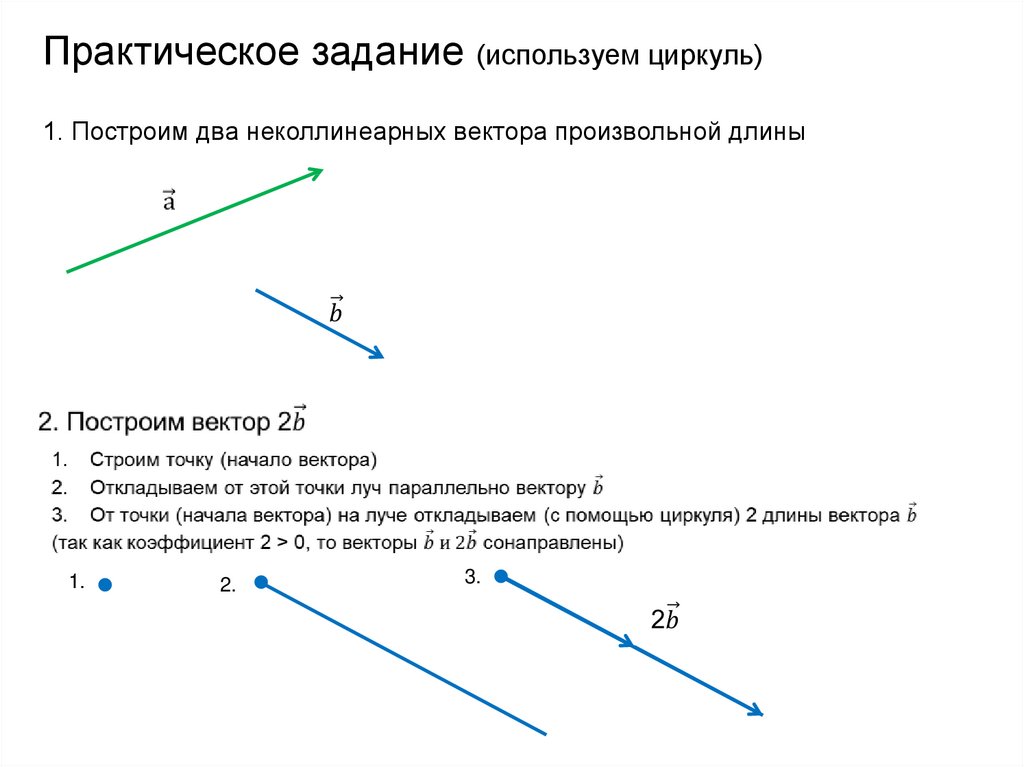
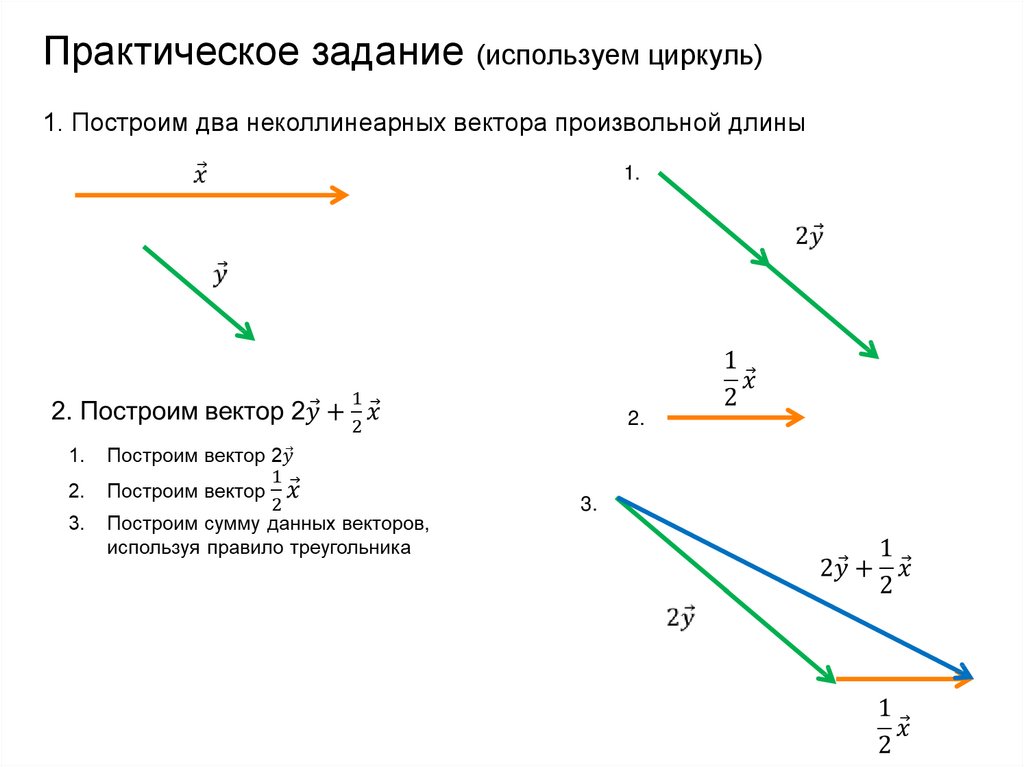
Практическое задание (используем циркуль)1. Построим два неколлинеарных вектора произвольной длины
1.
2.
3.
12.
1.2.
3.
13.
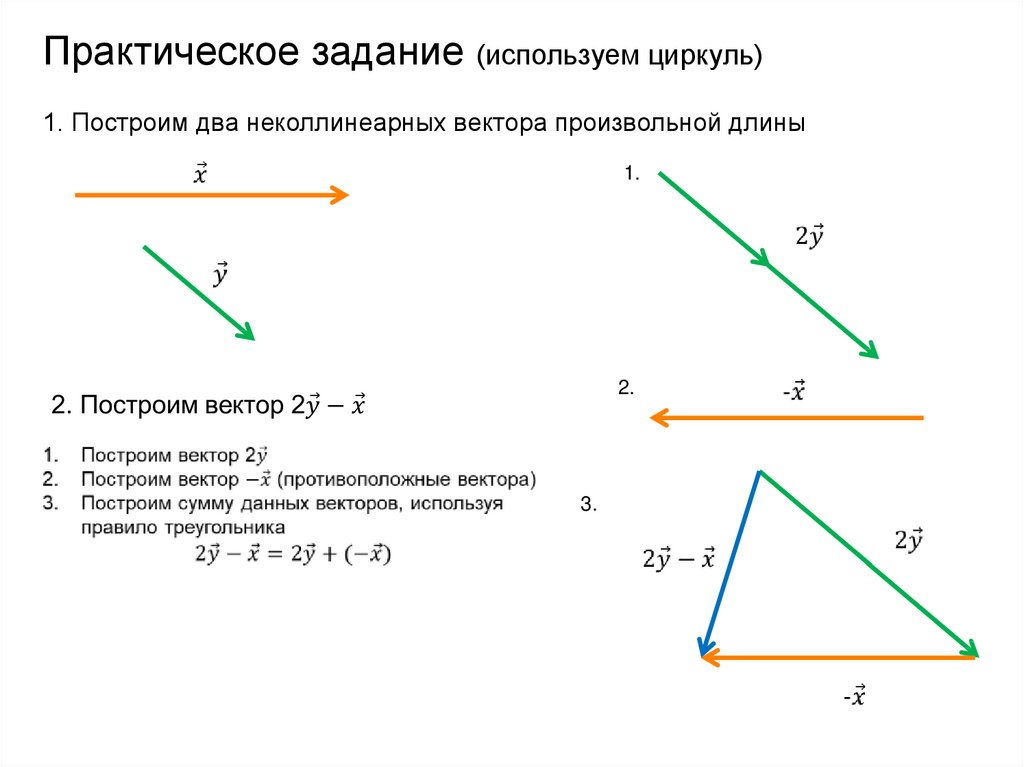
Практическое задание (используем циркуль)1. Построим два неколлинеарных вектора произвольной длины
1.
2.
3.
14.
Практическое задание (используем циркуль)1. Построим два неколлинеарных вектора произвольной длины
1.
2.
3.








 Математика
Математика








