Похожие презентации:
Простейшие тригонометрические уравнения
1. Простейшие тригонометри ческие уравнения
2. Чтобы правильно решать тригонометрические уравнения надо:
1) уметь отмечать точки на числовойокружности;
2) уметь определять значения синуса,
косинуса, тангенса и котангенса для
координат точек числовой окружности;
3) знать свойства основных
тригонометрических функций;
4) знать понятие арксинуса, арккосинуса,
арктангенса, арккотангенса и уметь
отмечать их на числовой окружности.
3. Вычисли устно:
ВЫЧИСЛИ УСТНО:4. Ответы:
5. Для каждого рисунка подберите соответствующее уравнение
ДЛЯ КАЖДОГО РИСУНКА ПОДБЕРИТЕСООТВЕТСТВУЮЩЕЕ УРАВНЕНИЕ
А)
Б)
В)
1)
2)
3)
Г)
4)
6. Для каждого рисунка подберите соответствующее уравнение
ДЛЯ КАЖДОГО РИСУНКА ПОДБЕРИТЕСООТВЕТСТВУЮЩЕЕ УРАВНЕНИЕ
А)
Б)
В)
2)
1)
4)
Г)
3)
7. Установите соответствие:
1) sin x = 0а)
2) cos x = -1
б)
3) sin x = 1
в)
4) tg x = 1
г)
5) ctgx = 0
д)
2
2 k , k Z
k , k Z
k , k Z
2
2 k , k Z
4
k , k Z
8. Установите соответствие:
1) sin x = 0а)
2) cos x = -1
б)
3) sin x = 1
в)
4) tg x = 1
г)
5) ctgx = 0
д)
2
2 k , k Z
k , k Z
k , k Z
2
2 k , k Z
4
k , k Z
9. Установите соответствие:
1) sin x = 0а)
2) cos x = -1
б)
3) sin x = 1
в)
4) tg x = 1
г)
5) ctgx = 0
д)
2
2 k , k Z
k , k Z
k , k Z
2
2 k , k Z
4
k , k Z
10. Установите соответствие:
1) sin x = 0а)
2) cos x = -1
б)
3) sin x = 1
в)
4) tg x = 1
г)
5) ctgx = 0
д)
2
2 k , k Z
k , k Z
k , k Z
2
2 k , k Z
4
k , k Z
11. Установите соответствие:
1) sin x = 0а)
2) cos x = -1
б)
3) sin x = 1
в)
4) tg x = 1
г)
5) ctgx = 0
д)
2
2 k , k Z
k , k Z
k , k Z
2
2 k , k Z
4
k , k Z
12. Установите соответствие:
1) sin x = 0а)
2) cos x = -1
б)
3) sin x = 1
в)
4) tg x = 1
г)
5) ctgx = 0
д)
2
2 k , k Z
k , k Z
k , k Z
2
2 k , k Z
4
k , k Z
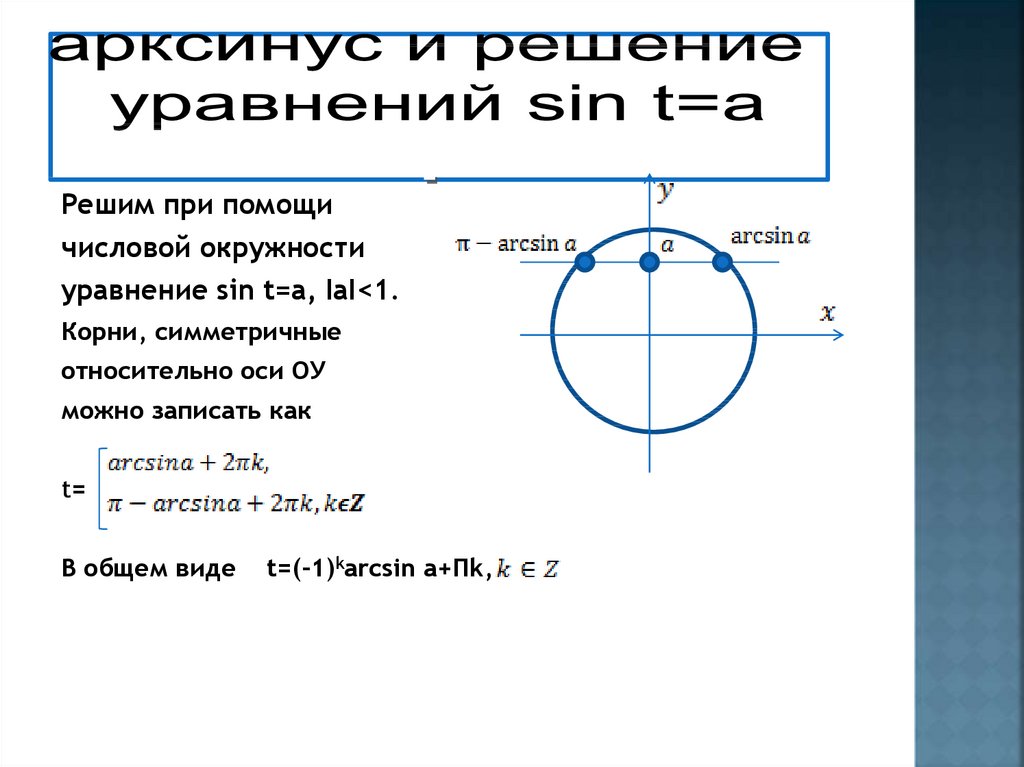
13. арксинус и решение уравнений sin t=a .
Решим при помощичисловой окружности
уравнение sin t=a, IаI<1.
Корни, симметричные
относительно оси ОУ
можно записать как
t=
В общем виде
t=(-1)karcsin a+Пk,
14. sin t = а ,|a|< 1
Частные случаи:а = -1
а=1
t = π/2+ 2 π k,
t = π/2 + 2πk,
kєZ
kє Z
а=0
t = π k,
kєZ
аrcsin (-а) = - аrcsin а
t
sint
π /6
1/2
π /4
√2 / 2
π /3
√3 / 2
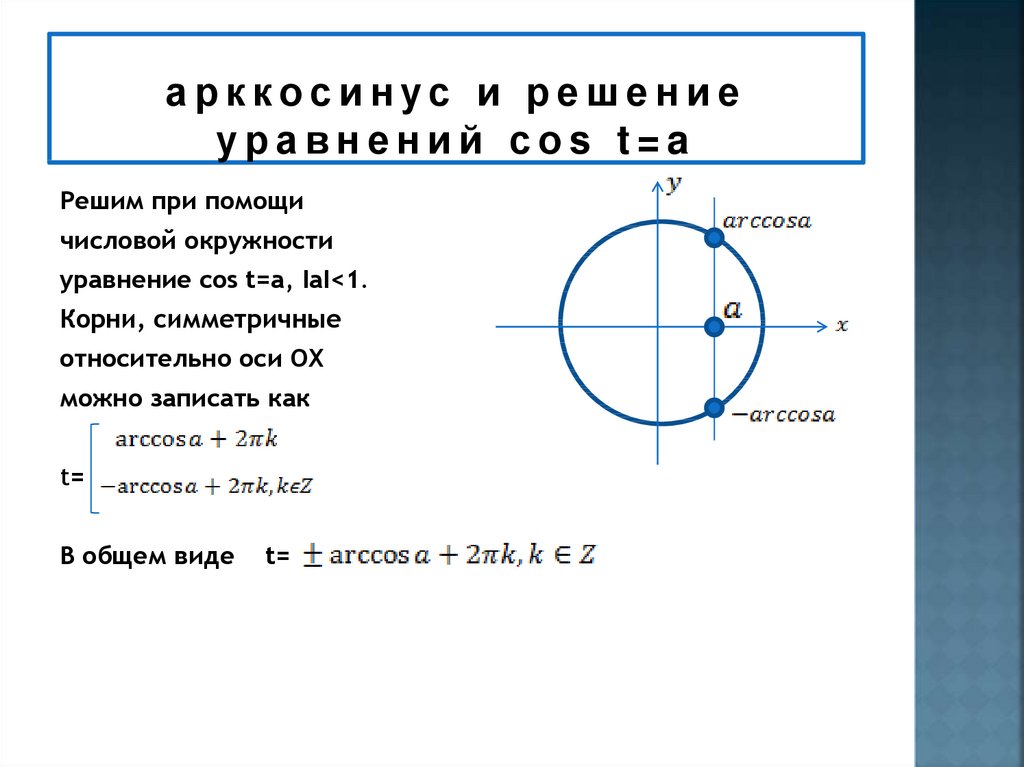
15. арккосинус и решение уравнений соs t=a
Решим при помощичисловой окружности
уравнение cos t=a, IаI<1.
Корни, симметричные
относительно оси ОX
можно записать как
t=
В общем виде
t=
16. соs t =а , |a|< 1
Частные случаи:а=0
а = -1
t= π/2 + π k,
t= π + 2 π k,
kєZ
kєZ
а=1
t= 2 π k,
kєZ
аrcсos (-а) = π - аrcсos а
t
π /6
π /4
π /3
cost
√3 / 2 √2 /2
1/2
17. арктангенс и решение уравнений tg t=a
Решим при помощичисловой окружности
уравнение tg t=a.
18. tg t = а
а=0t = πk, k є Z
Частные случаи:
а = -1
а=1
t = -π/4 + π k
t = π/4 + π k
аrctg (-а) = - аrctg а
t
tg t
π /6 π /4
√3 / 3
1
π /3
√3
19. арккотангенс и решение уравнений ctg t=a
Решим при помощичисловой окружности
уравнение ctg t=a.
20. сtg t = а,
Частные случаи:а=0
а = -1
а=1
t = π/2 + π k, t = 3π/4+ πk,
t= π/4+ πk ,
kєZ
kєZ
kєZ
аrcсtg (-а) = π - аrcсtg а
t
π /6
π /4
π /3
ctgt
√3
1
√3 / 3
21. Запомни
а=0а=1
а=-1
t
t
2
t
k
4
k
4
k
3
t
k
4
|a|< 1
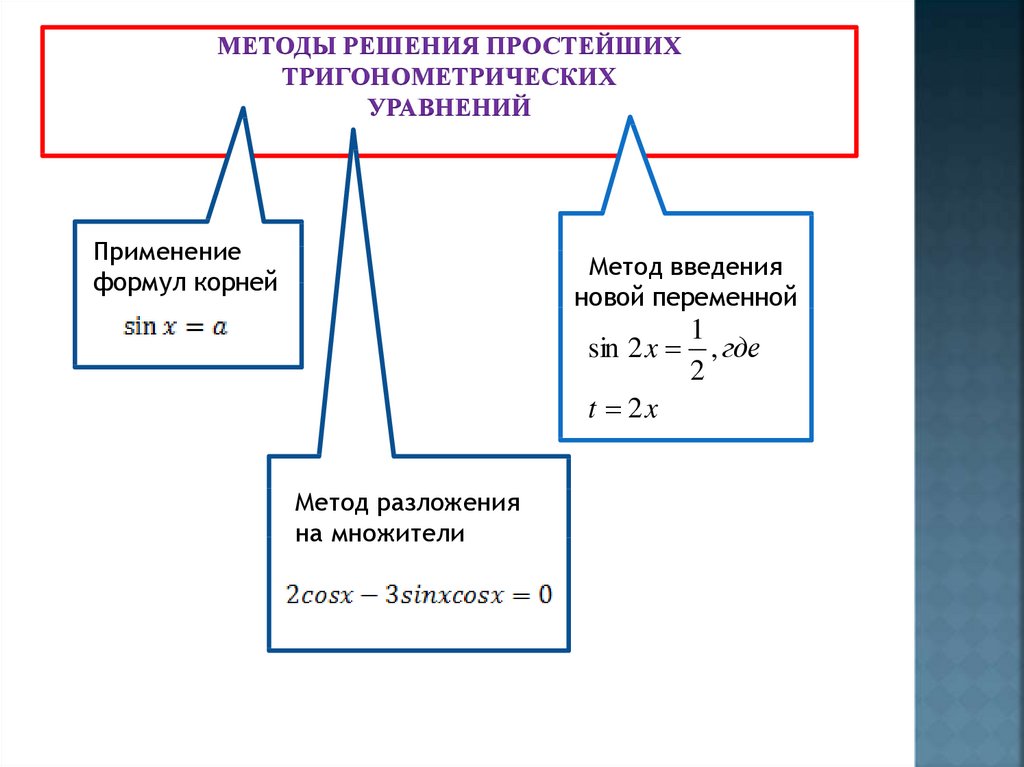
22. Методы решения простейших тригонометрических уравнений
МЕТОДЫ РЕШЕНИЯ ПРОСТЕЙШИХТРИГОНОМЕТРИЧЕСКИХ
УРАВНЕНИЙ
Применение
формул корней
Метод введения
новой переменной
ghb
sin 2 x
t 2x
Метод разложения
на множители
V
1
, где
2
23. Наша задача: свести любое тригонометрическое уравнение к простейшему виду.
24. Примеры уравнений
cos2
2
x
3
2
2
2
x arccos (
) 2 k ,
3
2
2
3
2
x
2 k ,
3
4
3
9
x
3 k , k Z
8
9
Ответ : x
3 k , k Z
8
х= ±arccos а + 2 k, k є Z
25. Примеры уравнений
1sin 2 x
2
х = (-1)n arcsin a+πn,n є z
2х = (-1)n
2х = (-1)n
х = (-1)n
Ответ: (-1)n
2
26. Примеры уравнений
cos 3x 03
3
3x
3x
2
3x
x
2
6
Это частный вид уравнения cos t=0,
t=
k ,
3
k ,
( 3)
k ,
18
k
3
Ответ : x
,k Z
18
k
3
,k Z
27. Примеры уравнений
ПРИМЕРЫ УРАВНЕНИЙx = arctg a + πk,k є z
3
tg 4 x
6 3
4x
4x
6
4x
x
6
3
6
6
k ,
k ,
k , : 4
12
k
4
,k Z
Ответ :
12
k
4
,k Z
28. Реши сам
Уровень АУровень Б
Решите уравнения:
1.
1.
2.
2.
3.
3.

























 Математика
Математика








