Шар и сфера

1.

Цель: Ввести понятия шара и сферы, площади
поверхности и объема, касательной плоскости к
сфере.
07.05.2020

2.

Лекцию записать в рабочую тетрадь полностью с рисунками.
Решить задачи.

3.

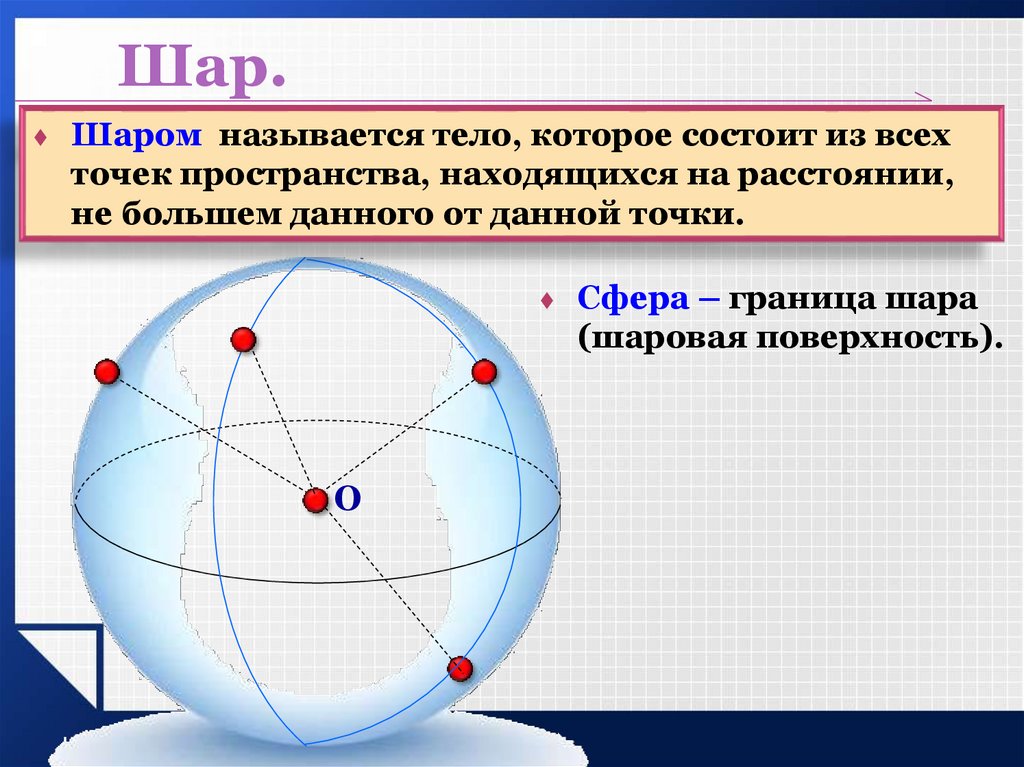
Шар.
Шаром называется тело, которое состоит из всех
точек пространства, находящихся на расстоянии,
не большем данного от данной точки.
O
Сфера – граница шара
(шаровая поверхность).

4.

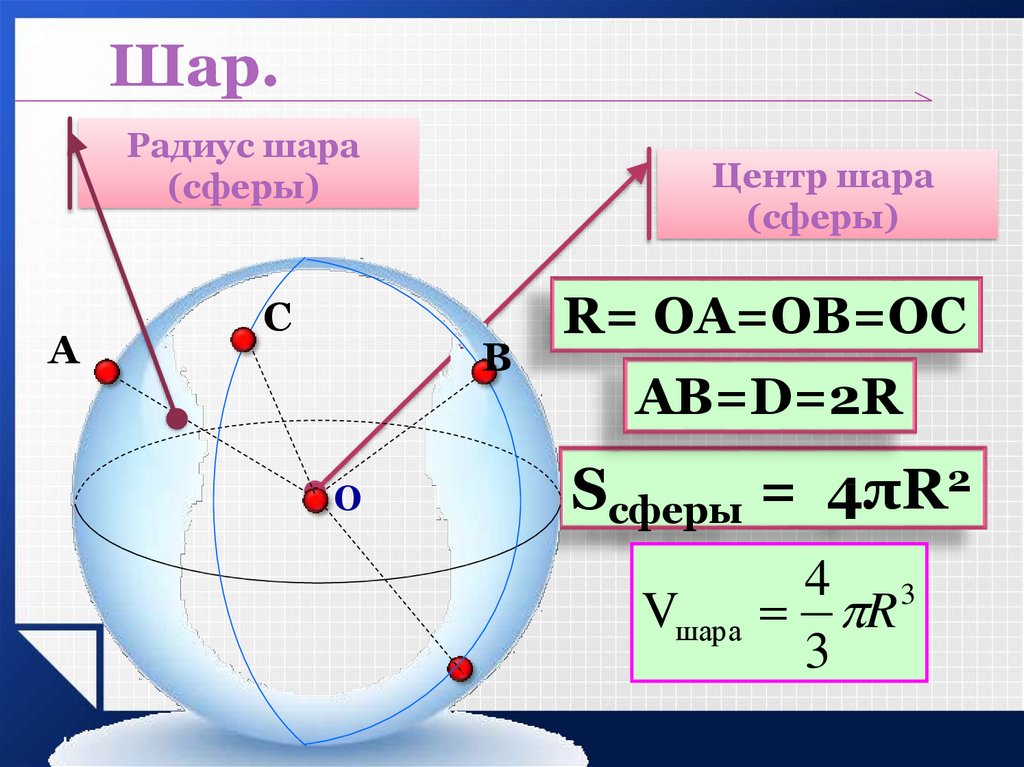
Шар.
Радиус шара
(сферы)
А
С
Центр шара
(сферы)
В
O
R= ОА=ОВ=ОС
АВ=D=2R
Sсферы = 4πR2
Vшара
4 3
R
3

5.

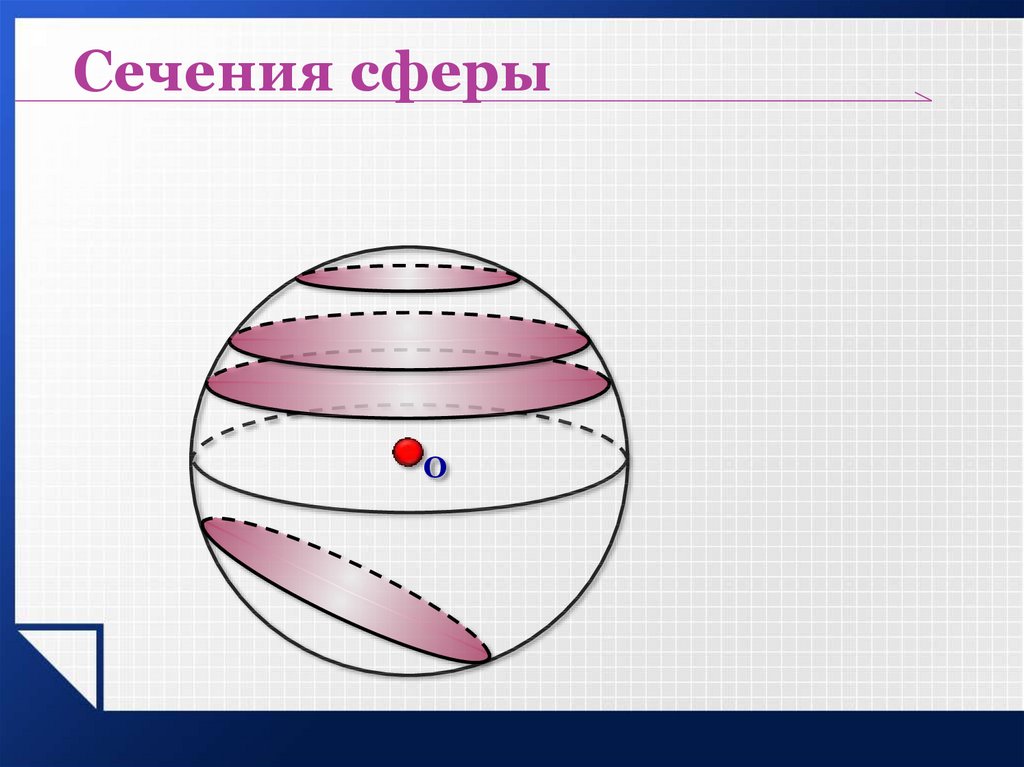
Сечения сферы
O

6.

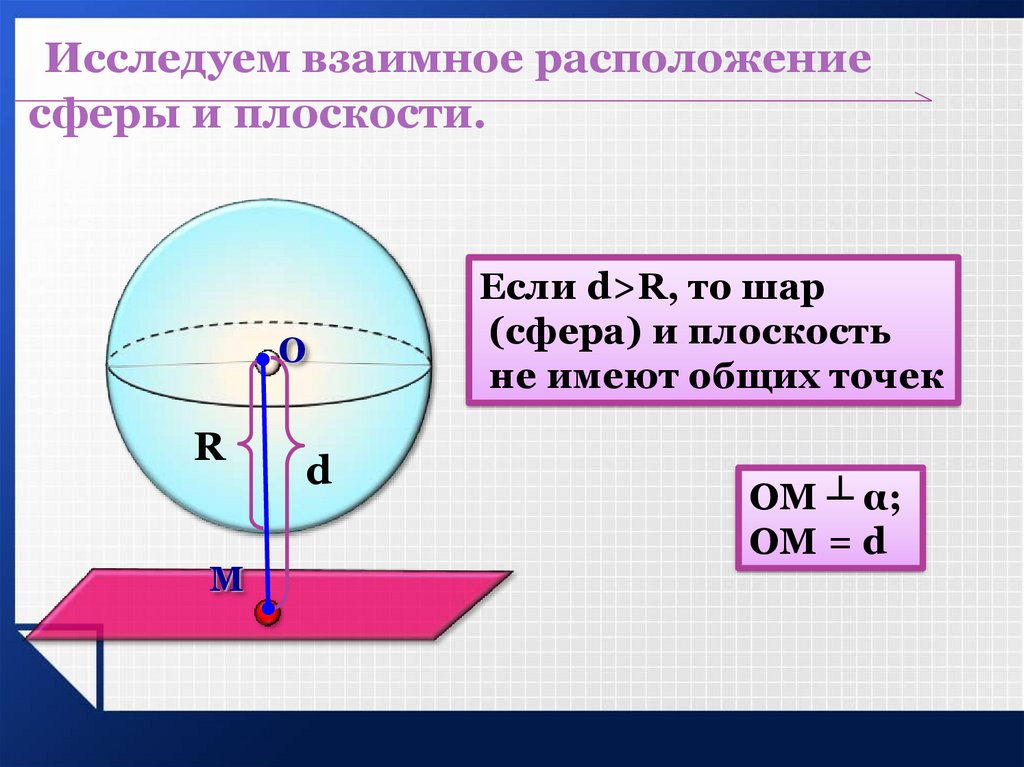
Исследуем взаимное расположение
сферы и плоскости.
О
R
М
d
Если d>R, то шар
(сфера) и плоскость
не имеют общих точек
ОМ ┴ α;
ОМ = d

7.

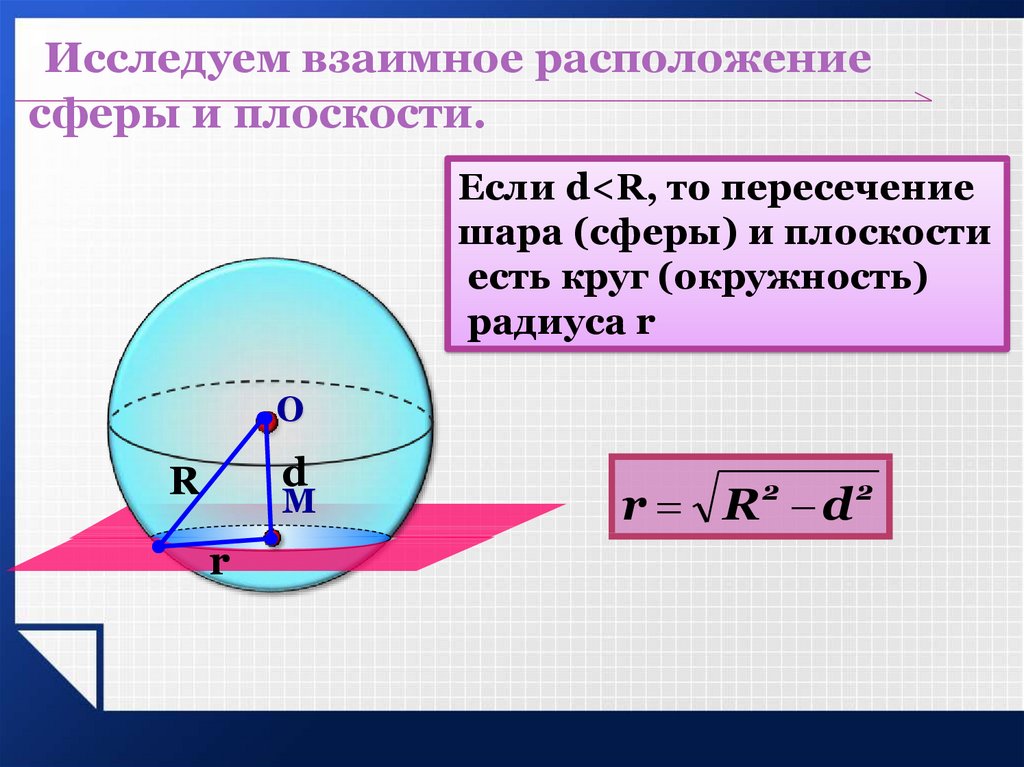
Исследуем взаимное расположение
сферы и плоскости.
Если d<R, то пересечение
шара (сферы) и плоскости
есть круг (окружность)
радиуса r
О
d
R
М
r
r R d
2
2

8.

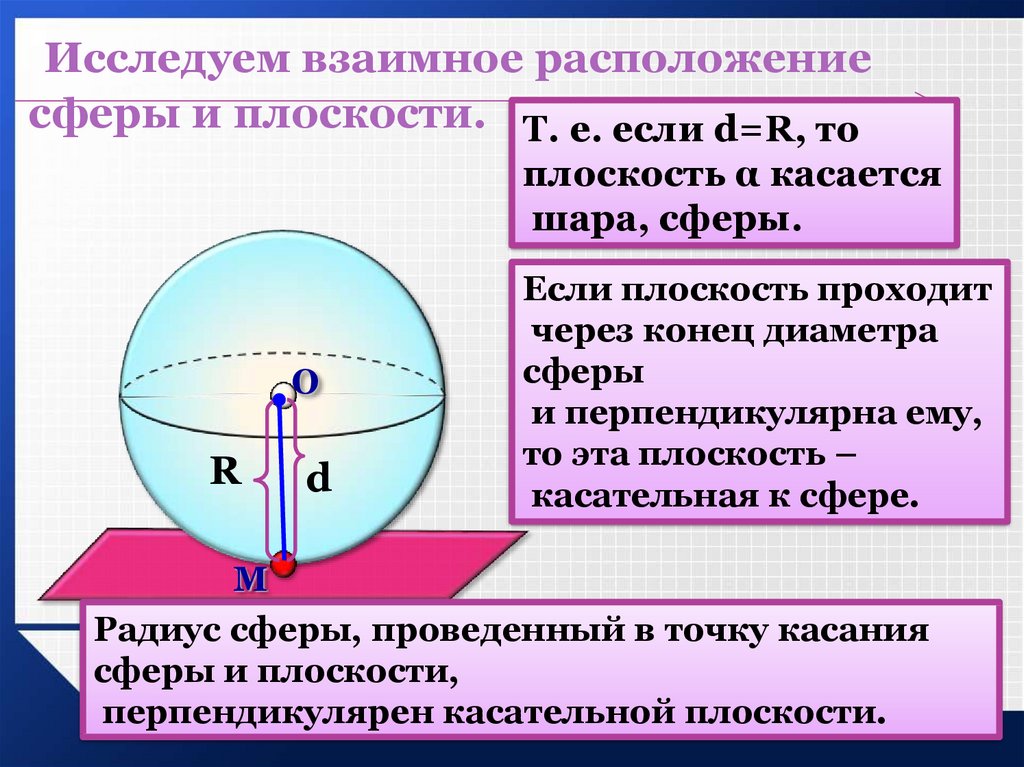
Исследуем взаимное расположение
сферы и плоскости. Т. е. если d=R, то
плоскость α касается
шара, сферы.
О
R
d
Если плоскость проходит
через конец диаметра
сферы
и перпендикулярна ему,
то эта плоскость –
касательная к сфере.
М
Радиус сферы, проведенный в точку касания
сферы и плоскости,
перпендикулярен касательной плоскости.

9. Вершины треугольника АВС лежат на сфере, радиус которой равен 13. Найдите расстояние от центра сферы до плоскости треугольника,

Задача №1
Вершины треугольника АВС лежат на сфере,
радиус которой равен 13. Найдите расстояние от
центра сферы до плоскости треугольника, если
АВ = 6, ВС = 8, АС = 10.
Схема решения.
1. 102=62 + 82, <АВС = 90º.
2. ОК ┴ α, К – центр круга,
АК =КС=5.
13 2 5 2
3. ОК =
=12.
B
C
K
O
A

10.

Решить самостоятельно
Задача № 1
Найти V шара, диаметр которого равен 8.
Задача № 2
Найти V шара, площадь поверхности которого
равна 108 π.