Дуги. Хорды. Углы

1.

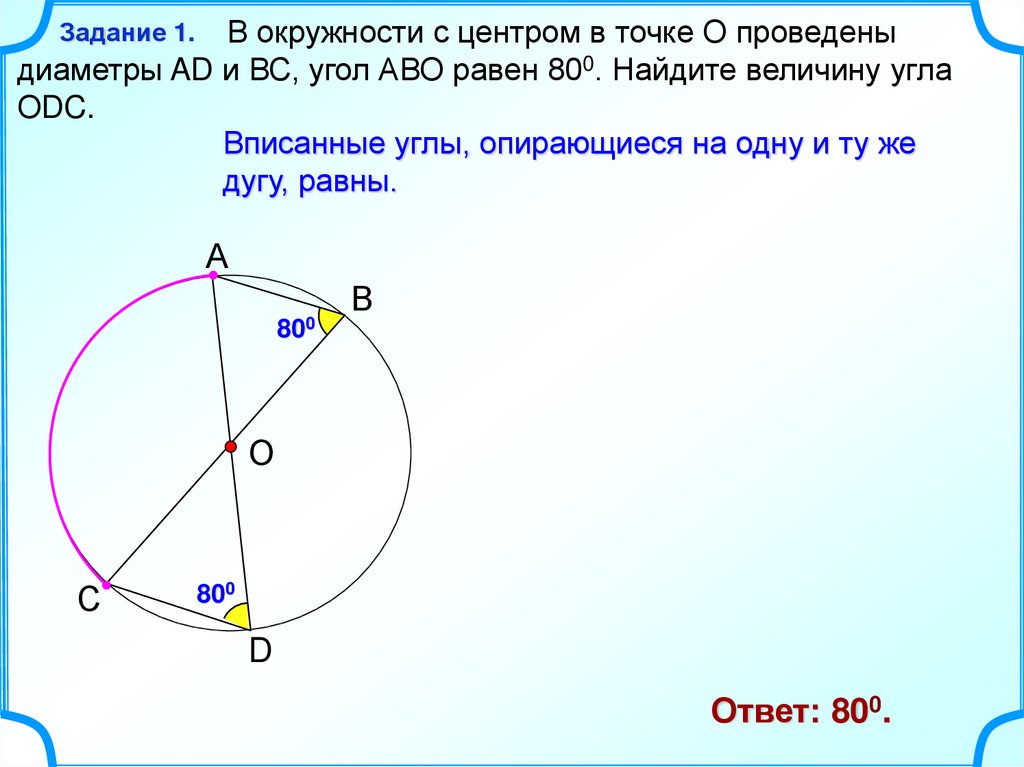
В окружности с центром в точке О проведены
диаметры AD и ВС, угол АВО равен 800. Найдите величину угла
ОDC.
Вписанные углы, опирающиеся на одну и ту же
дугу, равны.
Задание 1.
А
800
В
О
С
800
D
Ответ: 800.

2.

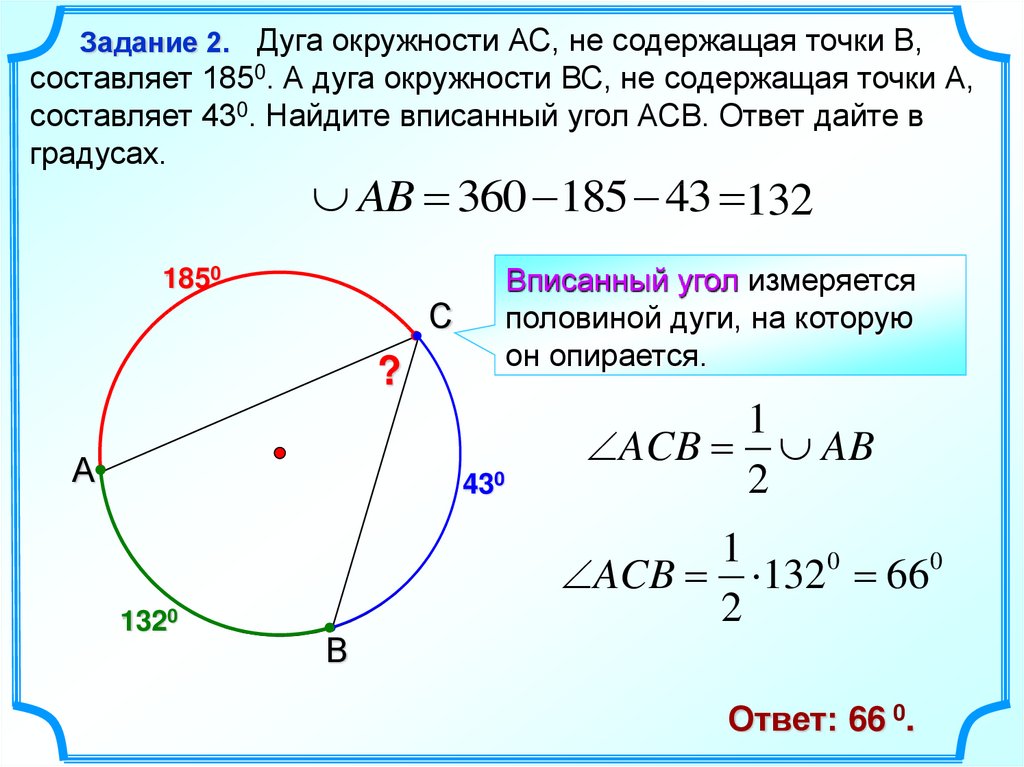
Задание 2. Дуга окружности АС, не содержащая точки В,
составляет 1850. А дуга окружности ВС, не содержащая точки А,
составляет 430. Найдите вписанный угол АСВ. Ответ дайте в
градусах.
AB 360 185 43 132
Вписанный угол измеряется
половиной дуги, на которую
он опирается.
1850
С
?
А
430
1320
1
ACB AB
2
1
0
0
ACB 132 66
2
В
Ответ: 66 0.

3.

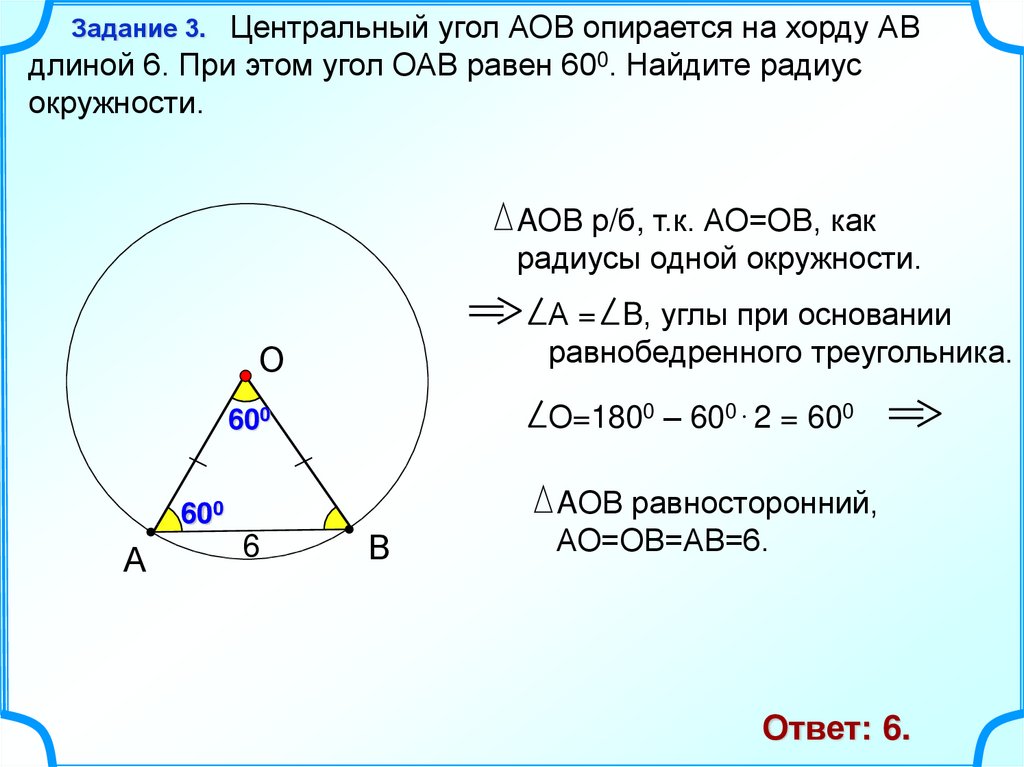
Центральный угол АОВ опирается на хорду АВ
длиной 6. При этом угол ОАВ равен 600. Найдите радиус
окружности.
Задание 3.
AОВ р/б, т.к. АО=ОВ, как
радиусы одной окружности.
А = B, углы при основании
равнобедренного треугольника.
О
О=1800 – 600 2 = 600
600
600
А
6
В
AОВ равносторонний,
АО=ОВ=АВ=6.
Ответ: 6.

4.

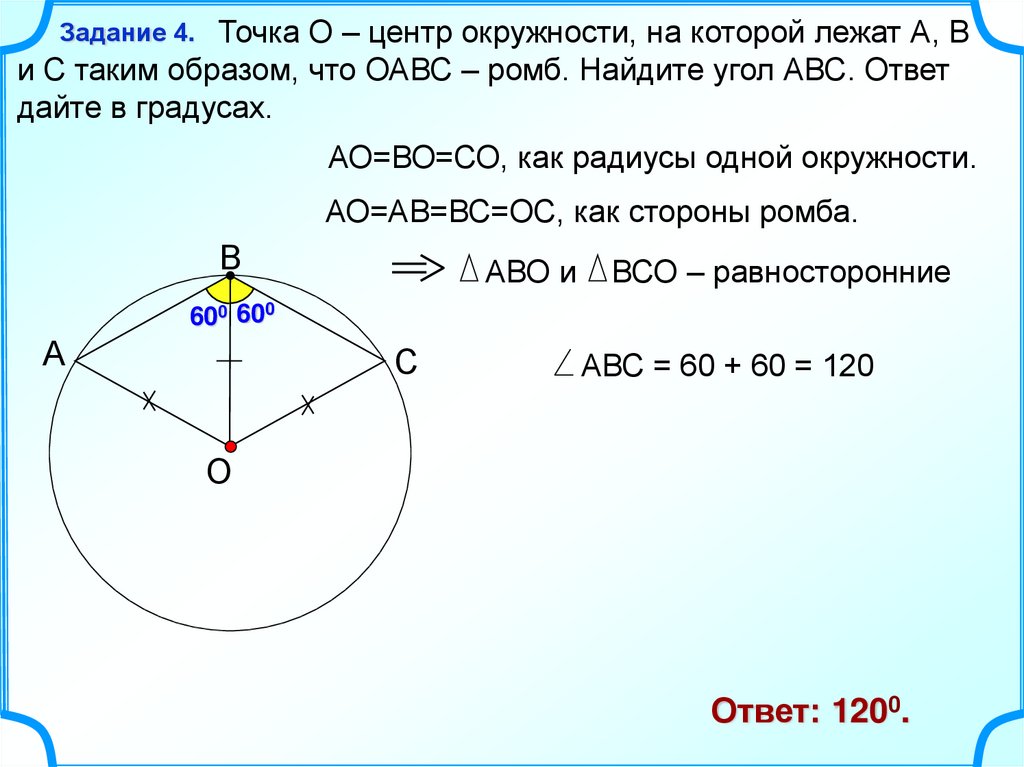
Точка О – центр окружности, на которой лежат А, В
и С таким образом, что ОАВС – ромб. Найдите угол АВС. Ответ
дайте в градусах.
Задание 4.
АО=ВО=СО, как радиусы одной окружности.
АО=АВ=ВС=ОС, как стороны ромба.
В
АВО и
ВСО – равносторонние
600 600
А
С
АВС = 60 + 60 = 120
О
Ответ: 1200.

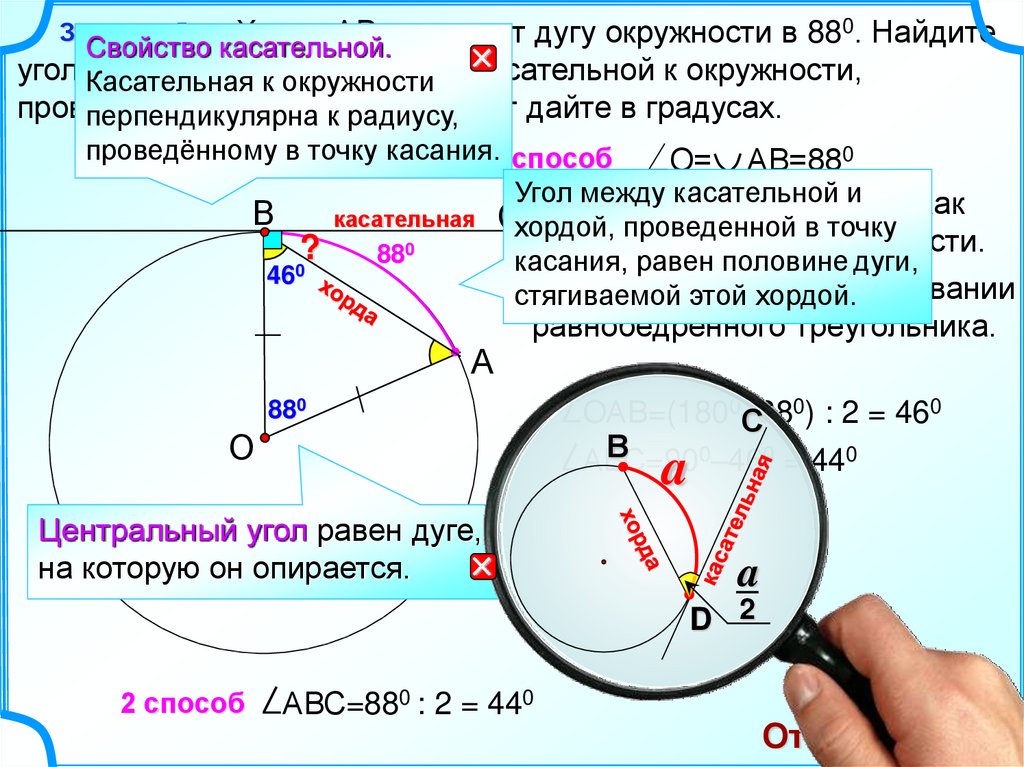
5.

0. Найдите
Хорда
АВ
стягивает
дугу
окружности
в
88
Cвойство касательной.
касательной к окружности,
угол Касательная
АВС между кэтой
хордой
и
окружности
проведённой
через точку
В. Ответ дайте в градусах.
перпендикулярна
к радиусу,
Задание 5.
проведённому в точку касания.1 способ
О= АВ=880
Угол AОВ
между– касательной
и
р/б,
т.к.
ОА=ОВ,
как
В
касательная Схордой, проведенной в точку
радиусы одной окружности.
?
880
касания,
равен половине дуги,
460
ОАВ= ОВА,
углы
при основании
стягиваемой
этой
хордой.
А
равнобедренного треугольника.
880
О
0
0
ОАВ=(1800–88
С ) : 2 = 46
В
0–460 = 440
АВС=90
a
Центральный угол равен дуге,
на которую он опирается.
a
D 2
2 способ
АВС=880 : 2 = 440
Ответ: 44 0.

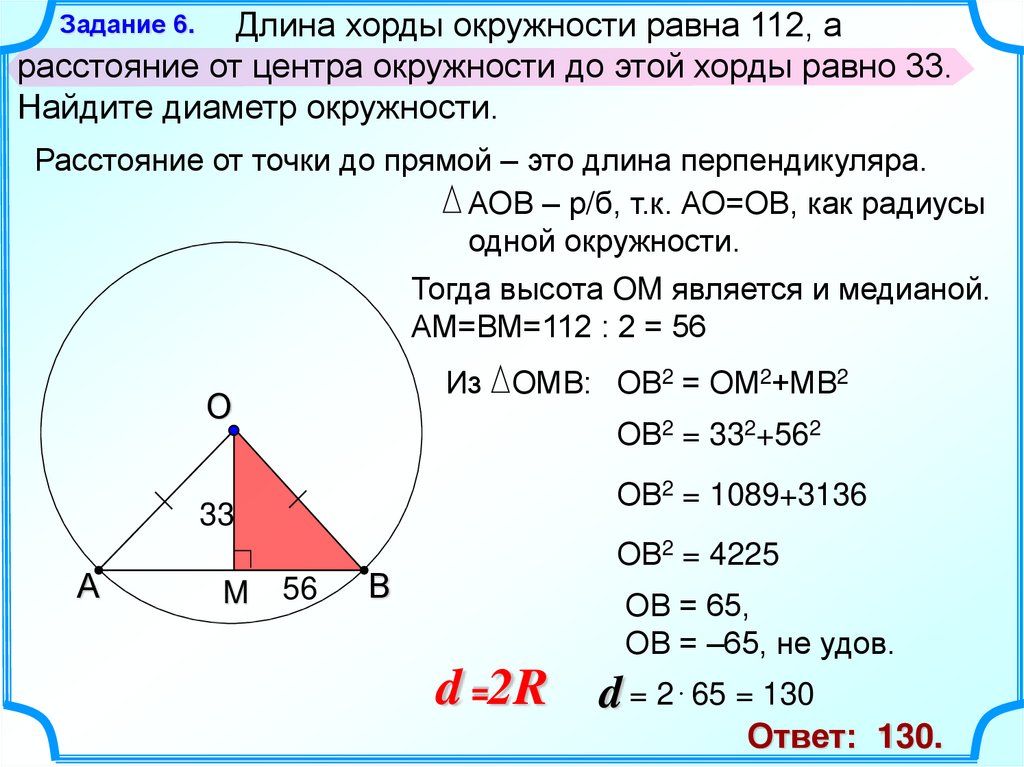
6.

Длина хорды окружности равна 112, а
расстояние от центра окружности до этой хорды равно 33.
Найдите диаметр окружности.
Задание 6.
Расстояние от точки до прямой – это длина перпендикуляра.
АОВ – р/б, т.к. АО=ОВ, как радиусы
одной окружности.
Тогда высота OM является и медианой.
АМ=ВМ=112 : 2 = 56
Из ОМВ: ОВ2 = ОМ2+МВ2
О
ОВ2 = 332+562
ОВ2 = 1089+3136
33
А
M
56
ОВ2 = 4225
В
ОВ = 65,
ОВ = –65, не удов.
d =2R
d = 2 65 = 130
Ответ: 130.

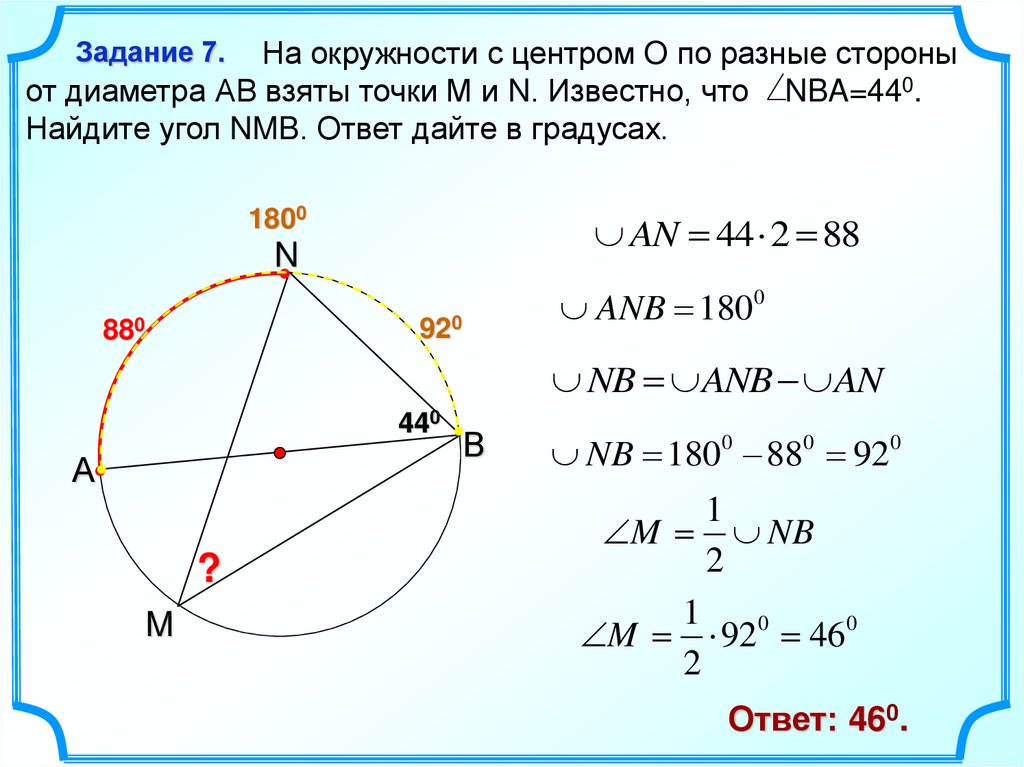
7.

На окружности с центром O по разные стороны
от диаметра АВ взяты точки М и N. Известно, что NBA=440.
Найдите угол NMB. Ответ дайте в градусах.
Задание 7.
1800
AN 44 2 88
N
ANB 1800
920
880
NB ANB AN
440
А
?
M
В
NB 1800 880 920
1
M NB
2
1
M 92 0 46 0
2
Ответ: 460.

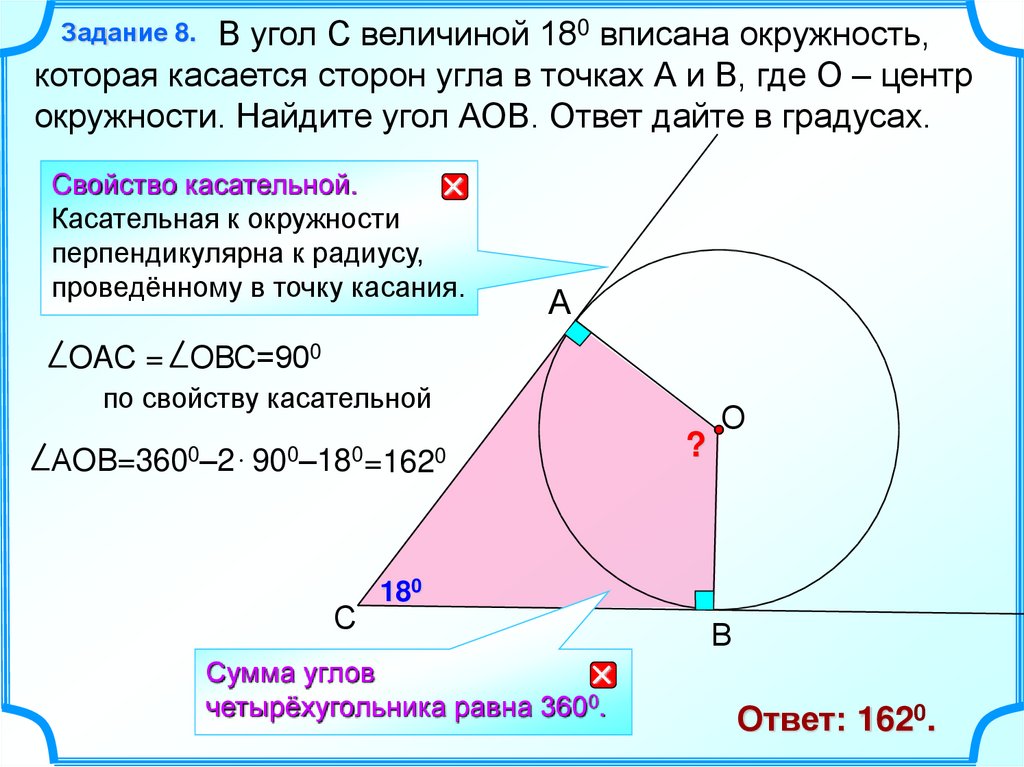
8.

В угол С величиной 180 вписана окружность,
которая касается сторон угла в точках А и В, где О – центр
окружности. Найдите угол АОВ. Ответ дайте в градусах.
Задание 8.
Cвойство касательной.
Касательная к окружности
перпендикулярна к радиусу,
проведённому в точку касания.
А
OAС = ОВС=900
по свойству касательной
АOВ=3600–2 900–180=1620
С
?
О
180
Сумма углов
четырёхугольника равна 3600.
В
Ответ: 1620.

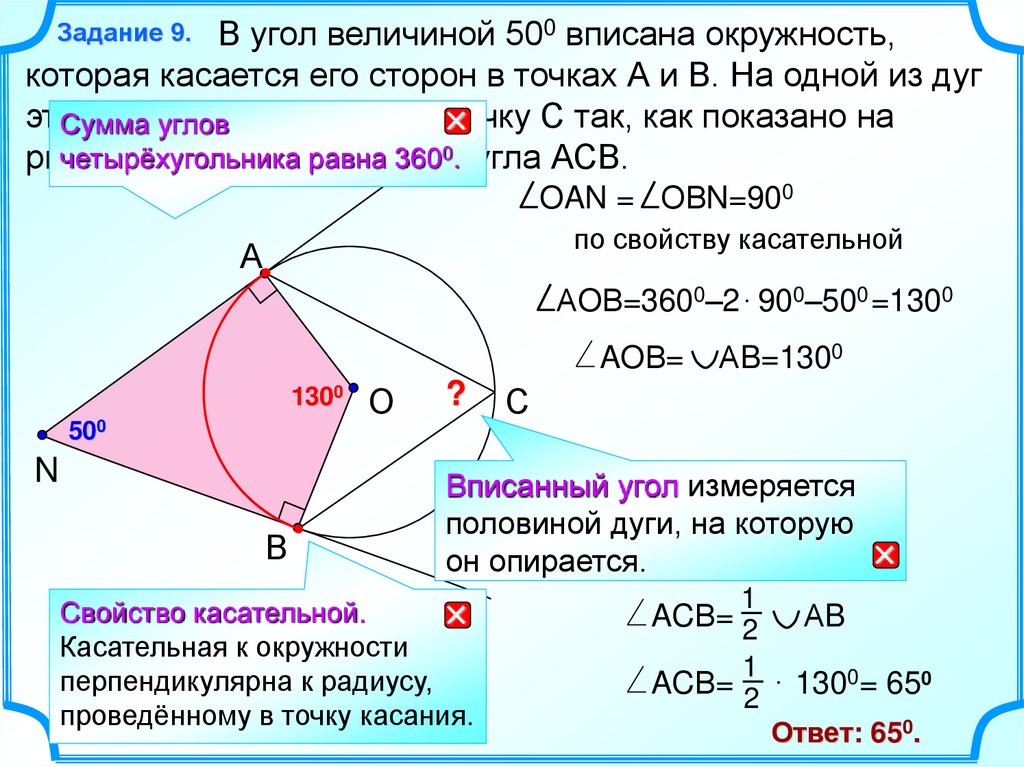
9.

В угол величиной 500 вписана окружность,
которая касается его сторон в точках А и В. На одной из дуг
этой
окружности
выбрали
точку С так, как показано на
Сумма
углов
четырёхугольника
3600. угла АСВ.
рисунке.
Найдите равна
величину
Задание 9.
OAN = ОВN=900
по свойству касательной
А
АOВ=3600–2 900–500 =1300
AOВ=
1300
500
N
В
О
?
АB=1300
С
Вписанный угол измеряется
половиной дуги, на которую
он опирается.
Cвойство касательной.
Касательная к окружности
перпендикулярна к радиусу,
проведённому в точку касания.
1
ACВ= 2 АB
1
ACВ= 2 1300= 650
Ответ: 650.

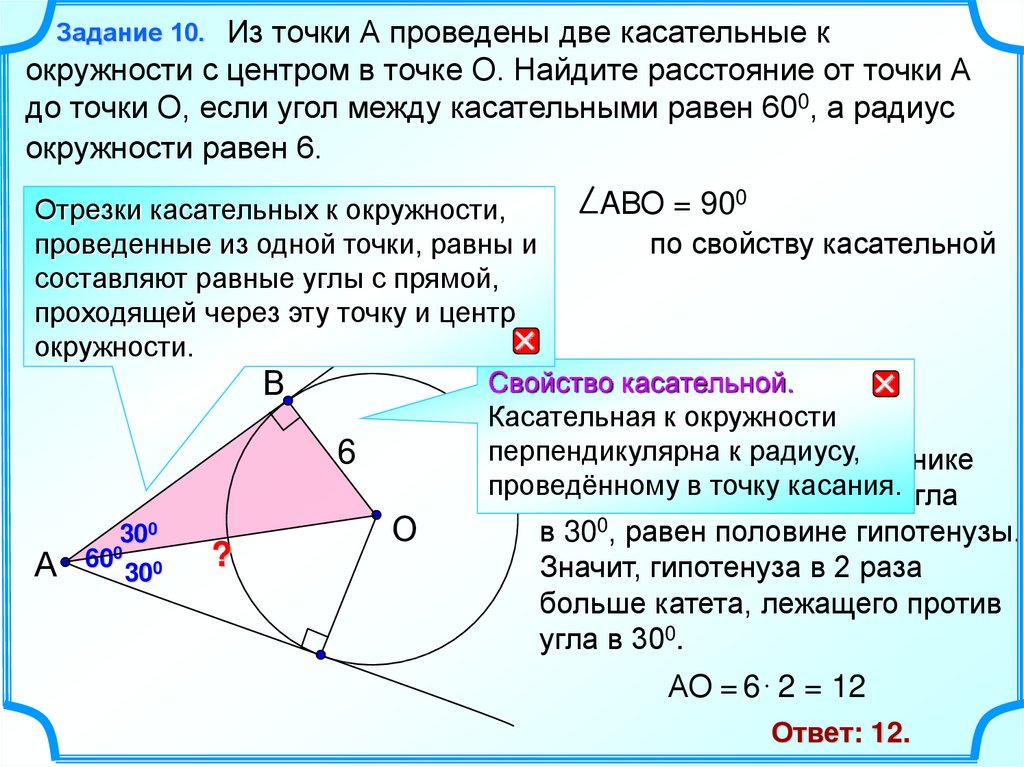
10.

Из точки А проведены две касательные к
окружности с центром в точке О. Найдите расстояние от точки А
до точки О, если угол между касательными равен 600, а радиус
окружности равен 6.
Задание 10.
0
AВО = 90
Отрезки касательных к окружности,
проведенные из одной точки, равны и
по свойству касательной
составляют равные углы с прямой,
проходящей через эту точку и центр
окружности.
Cвойство касательной.
В
Касательная к окружности
перпендикулярна
к радиусу,
6
В прямоугольном
треугольнике
проведённому
в точку
касания.угла
катет, лежащий
напротив
О
в 300, равен половине гипотенузы.
300
0
А 60 300 ?
Значит, гипотенуза в 2 раза
больше катета, лежащего против
угла в 300.
АО = 6 2 = 12
Ответ: 12.

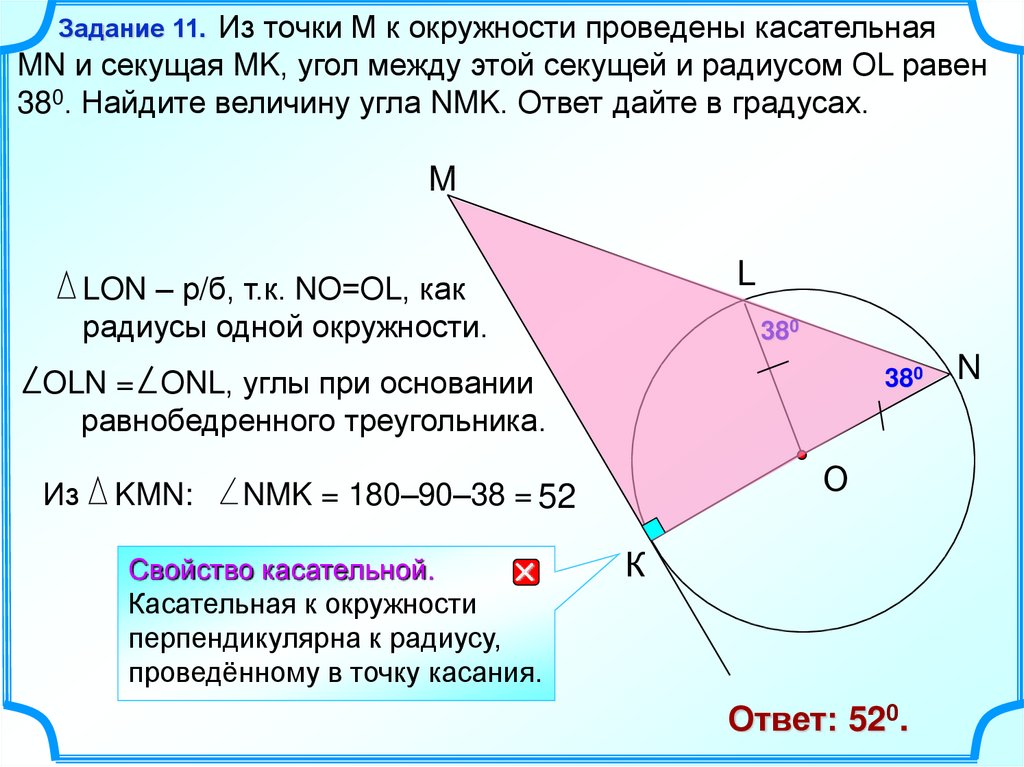
11.

Из точки М к окружности проведены касательная
MN и секущая MK, угол между этой секущей и радиусом ОL равен
380. Найдите величину угла NMK. Ответ дайте в градусах.
Задание 11.
M
L
LON – р/б, т.к. NО=ОL, как
радиусы одной окружности.
380
OLN = ОNL, углы при основании
равнобедренного треугольника.
Из
KMN:
380
О
NMK = 180–90–38 = 52
Cвойство касательной.
Касательная к окружности
перпендикулярна к радиусу,
проведённому в точку касания.
К
Ответ: 520.
N

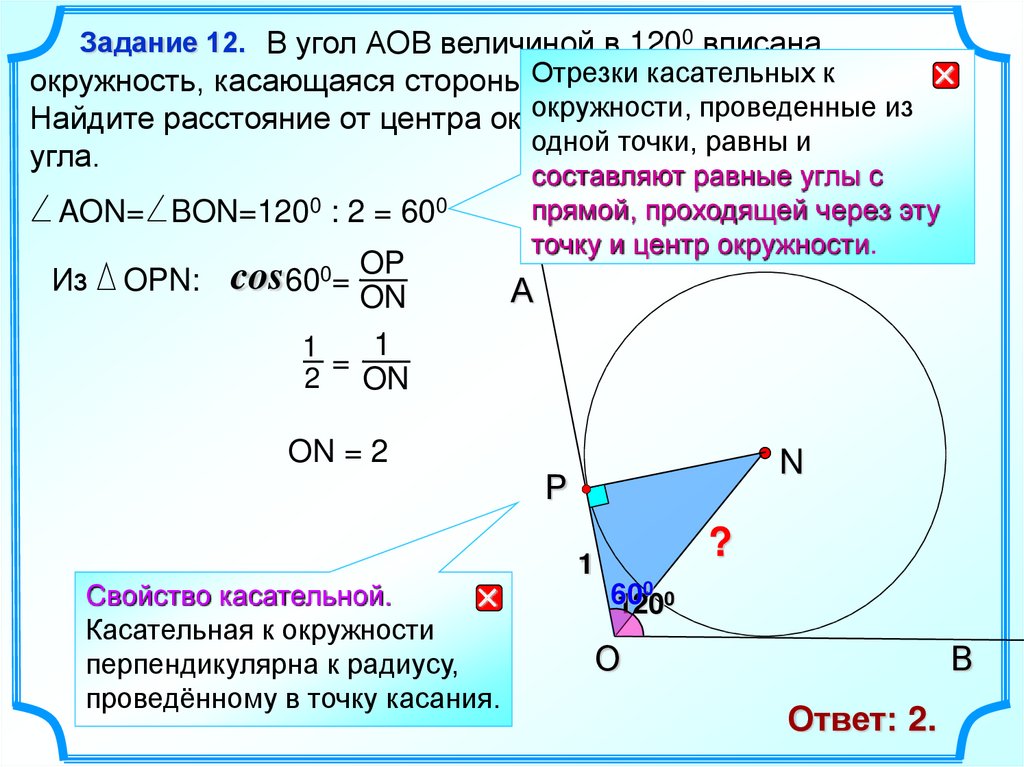
12.

Задание 12. В угол АОВ величиной в 1200 вписана
касательных
к ОР=1.
окружность, касающаяся стороны Отрезки
ОА в точке
P, причём
окружности,
из
Найдите расстояние от центра окружности
допроведенные
вершины этого
одной точки, равны и
угла.
составляют равные углы с
прямой, проходящей через эту
AON= BON=1200 : 2 = 600
точку и центр окружности.
Из
OPN:
cos600= OP
ON
А
1
1
=
2 ON
ON = 2
Cвойство касательной.
Касательная к окружности
перпендикулярна к радиусу,
проведённому в точку касания.
N
Р
?
1
0
60
1200
О
В
Ответ: 2.

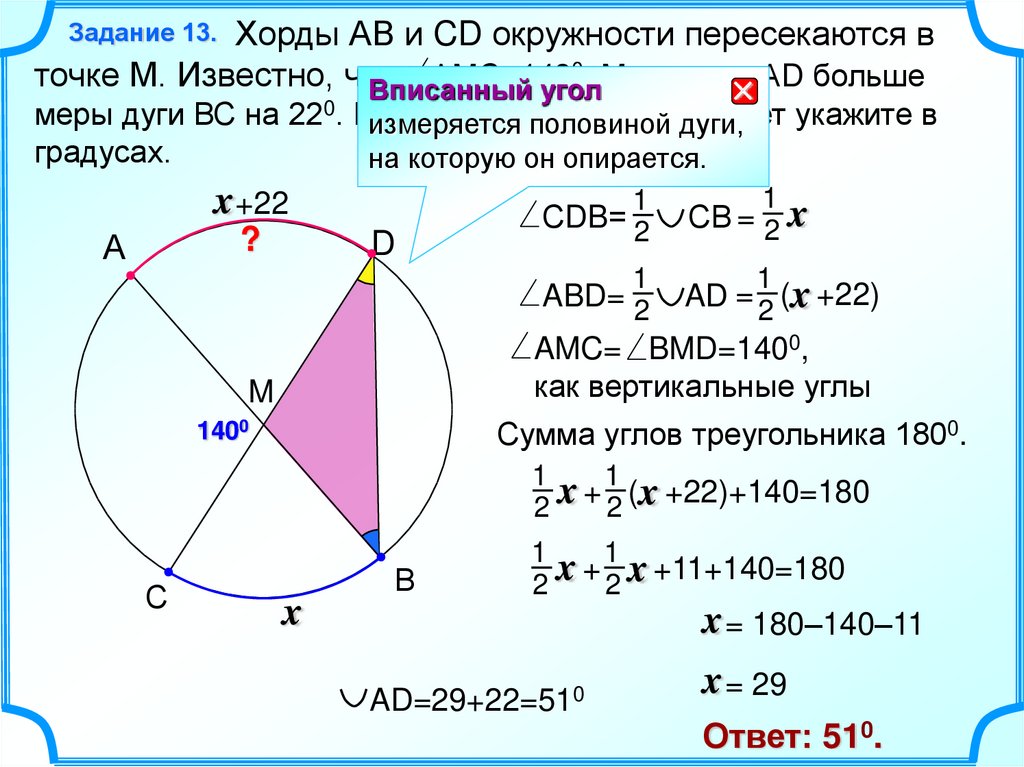
13.

Хорды АВ и CD окружности пересекаются в
0. Мера дуги АD больше
точке М. Известно, что
АМС=140
Вписанный угол
Задание 13.
меры дуги ВС на 220. Найдите
меру
дуги АD.дуги,
Ответ укажите в
измеряется
половиной
градусах.
на которую он опирается.
x +22
?
А
D
1
СDB= 2
1
СВ = 2 x
1
ABD= 2
AD = 2 (x +22)
1
AMC= BMD=1400,
как вертикальные углы
M
Сумма углов треугольника 1800.
1400
1
1
+
( +22)+140=180
x
2
2 x
С
x
В
1
1
+
+11+140=180
x
2
2x
x = 180–140–11
AD=29+22=510
x = 29
Ответ: 510.

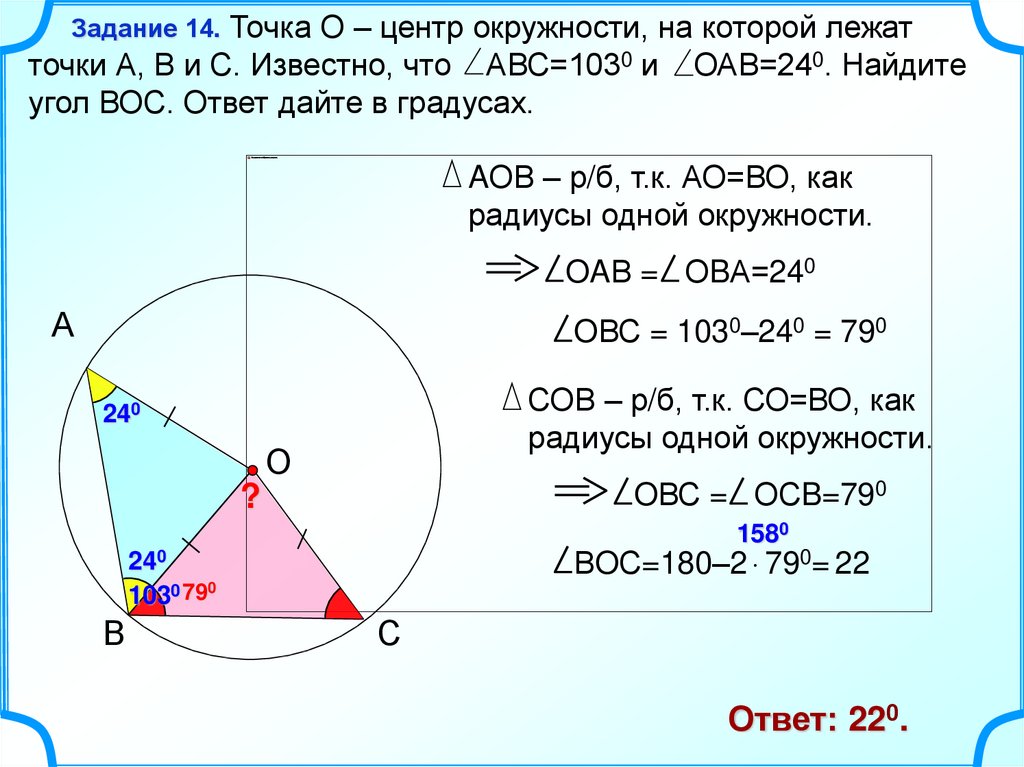
14.

Точка О – центр окружности, на которой лежат
точки А, В и С. Известно, что АВС=1030 и ОАВ=240. Найдите
угол ВОС. Ответ дайте в градусах.
Задание 14.
AОВ – р/б, т.к. АО=ВО, как
радиусы одной окружности.
OAВ = ОBА=240
А
OВС = 1030–240 = 790
СОВ – р/б, т.к. СО=ВО, как
радиусы одной окружности.
240
О
OВС = ОСB=790
?
1580
ВOС=180–2 790= 22
240
1030 790
В
С
Ответ: 220.

15.

Задание 15. Точка
О – центр окружности, на которой лежат
точки А, В и С. Известно, что АВС=750 и ОАВ=430.
Найдите угол ВСО. Ответ дайте в градусах.
AОВ – р/б, т.к. АО=ВО, как
радиусы одной окружности.
А
OAВ = ОBА=430
430
OВС = 750 – 430 = 320
О
430
0
0 32
В
75
СОВ – р/б, т.к. СО=ВО, как
радиусы одной окружности.
?
С
OВС = ОСB=320
Ответ: 320.

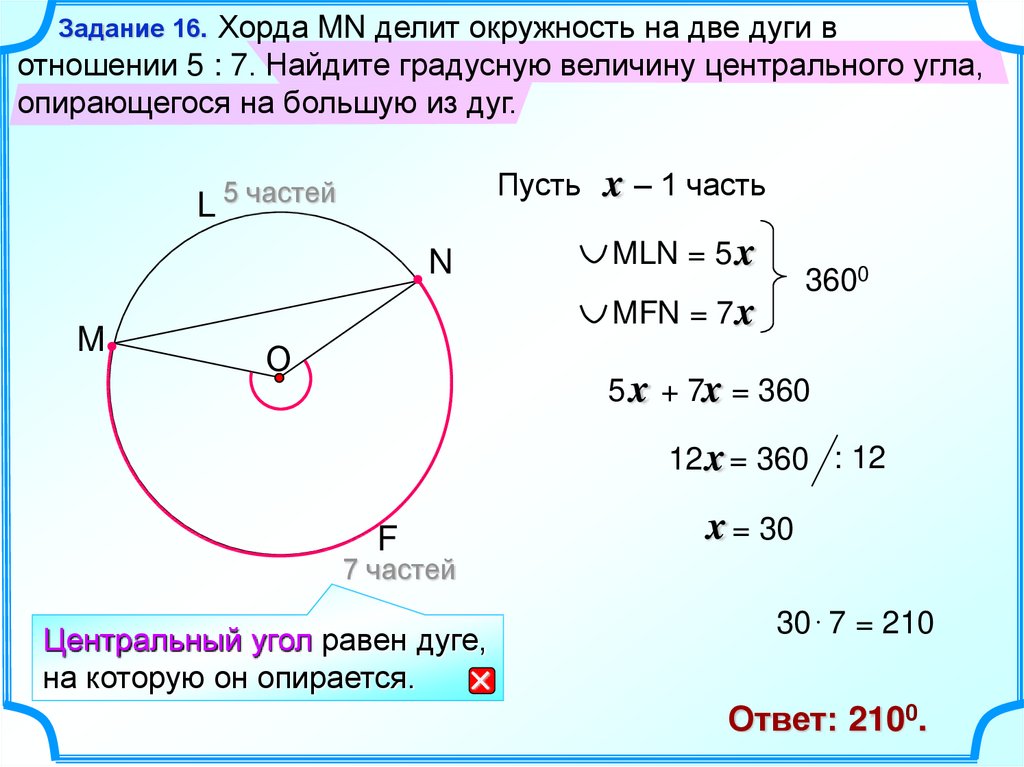
16.

Хорда MN делит окружность на две дуги в
отношении 5 : 7. Найдите градусную величину центрального угла,
опирающегося на большую из дуг.
Задание 16.
Пусть
L 5 частей
N
M
x – 1 часть
MLN = 5 x
3600
MFN = 7 x
О
5 x + 7x = 360
12 x = 360 : 12
F
x = 30
7 частей
Центральный угол равен дуге,
на которую он опирается.
30 7 = 210
Ответ: 2100.

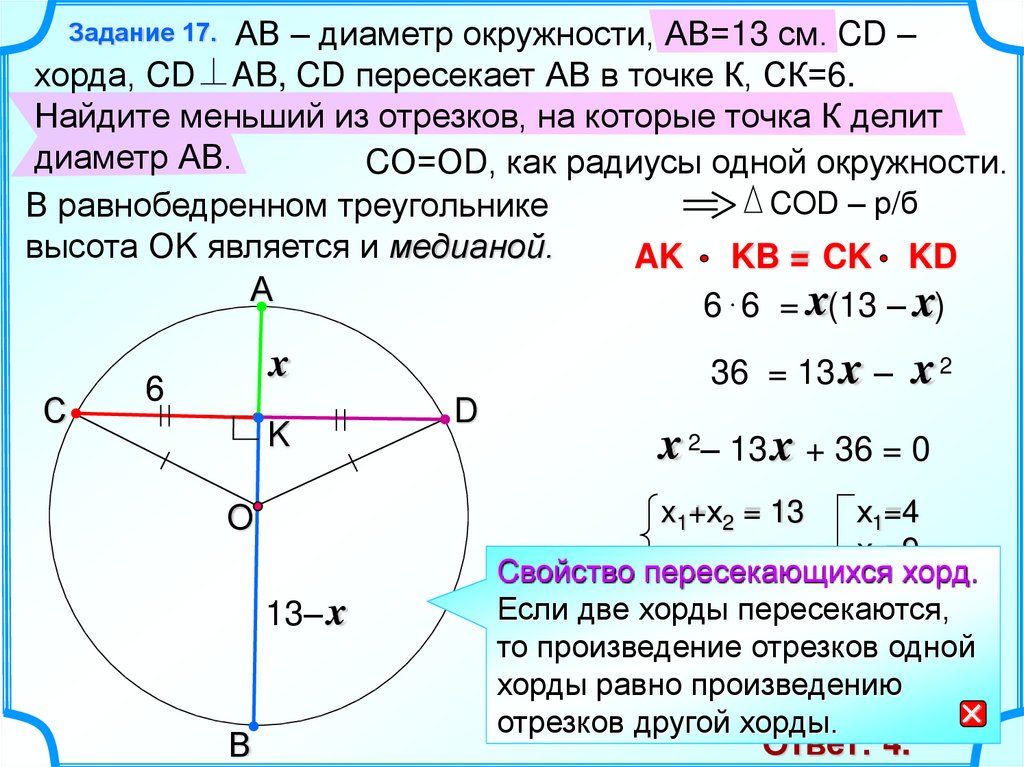
17.

АВ – диаметр окружности, АВ=13 см. CD –
хорда, CD AB, CD пересекает АВ в точке К, СК=6.
Найдите меньший из отрезков, на которые точка К делит
диаметр АВ.
CО=ОD, как радиусы одной окружности.
CОD – р/б
В равнобедренном треугольнике
высота ОK является и медианой.
AK KB = CK KD
А
6 6 = x(13 – x)
Задание 17.
С
x
6
K
D
13– x
x2
x 2– 13 x + 36 = 0
х1=4
х2=9
х2 = 36
x
1
Cвойство пересекающихся хорд.
Если две хорды пересекаются,
то произведение отрезков одной
хорды равно произведению
отрезков другой хорды.
x1+х2 = 13
O
В
36 = 13 x –
Ответ: 4.

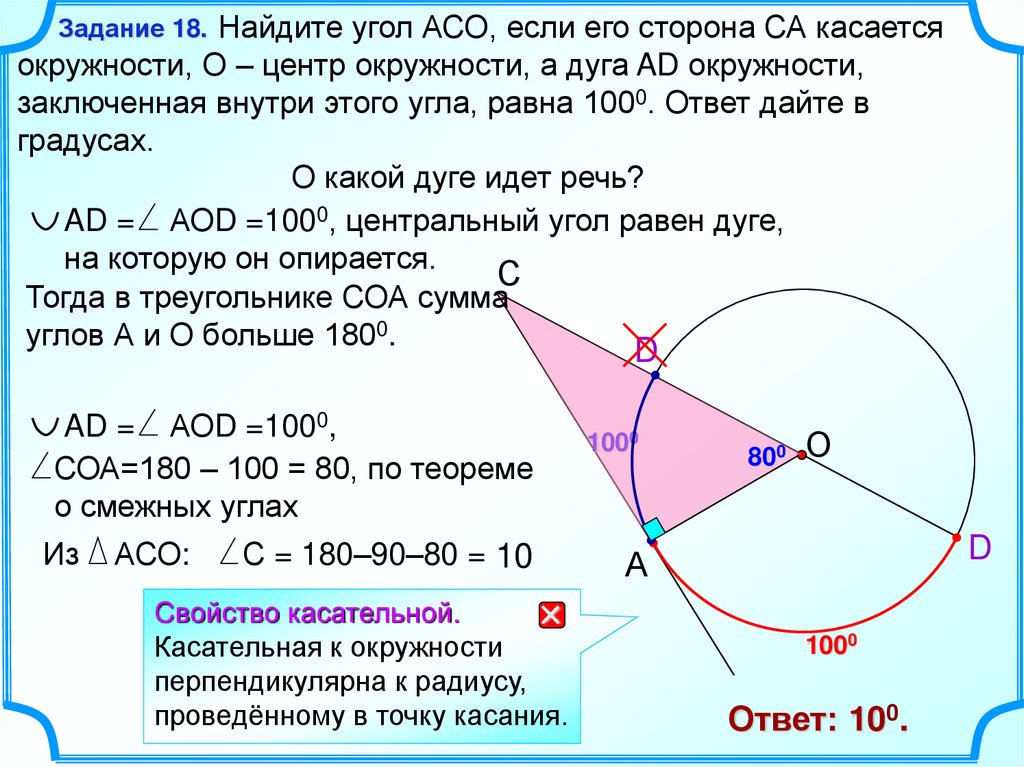
18.

Найдите угол АСО, если его сторона СА касается
окружности, О – центр окружности, а дуга AD окружности,
заключенная внутри этого угла, равна 1000. Ответ дайте в
градусах.
О какой дуге идет речь?
AD = АОD =1000, центральный угол равен дуге,
на которую он опирается.
С
Тогда в треугольнике СОА сумма
углов А и О больше 1800.
Задание 18.
D
AD = АОD =1000,
СОА=180 – 100 = 80, по теореме
о смежных углах
Из
АСО:
С = 180–90–80 = 10
Cвойство касательной.
Касательная к окружности
перпендикулярна к радиусу,
проведённому в точку касания.
1000
800
О
D
А
1000
Ответ: 100.

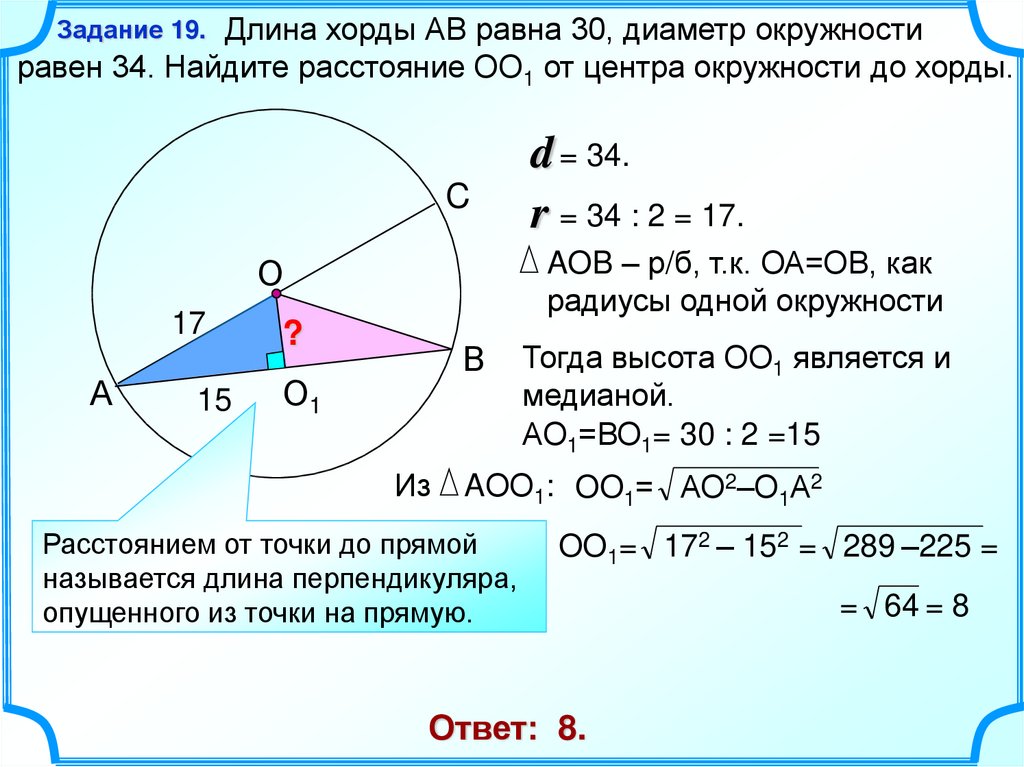
19.

Длина хорды АВ равна 30, диаметр окружности
равен 34. Найдите расстояние ОО1 от центра окружности до хорды.
Задание 19.
C
AOB – р/б, т.к. ОА=ОВ, как
радиусы одной окружности
О
17
А
15
d = 34.
r = 34 : 2 = 17.
?
В
О1
Из
Тогда высота ОО1 является и
медианой.
АО1=ВО1= 30 : 2 =15
AОО1: OO1= АО2–О1А2
Расстоянием от точки до прямой
называется длина перпендикуляра,
опущенного из точки на прямую.
OO1= 172 – 152 = 289 –225 =
Ответ: 8.
= 64 = 8

20.

На рисунке
MP= KQ = 1300 и
N. Ответ дайте в градусах.
Задание 20.
Найдите
MK=900.
PQ = 360 – 130 2 – 90 = 10
900
M
K
O
1300
Угол между двумя секущими
(вне окружности),
1
N
=
MK–точки,
PQ)
проведенными 2
из( одной
измеряется полуразностью
80
1
N =внутри
(90–10)
= 40
заключенных
его дуг.
2
1300
1
E = 2( DC– AB)
P
100
Q
A
E
D
B
C
N
Ответ: 40.

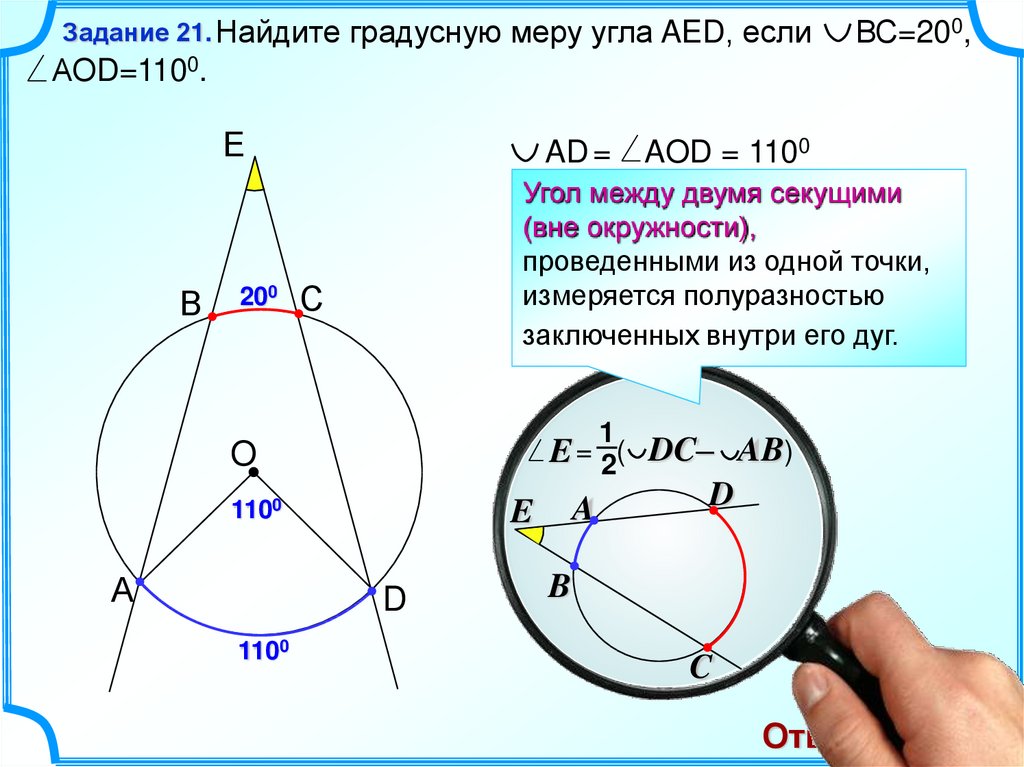
21.

Задание 21. Найдите
градусную меру угла AED, если
ВС=200,
АОD=1100.
Е
В
200
AD =
Угол между двумя секущими
1
(вне окружности),
E = ( AD– BC)
2 из одной точки,
проведенными
90
измеряется1полуразностью
E = (110–20) = 45
2 внутри его дуг.
заключенных
С
1
E = 2( DC– AB)
O
1100
А
A
E
D
1100
AOD = 1100
D
B
C
Ответ: 45.