Похожие презентации:
Окружность и круг. Угол между касательной и хордой
1.
2. Окружность. Круг.
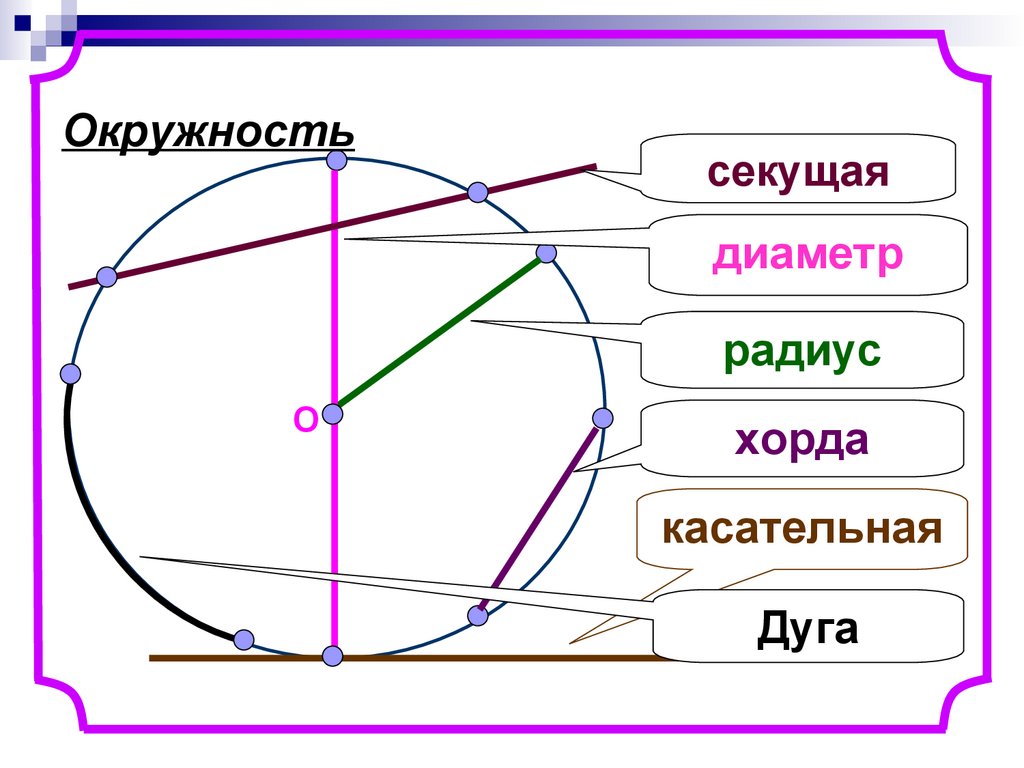
3. Окружность
секущаядиаметр
радиус
О
хорда
касательная
Дуга
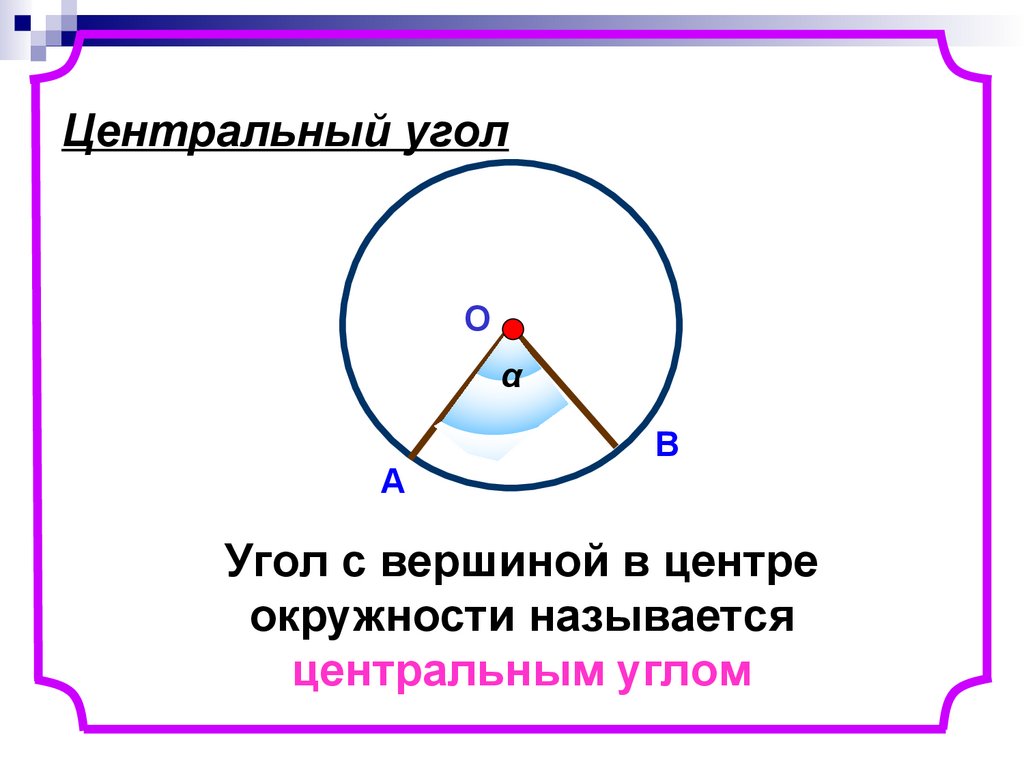
4. Центральный угол
Оα
А
В
Угол с вершиной в центре
окружности называется
центральным углом
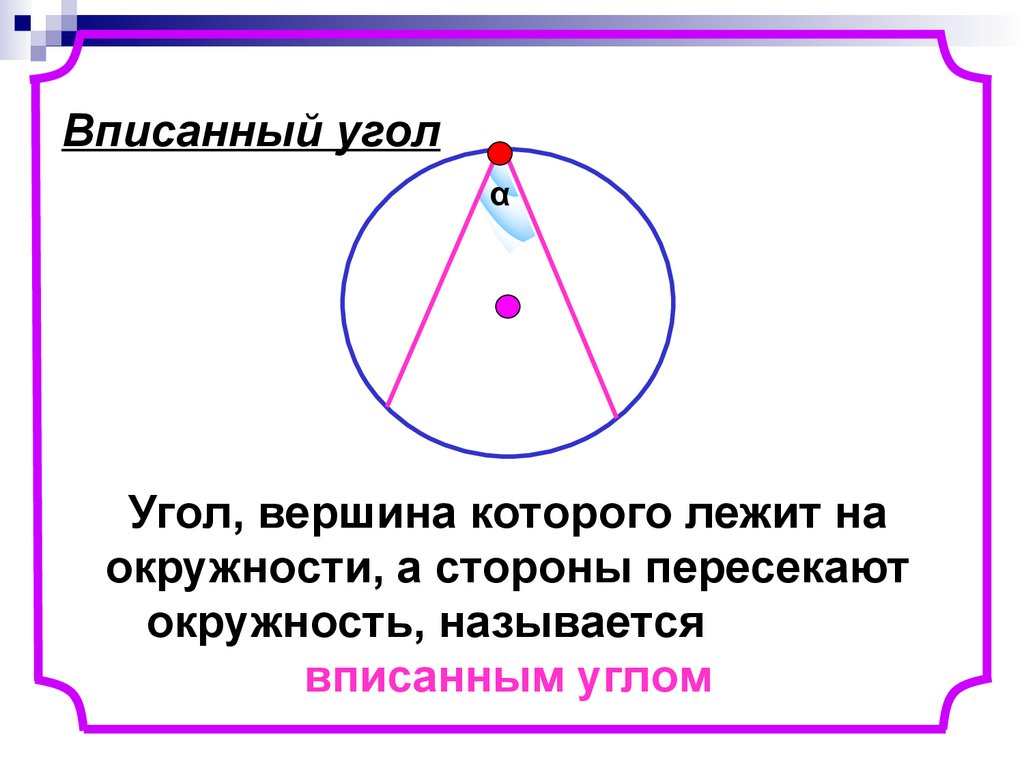
5. Вписанный угол
αУгол, вершина которого лежит на
окружности, а стороны пересекают
окружность, называется
вписанным углом
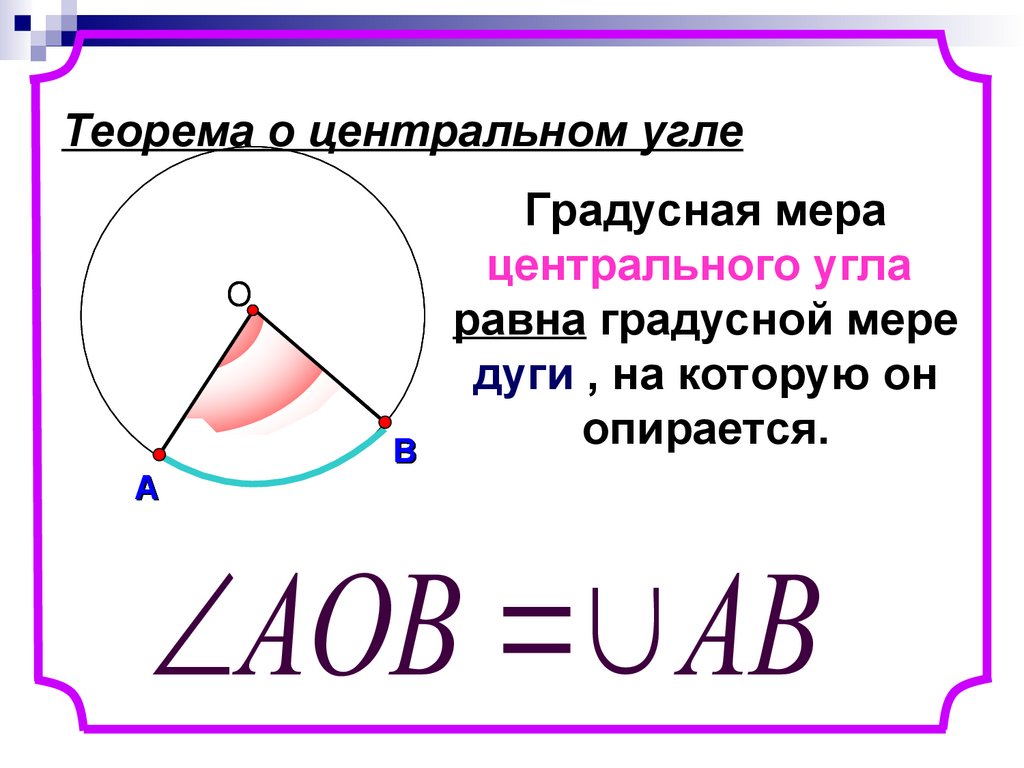
6. Теорема о центральном угле
ОА
В
Градусная мера
центрального угла
равна градусной мере
дуги , на которую он
опирается.
AOB AB
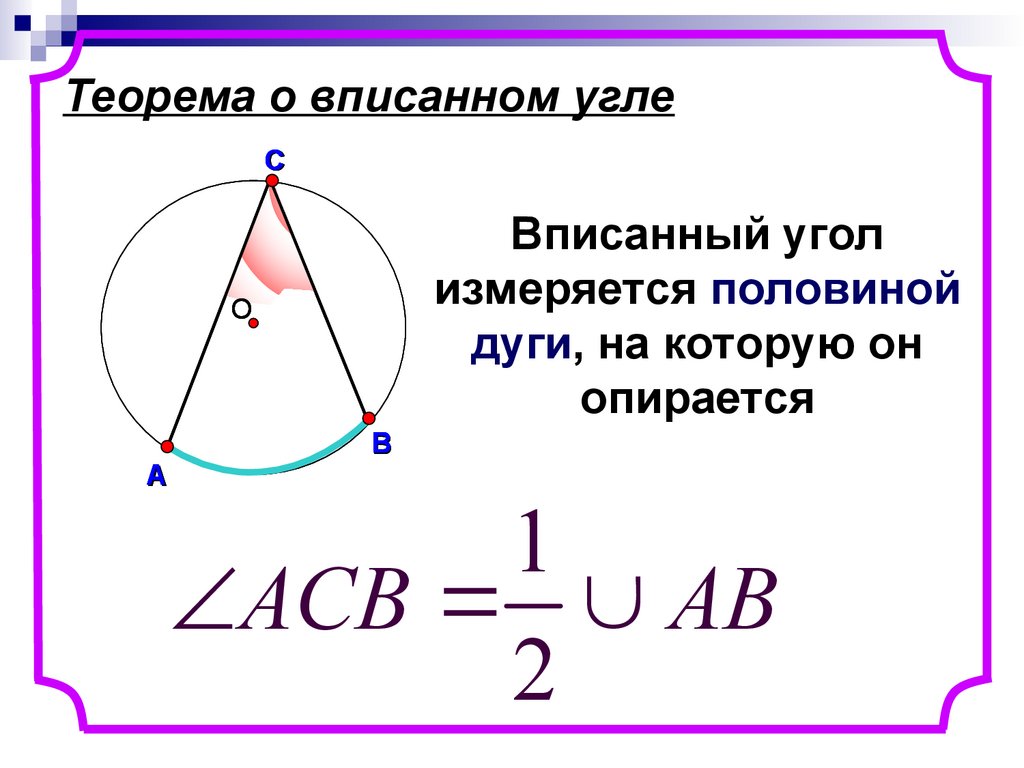
7. Теорема о вписанном угле
СВписанный угол
измеряется половиной
дуги, на которую он
опирается
О
А
В
1
ACB AB
2
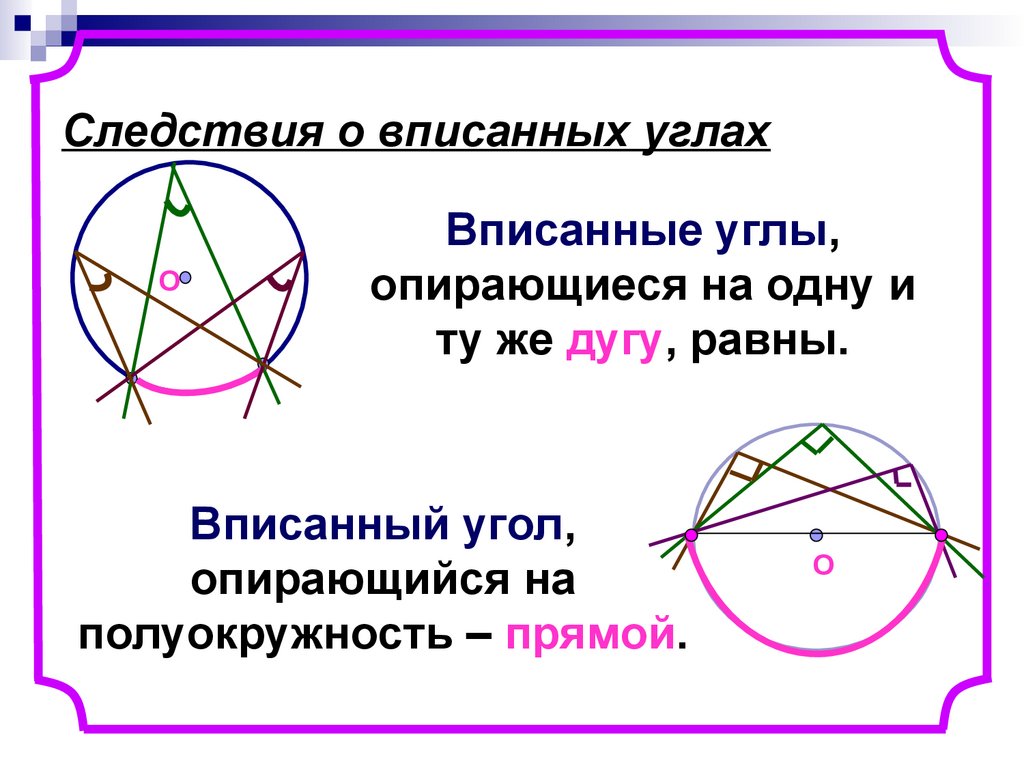
8. Следствия о вписанных углах
ОВписанные углы,
опирающиеся на одну и
ту же дугу, равны.
Вписанный угол,
опирающийся на
полуокружность – прямой.
О
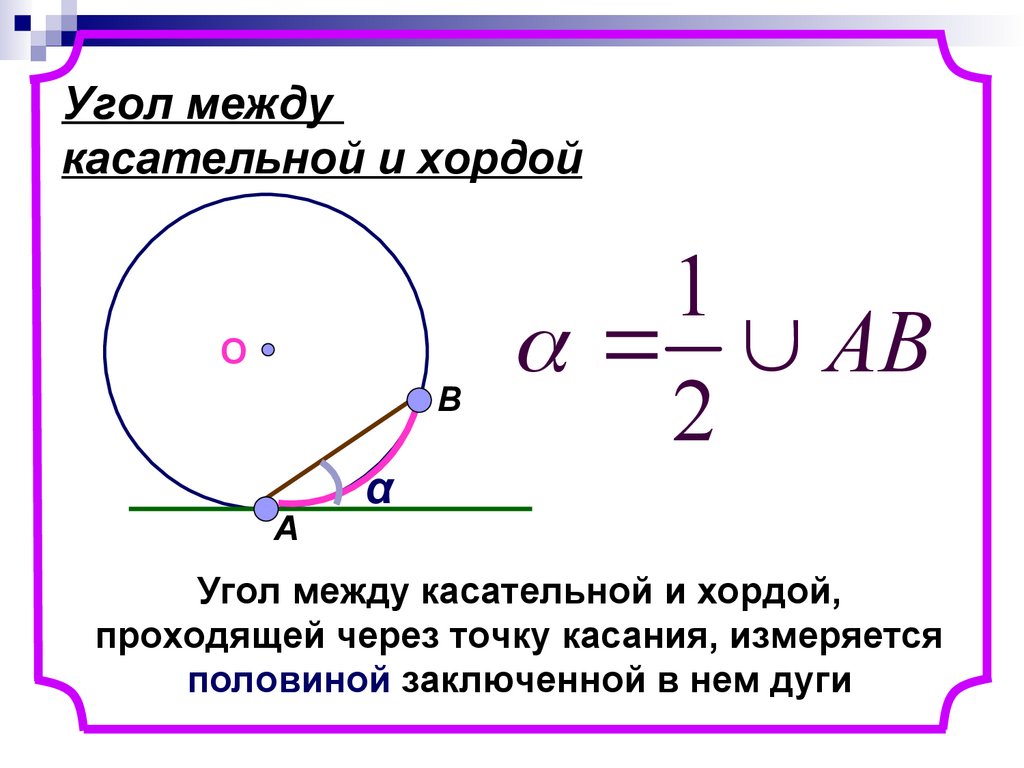
9. Угол между касательной и хордой
ОВ
А
1
AB
2
α
Угол между касательной и хордой,
проходящей через точку касания, измеряется
половиной заключенной в нем дуги
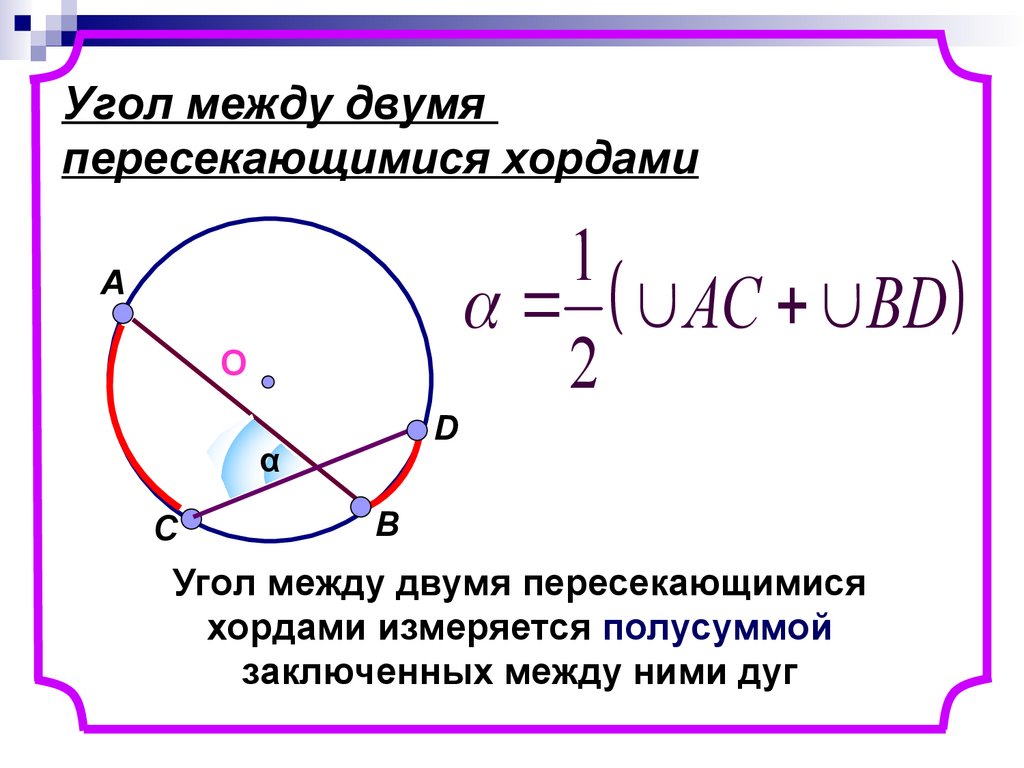
10. Угол между двумя пересекающимися хордами
1AC BD
2
А
О
D
α
С
В
Угол между двумя пересекающимися
хордами измеряется полусуммой
заключенных между ними дуг
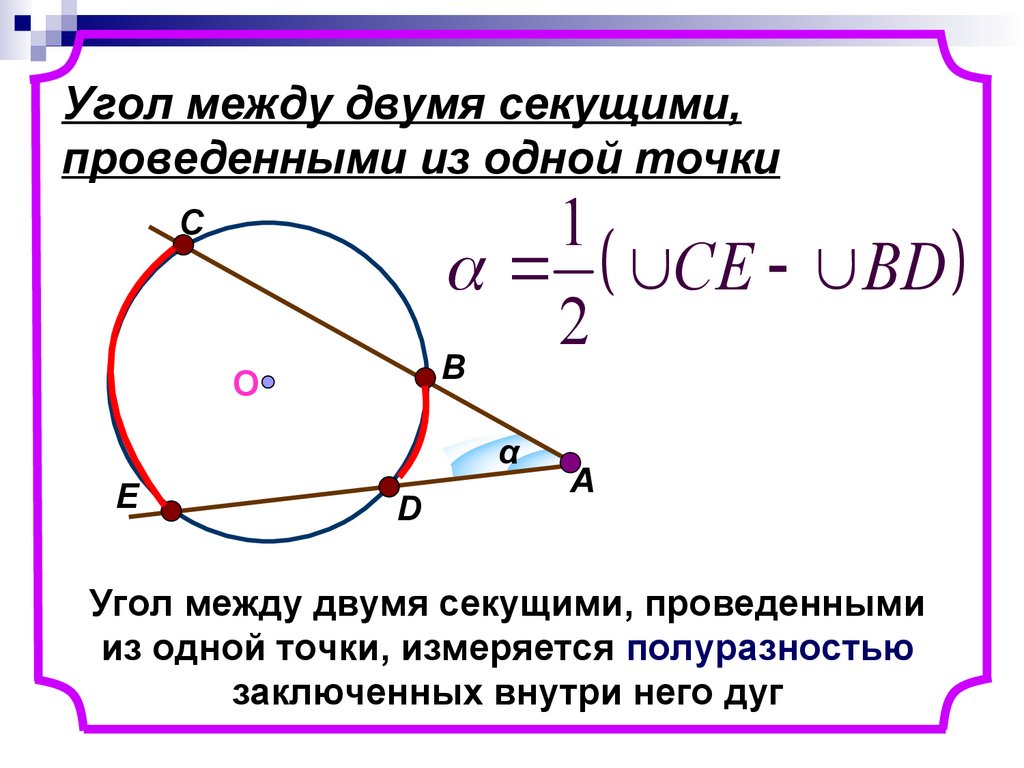
11. Угол между двумя секущими, проведенными из одной точки
1CE BD
2
B
C
О
α
E
D
А
Угол между двумя секущими, проведенными
из одной точки, измеряется полуразностью
заключенных внутри него дуг
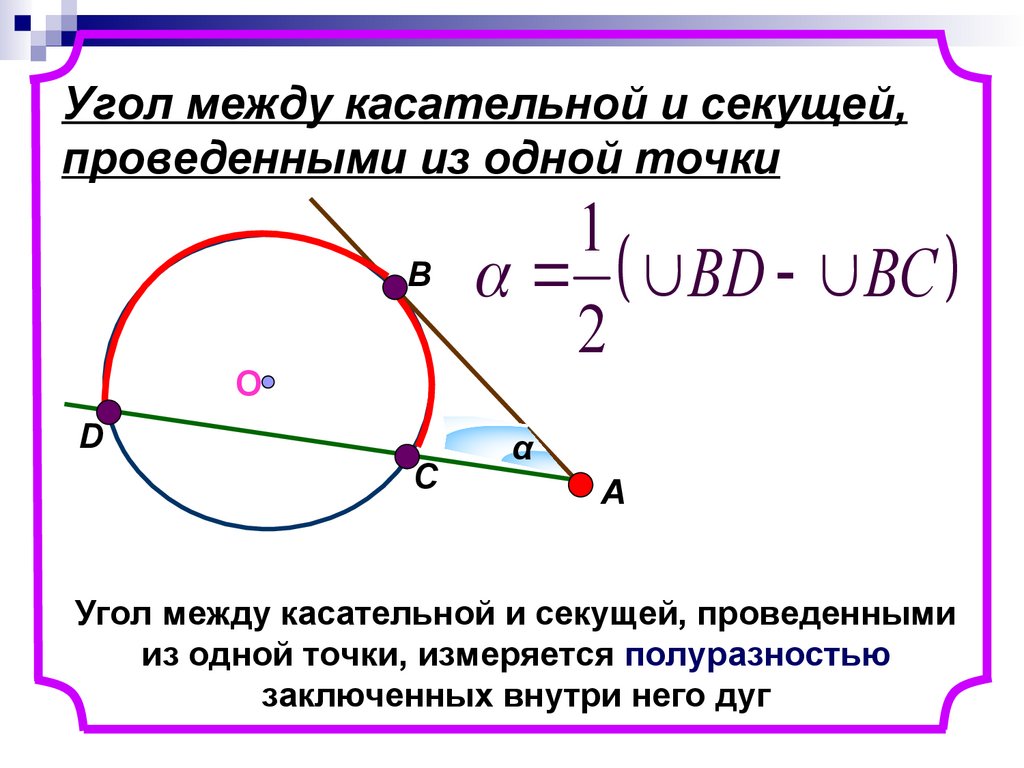
12. Угол между касательной и секущей, проведенными из одной точки
BО
D
C
1
BD BC
2
α
A
Угол между касательной и секущей, проведенными
из одной точки, измеряется полуразностью
заключенных внутри него дуг
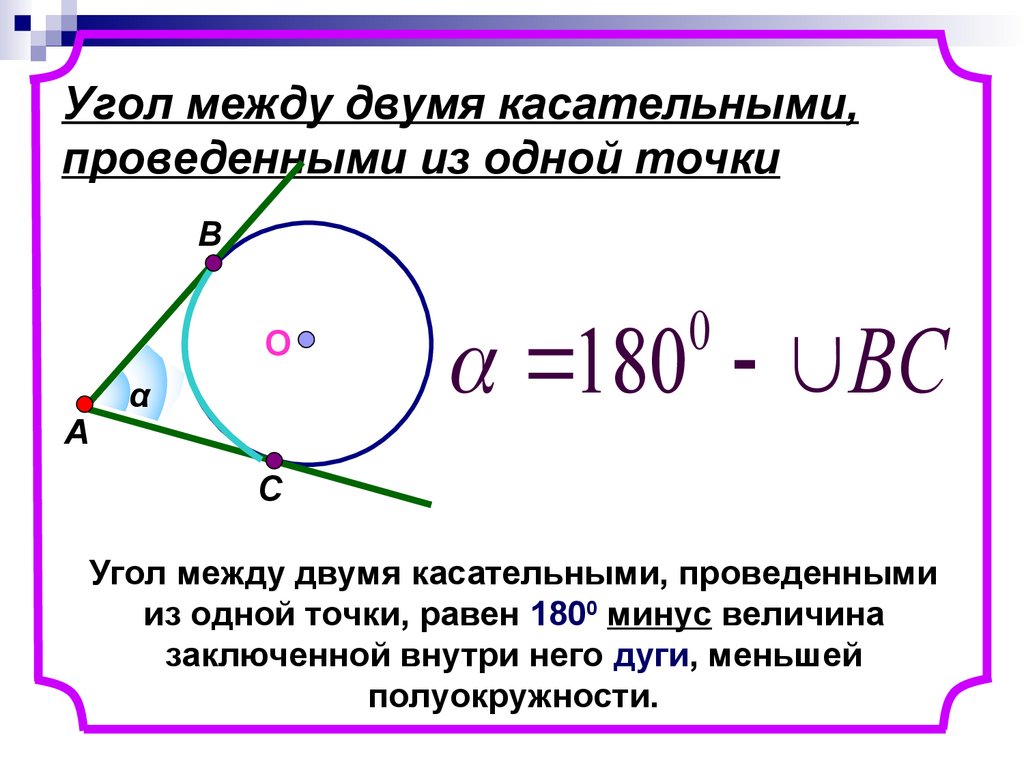
13. Угол между двумя касательными, проведенными из одной точки
BО
A
α
0
180 BC
C
Угол между двумя касательными, проведенными
из одной точки, равен 1800 минус величина
заключенной внутри него дуги, меньшей
полуокружности.
14.
15
9
13
17
21
25
29
2
6
10
14
18
22
26
30
3
7
11
15
19
23
27
31
4
8
12
16
20
24
28
Литература
15.
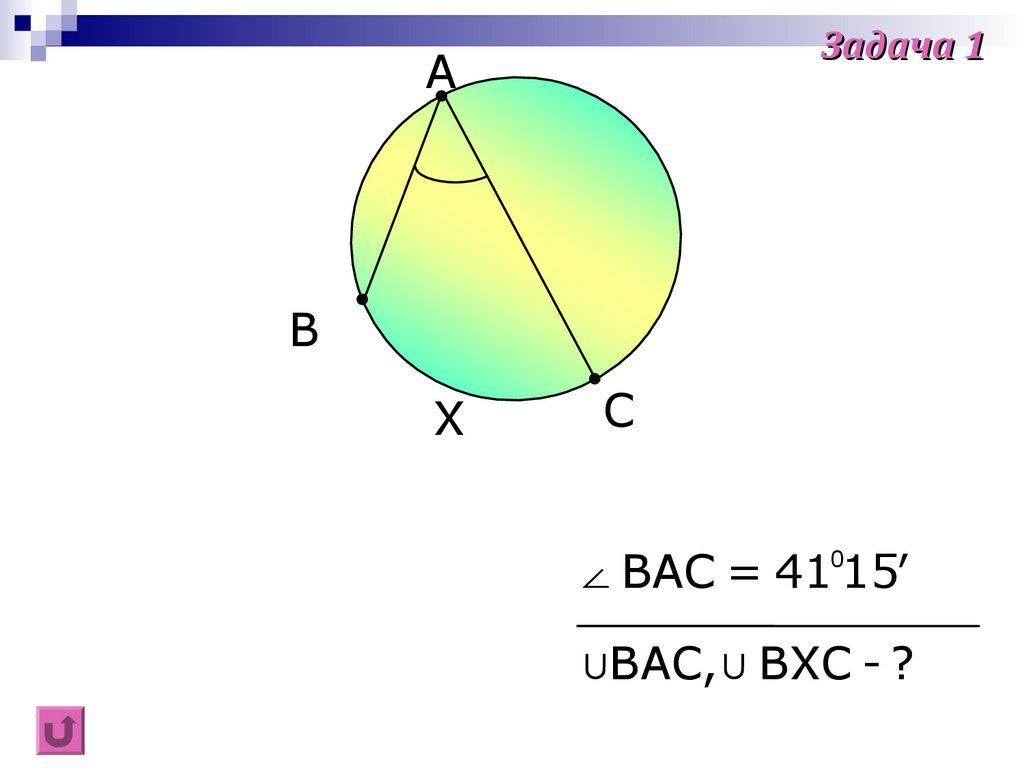
Задача 1A
B
X
C
∠ BAC = 41 15′
0
∪BAC,∪ BXC - ?
16.
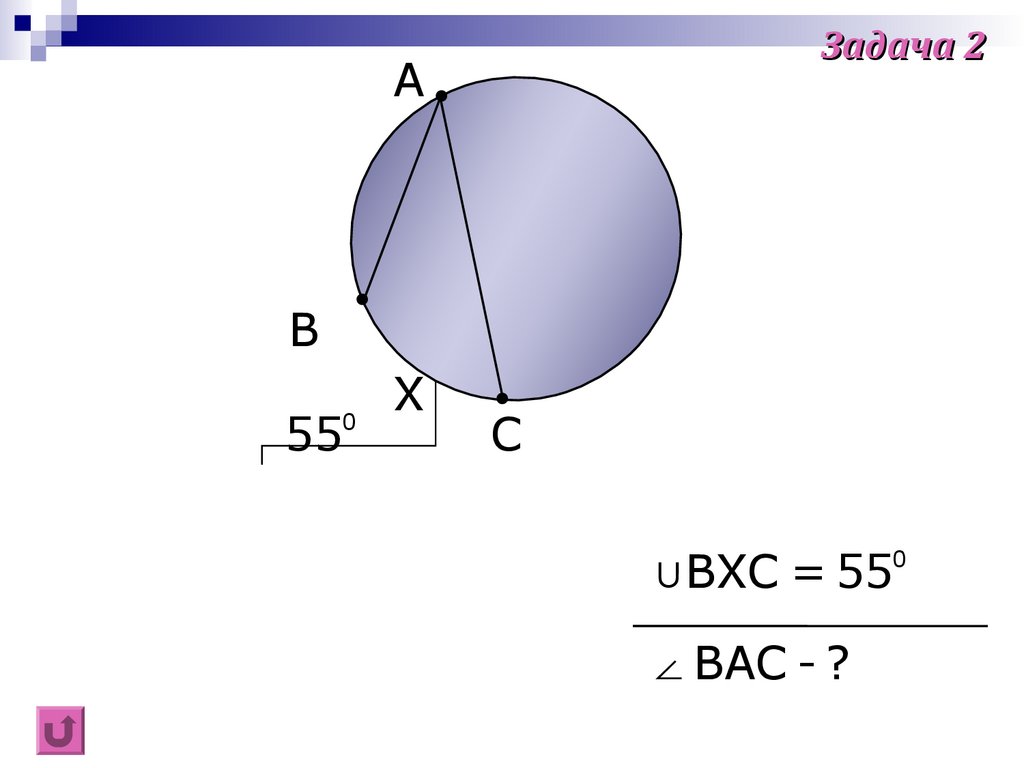
Задача 2A
B
55
0
X
C
∪BXC = 55
0
∠ BAC - ?
17.
Задача 3A
C
B
О
∠ BAC - ?
18.
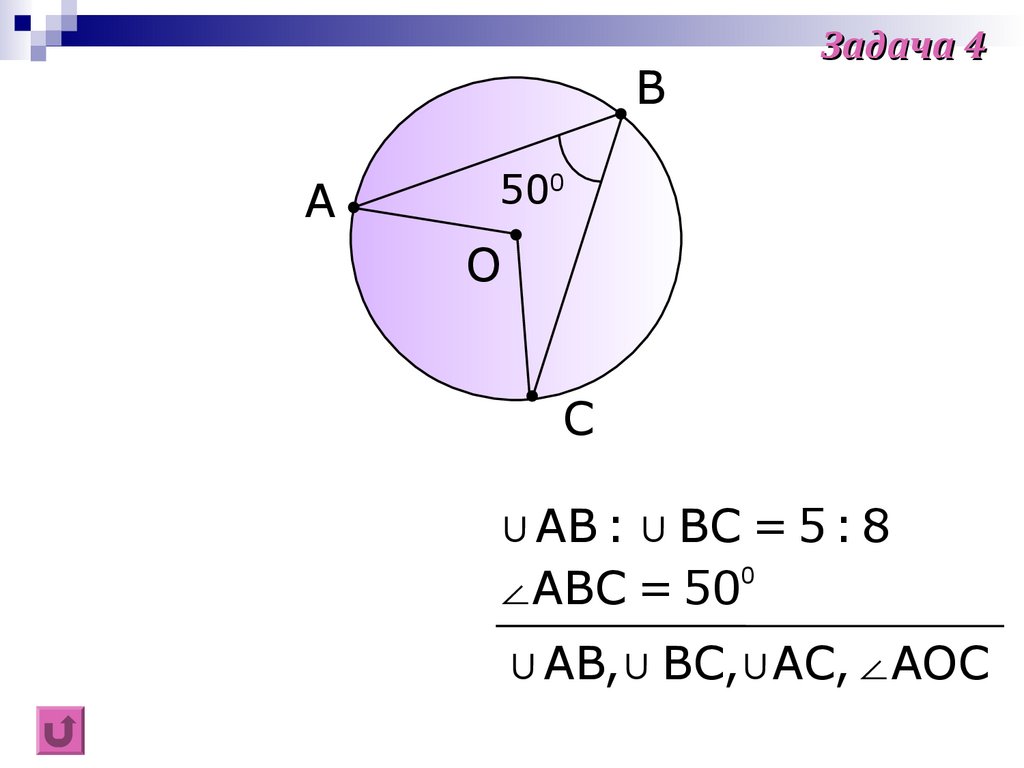
BA
Задача 4
500
O
C
∪AB : ∪ BC = 5 : 8
0
∠ABC = 50
∪AB,∪ BC,∪AC,∠AOC
19.
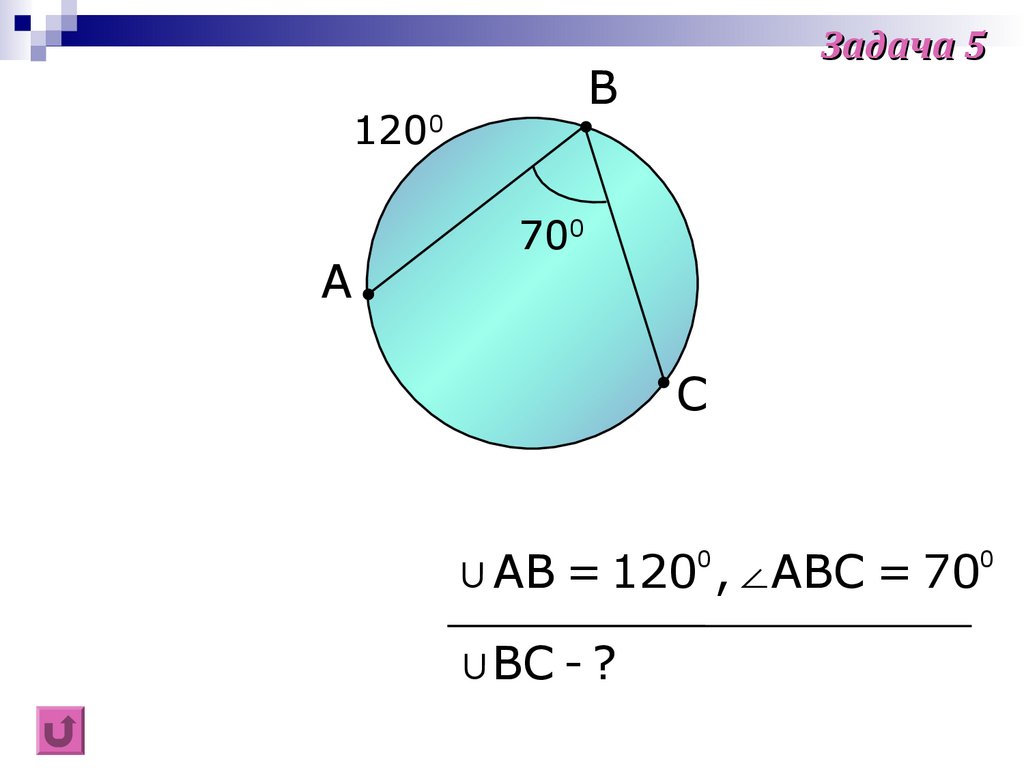
B1200
A
Задача 5
700
C
∪AB = 120 ,∠ABC = 70
0
∪BC - ?
0
20.
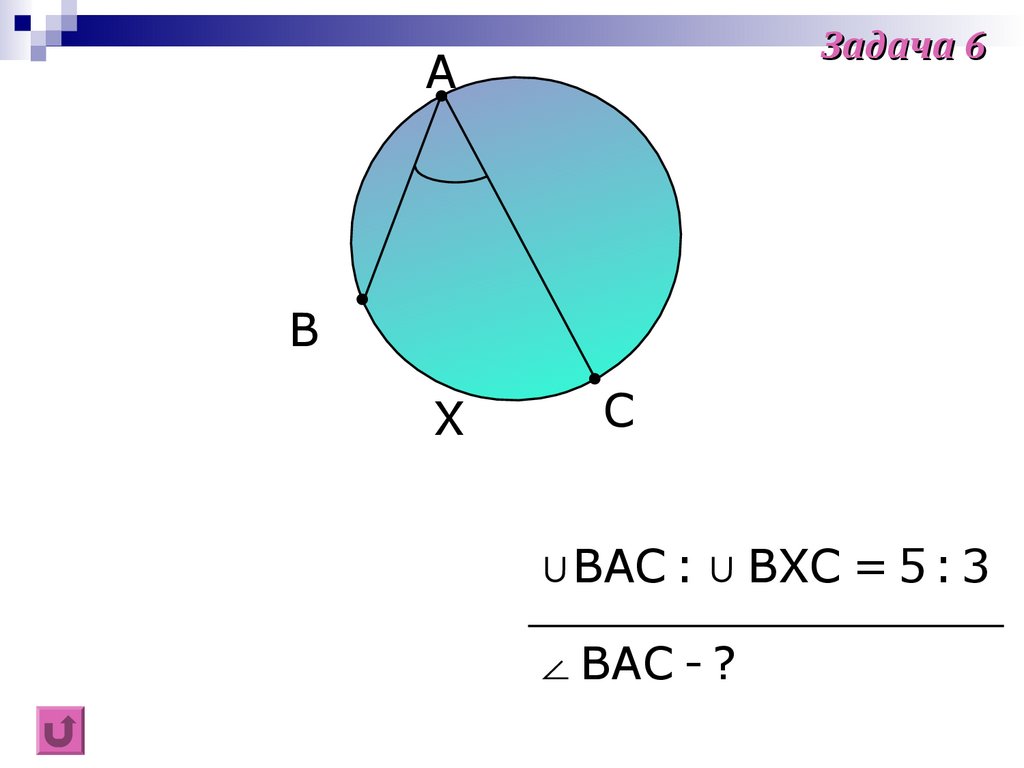
Задача 6A
B
X
C
∪BAC : ∪ BXC = 5 : 3
∠ BAC - ?
21.
AB
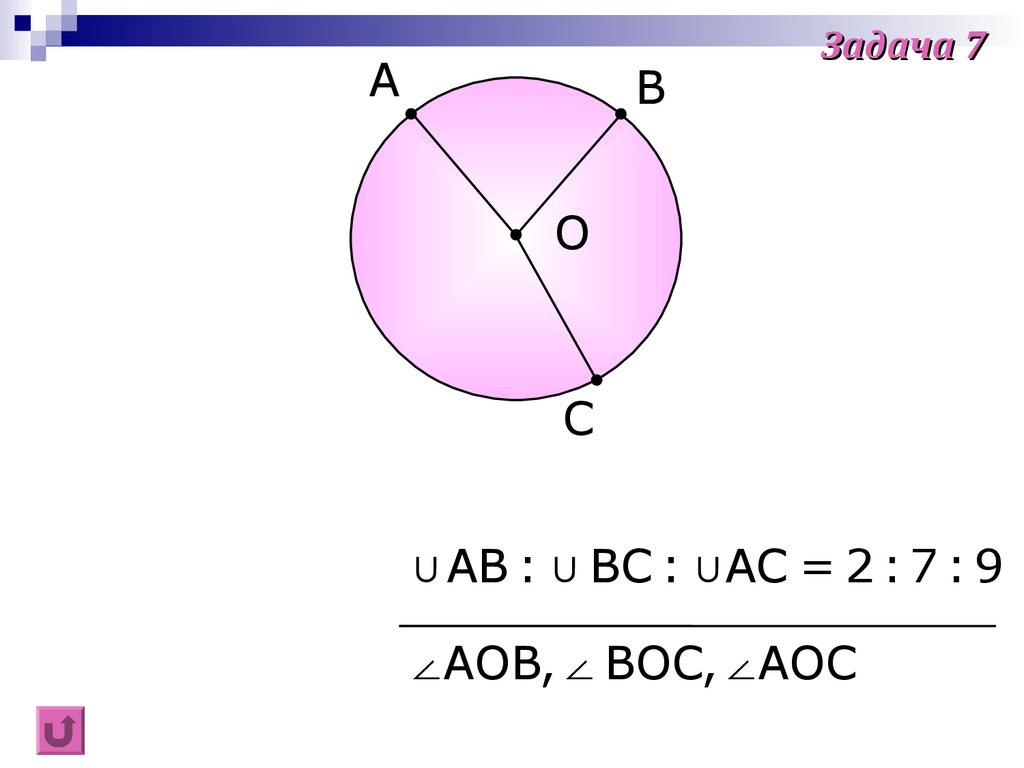
Задача 7
O
C
∪AB : ∪ BC : ∪AC = 2 : 7 : 9
∠AOB,∠ BOC,∠AOC
22.
Задача 8A
B
O
C
AB = AO
∠ CAB - ?
23.
Задача 9B
A
C
∪AB : ∪ BC : ∪AC = 5 : 6 : 7
∠ACB,∠ BAC,∠ ABC - ?
24.
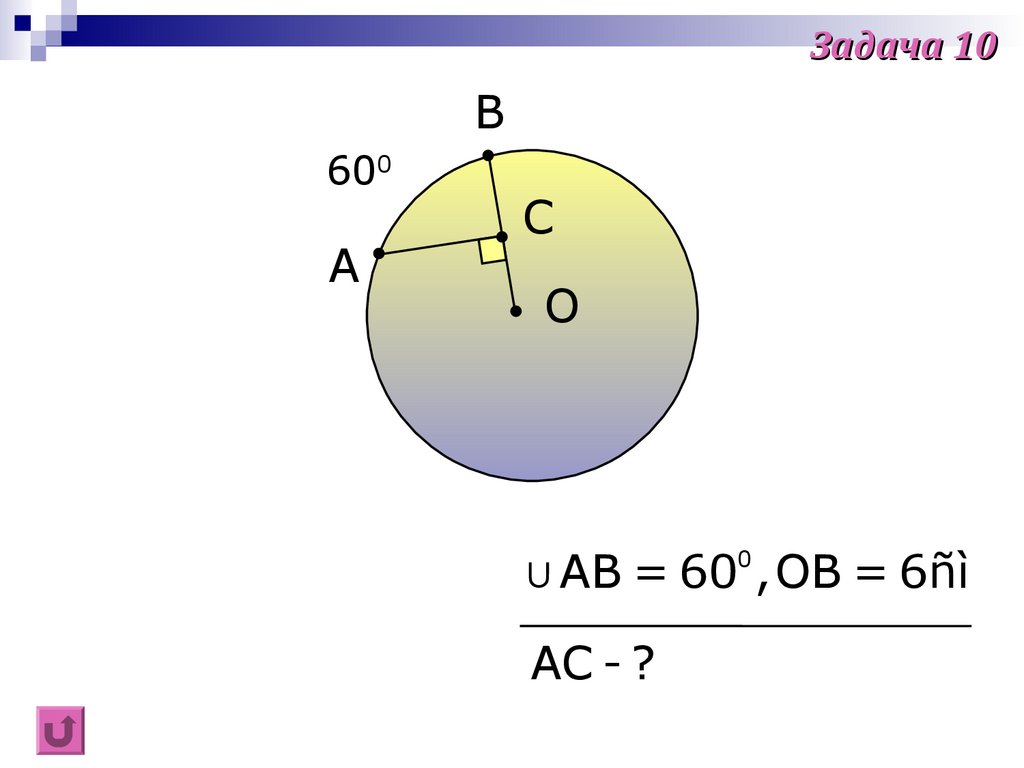
Задача 10B
600
A
C
O
∪AB = 60 , OB = 6ñì
0
AC - ?
25.
Задача 11С
56
0
О
A
В
∠CAB - ?
26.
Задача 12A
230
С
О
В
∠COB - ?
27.
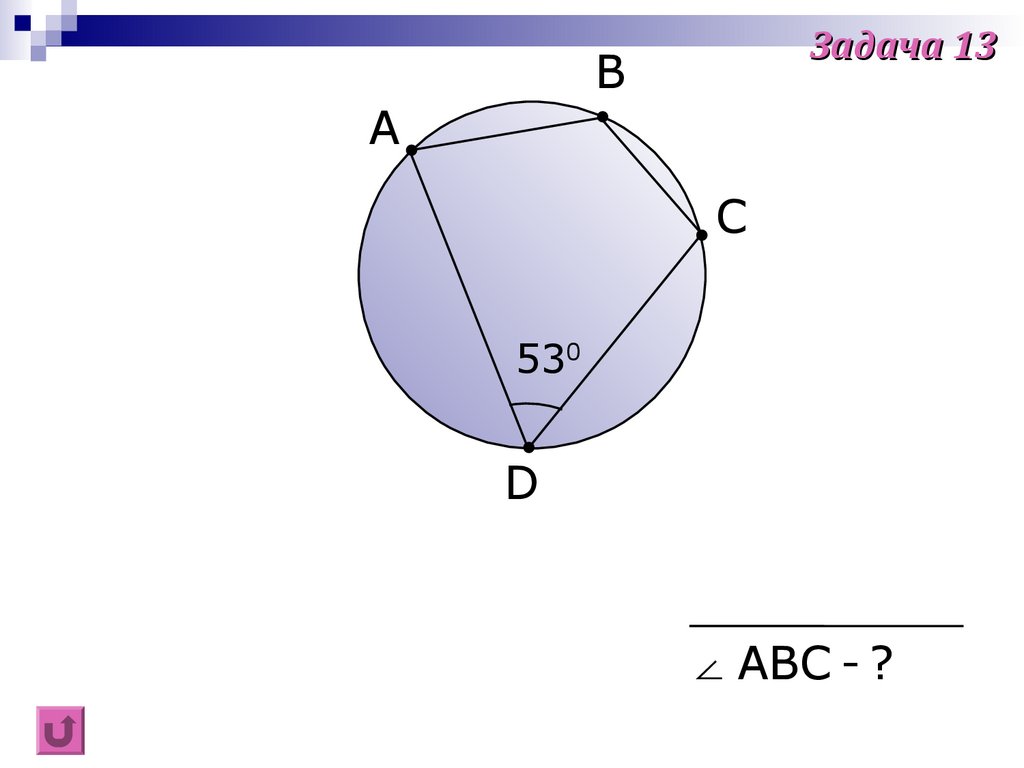
Задача 13B
A
C
530
D
∠ ABC - ?
28.
Задача 14B
A
1250
C
O
∠ ABC - ?
29.
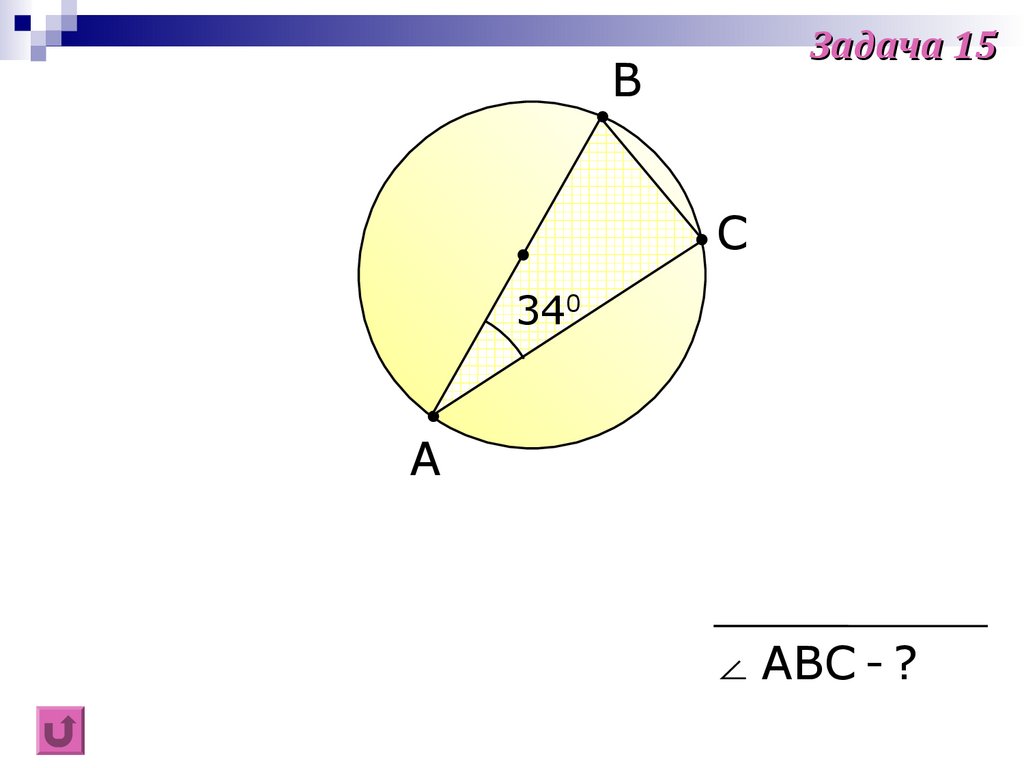
Задача 15B
C
340
A
∠ ABC - ?
30.
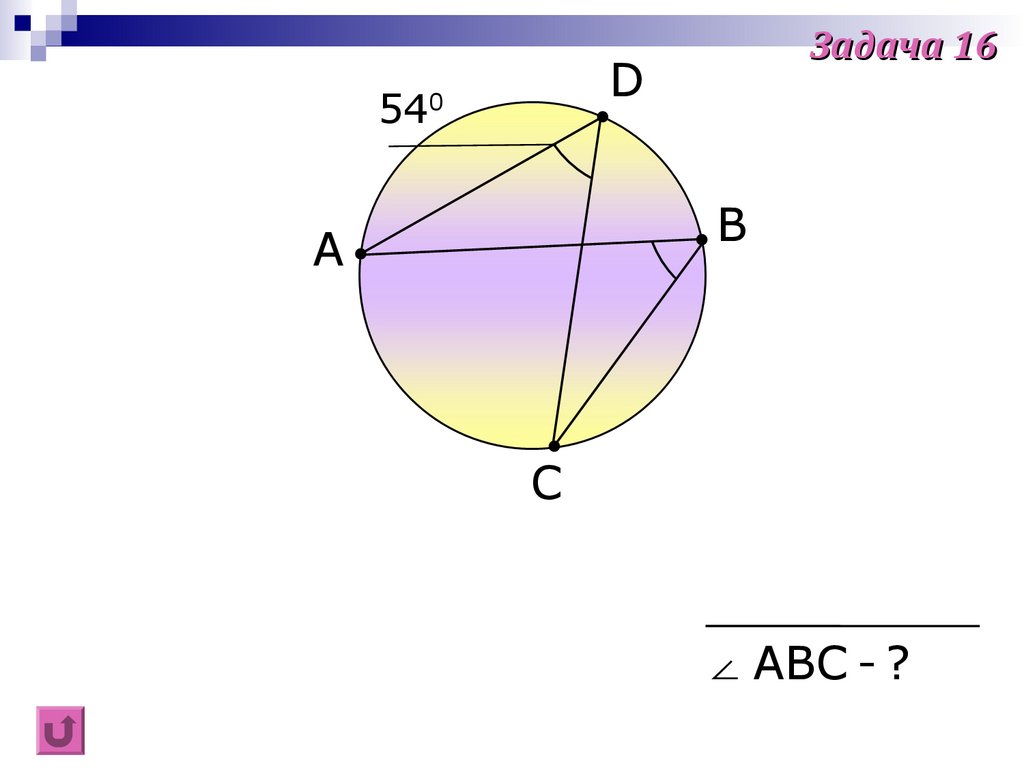
Задача 16D
54
0
B
A
C
∠ ABC - ?
31.
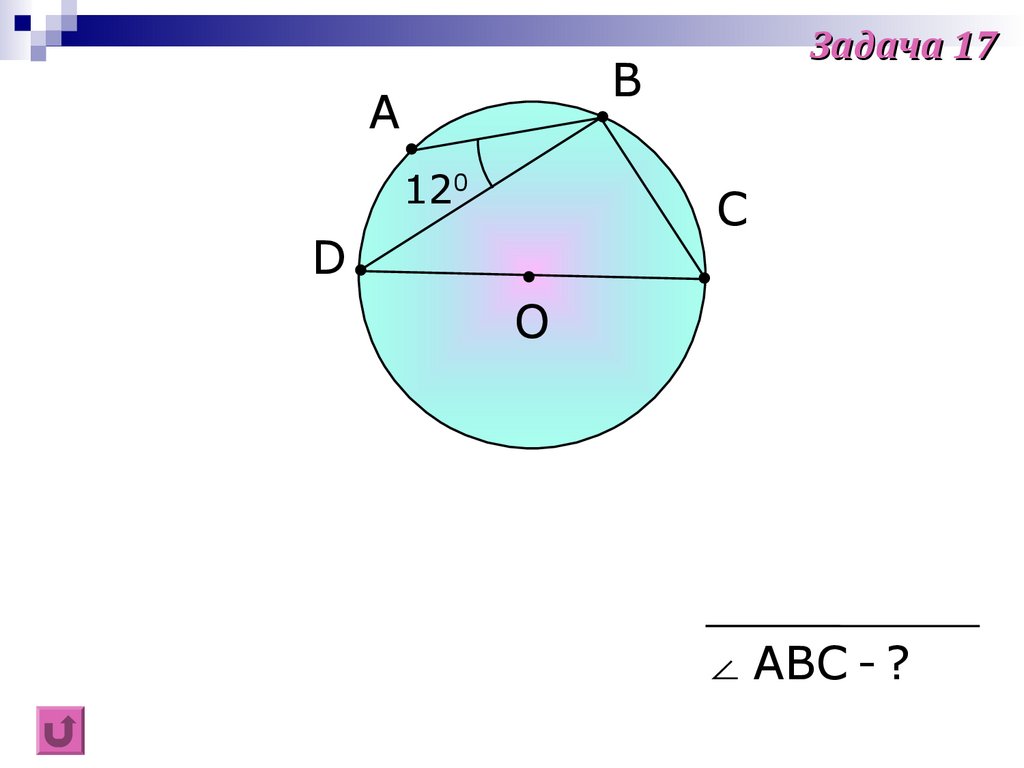
Задача 17B
A
120
C
D
O
∠ ABC - ?
32.
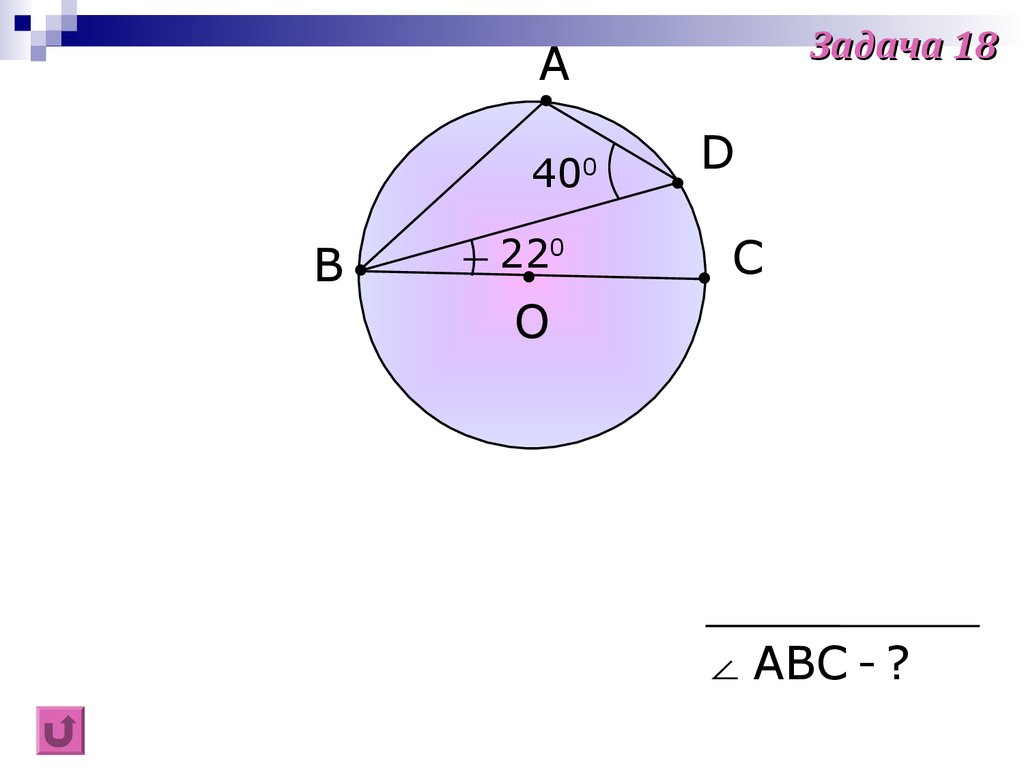
Задача 18A
400
B
220
D
C
O
∠ ABC - ?
33.
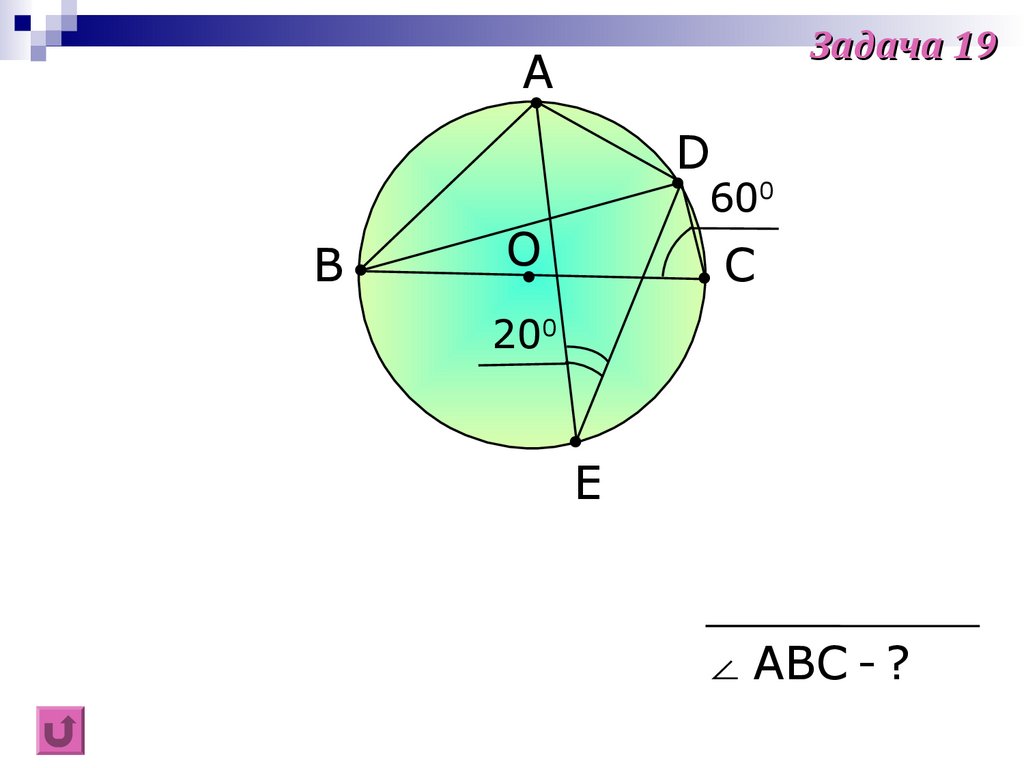
Задача 19A
D
B
600
O
C
200
E
∠ ABC - ?
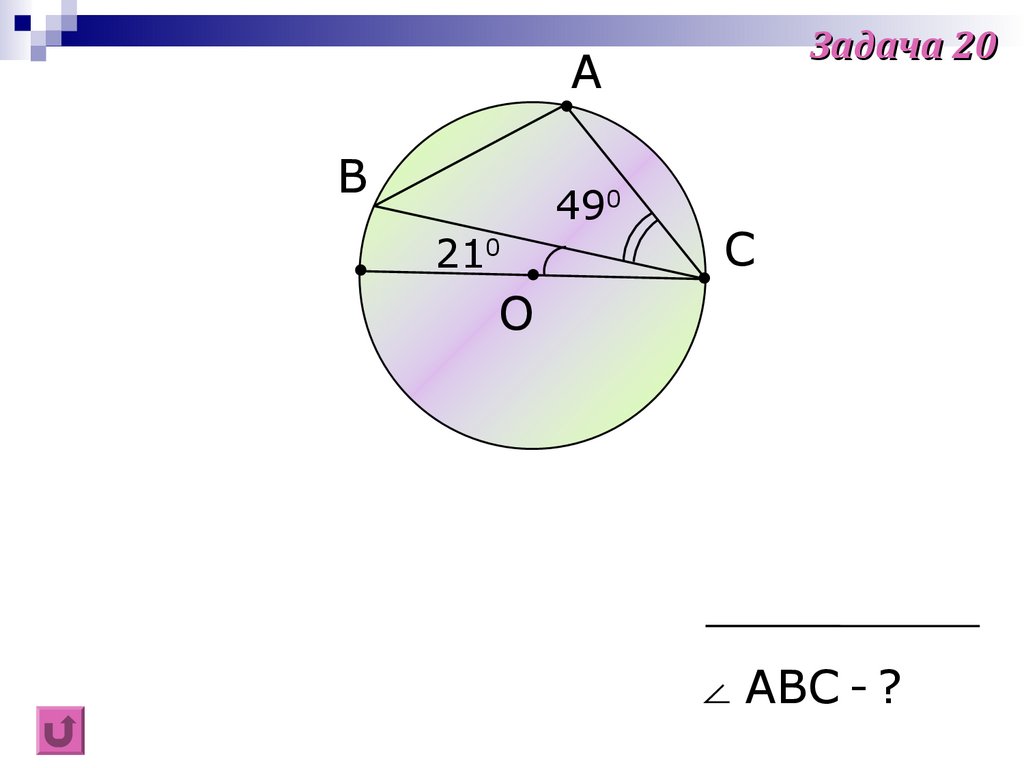
34.
Задача 20A
B
490
210
C
O
∠ ABC - ?
35.
Задача 21D
C
A
320 490
O
B
∠ ABC - ?
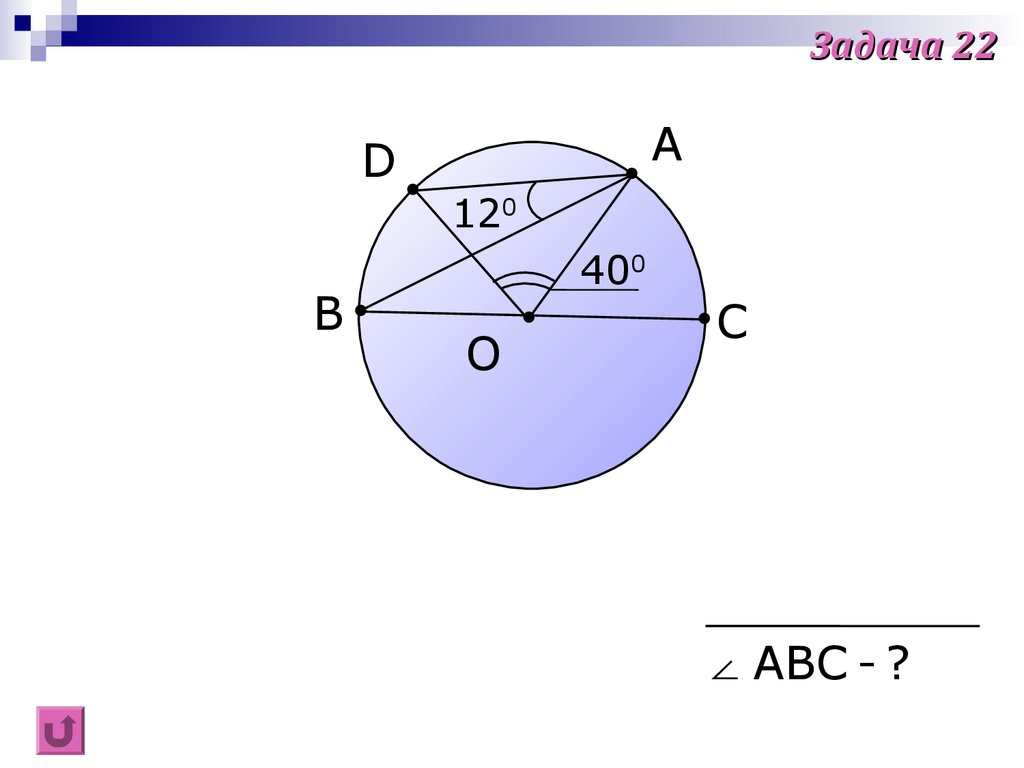
36.
Задача 22A
D
120
B
400
O
C
∠ ABC - ?
37.
Задача 23A
D
180
B
32
0
O
C
∠ ABC - ?
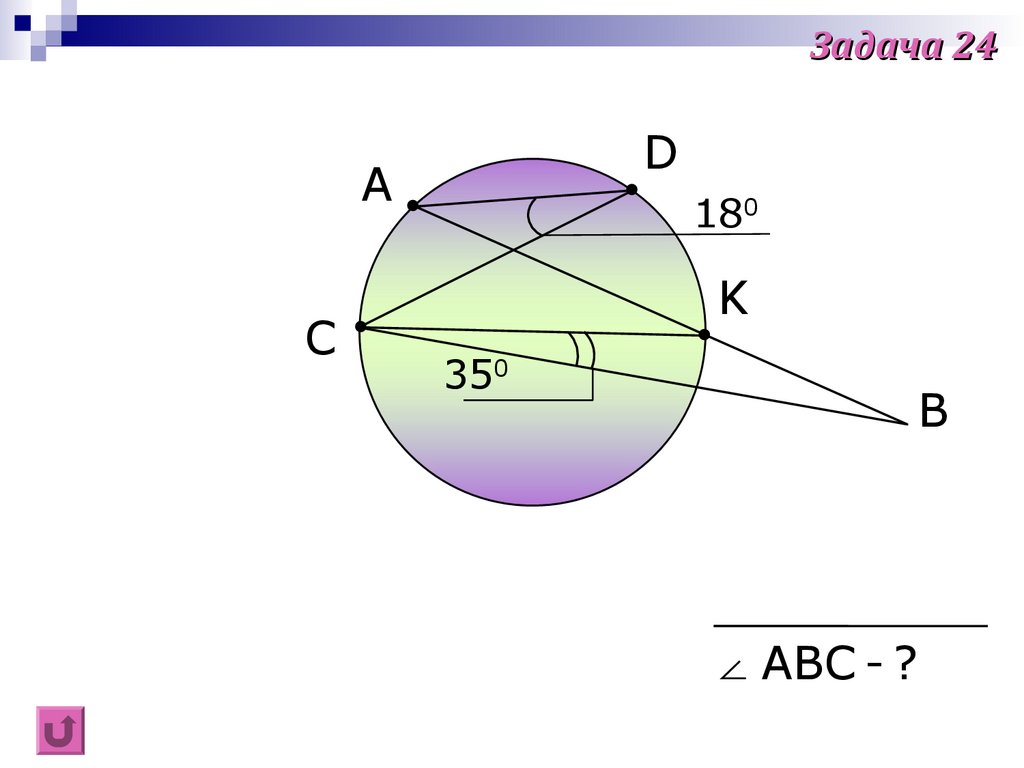
38.
Задача 24D
A
C
180
K
350
B
∠ ABC - ?
39.
Задача 25B
A
D
450
C
890
F
∠ ABC - ?
40.
Задача 26A
B
280
D
C
1000
F
∪BC - ?
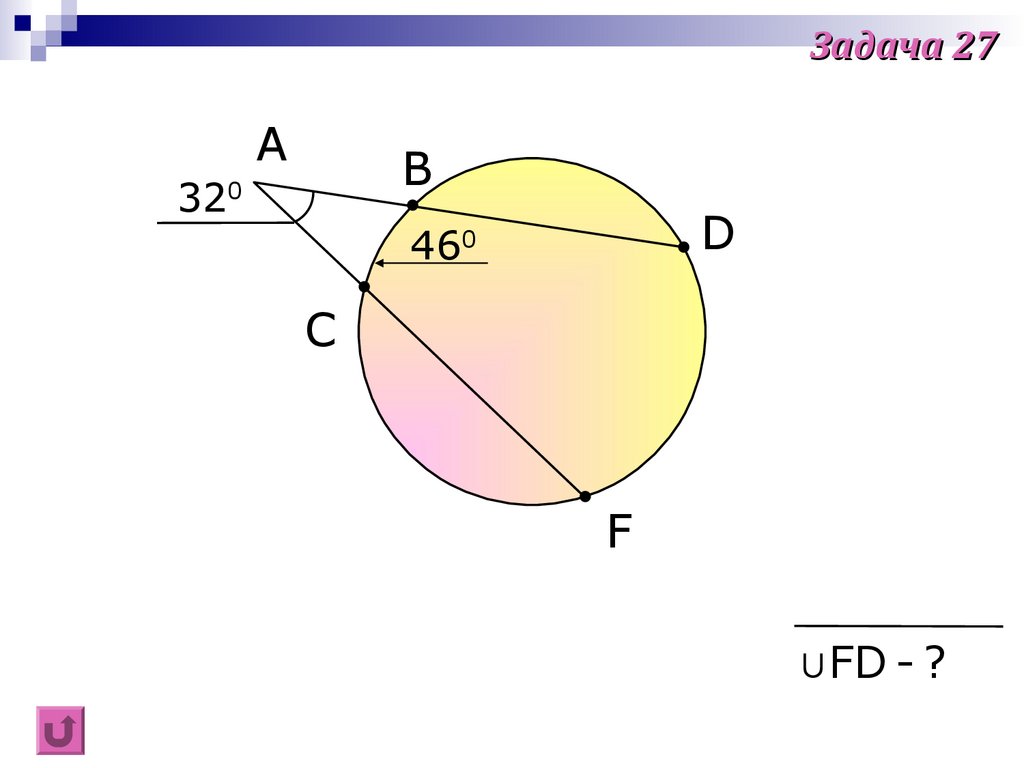
41.
Задача 27A
32
B
0
D
460
C
F
∪FD - ?
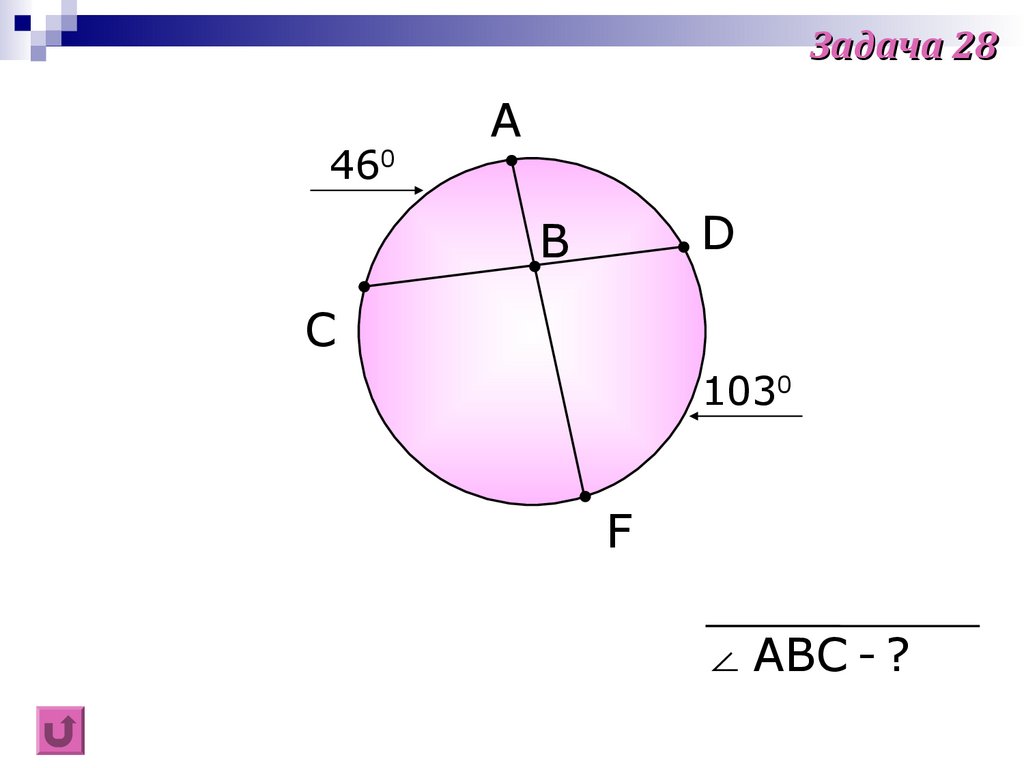
42.
Задача 28460
A
D
B
C
1030
F
∠ ABC - ?
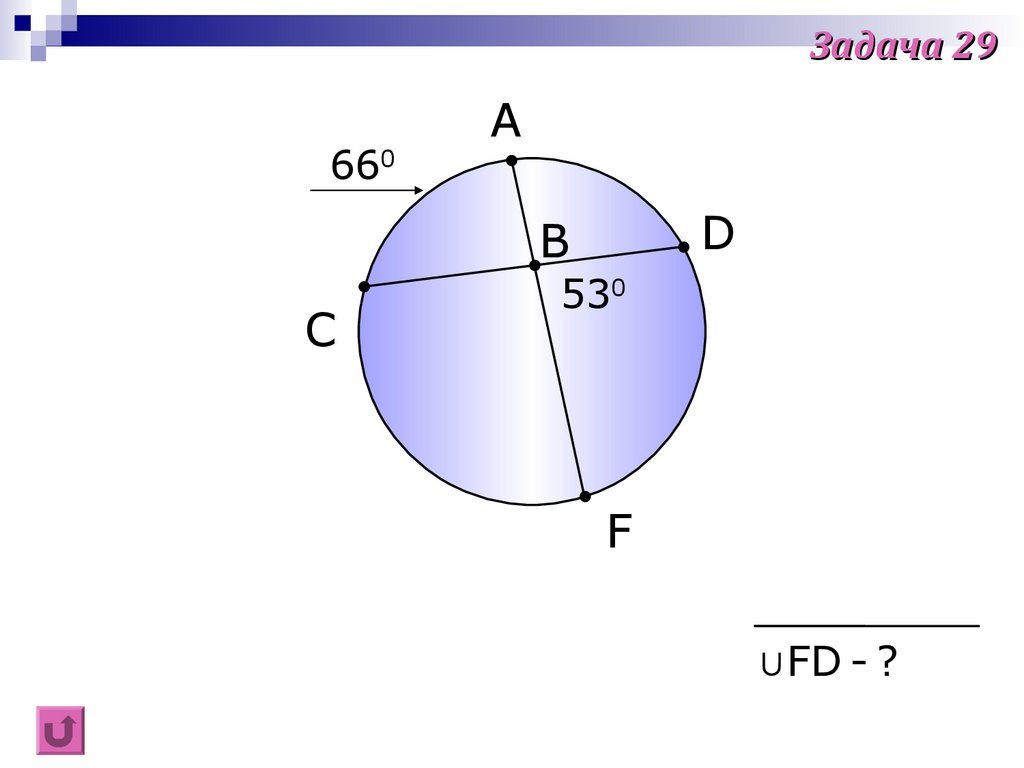
43.
Задача 29660
A
D
B
C
530
F
∪FD - ?
44.
Задача 30B
A
D
330
C
500
F
∠ ABC - ?
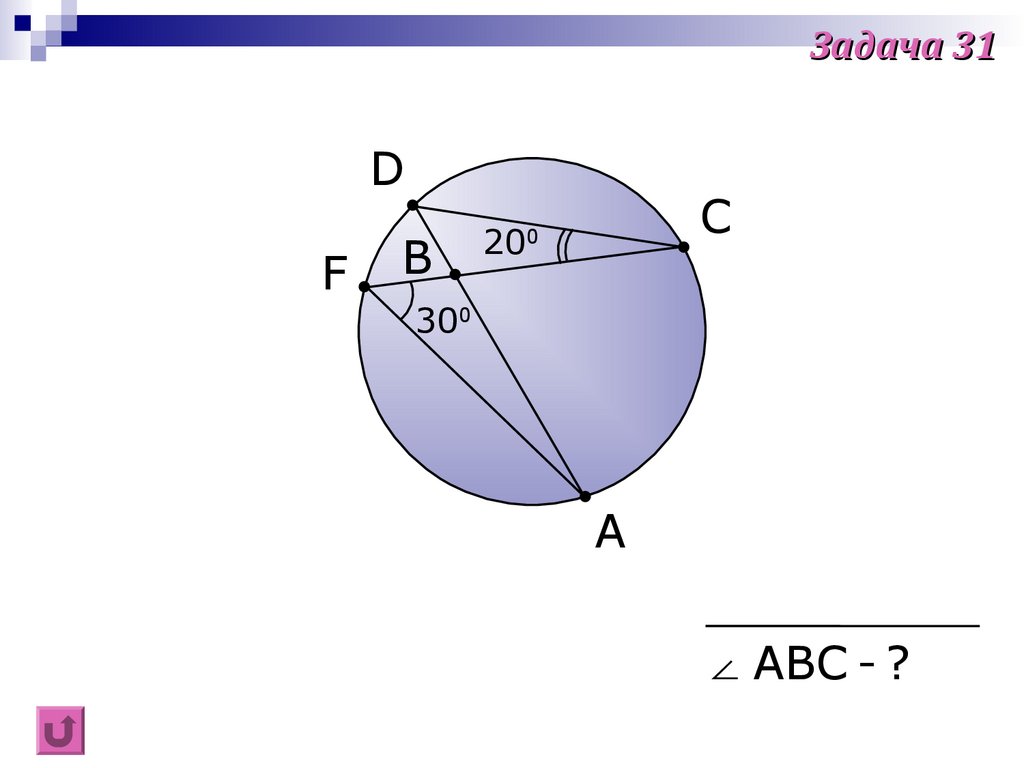
45.
Задача 31D
F
B
C
20
0
300
A
∠ ABC - ?
46. Прототип в6
Вписанные и описанные углы47. Прототип задания B6 (№ 27884)
Угол ACO равен 240. Его сторона CA касается окружности.Найдите градусную величину большей дуги AD окружности,
заключенной внутри этого угла. Ответ дайте в градусах.
∆АСО –прямоугольный. ∟С = 240 => ∟АОС = 660
Центральный угол измеряется дугой, на
которую опирается. Следовательно меньшая
дуга АВ = ∟АОС = 660
Развернутый угол DОB = 1800
∟DОA = ∟DOB - ∟AOB = 1800 - 660
∟DОA = 1140
∟DОA измеряется дугой АD, на которую опирается
Большая дуга АD окружности, заключенная
внутри ∟АСО равна 1140
27.01.22
Ответ 114
47
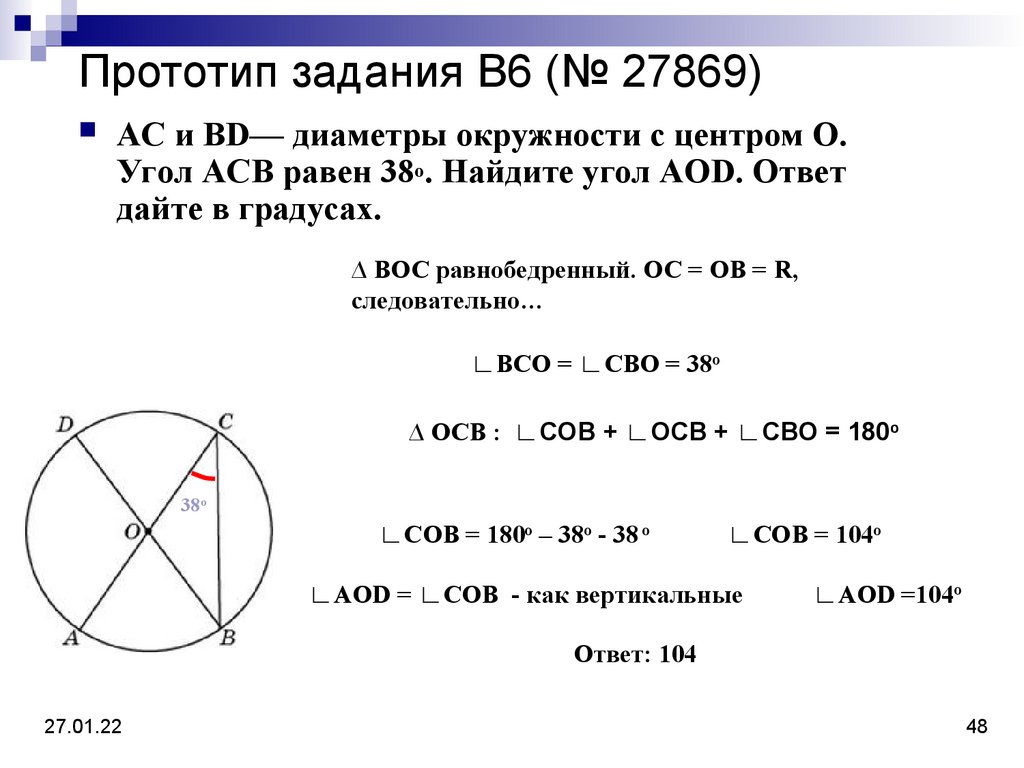
48. Прототип задания B6 (№ 27869)
АС и BD— диаметры окружности с центром О.Угол АСВ равен 38о. Найдите угол AOD. Ответ
дайте в градусах.
∆ ВОС равнобедренный. ОС = ОВ = R,
следовательно…
∟ВСО = ∟СВО = 38о
∆ ОСВ : ∟СОВ + ∟ОСВ + ∟СВО = 180о
38о
∟СОВ = 180о – 38о - 38 о
∟СОВ = 104о
∟AOD = ∟COB - как вертикальные
∟AOD =104о
Ответ: 104
27.01.22
48
49. Прототип задания B6 (№ 27878)
Угол между хордой AB и касательной BC к окружности равен32о. Найдите величину меньшей дуги, стягиваемой хордой AB.
Ответ дайте в градусах.
Угол, составленный касательной и хордой, измеряется
половиной дуги заключенной внутри него
Следовательно: Искомая меньшая дуга,
стягиваемой хордой АВ равна 32о · 2 = 64о
32о
Ответ 64
27.01.22
49
50. Прототип задания B6 (№ 27863)
Центральный угол на 36о больше острого вписанногоугла, опирающегося на ту же дугу окружности.
Найдите вписанный угол. Ответ дайте в градусах.
Вписанный угол АСВ составляет половину
центрального АОВ, опирающегося на туже дугу АВ
Пусть ∟АСВ = х
х
Тогда ∟АОВ = х + 36о
Так как ∟АОВ = 2∟АСВ, то
х + 36о = 2х
х = 36о
Ответ: 36
27.01.22
50
51. Прототип задания B6 (№ 27857)
Чему равен острый вписанный угол, опирающийся нахорду, равную радиусу окружности? Ответ дайте в
градусах.
По условию задачи АС = R , Следовательно АС = АО = СО
∆ АОС равносторонний => ∟АОС = 60о
В
Центральный угол АОС измеряется дугой АС, на
которую опирается.
Вписанный угол АВС составляет половину
центрального АОС, опирающегося на туже дугу АС
О
∟АВС = ½∟АОС
А
27.01.22
С
∟АВС = 60о : 2 = 30о
Ответ: 30
51
52. Задание B6 (№ 51031)
Найдите хорду, на которую опирается угол 30о ,вписанный в окружность радиуса 28.
Вписанный угол АВС составляет половину центрального
АОС, опирающегося на туже дугу АС
Дуга АС =2·30о = 60о
В
О
R
А
27.01.22
30о
Хорда АС = R = 28
R
R
∟АОС = 60о. Следовательно ∆АОС равносторонний
Ответ: 28
С
52
53.
Найдите угол ВАСДугу ВАС
Дугу ВС
Угол ВОС опирающийся на
дугу ВС





















 Математика
Математика








