Надежность в технике (основные понятия). Отказы и их причины. Статистический анализ

1.

Кафедра
«ЛОКОМОТИВЫ»
ОСНОВЫ ТЕОРИИ НАДЕЖНОСТИ
КУРС ЛЕКЦИЙ
Л. А. Сосновский
В. В. Комиссаров
Е. С. Таранова
Литература: Надежность. Риск. Качество / Л. А. Сосновский [и др.] ; науч.
ред. Л. А. Сосновский. – Гомель : БелГУТ, 2012. – 358 с.
Гомель ● 2019

2.

ЛИТЕРАТУРА
2
Основная:
1. Сосновский, Л.А. Элементы теории вероятностей, математической статистики и теории
надёжности / Л.А. Сосновский. – Гомель; БелГУТ, 1994. – 146 с. (в НТБ БелГУТа).
2. Шевченко Д.Н. Основы теории надежности : учеб.-методич. пособие для студ. техн. спец./
Д.Н. Шевченко; под ред. Л.А. Сосновского. – Гомель: БелГУТ, 2010. – 250 с. (в НТБ БелГУТа)
3. Богданович А.В. Оценка основных показателей надежности и риска невосстанавливаемых
изделий / А.В. Богданович, О.М. Еловой, Л.А. Сосновский. – Гомель : БелГУТ, 1995 г. – 95 с.
(в НТБ БелГУТа)
Дополнительная:
1. Надежность. Риск. Качество / Л. А. Сосновский [и др.] ; науч. ред. Л. А. Сосновский. – Гомель : БелГУТ, 2012. –
358 с.
2. Сосновский, Л.А. Вероятностные методы расчета на прочность при линейном и сложном напряженных
состояниях в 2-х частях: Метод. указания по изучению курса «Сопротивление материалов»/ Л.А. Сосновский. –
Гомель: БелИИЖТ, 1984. – 74с. (в НТБ БелГУТа).
3. Сосновский, Л.А. L-риск (механотермодинамика необратимых повреждений) / Л.А. Сосновский. – Гомель:
БелГУТ, 2004. – 317 с.
4. Сосновский, Л.А. Комплексная оценка надежности силовых систем по критериям сопротивления усталости и
износостойкости (основы трибофатики): Метод. указания по изучению курса «Надежность транспортных
систем, машин и сооружений» для студентов транспортных вузов / Л.А. Сосновский. – Гомель: БелИИЖТ, 1988.
–56 с. (в НТБ БелГУТа ).
5. Богданович, А.В. Оценка надежности простого коленчатого вала. Надежность по критериям трибофатики:
Пособие по курсу «Основы теории надежности» / А.В. Богданович, О.М. Еловой, Л.А. Сосновский. – Гомель:
БелГУТ, 2002. – Ч.2.–30 с. (в методическом кабинете кафедры – 5 экз.).
6. Сосновский, Л.А. Показатель безопасности и оперативная характеристика риска / Л.А. Сосновский. – Гомель,
БелИИЖТ, 1991. (в НТБ БелГУТа).

3.

ПЛАН ЛЕКЦИЙ
Лекция 1. Надежность в технике. Основные понятия
Отказы и их причины. Статистический анализ
Лекция 2. Концепция риска. Оценка безопасности
3

4.

НАДЕЖНОСТЬ В ТЕХНИКЕ
(основные понятия).
ОТКАЗЫ И ИХ ПРИЧИНЫ.
СТАТИСТИЧЕСКИЙ АНАЛИЗ

5.

ОСНОВНЫЕ ПОНЯТИЯ
5
Надежность – свойство объекта сохранять во времени и в
установленных
пределах
значения
всех
параметров,
характеризующих способность выполнять требуемые функции в
заданных режимах и условиях применения, технического
обслуживания, ремонтов, хранения и транспортирования
Объект – техническое изделие определенного целевого
назначения, рассматриваемое в периоды проектирования,
производства, испытаний и эксплуатации.
Объектами могут быть различные системы и их элементы.
Система – совокупность совместно действующих элементов,
предназначенная для самостоятельного выполнения заданных
функций.
Элемент – простейшая составная часть изделия, в задачах
надежности может состоять из многих деталей.

6.

СОСТОЯНИЯ ОБЪЕКТОВ
Понятие
Исправное
состояние
6
Определение
Состояние объекта, при котором он соответствует всем требованиям
нормативно-технической
и
(или)
конструкторской
(проектной)
документации
Неисправное
Состояние объекта, при котором он не соответствует хотя бы одному из
состояние
требований нормативно-технической и (или) конструкторской (проектной)
документации
Работоспособное
Состояние объекта, при котором значения всех параметров, характеризующих
состояние
способность выполнять заданные функции, соответствуют требованиям
нормативно-технической
и
(или)
конструкторской
(проектной)
документации
Неработоспособное Состояние объекта, при котором значение хотя бы одного параметра,
состояние
характеризующего способность выполнять заданные функции, не
соответствует
требованиям
нормативно-технической
и
(или)
конструкторской (проектной) документации
Предельное
Состояние объекта, при котором его дальнейшее применение по назначению
состояние
недопустимо или нецелесообразно, либо восстановление его исправного или
работоспособного состояния невозможно или нецелесообразно
Критерий
Признак или совокупность признаков предельного состояния объекта,
предельного
установленные
нормативно-технической
и
(или)
конструкторской
состояния
(проектной) документацией

7.

ВЗАИМОСВЯЗЬ ОСНОВНЫХ СОСТОЯНИЙ
ОБЪЕКТА
Исправное состояние
3
1 - Повреждение
2 – Отказ
3 – Переход объекта
в предельное
состояние
4 – Восстановление
5 – Ремонт
Неисправное состояние
2
1
Работоспособное состояние
Неработоспособное состояние
Предельное состояние
4
5
Списание
ВОПРОСЫ:
1. Может ли быть объект исправным, но неработоспособным?
2. Может ли быть объект работоспособным, но неисправным?
7

8.

СОБЫТИЯ. СВОЙСТВА ОБЪЕКТОВ
Понятие
8
Определение
Повреждение
Событие, заключающееся в нарушении исправного состояния объекта
при сохранении работоспособного состояния
Отказ
Событие, заключающееся в нарушении работоспособного состояния
объекта
Надежность – наука об отказах
Безотказность
Долговечность
Ремонтопригодность
Сохраняемость
Показатели надежности
Свойство объекта непрерывно сохранять работоспособность (т. е. не
иметь отказов) в течение некоторого времени или некоторой наработки
Свойство объекта сохранять работоспособное состояние до наступления
предельного состояния при установленной системе технического
обслуживания
Свойство
объекта,
заключающееся
в
приспособленности
к
предупреждению и обнаружению причин возникновения отказов,
повреждений и поддержанию и восстановлению работоспособного
состояния путем проведения технического обслуживания и ремонта
Свойство объекта сохранять значение показателей безотказности,
долговечности и ремонтопригодности в течение и после хранения и
(или) транспортирования
Количественная характеристика одного или нескольких свойств надежности

9.

ИНТЕГРАЛЬНЫЕ ПОКАЗАТЕЛИ
НАДЕЖНОСТИ
Понятие
9
Определение
Наработка
Наработка до
отказа
Технический
ресурс
Продолжительность или объем работы объекта
Наработка объекта от начала его эксплуатации до
возникновения первого отказа
Наработка объекта от начала его эксплуатации или ее
возобновления после ремонта определенного вида до
перехода в предельное состояние
Срок службы Календарная продолжительность от начала эксплуатации
объекта
или
ее
возобновления
после
ремонта
определенного вида до перехода в предельное состояние
ВОПРОС:
Что больше – технический ресурс или срок службы?

10.

ПОКАЗАТЕЛИ БЕЗОТКАЗНОСТИ
Понятие
Вероятность
безотказной
работы
Средняя наработка
до отказа
Гамма-процентная
наработка до отказа
Средняя наработка
на отказ
Интенсивность
отказов
Параметр
отказов
10
Определение
Вероятность того, что в пределах заданной наработки отказ объекта не
возникает
Математическое ожидание наработки объекта до первого отказа
Наработка, в течение которой отказ объекта не возникает, с
вероятностью γ, выраженной в процентах
Отношение наработки восстанавливаемого объекта к математическому
ожиданию числа его отказов в течение этой наработки
Условная
плотность
вероятности
возникновения
отказа
невосстанавливаемого объекта, определяемая для рассматриваемого
момента времени при условии, что до того момента отказ не возник
потока Показатель
надежности
восстанавливаемых
изделий,
равный
отношению среднего числа отказов восстанавливаемого объекта за
произвольную малую его наработку к значению этой наработки
(соответствует интенсивности отказов для неремонтируемых изделий,
но включает повторные отказы)

11.

ПОКАЗАТЕЛИ ДОЛГОВЕЧНОСТИ
Понятие
11
Определение
Средний ресурс Математическое ожидание ресурса
Гаммапроцентный
ресурс
Назначенный
ресурс
Средний срок
службы
Гаммапроцентный
срок службы
Назначенный
срок службы
Наработка, в течение которой объект не достигнет
предельного состояния, с заданной вероятностью γ,
выраженной в процентах
Суммарная наработка объекта, при достижении которой
применение по назначению должно быть прекращено
Математическое ожидание срока службы
Календарная
продолжительность
от
начала
эксплуатации объекта, в течение которой он не достиг
предельного состояния с заданной вероятностью γ,
выраженной в процентах
Календарная продолжительность эксплуатации объекта,
при достижении которой применение по назначению
должно быть прекращено

12.

ПОКАЗАТЕЛИ РЕМОНТОПРИГОДНОСТИ
И СОХРАНЯЕМОСТИ
Понятие
12
Определение
ПОКАЗАТЕЛИ РЕМОНТОПРИГОДНОСТИ
Вероятность
восстановления
работоспособного
состояния
Среднее
время
восстановления
работоспособного
состояния
Понятие
Вероятность
того,
что
работоспособного состояния
заданного
Математическое
ожидание
работоспособного состояния
время
объекта
времени
восстановления
не превысит
восстановления
Определение
ПОКАЗАТЕЛИ СОХРАНЯЕМОСТИ
Средний
срок Математическое ожидание срока сохраняемости
сохраняемости
Гамма-процентный Срок сохраняемости, достигаемый объектом с заданной
срок сохраняемости вероятностью γ, выраженной в процентах

13.

КОМПЛЕКСНЫЕ ПОКАЗАТЕЛИ
НАДЕЖНОСТИ
13
Понятие
Коэффициент
Готовности
Определение
Вероятность того, что объект окажется в работоспособном состоянии в
произвольный момент времени, кроме планируемых периодов, в течение
которых применение объекта по назначению не предусматривается
Коэффициент
оперативной
Готовности
Вероятность того, что объект окажется в работоспособном состоянии в
произвольный момент времени, кроме планируемых периодов, в течение
которых применение объекта по назначению не предусматривается, и,
начиная с этого момента, будет работать безотказно в течение заданного
интервала времени
Отношение математического ожидания интервалов времени пребывания
объекта в работоспособном состоянии за некоторый период эксплуатации к
сумме математических ожиданий интервалов времени пребывания объекта
в работоспособном состоянии, простоев, обусловленный техническим
обслуживанием, и ремонтов за тот же период эксплуатации
Коэффициент
технического
использования
Коэффициент
планируемого
применения
Коэффициент
сохранения
эффективности
Доля периода эксплуатации, в течение которой объект не должен
находиться в плановом техническом обслуживании и ремонте
Отношение значения показателя эффективности за определенную
продолжительность эксплуатации к номинальному значению этого
показателя, вычисленного при условии, что отказы объекта в течении того
же периода эксплуатации не возникают

14.

ОТКАЗЫ И ИХ ПРИЧИНЫ.
СТАТИСТИЧЕСКИЙ АНАЛИЗ

15.

КЛАССИФИКАЦИЯ ОТКАЗОВ
Признак
классификации
по характеру
развития
и проявления
по последствиям
Вид отказа
поломки от перегрузки, заедания; сгорание
предохранителя; поломка рельса
б) постепенные
в) постепенные по
развитию и внезапные
по появлению
а) легкие
б) средние
износ, старение, коррозия, залипание
усталостное разрушение, перегорание ламп,
короткие
замыкания
из-за
старения
изоляции
легко устранимые
не вызывают отказ других узлов
а) полный отказ
б) частичный
а) приработочные
по времени
возникновения
Примеры
а) внезапные
в) тяжелые
по возможности
дальнейшего
использования
1
5
тяжелые вторичные разрушения, в том числе
и с человеческими жертвами
исключает возможность работы изделия до
устранения отказа
изделие может частично использоваться,
например, с неполной мощностью, или на
пониженных оборотах
обусловленные, например, деформациями
при изготовлении
б) при нормальной
обусловленные,
(штатной)
повреждений
эксплуатации
например,
накоплением

16.

КЛАССИФИКАЦИЯ ОТКАЗОВ
Признак
классификации
Вид отказа
а) конструкционные
по причине
возникновения
б) производственные
1
6
Примеры
обусловленные
ошибками
при
конструировании
условия изготовления, сварки, технического
обслуживания
в) эксплуатационные
обусловлены нарушением установленных
правил эксплуатации и текущего содержания
а) случайные
непредусмотренные перегрузки, дефекты
материала и погрешности изготовления, не
обнаруженные
контролем;
ошибки
обслуживающего
персонала
или
сбои
системы управления
б) систематические
закономерные
явления,
вызывающие
постепенное
накопление
повреждений:
влияние среды, времени, температуры,
облучения, коррозия, старение, нагрузки и
работа трения, усталость, ползучесть, износ,
засорения, залипания, утечки
по
закономерностям
возникновения

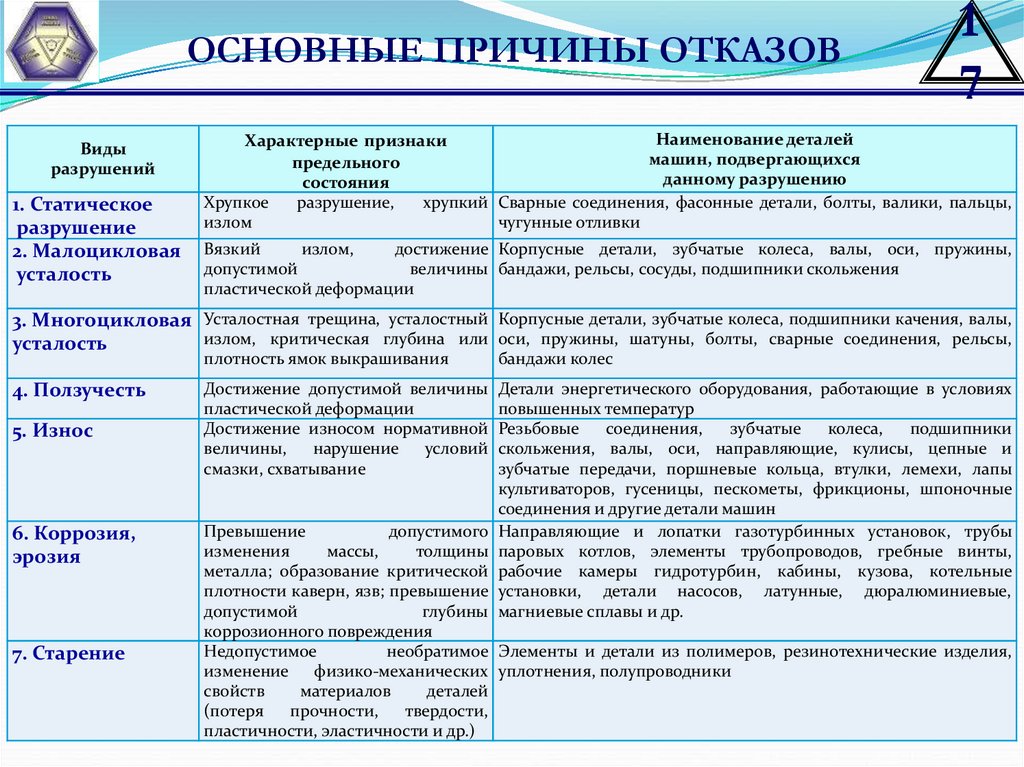
17.

ОСНОВНЫЕ ПРИЧИНЫ ОТКАЗОВ
Виды
разрушений
1. Статическое
разрушение
2. Малоцикловая
усталость
1
7
Наименование деталей
Характерные признаки
машин, подвергающихся
предельного
данному разрушению
состояния
Хрупкое
разрушение,
хрупкий Сварные соединения, фасонные детали, болты, валики, пальцы,
излом
чугунные отливки
Вязкий
излом,
достижение Корпусные детали, зубчатые колеса, валы, оси, пружины,
допустимой
величины бандажи, рельсы, сосуды, подшипники скольжения
пластической деформации
3. Многоцикловая Усталостная трещина, усталостный Корпусные детали, зубчатые колеса, подшипники качения, валы,
излом, критическая глубина или оси, пружины, шатуны, болты, сварные соединения, рельсы,
усталость
4. Ползучесть
5. Износ
6. Коррозия,
эрозия
7. Старение
плотность ямок выкрашивания
бандажи колес
Достижение допустимой величины
пластической деформации
Достижение износом нормативной
величины,
нарушение условий
смазки, схватывание
Детали энергетического оборудования, работающие в условиях
повышенных температур
Резьбовые
соединения,
зубчатые
колеса,
подшипники
скольжения, валы, оси, направляющие, кулисы, цепные и
зубчатые передачи, поршневые кольца, втулки, лемехи, лапы
культиваторов, гусеницы, пескометы, фрикционы, шпоночные
соединения и другие детали машин
Направляющие и лопатки газотурбинных установок, трубы
паровых котлов, элементы трубопроводов, гребные винты,
рабочие камеры гидротурбин, кабины, кузова, котельные
установки, детали насосов, латунные, дюралюминиевые,
магниевые сплавы и др.
Превышение
допустимого
изменения
массы,
толщины
металла; образование критической
плотности каверн, язв; превышение
допустимой
глубины
коррозионного повреждения
Недопустимое
необратимое Элементы и детали из полимеров, резинотехнические изделия,
изменение физико-механических уплотнения, полупроводники
свойств
материалов
деталей
(потеря
прочности,
твердости,
пластичности, эластичности и др.)

18.

КЛАССИФИКАЦИЯ ОБЪЕКТОВ ПО
ПОСЛЕДСТВИЯМ ОТКАЗА
Отказ
Допустимая
вероятность
безотказной
работы
Последствия
отказа
Авария
Тяжелые
(катастрофические)
Катастрофа
Q( t ) 1
Невыполнение
ответственного
задания
Повышенные
простои в
ремонте
Средние
(экономический
ущерб)
Легкие
(затраты на ремонт в
пределах нормы)
Работа на
пониженных
режимах
Работа с
ухудшенными
параметрами
1
8
Тип изделий
Летательные аппараты
Подъемно-транспортные
машины
Военная техника
Машины химического
производства
Медицинское
оборудование
Значительный
ущерб
Q( t ) 0,99
Незначительный
ущерб
Без
последствий
Вероятность отказов
Q( t ) 0,9
Q( t ) 0,9
P( t ) 1 Q( t )
Технологическое
оборудование
Сельскохозяйственные
Бытовые
Отдельные узлы и элементы
машин

19.

СТАТИСТИЧЕСКИЙ АНАЛИЗ:
СОДЕРЖАНИЕ
1.
2.
3.
4.
5.
1
9
Планирование эксперимента, в частности, установление метода
получения выборок и определения их требуемого объема
Оценка выборочных параметров распределения и числовых
характеристик случайной величины
Выбор математико-статистической модели для описания рассеяния
результатов испытания. Проверка гипотез
Построение предварительных интервалов для оцениваемых параметров
Анализ статистических связей
• ковариация;
• коэффициент корреляции Пирсона;
• ранговый коэффициент корреляции Спирмена;
• регрессионный анализ;
• дисперсионный анализ;
• проверка научных гипотез

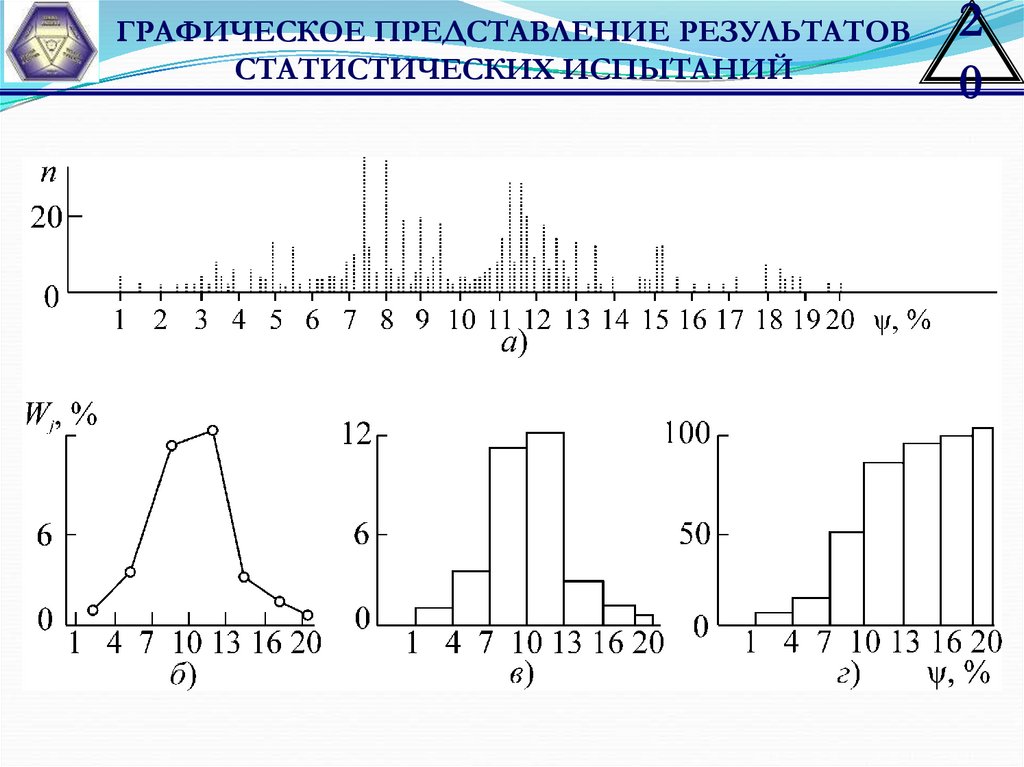
20.

ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ РЕЗУЛЬТАТОВ
СТАТИСТИЧЕСКИХ ИСПЫТАНИЙ
2
0

21.

2
1
ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ
СЛУЧАЙНОЙ ВЕЛИЧИНЫ
Формулы
Наименование
n 50
Среднее значение
Дисперсия
Среднее квадратическое
отклонение
Коэффициент вариации
Размах распределения
Начальные моменты
распределения
Центральные моменты
Показатель
асимметрии
Показатель эксцесса
x
D x
n 50
n
1
xi
n i 1
x
1 n
xi xi 2
n 1 i 1
D x
1 m
x jn j
n j 1
1 m
nj xj xj
n 1 j 1
S x D x
S x k D x
vx S x x
vx S x x
Rx xn x1
Rx xmax xmin
1 m 3
1 m 4
h3 x j n j , h4 x j n j
n j 1
n j 1
h1 x ,
h2
1 m 2
xjnj,
n j 1
m4 h4 4h3h1 6h2 h12 3h14
m3 h3 3h2 h1 2h13 ,
ak m3 S x3
Ek
m4
3
S x4
2

22.

ОСНОВНЫЕ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ
Наименование
распределения
Плотность распределения
Параметры
, S x 0
Нормальное
2
1
1 x
,
p x
exp
2 S x
S x 2
x
Усеченное
нормальное
p x
2
1 x
exp
,
2 S x
2 1 C
1
Sx
, S x 0
a
C f x dx
x a,
Логарифмически
нормальное
– среднее
значение и
среднее
квадратическое
отклонение
p ln x
1
S ln x
2
1 ln x
exp
,
2 S ln x
2
ln x,
S ln x 0
x
– параметр
масштаба; 0 –
параметр формы;
0
Вейбулла
p x
x C
x C
exp
,
x C
C 0
Гамма
Экспоненциальное
p x
h 1
x exp x ,
Г
x 0,
Г( ) – гамма-функция
p x exp x ,
x 0
0;
0
0
2
2

23.

НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
P x
1
2
x
e
x 2
2S 2
dx
1
2
x
S
e
u 2 / 2
x
du Ф
,
S
2
3

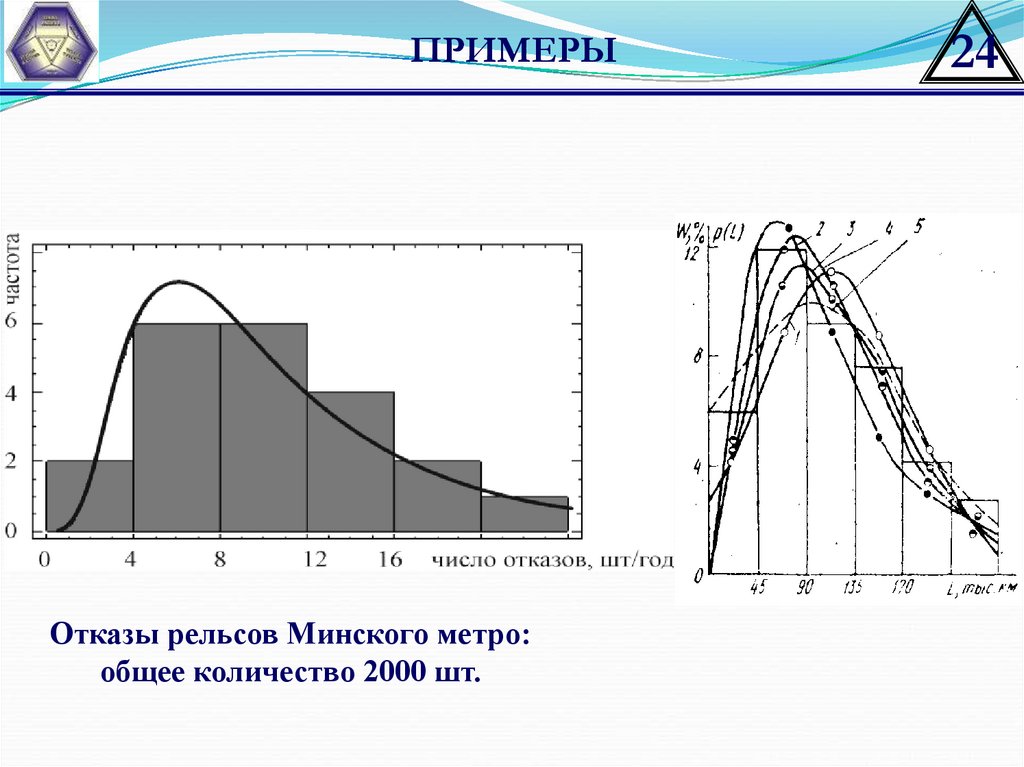
24.

ПРИМЕРЫ
Отказы рельсов Минского метро:
общее количество 2000 шт.
24

25.

ДОПОЛНЕНИЯ

26.

ОБЛАСТИ ПРИМЕНЕНИЯ И ОСОБЕННОСТИ
ТИПИЧНЫХ ОДНОМЕРНЫХ РАСРЕДЕЛЕНИЙ
Распределение
Применение
Нормальное
Основное
распределение
математической
распределение статистики. Многие применения обусловлены
центральной
предельной
теоремой
(распределение
среднего
n
независимых
случайных величин, распределенных по любому
закону или даже имеющих до n различных
распределений с конечными математическим
ожиданием и дисперсией, при n
приближается к нормальному). Вследствие этого
нормальное распределение является приемлемой
моделью для многих (но не для всех) физических
явлений. Многие методы статистического анализа основаны на допущении о нормальном
распределении.
Распределение
случайных
величин, появляющихся как результат небольшого воздействия многих независимых факторов.
Область
изменения
нормально
распределенной случайной величины (– x
+ )
Усеченное
Модель применима к выборке из нормальной
нормальное
совокупности, из которой первоначально были
распределение изъяты все элементы, меньшие некоторых
заданных предельных значений
26
Примеры
Примечание
Распределение пределов текучести,
прочности,
выносливости,
твердости;
размеров
изделия;
циклической долговечности при
относительно
высоких
напряжениях.
Распределение
инструментальных ошибок. Используется
для
генерирования
случайных чисел, распределенных
по нормальному закону
Имеются таблицы
интегральной
функции
распределения
и
нормированной
плотности
вероятностей
Распределение
логарифма Частный
случай
циклической
долговечности, нормального
предельных напряжений, если распределения
выборка
производится
с
отбрасыванием значений, меньших,
чем
требуется
нормативным
документом

27.

ОБЛАСТИ ПРИМЕНЕНИЯ И ОСОБЕННОСТИ
ТИПИЧНЫХ ОДНОМЕРНЫХ РАСРЕДЕЛЕНИЙ
Распределение
Применение
Логарифмическ Позволяет описать случайные величины, логарифм
и нормальное которых распределен по нормальному закону. Модель
распределение для процесса, появляющегося в результате большого
числа небольших мультипликативных ошибок.
Применимо, когда наблюдаемое значение случайной
величины составляет случайную долю ранее
наблюденного явления
Экспоненциаль Распределение времени между независимыми
ное
событиями,
появляющимися
с
постоянной
распределение интенсивностью. Распределение времени безотказной
работы при постоянной интенсивности отказов.
Вследствие этого широко применяется во многих (но
не во всех) задачах теории надежности
Распределение
Вейбулла
Гаммараспределение
Примеры
Распределение
циклической
долговечности,
распределение
времени
безотказной
работы
некоторых изделий
Распределение времени безотказной
работы сложных нерезервированных
систем и времени использования
некоторых компонентов, когда они, в
частности, подвергаются начальной
приработке,
а
профилактическое
обслуживание позволяет заменять
детали до полного износа
Общее распределение времени безотказной работы Распределение времени безотказной
при
разнообразных
интенсивностях
отказов. работы для ряда деталей, шариковых
Распределение
экстремальных
значений
для подшипников и др.
минимальных элементов, взятых из n значений,
имеющих распределение, ограниченное слева
Основное распределение математической статистики
для случайных величин, ограниченных с одной
стороны, например, 0 х . Описывает время,
необходимое для появления ровно , независимых
событий при условии появления событий с
постоянной интенсивностью . Часто используется в
теории надежности, теории массового обслуживания
Распределение времени безотказной
работы
системы
с
резервными
элементами; распределение времени
между повторными калибровками
прибора,
требующего
повторной
калибровки после пользования им
раз.
Распределение
времени
безотказной работы, если система
выходит из строя, когда в ней
произойдет независимых частичных
отказов,
имеющих
постоянную
интенсивность
27
Примечание
Частный
случай
распределения
Вейбулла,
гаммараспределения
Частными случаями
являются
экспоненциальное
распределение,
рэлеевское
распределение.
Имеются
таблицы
интегральной
функции
распределения
и
плотности
вероятностей
Имеются
таблицы
интегральной
функции
распределения.
Частными случаями
являются:
распределения
экспоненциальное,
хи-квадрат, Эрланга

28.

ОБЛАСТИ ПРИМЕНЕНИЯ И ОСОБЕННОСТИ
ТИПИЧНЫХ ОДНОМЕРНЫХ РАСРЕДЕЛЕНИЙ
Распределение
Применение
БетаОсновное распределение математической статистики
распределение для случайных величин, ограниченных с обеих сторон
(0 х 1), например, распределение доли
совокупности, заключенной между наименьшим и
наибольшим значениями выборки. Применяется во
многих областях при решении как теоретических, так
и практических задач
Примеры
Распределение доли совокупности,
заключенной между наименьшим и
наибольшим значениями выборки.
Распределение
суточного
производства
продукции
на
промышленном
предприятии.
Распределение времени до завершения
работы
Равномерное
распределение
Используется
для
случайных чисел
Рэлеевское
распределение
Распределение
Коши
Распределение
экстремальных
значений
Дает вероятность того, что наблюдение будет лежать
в определенном интервале, когда вероятность того,
что наблюдение принадлежит данному интервалу,
прямо пропорциональна его длине
Распределение радиальной ошибки, когда ошибки по
двум взаимно перпендикулярным осям взаимно
независимы и нормально распределены относительно
нуля с одинаковыми дисперсиями
Распределение
отношения
двух
независимых
нормированных нормальных случайных величин
28
Примечание
Имеются
таблицы
интегральной
функции
распределения.
Частными случаями
являются:
равномерное,
треугольное,
параболическое распределения
генерирования Частный случай бетараспределения
Задачи
прицеливания
при
бомбометании. Амплитуда огибающей
шума при использовании линейного
детектора
Распределение
отношения
нормированных отсчетов шума
Частный
случай
распределения
Вейбулла
Распределение
не
имеет
конечных
моментов
Распределение минимального или максимального Распределение предела прочности для Имеются
таблицы
значения в выборке, взятой из совокупности, некоторых материалов. Распределение интегральной
имеющей некоторое исходное распределение
силы порывов ветра, встречаемые функции
самолетами.
распределения
Модель для времени безотказной
работы цепи, состоящей из большого
числа последовательно соединенных
элементов,
при
условии,
что
длительности
их
работы
–
независимые случайные величины,
распределенные
по
нормальному
закону с одинаковыми параметрами

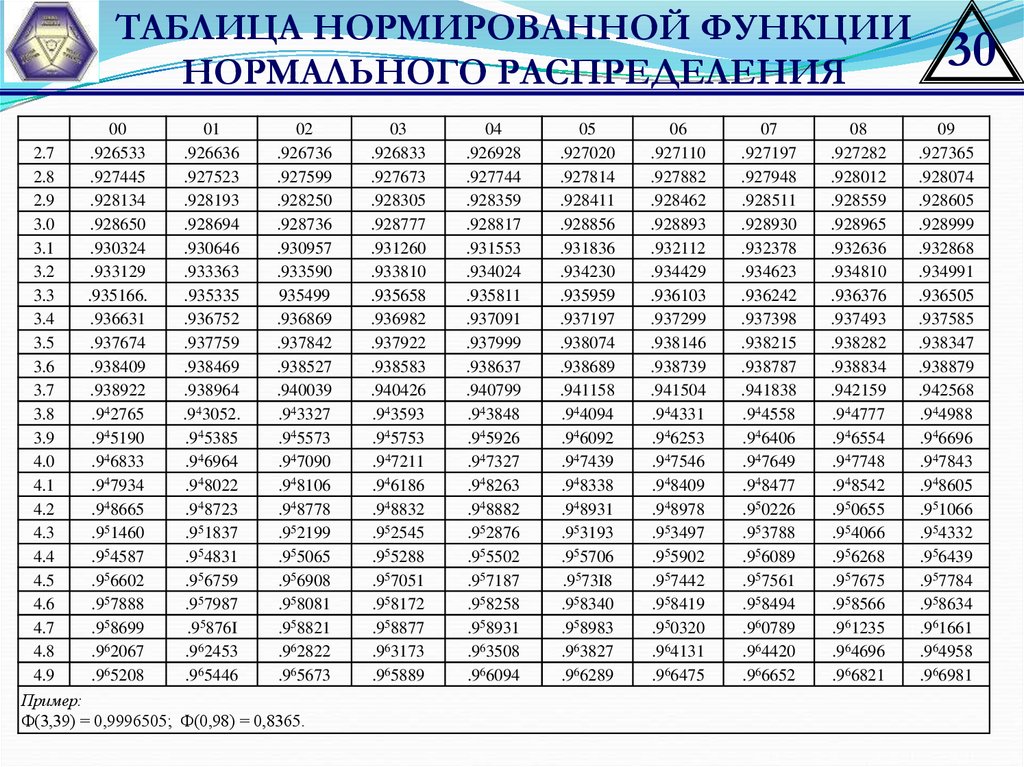
29.

ТАБЛИЦА НОРМИРОВАННОЙ ФУНКЦИИ
НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ
Ф u
.0
.1
.2
.3
.4
.5
.6
.7
.8
.9
1.0
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
2.0
2.1
2.2
2.3
2.4
2.5
2.6
00
.5000
.5398
.5793
.6179
.6554
.8915
.7257
.7560
.7881
.8159
.8413
.8643
.8849
.90320
.91924
.93319
.94520
.95543
.96407
.97128
.97725
.98214
.98610
.98928
.921802
.923790
.925339
01
.5040
.5438
.5832
.5217
.6591
.6950
.7291
.7611
.7910
.8186
.8438
.8665
.8869
.90490
.92073
.93448
.94630
.95637
.96485
.97193
.97778
.98257
.98645
.98956
.922024
.923963
.925473
02
.5080
.5478
.5871
.6255
.6628
.6985
.7324
.7642
.7939
.8212
.8461
.8686
.8888
.90658
.92220
.93574
.94738
.95728
.96562
.97257
.97831
.98300
.98679
.98983
.922240
.924132
.925604
03
.5120
.5517
.5910
.6293
.6664
.7019
.7357
.7673
.7967
.8238
.8485
.8708
.8907
.90824
.92364
.93699
.94845
.95818
.96638
.97320
.97882'
.98341
.98713
.920097
.922451
.924297
.925731
1
2
04
.5160
.5557
.5948
.6331
.6700
.7054
.7389
.7703
.7995
.8264
.8508
.8729
.8925
.90988
.92507
.93822
.94950
.95907
.96712
.97381
.97932
.98382
.98745
.920358
.922656
.924457
.925855
u
e
u 2 / 2
05
.5199
.5596
.5987
.6368
.6736
.7088
.7422
.7734
.8023
.8289
.8531
.8749
.8944
.91149
.92647
.93943
.95053
.95994
.96784
.97441
.97982
.98422
.98778
.920613
.922857
.924614
.925975
06
.5239
.5636
.6026
.6406
.6772
.7123
.7454
.7764
.8051
.8315
.8554
.8770
.8962
.91309
.92785
.94062
.95154
.96080
.96856
.97500
.98030
.98461
.98809
.920863
.923053
.924766
.926093
07
.5279
.5675
.6064
.6443
.6808
.7157
.7486
.7794
.8078
.8340
.8577
.8790
.8980
.91466
.92922
.94179
.95254
.96164
.96926
.97558
.98077
.98500
.98840
.921106
.923244
.924915
.926207
08
.5319
.5714
.6103
.6480
.6844
.7190
.7517
.7823
.8106
.8365
.8599
.8810
.8997
.91621
.93056
.94295
.95352
.96246
.96995
.97615
.98124
.98537
.98870
.921344
.923431
.925060
.926319
09
.5359
.5753
.6141
.6517
.6879
.7224
.7549
.7852
.8133
.8389
.8621
.8830
.90147
.91774
.93189
.94408
.95449
.96327
.97062
.97670
.98169
.98574
.98899
.921576
.923613
.925201
.926427
29

30.

ТАБЛИЦА НОРМИРОВАННОЙ ФУНКЦИИ
НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ
00
.926533
.927445
.928134
.928650
.930324
.933129
.935166.
.936631
.937674
.938409
.938922
.942765
.945190
.946833
.947934
.948665
.951460
.954587
.956602
.957888
.958699
.962067
.965208
01
.926636
.927523
.928193
.928694
.930646
.933363
.935335
.936752
.937759
.938469
.938964
.943052.
.945385
.946964
.948022
.948723
.951837
.954831
.956759
.957987
.95876I
.962453
.965446
02
.926736
.927599
.928250
.928736
.930957
.933590
935499
.936869
.937842
.938527
.940039
.943327
.945573
.947090
.948106
.948778
.952199
.955065
.956908
.958081
.958821
.962822
.965673
2.7
2.8
2.9
3.0
3.1
3.2
3.3
3.4
3.5
3.6
3.7
3.8
3.9
4.0
4.1
4.2
4.3
4.4
4.5
4.6
4.7
4.8
4.9
Пример:
Ф(3,39) = 0,9996505; Ф(0,98) = 0,8365.
03
.926833
.927673
.928305
.928777
.931260
.933810
.935658
.936982
.937922
.938583
.940426
.943593
.945753
.947211
.946186
.948832
.952545
.955288
.957051
.958172
.958877
.963173
.965889
04
.926928
.927744
.928359
.928817
.931553
.934024
.935811
.937091
.937999
.938637
.940799
.943848
.945926
.947327
.948263
.948882
.952876
.955502
.957187
.958258
.958931
.963508
.966094
05
.927020
.927814
.928411
.928856
.931836
.934230
.935959
.937197
.938074
.938689
.941158
.944094
.946092
.947439
.948338
.948931
.953193
.955706
.9573I8
.958340
.958983
.963827
.966289
06
.927110
.927882
.928462
.928893
.932112
.934429
.936103
.937299
.938146
.938739
.941504
.944331
.946253
.947546
.948409
.948978
.953497
.955902
.957442
.958419
.950320
.964131
.966475
07
.927197
.927948
.928511
.928930
.932378
.934623
.936242
.937398
.938215
.938787
.941838
.944558
.946406
.947649
.948477
.950226
.953788
.956089
.957561
.958494
.960789
.964420
.966652
08
.927282
.928012
.928559
.928965
.932636
.934810
.936376
.937493
.938282
.938834
.942159
.944777
.946554
.947748
.948542
.950655
.954066
.956268
.957675
.958566
.961235
.964696
.966821
30
09
.927365
.928074
.928605
.928999
.932868
.934991
.936505
.937585
.938347
.938879
.942568
.944988
.946696
.947843
.948605
.951066
.954332
.956439
.957784
.958634
.961661
.964958
.966981

31.

ИНТЕРПРЕТАЦИЯ СВЯЗИ МЕЖДУ ДВУМЯ
ПЕРЕМЕННЫМИ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
Диаграмма
Описание линейной связи
Величина rxy
Функциональная
(прямая)
+1,00
Случайная (прямая)
Около +0,50
Нет связи (ковариация
x и у covxy = 0)
0,00
Случайная
(обратная)
Около –0,50
Функциональная
(обратная)
–1,00
31

32.

ПАРАМЕТРЫ ЭМПИРИЧЕСКОЙ
ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
32
Параметры эмпирических функций распределения характеристик сопротивления усталости и
механических свойств крупных поковок нормализованной стали 40
Численное
значение
Параметр
Численное
значение
Параметр
Численное
значение
0 , МПа
S 0 , МПа
358
0, 2 , МПа
396
b , МПа
657
0 min , МПа
0 max , МПа
300
0, 2 min , МПа
310
419
0, 2 max , МПа
R 0 , МПа
119
R 0 , 2 , МПа
Параметр
V 0 , %
15,4
4,28
,%
S , %
23,7
min , %
16,4
max , %
R , %
31,0
V , %
2,07
14,6
8,74
S 0 , 2 , МПа
V 0 , 2 , %
41,5
S b , МПа
36,8
573
484
b min , МПа
b max , МПа
174
R b , МПа
178
10,24
,%
S , %
55,2
min , %
max , %
R , %
38,0
V , %
V b , %
751
5,59
aн , МДж/м2
2
S aн , МДж/м
0,795
0,565
26,0
aн min , МДж/м2
aн max , МДж/м2
2
Raн , МДж/м
11,11
Vaн , %
6,14
64,0
0,107
1,075
0,515
13,46

33.

СТАТИСТИЧЕСКИЕ ЗАВИСИМОСТИ
Оценка силы корреляционных связей между пределом выносливости и
характеристиками механических свойств стали 40
Материал
Связь
Значение коэффициента
корреляции
Уравнение линии регрессии
Сталь 40
0(ан)
0,9994
0 266,3 112,4ан
0( 0,2)
0,9996
0 224,7 0,338 0,2
0( b)
0,9995
0 78,5 0,426 b
0( )
0,9989
0 202 6,587
0( )
0,9991
0 425 9604 2,3 60 2
Вероятностные соотношения между пределом выносливости и другими характеристиками
механических свойств стали 40
Вероятность Р
0
b
0
0 ,2
0 МПа
,
%
0 МПа
,
%
0
МПа
,
ан МДж/м2
0,01
0,50
0,99
0,557
0,543
0,540
1,009
0,906
0,805
17,9
14,9
13,6
8,28
6,40
6,26
537
448
359
33

34.

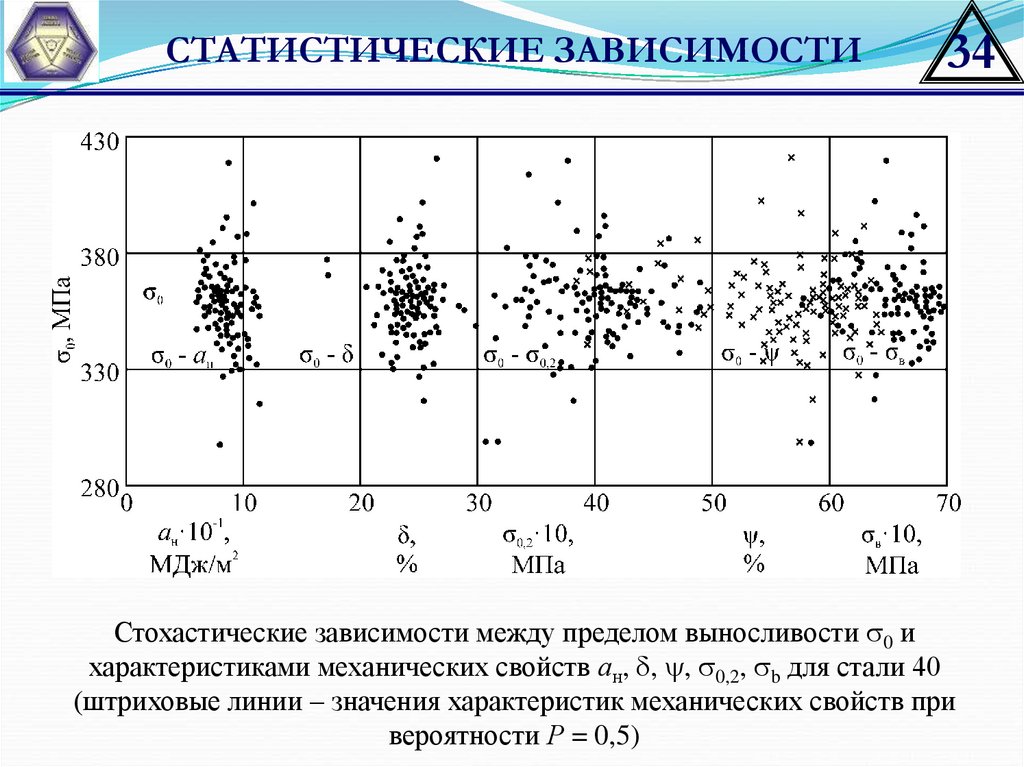
СТАТИСТИЧЕСКИЕ ЗАВИСИМОСТИ
34
Стохастические зависимости между пределом выносливости 0 и
характеристиками механических свойств ан, , , 0,2, b для стали 40
(штриховые линии – значения характеристик механических свойств при
вероятности Р = 0,5)

35.

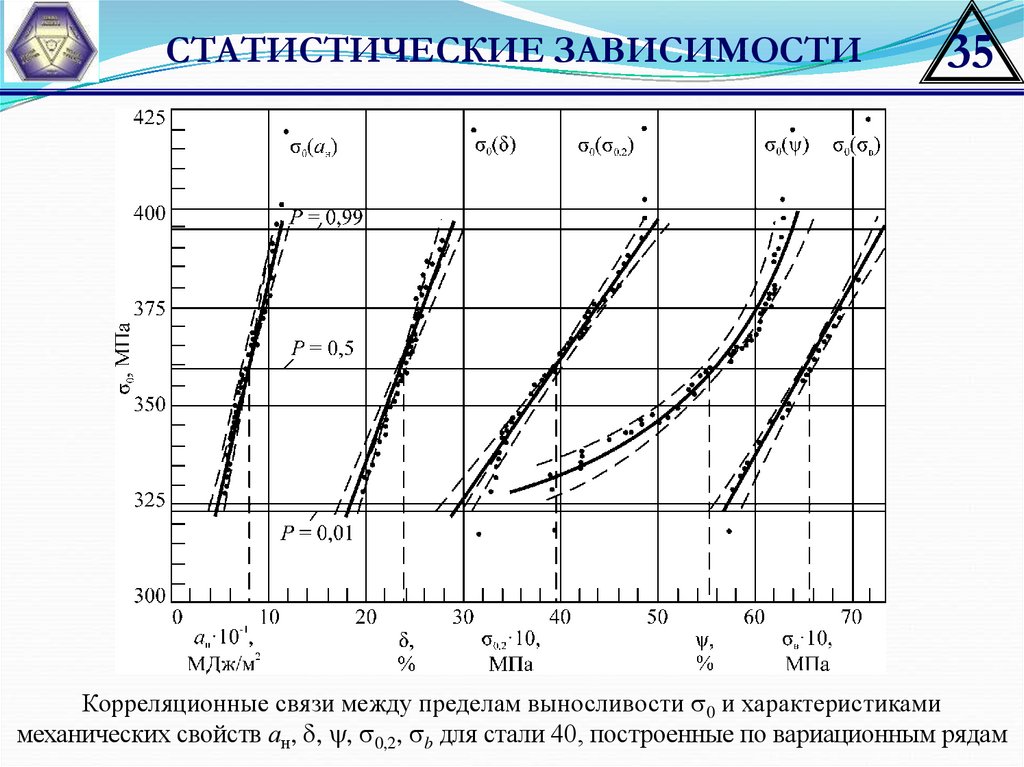
СТАТИСТИЧЕСКИЕ ЗАВИСИМОСТИ
35
Корреляционные связи между пределам выносливости 0 и характеристиками
механических свойств ан, , , 0,2, b для стали 40, построенные по вариационным рядам