Основные типы статистических распределений случайных величин, используемых в теории надежности

1.

ОСНОВНЫЕ ТИПЫ СТАТИСТИЧЕСКИХ
РАСПРЕДЕЛЕНИЙ СЛУЧАЙНЫХ ВЕЛИЧИН,
ИСПОЛЬЗУЕМЫХ В ТЕОРИИ НАДЕЖНОСТИ

2.

Распределение Вейбулла
При распределении Вейбулла (Вейбулла-Гнеденко) вероятность безотказной
работы в интервале времени (0, t) имеет вид:
t
P(t ) exp( ), t 0; a 0; 0
a
где а – параметр масштаба
- параметр формы
Функция p(t) для распределения
Вейбулла:
Исходя из формулы для
определения р(t), плотность
вероятности отказов f(t) будет
определяться:
f (t ) P (t )
1
a
t
t
exp( )
a
f(t)

3.

Среднее время безотказной работы (наработка на отказ)
Tср P(t )dt e
0
t
a
dt
0
Интенсивность отказов для распределения Вейбулла
t
t exp( )
f (t ) a
1
a
(t )
t
t
P(t )
a
exp( )
a
1
где t ≥ 0 ; a > 0 ; δ > 0
λ(t): при δ<1 монотонно убывает,
при δ=1 – λ=const,
при δ>1 – λ(t) монотонно возрастает

4.

ЭКСПОНЕНЦИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
Экспоненциальное распределение (ЭР) является частным
случаем распределения Вейбулла при δ=1. При этом:
В этом случае (t) = , где – некоторая постоянная величина
Из
выражения определения интенсивности отказов для
распределения Вейбула следует, что при δ=1 λ(t)≡λ
Распределение
вероятности отказов, соответствующее
такой
характеристике,
называется
экспоненциальным
верно и обратное утверждение: если λ(t) постоянна, то
вероятность
Р(t),
как
функция
времени,
подчиняется
экспоненциальному закону, →
нормальная
эксплуатация
устройств характеризуется ЭР интервала безотказной работы.

5.

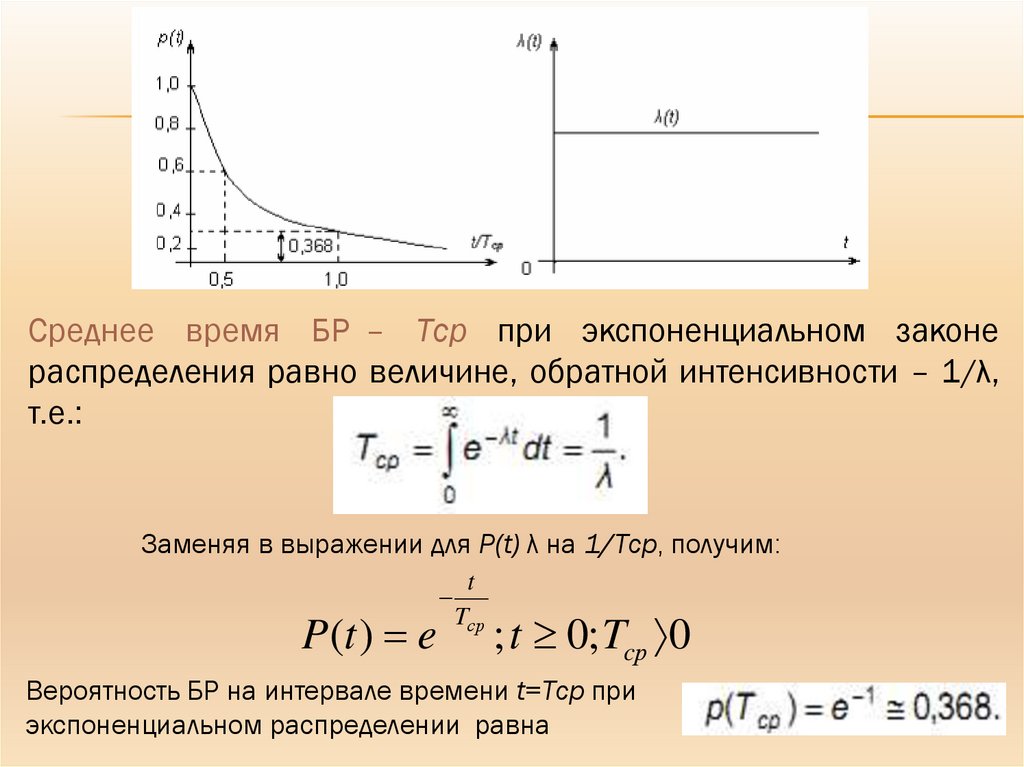
Среднее время БР – Tср при экспоненциальном законе
распределения равно величине, обратной интенсивности – 1/λ,
т.е.:
Заменяя в выражении для P(t) λ на 1/Tср, получим:
P (t ) e
t
Tср
; t 0; Tcр 0
Вероятность БР на интервале времени t=Tср при
экспоненциальном распределении равна

6.

Плотность распределения наработки на отказ f(t) для ЭР соответственно
равна:
t
f (t ) P (t ) e
Вычислим дисперсию времени БР для экспоненциального закона:
Таким образом, дисперсия времени БР:
Найдем условную вероятность того, что для экспоненциальной модели
устройство проработает безотказно на интервале времени t, после того как оно
безотказно проработало на интервале τ.
В этом случае имеем:
Отсюда следует важный вывод: для экспоненциального закона
распределения вероятности БР распределение времени БР не
зависит от того, сколько времени оно проработало до начала
отсчета от момента первого включения.

7.

Основные показатели надежности для экспоненциального
распределения вероятности отказа
Показатель
Точное значение
Приближенное
значение
P(t) = P(t, t+t0)
e-λt
1 - λt
Q(t) = Q(t, t+t0)
1 - e-λt
λt
T
1/λ
---
f(t)
λe-λt
λ (1 – λt)
λ(t)
λ
---
Экспоненциальное распределение уникально в том смысле, что ожидаемый
характер отказов никак не меняется на протяжении всего срока службы
изделия.
Предшествующее использование прибора никак не влияет на его
работоспособность в последующие моменты времени, а определяется
длиной интервала t.

8.

Гамма-процентная наработка до отказа при экспоненциальном
распределении:
P(t γ ) e
λt
100
γ
1 γ
t γ ln
t γ T ln
100
λ 100
γ
Положим = 90 %. Это означает, что не менее 90 % приборов
из рассматриваемой нами совокупности должны безотказно
работать в течение времени t (или вероятность безотказной
работы совокупности приборов в течение времени t должна быть
не ниже 0,9). С учетом этого получим
100
t 90 T ln
0,105T
90
Полученный результат показывает, что гамма-процентная
наработка при = 90 % составит всего примерно 0,1 от
средней наработки до отказа

9.

Графическое изображение зависимости показателей надежности от
времени
Вид
распределе-ния
Экспоненциальное
ВейбуллаГнеденко
Нормальное
Показатели надежности
f(t)
Q(t)
P(t)
λ(t)

10.

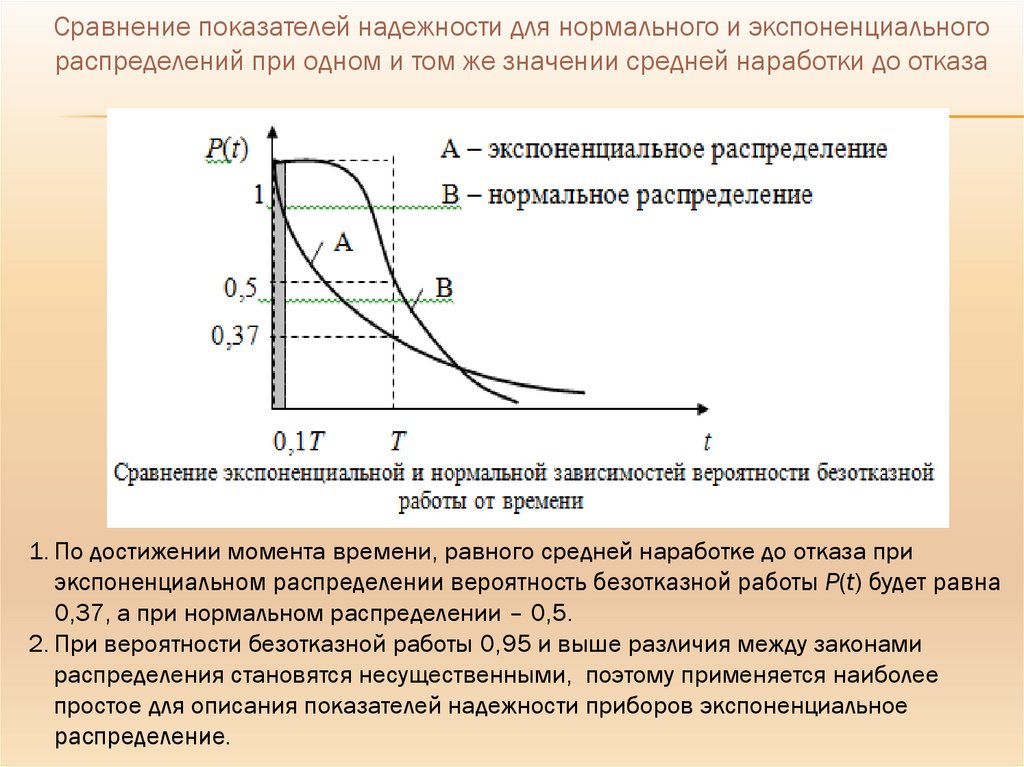
Сравнение показателей надежности для нормального и экспоненциального
распределений при одном и том же значении средней наработки до отказа
1. По достижении момента времени, равного средней наработке до отказа при
экспоненциальном распределении вероятность безотказной работы Р(t) будет равна
0,37, а при нормальном распределении – 0,5.
2. При вероятности безотказной работы 0,95 и выше различия между законами
распределения становятся несущественными, поэтому применяется наиболее
простое для описания показателей надежности приборов экспоненциальное
распределение.

11.

Распределение Релея
При распределении Релея вероятность безотказной работы на
интервале (0,t) равна: (рис.а)
где: σ – параметр распределения Релея, который одновременно
является модой этого распределения.
Мода непрерывного распределения есть точка максимума плотности
распределения вероятности f(t).
Мода дискретного распределения есть такое спектральное значение ξm,
при котором предшествующие и последующие спектральные значения
имеют вероятности, меньшие, чем p(ξm).
плотность распределения наработки на отказ равна (рис. б):
t2
f (t ) P (t ) 2 exp( 2 )
2
t

12.

Распределение Релея
f (t )
t
(t )
2
P(t )
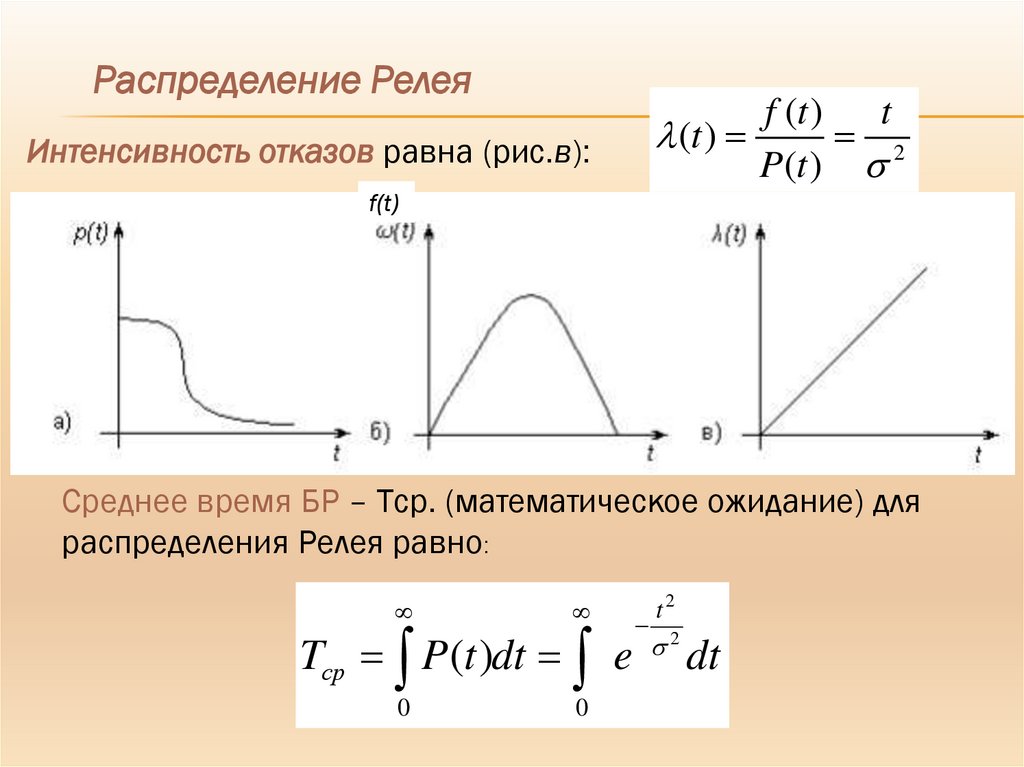
Интенсивность отказов равна (рис.в):
f(t)
Среднее время БР – Tср. (математическое ожидание) для
распределения Релея равно:
Tср P (t )dt e
0
0
t2
2
dt

13.

Гамма-распределение
При Гамма-распределении (ГР) плотность распределения
наработки на отказ равна:
f (t )
где Г(r) – полная гамма-функция.
02
Г (r )
t r 1 exp( 0t )
В теории надежности ГР обычно используется при целом значении r.
Если r =1, то ГР вырождается в экспоненциальное распределение.
Если r – целое число >1 , то ГР является распределением суммы
независимых случайных величин, каждая из которых имеет
экспоненциальное распределение с параметром:
Гамма-распределение при целом значении r иногда
называют распределением Эрланга

14.

вероятность БР на интервале (0,t) равна (рис.а):
Плотность распределения наработки на
отказ в этом случае (рис. б):
f (t ) 0
0 t r 1
(r 1)!
exp( 0t )
Среднее время БР и дисперсия
времени БР соответственно равны:
Интенсивность отказов равна (рис.в):

15.

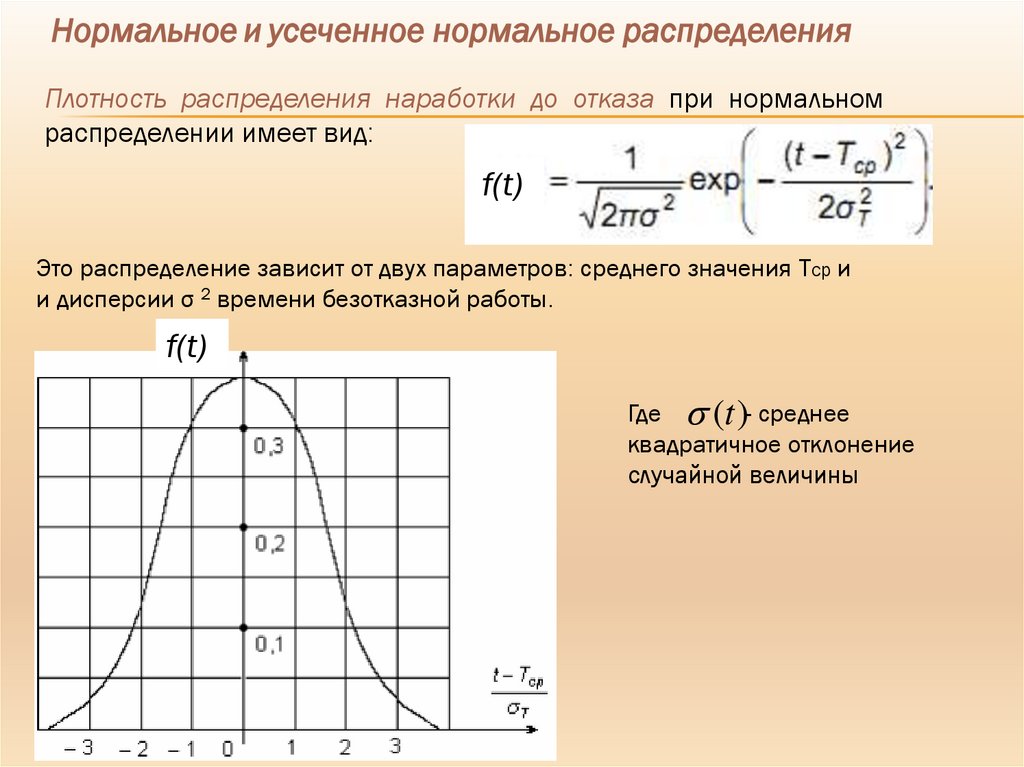
Нормальное и усеченное нормальное распределения
Плотность распределения наработки до отказа при нормальном
распределении имеет вид:
f(t)
Это распределение зависит от двух параметров: среднего значения Tср и
и дисперсии σ 2 времени безотказной работы.
f(t)
Где (t )- среднее
квадратичное отклонение
случайной величины

16.

Усеченное нормальное распределение
В этом случае нарушается условие нормирования плотности распределения:
когда f(t) =0 при t<0
f(t)
для сохранения условия
нормирования плотности
распределения, вводится
нормирующий множитель С,
определяющийся из условия, что
площадь под кривой плотности
распределения =1
f (t ) Cf (t )
1
2
C
exp
(t Tср ) dt 1
2
2
2 0
2
1

17.

Для усеченного нормального распределения плотность
распределения наработки на отказ:
f(t)
(1)
Функция надежности будет равна:
f(t)dt
(2)

18.

Из выражений (1) и (2) находим функцию интенсивности отказов λ(t)
при усеченном нормальном законе распределения длительности БР. Она
имеет вид:
Графики функции надежности и интенсивности отказов
при усеченном нормальном законе распределения.

19.

При больших значениях t ИО в рассматриваемом случае возрастает по
линейному закону:
Следует иметь в виду, что параметр Tср. усеченного нормального
распределения не равен среднему времени БР при использовании этого
распределения в качестве модели безотказности.
В этом случае среднее время БР (Tср)ус будет равно: