Похожие презентации:
Тела вращения
1. ТЕЛА ВРАЩЕНИЯ
2. Теория. Примеры тел вращения
ТЕОРИЯ.ПРИМЕРЫ ТЕЛ ВРАЩЕНИЯ
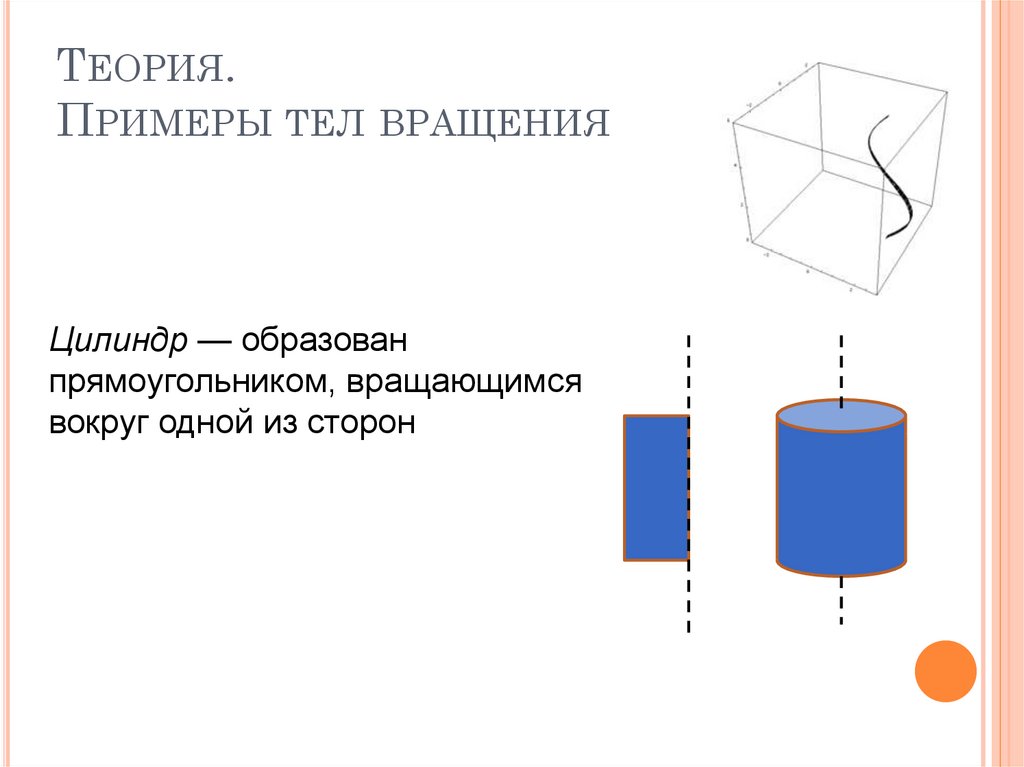
Цилиндр — образован
прямоугольником, вращающимся
вокруг одной из сторон
3. Теория. Примеры тел вращения
ТЕОРИЯ.ПРИМЕРЫ ТЕЛ ВРАЩЕНИЯ
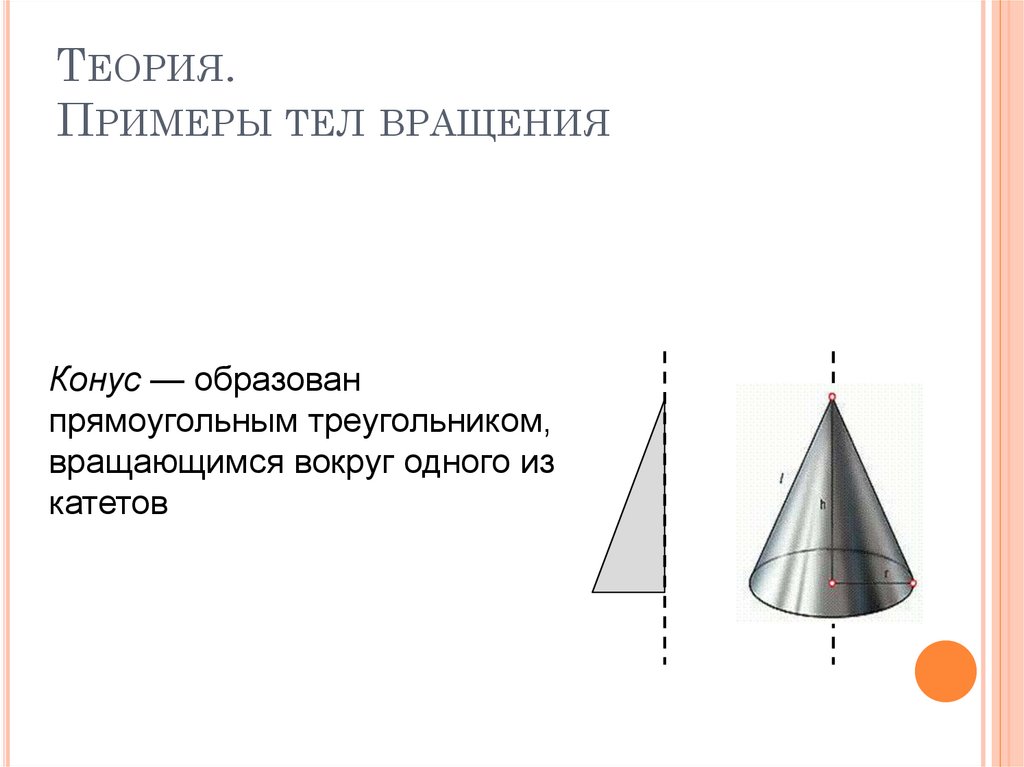
Конус — образован
прямоугольным треугольником,
вращающимся вокруг одного из
катетов
4. Теория. Примеры тел вращения
ТЕОРИЯ.ПРИМЕРЫ ТЕЛ ВРАЩЕНИЯ
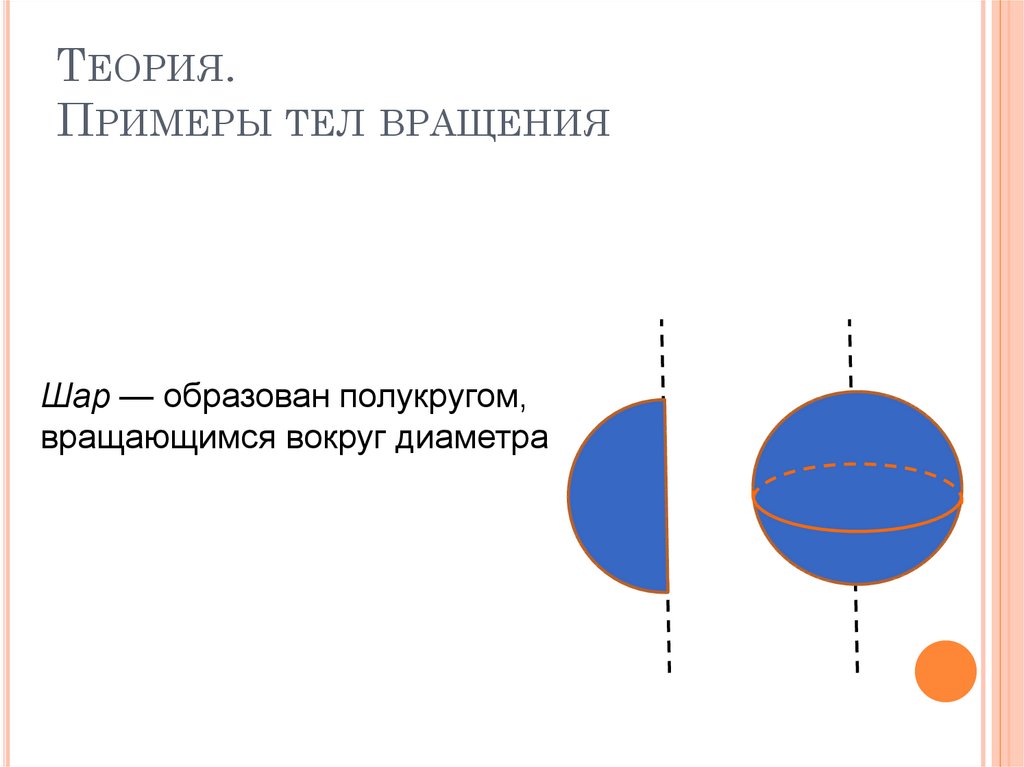
Шар — образован полукругом,
вращающимся вокруг диаметра
5. Теория. Цилиндр
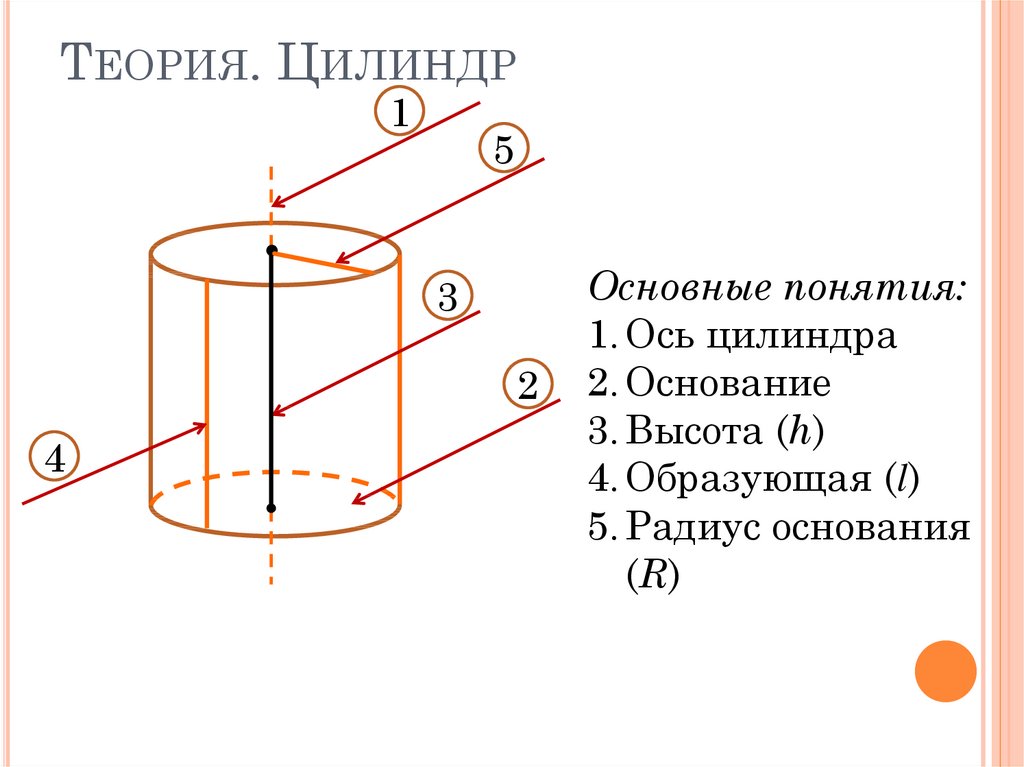
ТЕОРИЯ. ЦИЛИНДР1
.
5
3
2
4
.
Основные понятия:
1. Ось цилиндра
2. Основание
3. Высота (h)
4. Образующая (l)
5. Радиус основания
(R)
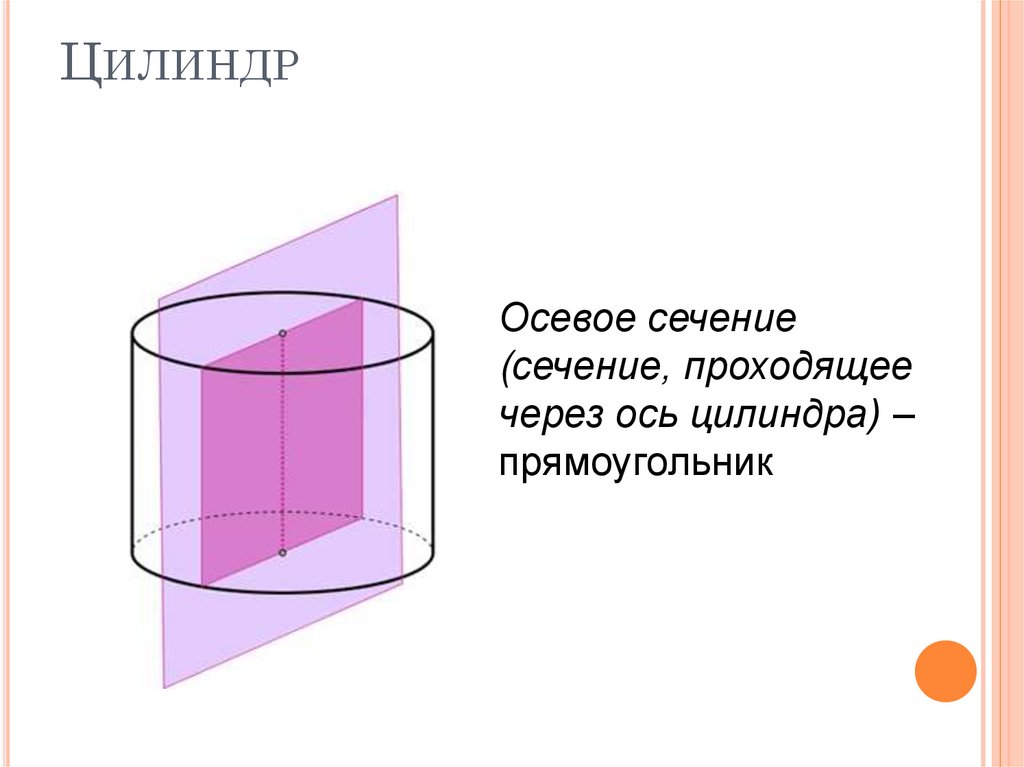
6. Цилиндр
ЦИЛИНДРОсевое сечение
(сечение, проходящее
через ось цилиндра) –
прямоугольник
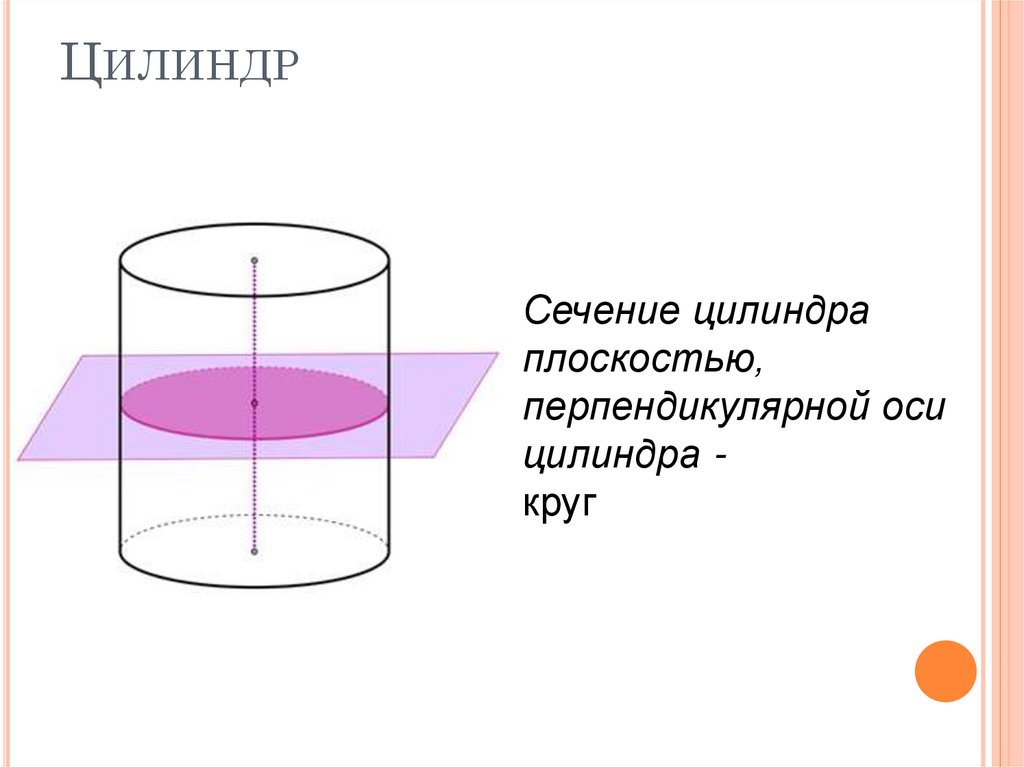
7. Цилиндр
ЦИЛИНДРСечение цилиндра
плоскостью,
перпендикулярной оси
цилиндра круг
8. Цилиндр
ЦИЛИНДРФормулы:
S осн R
2
- площадь основания
S бок 2 Rh
- площадь боковой
поверхности
V R 2 h
- объем
R радиус; h высота
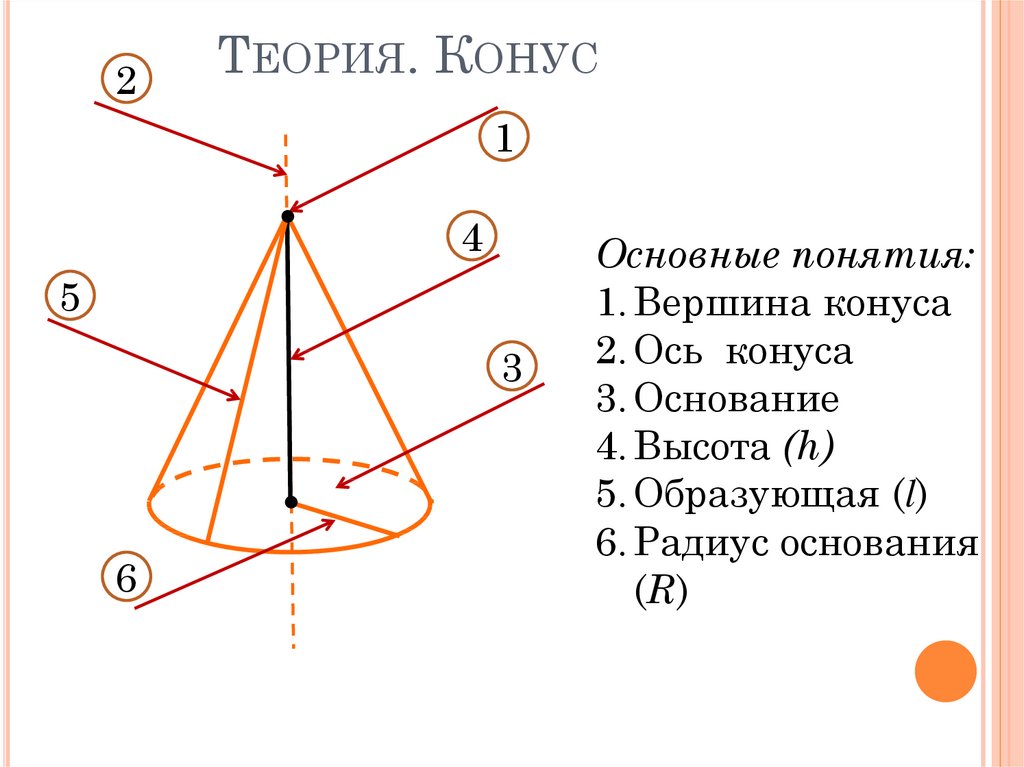
9. Теория. Конус
2ТЕОРИЯ. КОНУС
.
1
4
5
3
.
6
Основные понятия:
1. Вершина конуса
2. Ось конуса
3. Основание
4. Высота (h)
5. Образующая (l)
6. Радиус основания
(R)
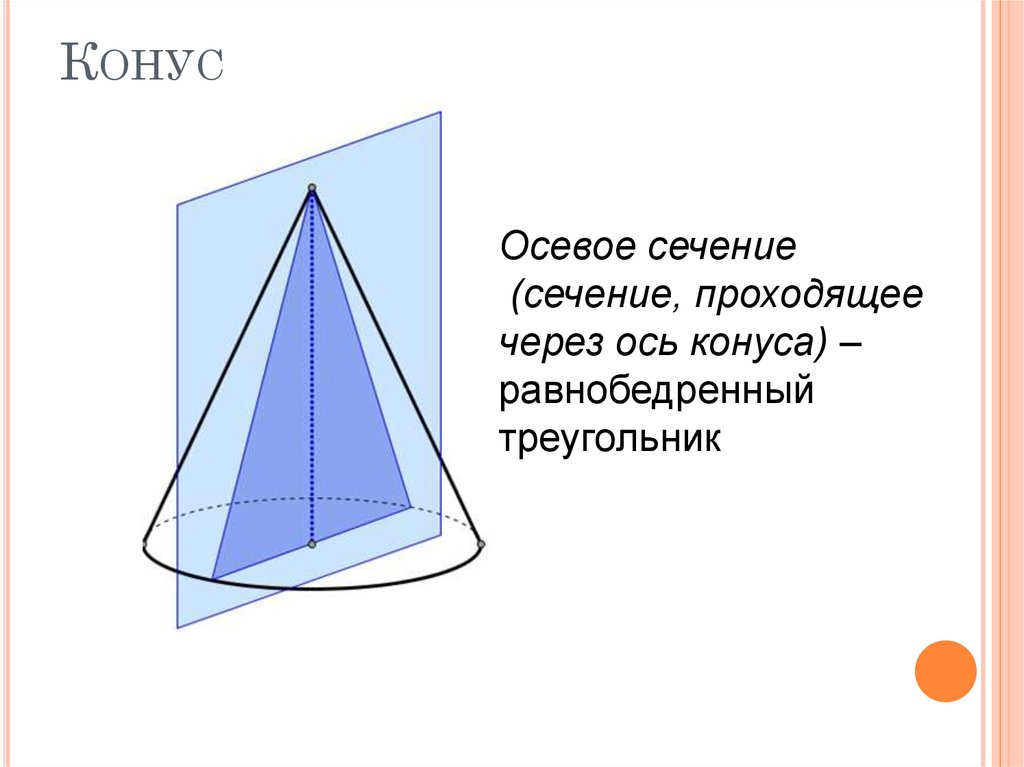
10. Конус
КОНУСОсевое сечение
(сечение, проходящее
через ось конуса) –
равнобедренный
треугольник
11. Конус
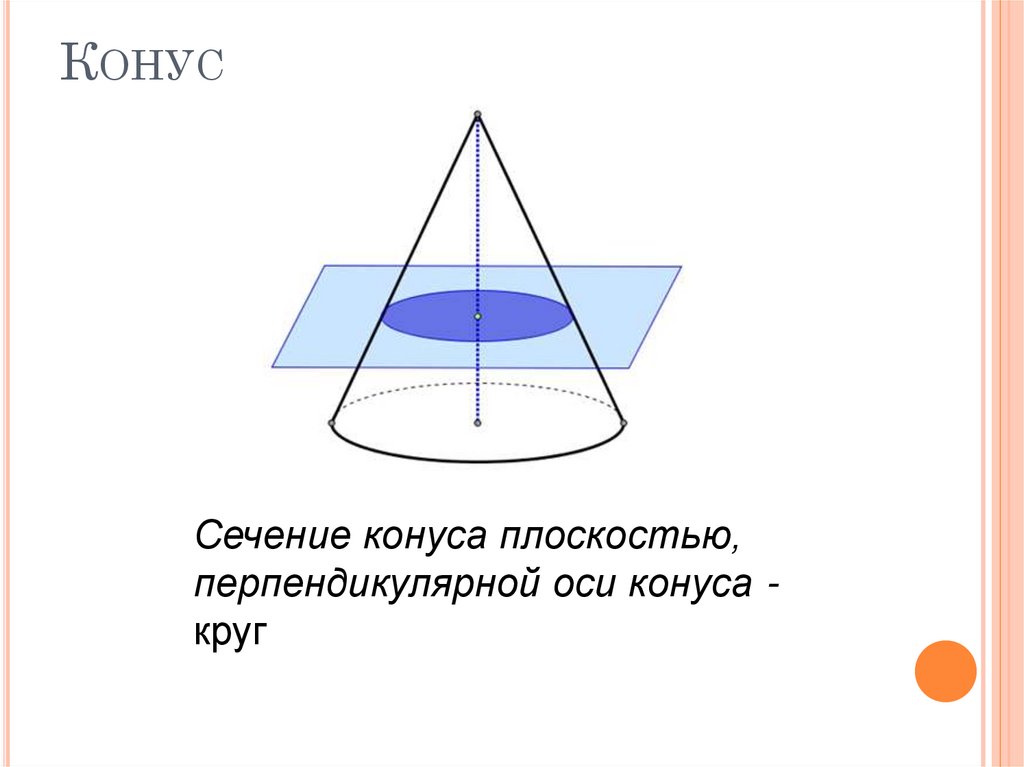
КОНУССечение конуса плоскостью,
перпендикулярной оси конуса круг
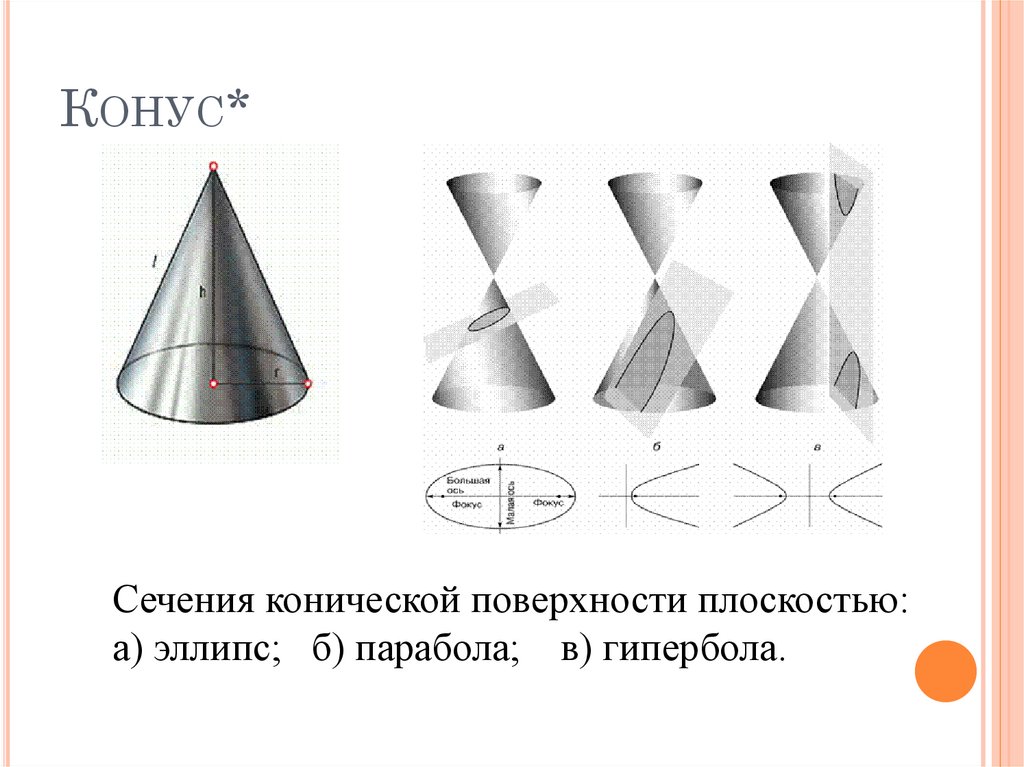
12. Конус*
КОНУС*Сечения конической поверхности плоскостью:
а) эллипс; б) парабола; в) гипербола.
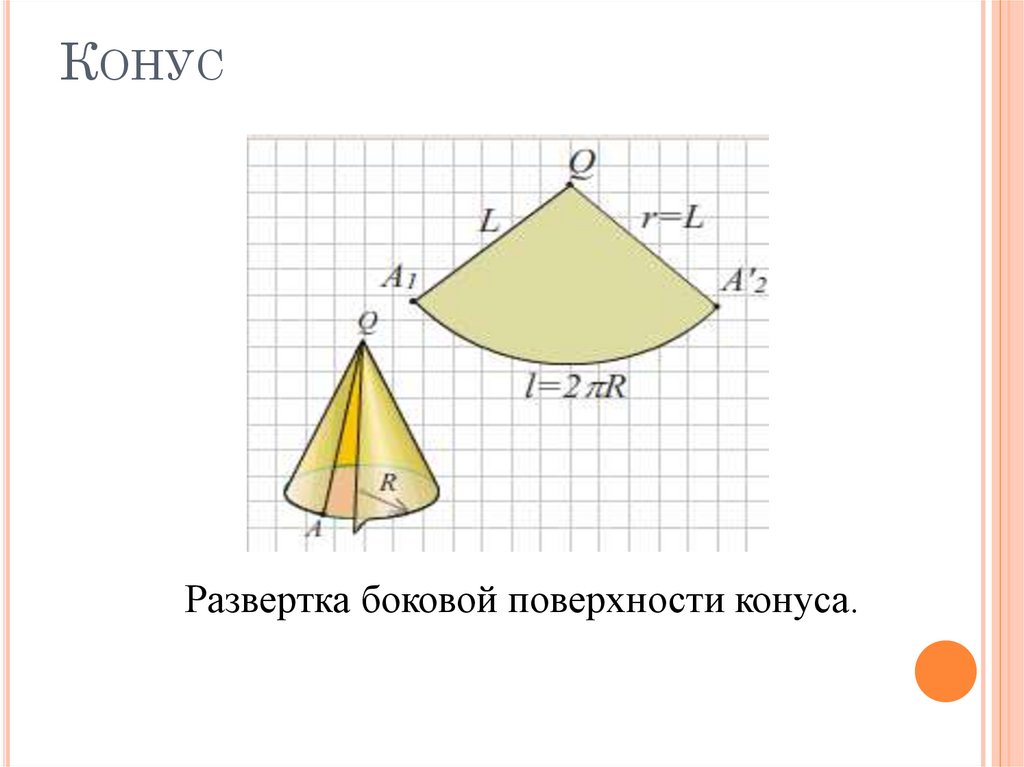
13. Конус
КОНУСРазвертка боковой поверхности конуса.
14. Конус
КОНУСФормулы:
S осн R
2
- площадь основания
Sбок Rl
- площадь боковой
поверхности
1 2
V R h
3
- объем
R радиус; h высота; l образующая
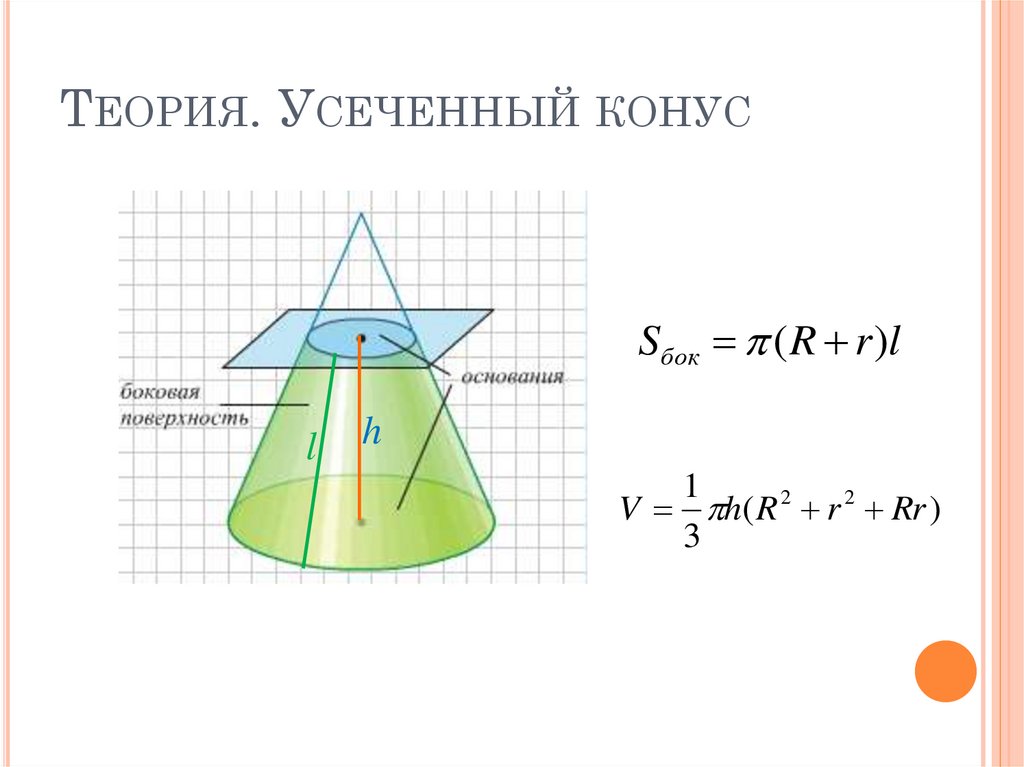
15. Теория. Усеченный конус
ТЕОРИЯ. УСЕЧЕННЫЙ КОНУСSбок ( R r )l
l
h
1
V h( R 2 r 2 Rr )
3
16. Теория. Сфера и шар
ТЕОРИЯ. СФЕРА И ШАРт.О – центр
сферы
R - радиус
Площадь поверхности:
S 4 R 2
Объём:
4 3
V R
3
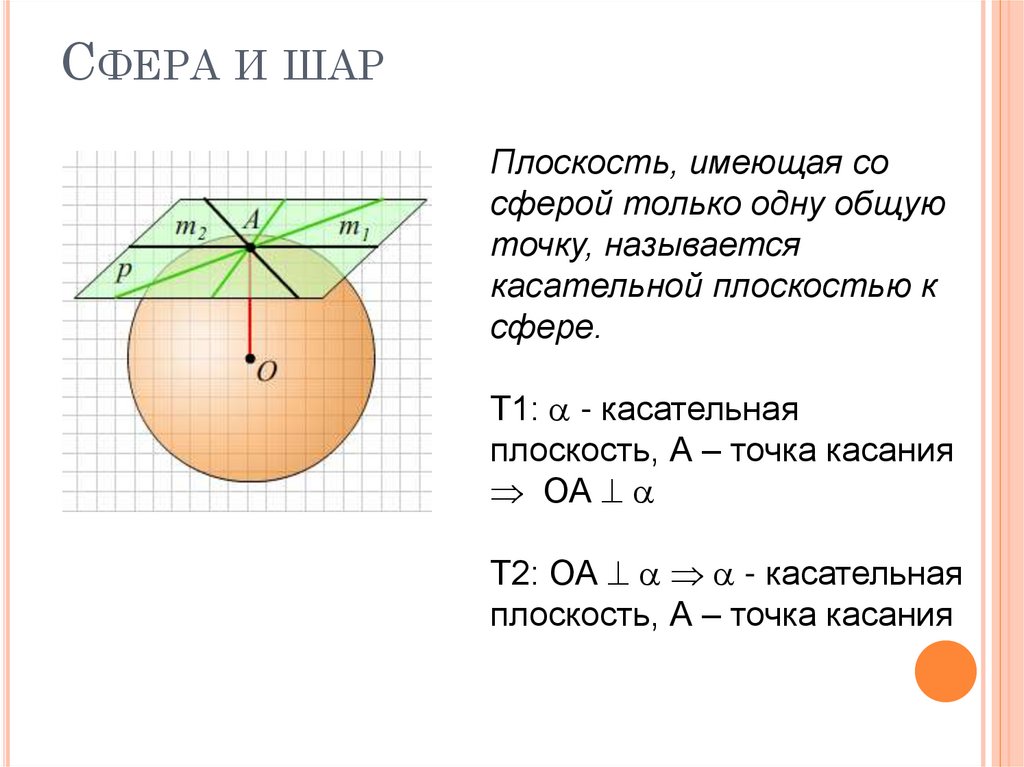
17. Сфера и шар
СФЕРА И ШАРПлоскость, имеющая со
сферой только одну общую
точку, называется
касательной плоскостью к
сфере.
Т1: - касательная
плоскость, А – точка касания
ОА
Т2: ОА - касательная
плоскость, А – точка касания
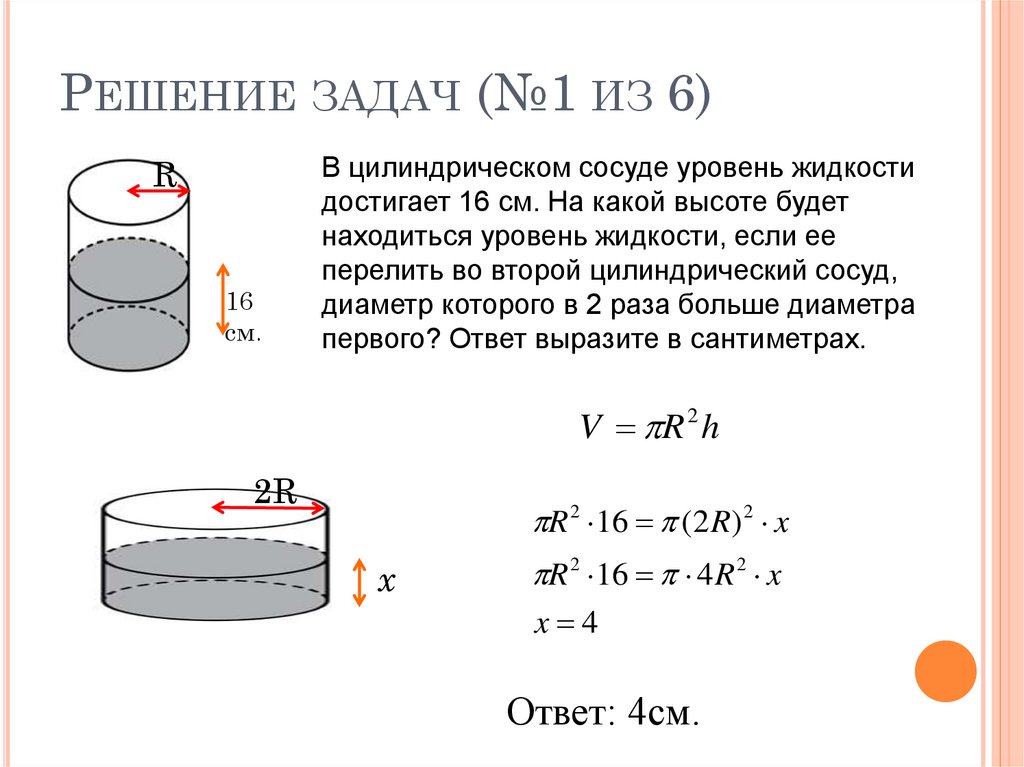
18. Решение задач (№1 из 6)
РЕШЕНИЕ ЗАДАЧ (№1 ИЗ 6)R
16
см.
В цилиндрическом сосуде уровень жидкости
достигает 16 см. На какой высоте будет
находиться уровень жидкости, если ее
перелить во второй цилиндрический сосуд,
диаметр которого в 2 раза больше диаметра
первого? Ответ выразите в сантиметрах.
V R 2 h
2R
R 2 16 (2 R) 2 x
x
R 2 16 4 R 2 x
x 4
Ответ: 4см.
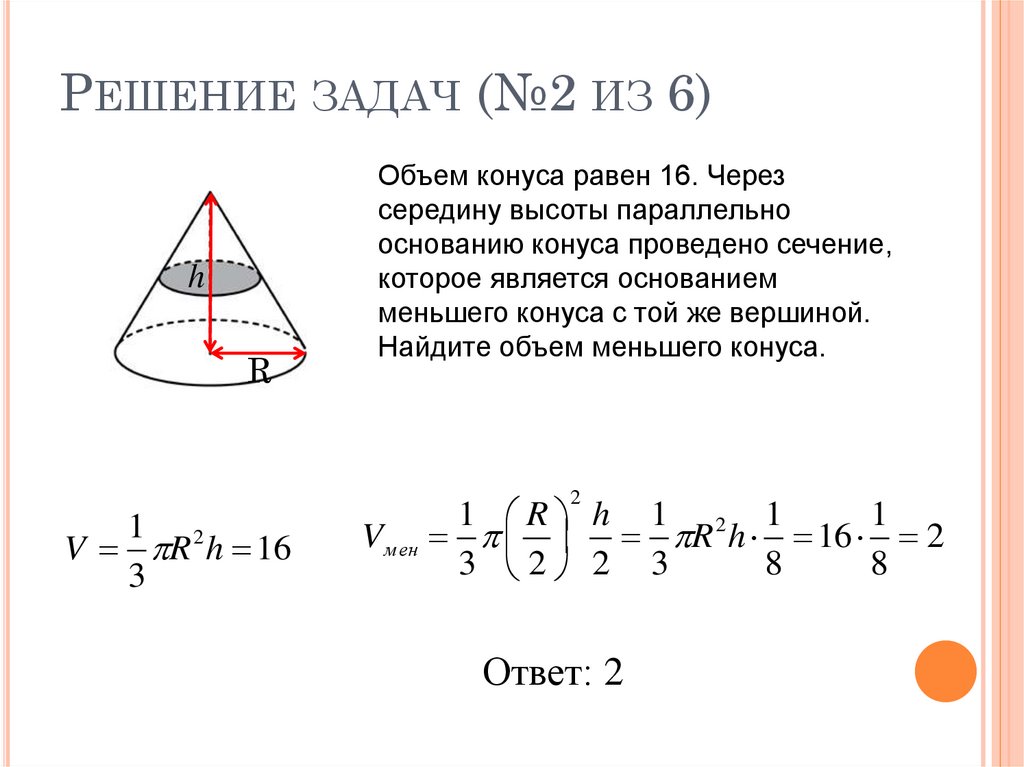
19. Решение задач (№2 из 6)
РЕШЕНИЕ ЗАДАЧ (№2 ИЗ 6)h
R
Объем конуса равен 16. Через
середину высоты параллельно
основанию конуса проведено сечение,
которое является основанием
меньшего конуса с той же вершиной.
Найдите объем меньшего конуса.
2
1 2
V R h 16
3
1 R h 1 2 1
1
Vм ен R h 16 2
3 2 2 3
8
8
Ответ: 2
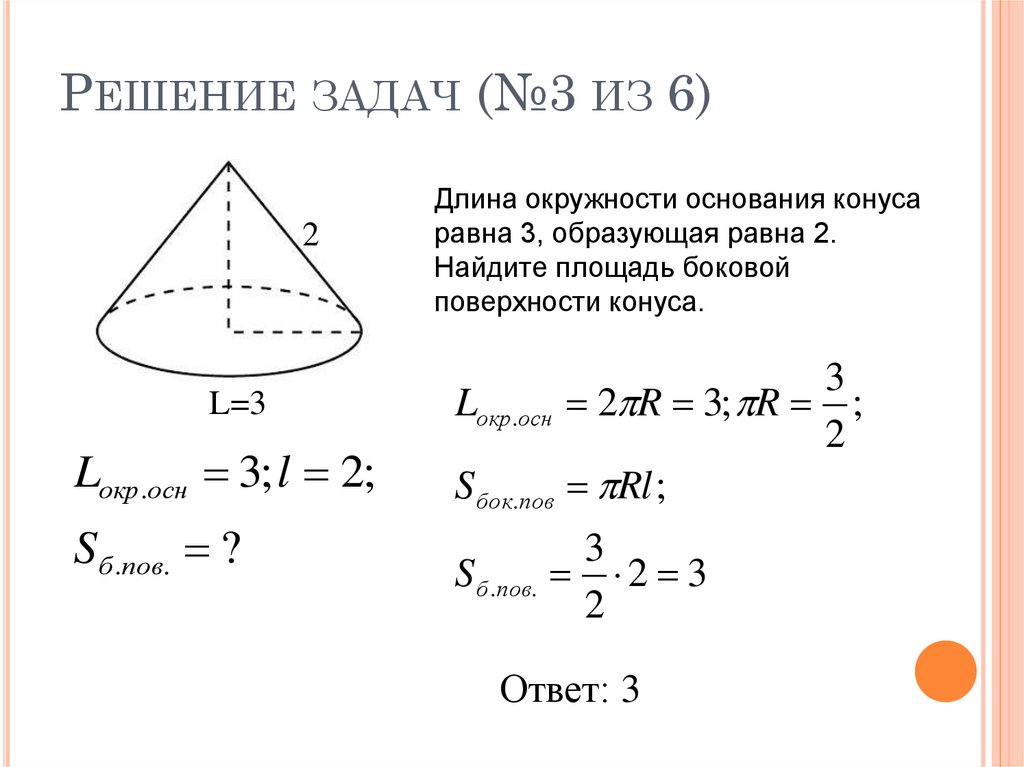
20. Решение задач (№3 из 6)
РЕШЕНИЕ ЗАДАЧ (№3 ИЗ 6)2
L=3
Lокр.осн 3; l 2;
S б .пов. ?
Длина окружности основания конуса
равна 3, образующая равна 2.
Найдите площадь боковой
поверхности конуса.
3
Lокр.осн 2 R 3; R ;
2
S бок.пов Rl ;
S б .пов.
3
2 3
2
Ответ: 3
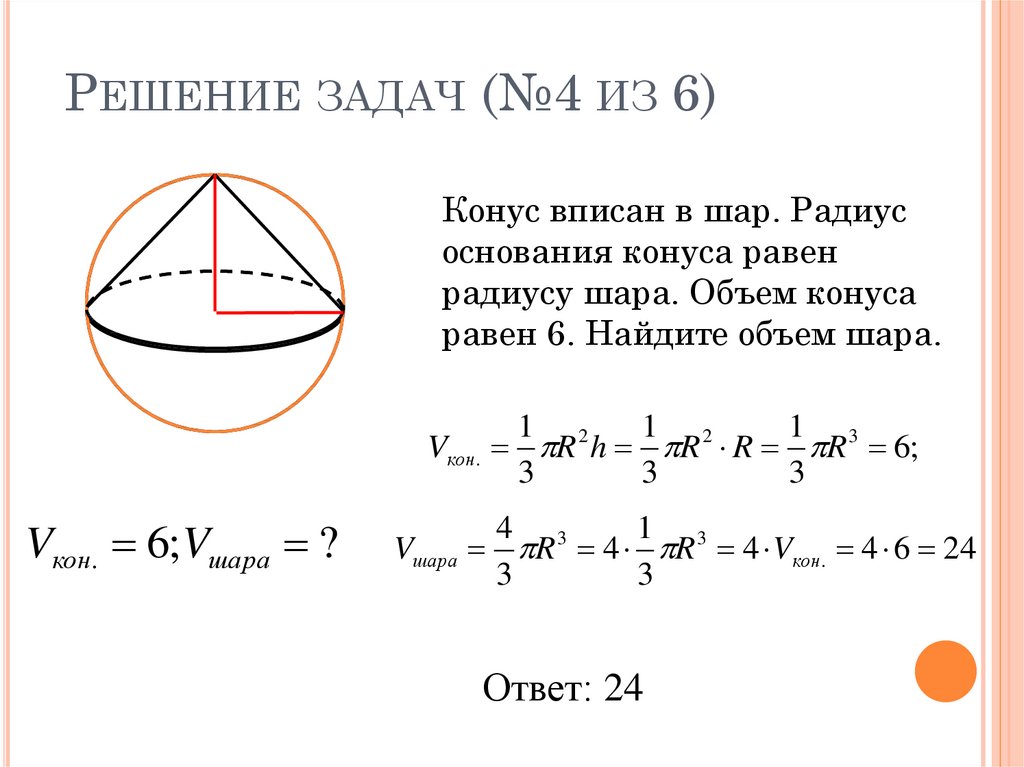
21. Решение задач (№4 из 6)
РЕШЕНИЕ ЗАДАЧ (№4 ИЗ 6)Конус вписан в шар. Радиус
основания конуса равен
радиусу шара. Объем конуса
равен 6. Найдите объем шара.
Vкон.
Vкон. 6;Vшара ?
Vшара
1 2
1 2
1 3
R h R R R 6;
3
3
3
4 3
1 3
R 4 R 4 Vкон. 4 6 24
3
3
Ответ: 24
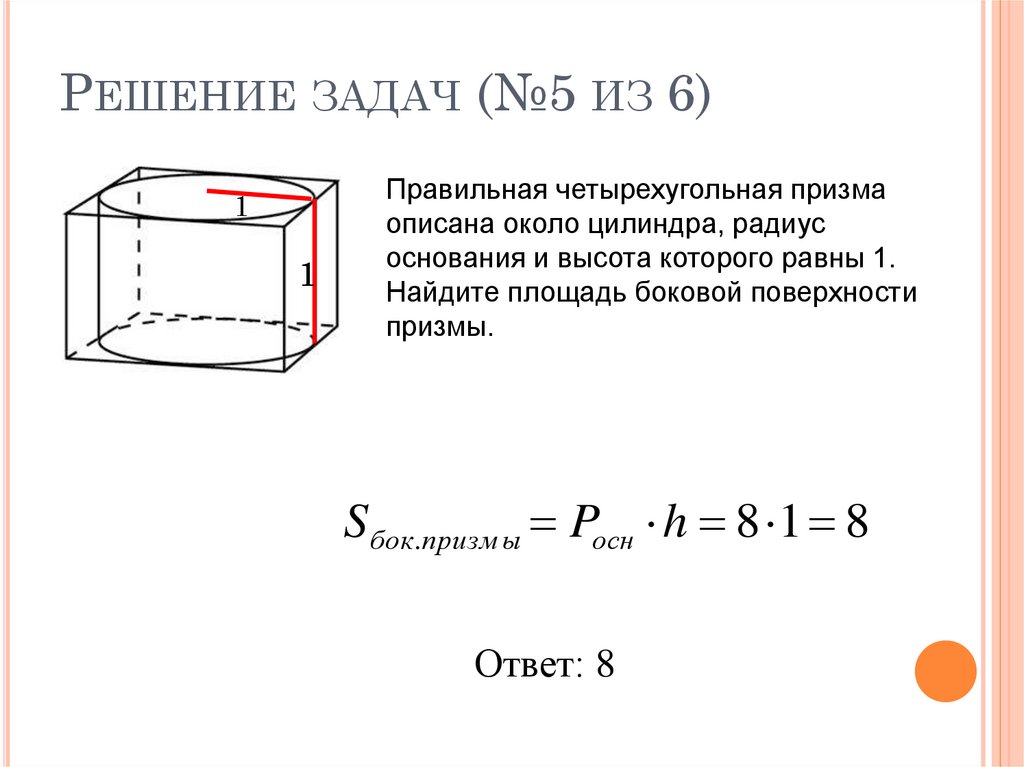
22. Решение задач (№5 из 6)
РЕШЕНИЕ ЗАДАЧ (№5 ИЗ 6)1
1
Правильная четырехугольная призма
описана около цилиндра, радиус
основания и высота которого равны 1.
Найдите площадь боковой поверхности
призмы.
S бок.призм ы Pосн h 8 1 8
Ответ: 8
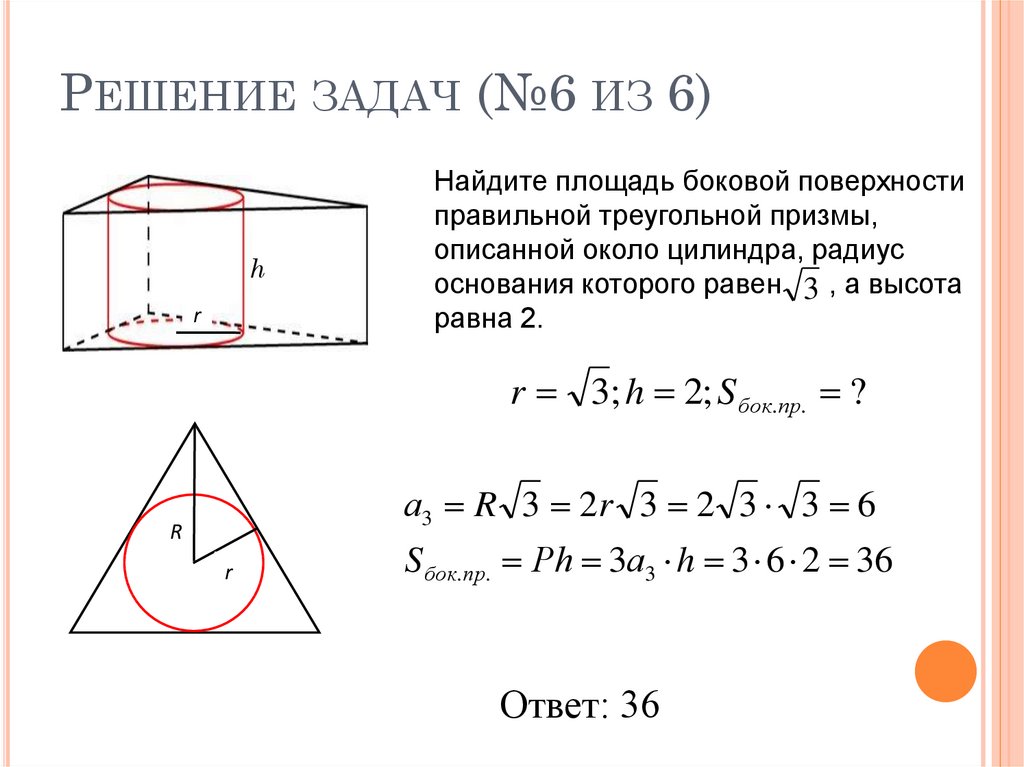
23. Решение задач (№6 из 6)
РЕШЕНИЕ ЗАДАЧ (№6 ИЗ 6)h
r
Найдите площадь боковой поверхности
правильной треугольной призмы,
описанной около цилиндра, радиус
основания которого равен 3 , а высота
равна 2.
r 3; h 2; S бок.пр. ?
а3 R 3 2r 3 2 3 3 6
R
rr
S бок.пр. Рh 3а3 h 3 6 2 36
Ответ: 36
24. Самостоятельная работа
САМОСТОЯТЕЛЬНАЯ РАБОТА1. Радиус основания цилиндра равен 2, высота
равна 3. Найдите площадь боковой
поверхности цилиндра, деленную на .
2. Площадь большого круга шара равна 3.
Найдите площадь поверхности шара.
3.
Площадь боковой поверхности конуса в два
раза больше площади основания. Найдите
угол между образующей конуса и плоскостью
основания. Ответ дайте в градусах.
Дополнительны
е задачи
Перейти к
проверке
25. Самостоятельная работа (задача 1)
САМОСТОЯТЕЛЬНАЯ РАБОТА (ЗАДАЧА1)
Радиус основания цилиндра
равен 2, высота равна 3. Найдите
площадь боковой поверхности
цилиндра, деленную на .
R 2; h 3;
S бок
?
S бок 2 Rh 2 2 3 12 ;
S бок
12
12
Ответ: 12
26. Самостоятельная работа (задача 2)
САМОСТОЯТЕЛЬНАЯ РАБОТА (ЗАДАЧА2)
Площадь большого круга шара
равна 3. Найдите площадь
поверхности шара.
S круга 3;
S кр R 2 3;
S пов.шара ?
S пов.шара 4 R 2 4 3 12
Ответ: 12
27. Самостоятельная работа (задача 3)
САМОСТОЯТЕЛЬНАЯ РАБОТА (ЗАДАЧА3)
A
C
B
S бок
2; ABC ?
S осн
Площадь боковой поверхности
конуса в два раза больше
площади основания. Найдите
угол между образующей конуса
и плоскостью основания. Ответ
дайте в градусах
S бок Rl
2 2;
S осн R
l
2;
R
BAC 30 ; ABC 60
Ответ: 60 .
28. Дополнительные задачи
ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ1. Осевое сечение конуса прямоугольный треугольник.
Найдите площадь боковой поверхности конуса, если его
радиус основания равен R.
2. Цилиндр образован вращением прямоугольника
вокруг одной из его сторон. Выразите объем цилиндра
через площадь S прямоугольника и длину С окружности
основания цилиндра.
Продолжение
доп. задач
Вернуться к
с/р
29. Дополнительные задачи
ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ3. В щар с единичным радиусом вписан конус, образующая
которого равна 3.
Найдите величину угла при вершине осевого сечения
конуса.
4. В цилиндр, радиус основания которого равен 6, вписан
конус. Основание конуса совпадает с основанием
цилиндра, а вершина конуса совпадает с центром верхнего
основания цилиндра. Площадь боковой поверхности
конуса равна 60 . Найдите площадь боковой поверхности
цилиндра.
Вернуться к
с/р











 Математика
Математика








