Похожие презентации:
Показательная функция, ее графики и свойства
1. Показательная функция, ее график и свойства
Составить конспект по теме (определение,примеры, графики, свойства,
рассмотренные упражнения)
Выполнить задание
Работу выслать до 21-00 14.05.2020
2. Определение показательной функции
Показательной функцией называетсях
функция у = а , где а – заданное число,
а>0, a ≠ 1.
Примеры:
1
у
3
х
у 0, 4
у 2
х
у 5
х
у
3
х
х
3. График показательной функции у = а , а>1(график называется экспонента)
График показательной функциих
у = а , а>1(график называется экспонента)
Построим график
показательной функции
У
у=2х
у=4х
у 2 , а 2.
х
В этой же системе
координат построим
графики функций
у=(1,5)х
у 4 , а 4
х
у 1,5 , а 1,5.
х
1
0
Х
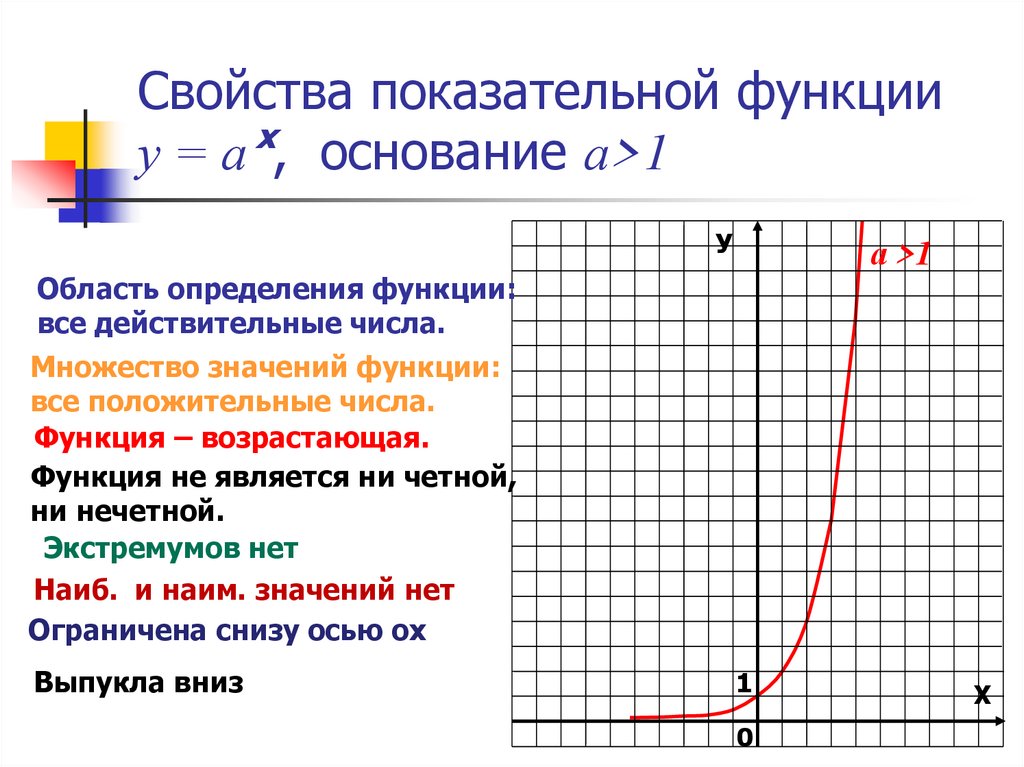
4. Свойства показательной функции у = а , основание а>1
Свойства показательной функциих
у = а , основание а>1
У
а >1
Область определения функции:
все действительные числа.
Множество значений функции:
все положительные числа.
Функция – возрастающая.
Функция не является ни четной,
ни нечетной.
Экстремумов нет
Наиб. и наим. значений нет
Ограничена снизу осью ох
Выпукла вниз
1
0
Х
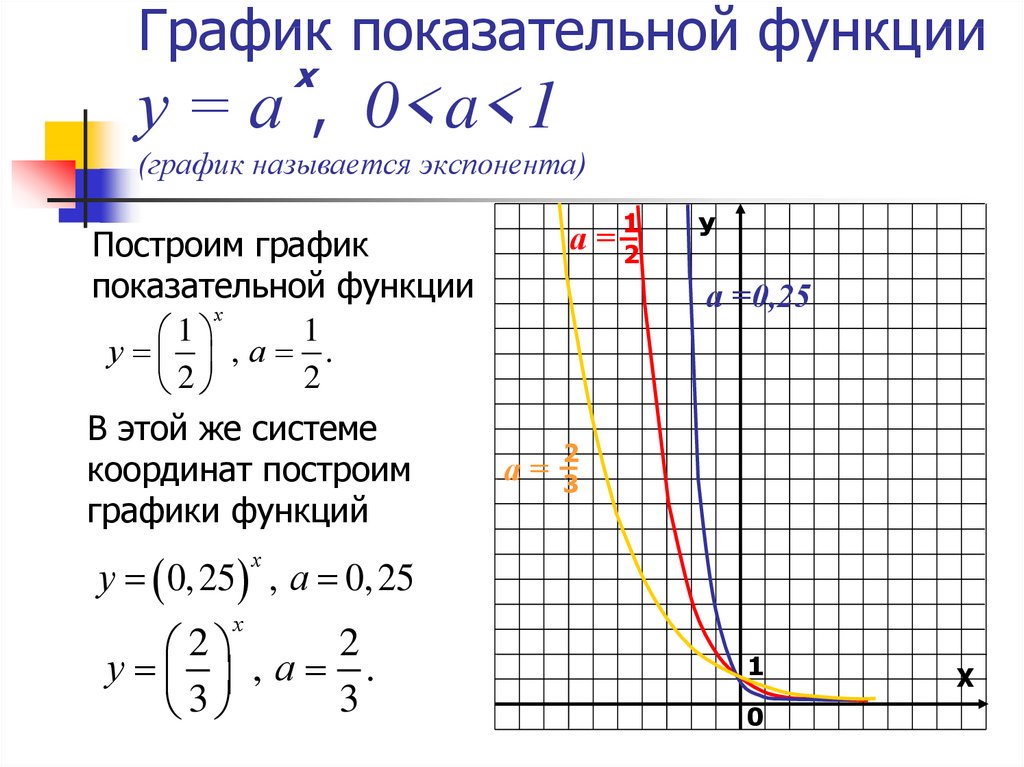
5. График показательной функции у = а , 0<a<1 (график называется экспонента)
График показательной функциих
у = а , 0<a<1
(график называется экспонента)
1
а=2
Построим график
показательной функции
х
1
1
у , а .
2
2
В этой же системе
координат построим
графики функций
У
а =0,25
а=
2
3
у 0, 25 , а 0, 25
х
х
2
2
у , а .
3
3
1
0
Х
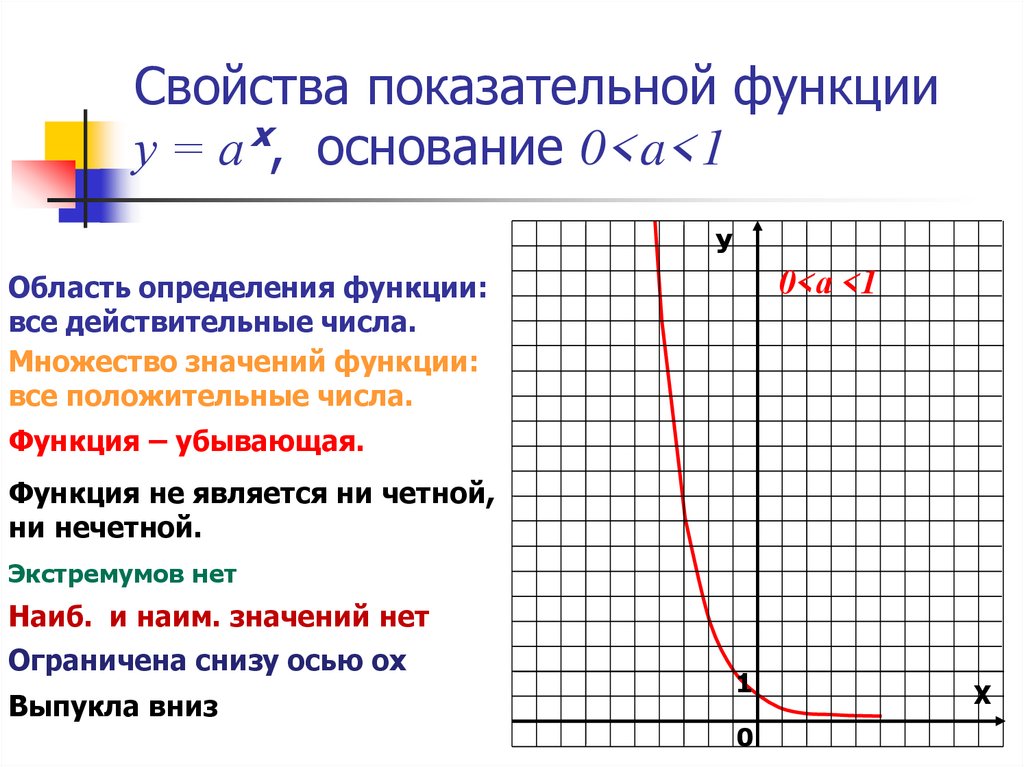
6. Свойства показательной функции у = а , основание 0<a<1
Свойства показательной функциих
у = а , основание 0<a<1
У
Область определения функции:
все действительные числа.
Множество значений функции:
все положительные числа.
0<а <1
Функция – убывающая.
Функция не является ни четной,
ни нечетной.
Экстремумов нет
Наиб. и наим. значений нет
Ограничена снизу осью ох
Выпукла вниз
1
0
Х
7. Рассмотрим примеры использования свойств
8.
9.
10. Закон радиоактивного распада
Закон радиоактивногоСоставить конспект по теме
распада
(определение, примеры,
графики, свойства,
рассмотренные упражнения)
Выполнить задание
Работу выслать до 21-00
14.05.2020







 Математика
Математика








