Похожие презентации:
Функциональные элементы цифровой электроники
1. Функциональные элементы цифровой электроники
Курс «Электроника и информационно-измерительная техника»Лектор: Зализный Д.И.
Тема 11
Функциональные элементы
цифровой электроники
2.
Логические уровни при напряжении питания +5 ВU, В
5
Логическая единица
2,4
Неопределённость
0,8
0
Логический ноль
t
3. Двоичный и шестнадцатеричный коды
4.
Целые двоичные числа без знака5.
Соотношение между десятичным кодом и двоичным кодомN DEC
n 1
Zi 2
i
i 0
Zi {0;1}
n – разрядность двоичного кода
i – номер разряда двоичного кода
6.
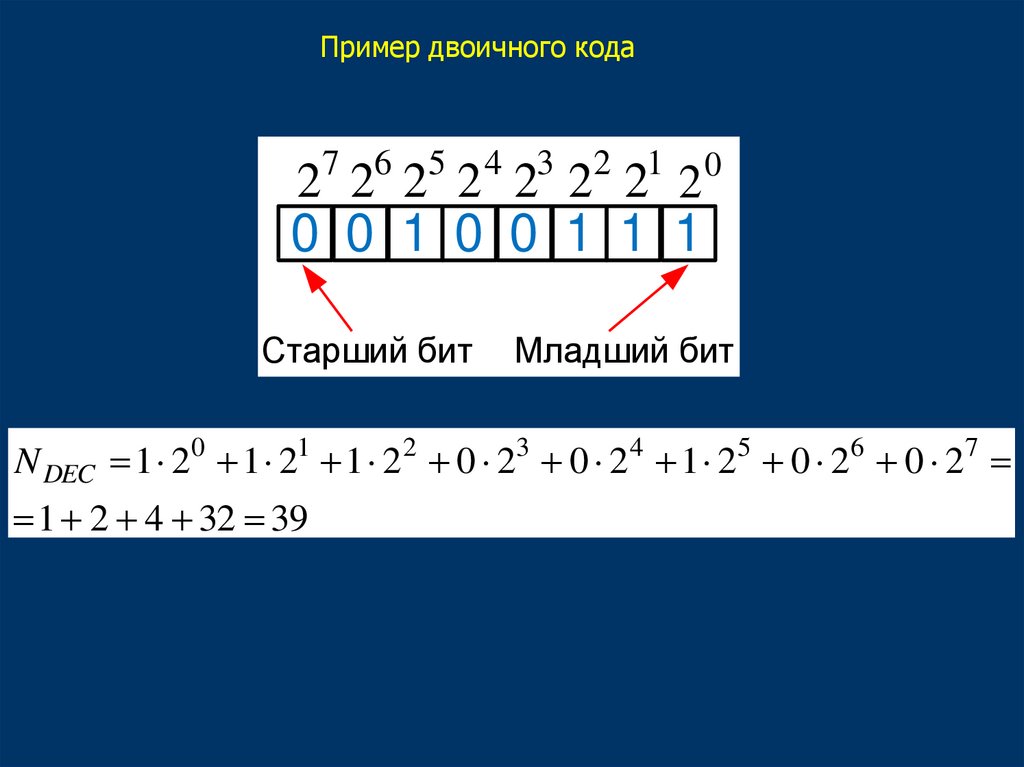
Пример двоичного кода7 6
5
4 3
2 1
2 2 2 2 2 2 2 20
0 0 1 0 0 1 1 1
Старший бит
Младший бит
N DEC 1 20 1 21 1 2 2 0 23 0 2 4 1 25 0 26 0 27
1 2 4 32 39
7.
Единицы измерения информации в двоичных кодах1 Байт = 8 бит
1К Байт (кибибайт) =210 Байт = 1024 байт
1M Байт (мебибайт) =220 Байт = 1048576 байт
1Г Байт (гибибайт) =230 Байт = 1073741824 байт
1Т (тебибайт) Байт =240 Байт = 1099511627760 байт
8.
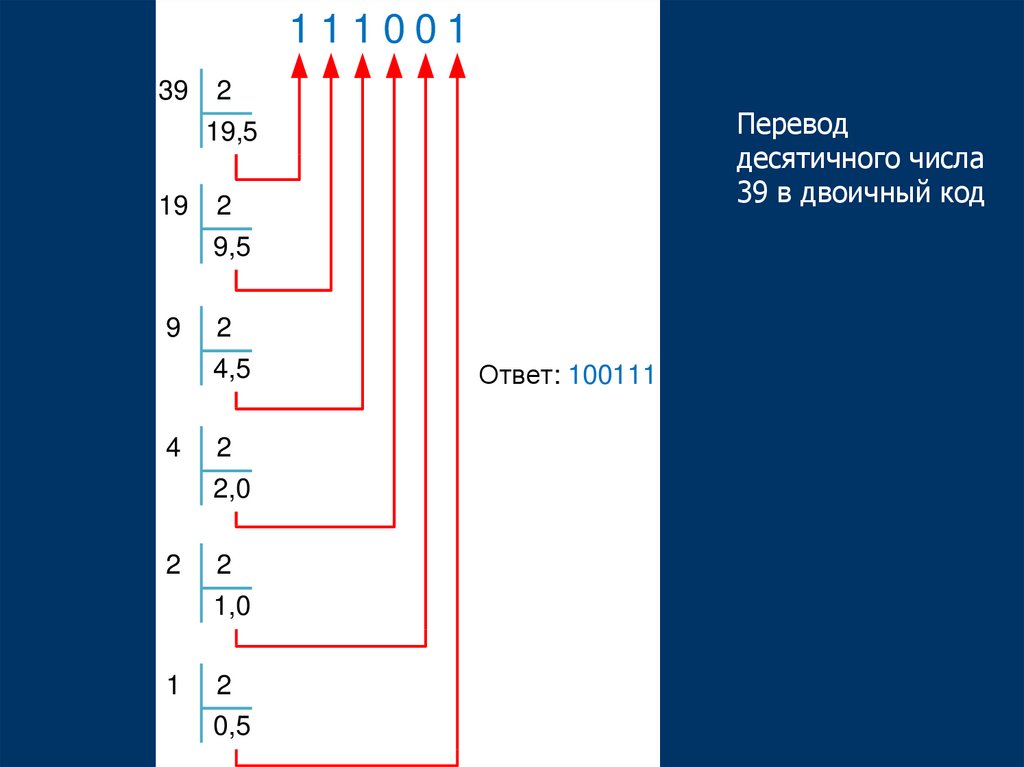
11100139
2
Перевод
десятичного числа
39 в двоичный код
19,5
19
2
9,5
9
2
4,5
4
2
2,0
2
2
1,0
1
2
0,5
Ответ: 100111
9.
Целые двоичные числа со знаком10.
Пример: +70 0 0 0 0 1 1 1
Бит знака
11.
Пример: -71 1 1 1 1 0 0 1
Целая часть
в дополнительном коде
Перевод целой части в дополнительный код:
0000111
инверсия
1111000
0000001
1111001
прибавление единицы
12.
Двоичные числа с фиксированной запятой (точкой)(fixed point)
13.
Пример2 1
2 2 2
0
1
2 3 4
2 2 2 2
0 0 1 0 ,0 1 1 1
Бит знака
Целая часть Дробная часть
Перевод из двоичного кода в десятичный
N DEC 0 22 1 21 0 20 0 2 1 1 2 2 1 2 3 1 2 4
2 0,25 0,125 0,0625 2,4375.
14.
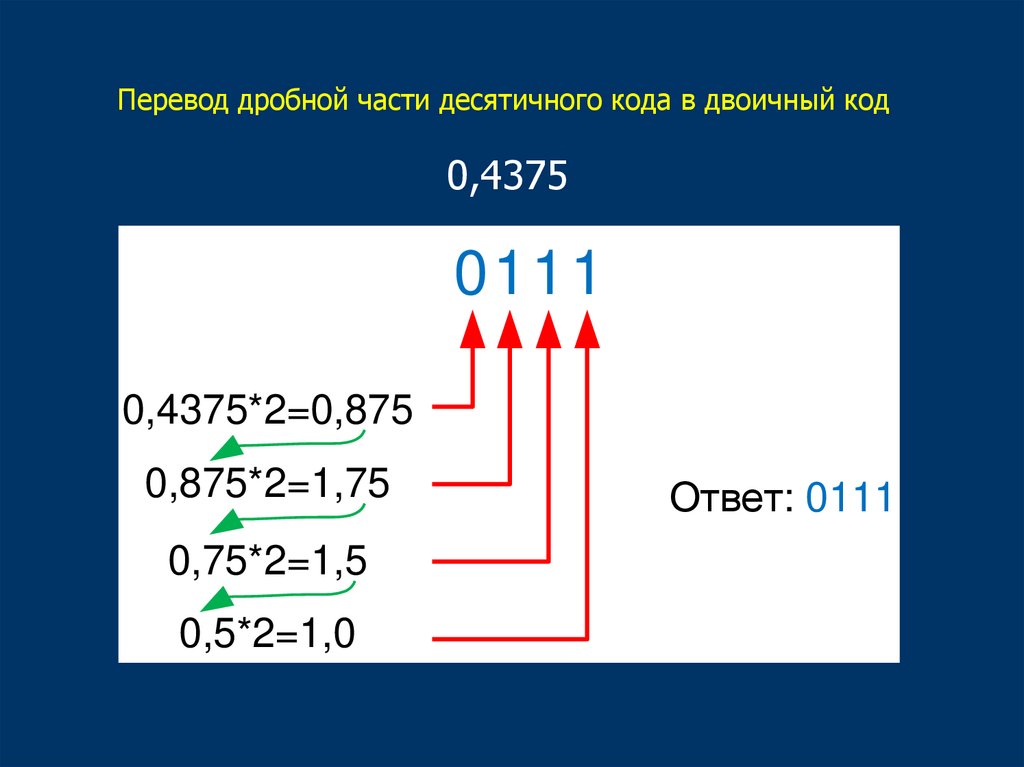
Перевод дробной части десятичного кода в двоичный код0,4375
0111
0,4375*2=0,875
0,875*2=1,75
0,75*2=1,5
0,5*2=1,0
Ответ: 0111
15.
Двоичные числа плавающей запятой (точкой)(floating point)
16.
Стандарт IEEE 754-2008IEEE - Institute of Electrical and Electronics Engineers
Числа одинарной точности
(4 байта памяти на 1 число)
N 1 2
S
от
3,4 10 38
E 127
до
M
1 23
2
3,4 1038
Числа двойной точности
(8 байт памяти на 1 число)
N 1
S
от
M
E 1023
2
1
1,7 10 308
S - бит знака
E - смещённый показатель степени
М - мантисса (основание) числа
до
2
52
1,7 10308
17.
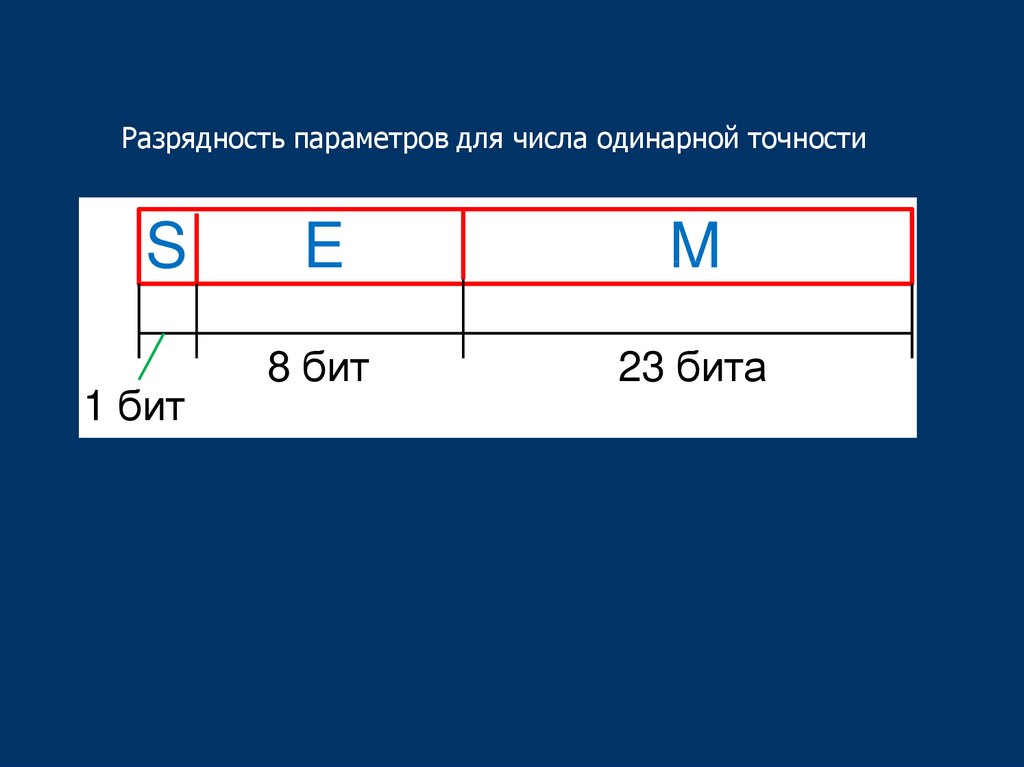
Разрядность параметров для числа одинарной точностиS
1 бит
E
M
8 бит
23 бита
18.
Пример представления числа 2,4375 в формате с плавающейзапятой одинарной точности
1. Запись в формате с фиксированной запятой
2,4375 DEC 010,0111 BIN
2. Нормализация числа (сдвиг запятой) до значения мантиссы от 1 до 2
128 127
010,0111BIN 01,00111BIN 2 01,00111BIN 2
1
3. Запись мантиссы без учёта единицы в целой части
M BIN 0011100000.....0....
19.
4. Бит знакаS 0
5. Показатель степени
E 128DEC 10000000 BIN
Ответ
Число 2,4375
01000000000111000000000000000000
20.
Шестнадцатеричный код(hexadecimal - HEX)
21.
Таблица соответствий цифрDEC 0 1 2 3 4 5 6
7 8 9
10
11
12
13
14
15
HEX 0 1 2 3 4 5 6
7 8 9
A
B
C
D
E
F
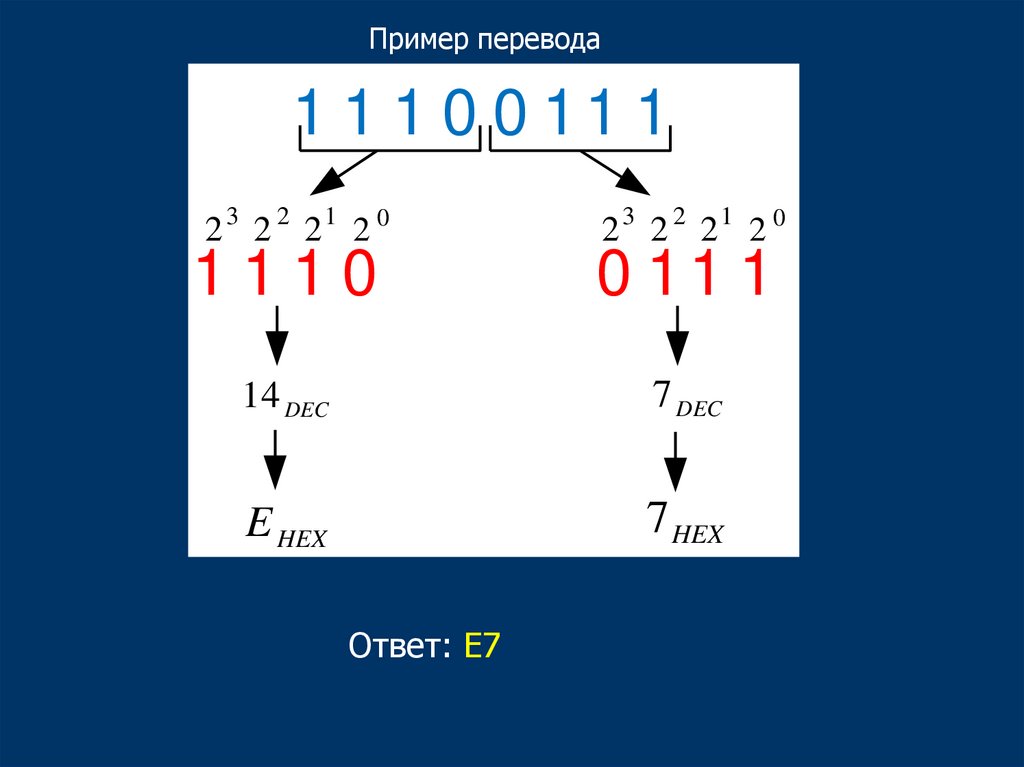
22.
Пример перевода1 1 1 0 0 11 1
2 3 2 2 21 2 0
2 3 2 2 21 2 0
1110
0 11 1
14 DEC
7 DEC
E HEX
7 HEX
Ответ: Е7
23. Простейшие арифметические операции с двоичными числами без знака
24.
Правила арифметического сложения двоичных чисел0+0=0
0+1=1
1+0=1
1 + 1 = 10
1 + 1 + 1 = 11
25.
Пример арифметического сложения двоичных чисел1 11 1
11 1
1 11
0 1 1 1 0
+0 1 1 1 1
1
1
0
1
1
0
1 11 1 1 00 00 1 1
26.
Правила арифметического вычитания двоичных чиселABIN BBIN ABIN BBIN.доп ABIN BBIN 1
где: BBIN .доп - число BBIN в дополнительном коде; BBIN проинвертированное число BBIN .
Если A B , то результат получается в прямом коде. При этом в старшем
разряде появляется единица (перенос), которую в результате учитывать
не нужно. Если A B , то результат получается в дополнительном коде.
Для перехода в прямой код его нужно проинвертировать, а затем
прибавить единицу.
27.
Пример вычитания №1:ABIN 1111 ; BBIN 0110 .
BBIN 1001.
BBIN .доп 1001 0001 1010 .
ABIN BBIN ABIN BBIN .доп 1111 1010 11001
Ответ: 1001BIN . (15-6=9).
Перенос в старший разряд
не учитываем
28.
Пример вычитания №2:ABIN 0110 ; BBIN 1111 .
BBIN 0000 .
BBIN .доп 0000 0001 0001 .
ABIN BBIN ABIN BBIN .доп 0110 0001 0111 .
0111 1000 .
1000 0001 1001 .
Ответ: 0111BIN .доп 1001BIN . (6-15=-9).
29.
Пример умножения двоичных чисел7х6
0111
0110
0000
01110
011100
0000000
0101010
сдвиг влево
30. Логические операции в цифровой электронике
31.
Логические операции в цифровой электроникеИнверсия
(логическое отрицание)
Конъюнкция
(логическое умножение)
Дизъюнкция
(логическое сложение)
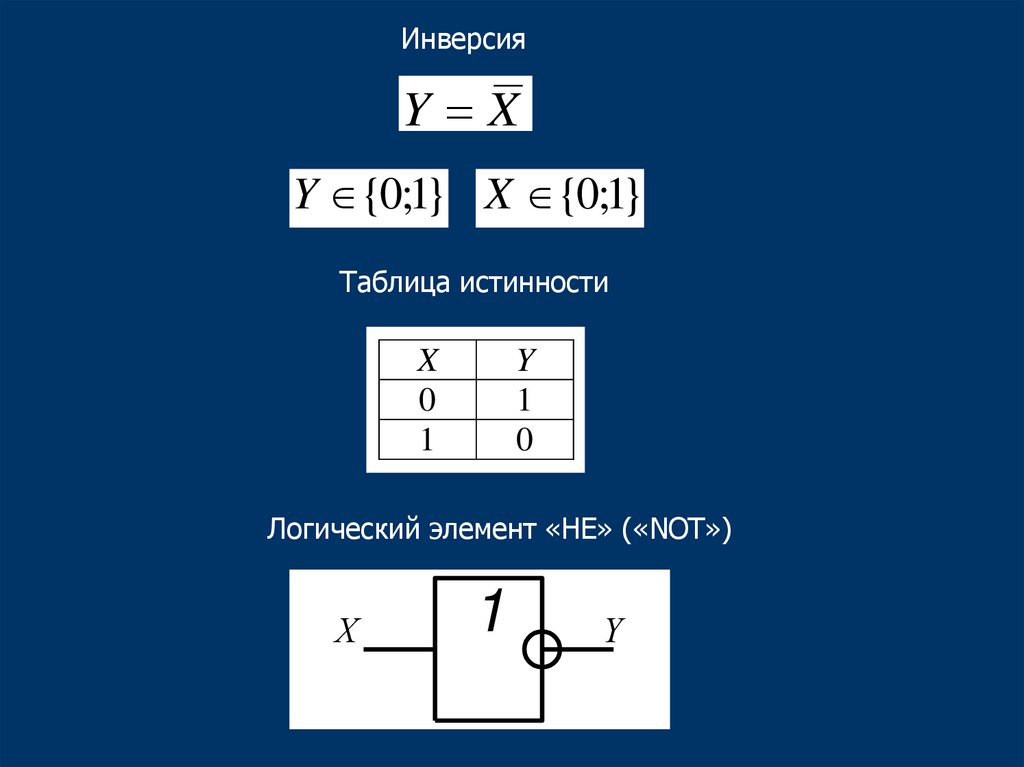
32.
ИнверсияY X
Y {0;1} X {0;1}
Таблица истинности
X
0
1
Y
1
0
Логический элемент «НЕ» («NOT»)
X
1
Y
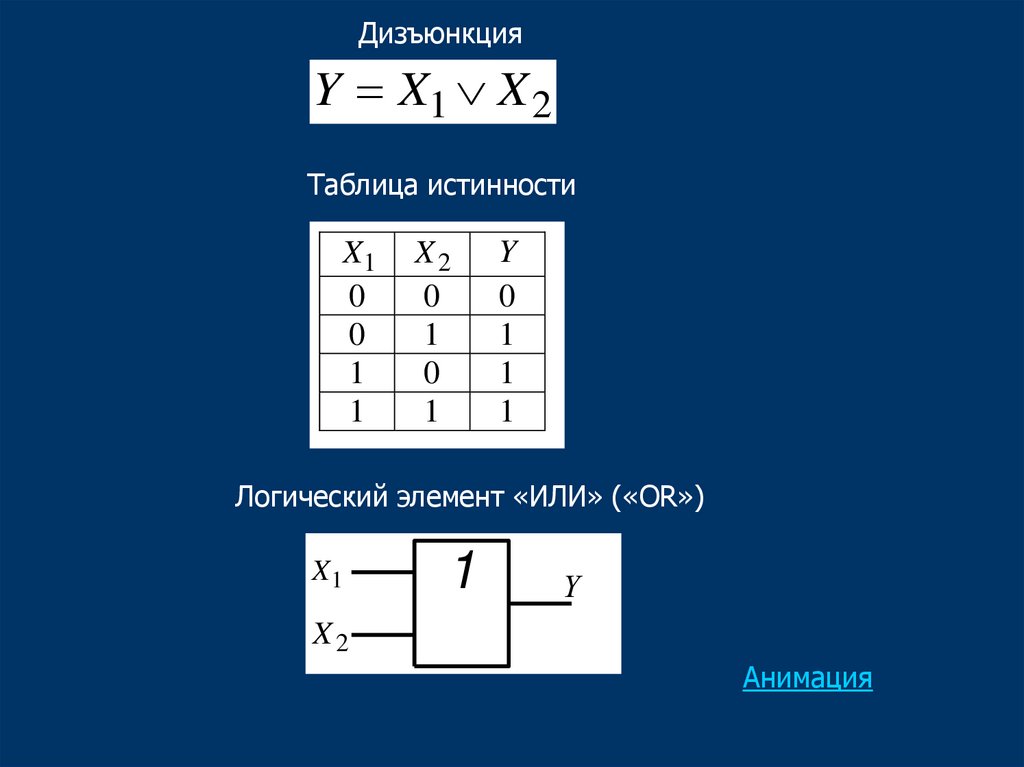
33.
ДизъюнкцияY X1 X 2
Таблица истинности
X1
0
0
1
1
X2
0
1
0
1
Y
0
1
1
1
Логический элемент «ИЛИ» («OR»)
X1
1
Y
X2
Анимация
34.
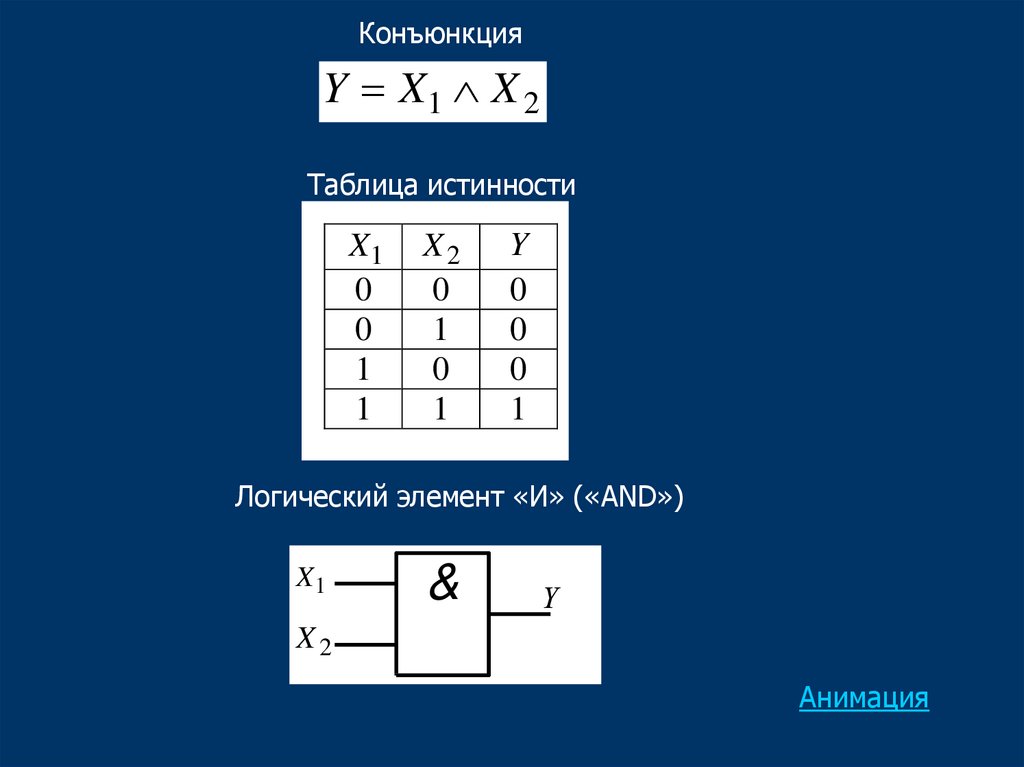
КонъюнкцияY X1 X 2
Таблица истинности
X1
0
0
1
1
X2
0
1
0
1
Y
0
0
0
1
Логический элемент «И» («AND»)
X1
&
Y
X2
Анимация
35.
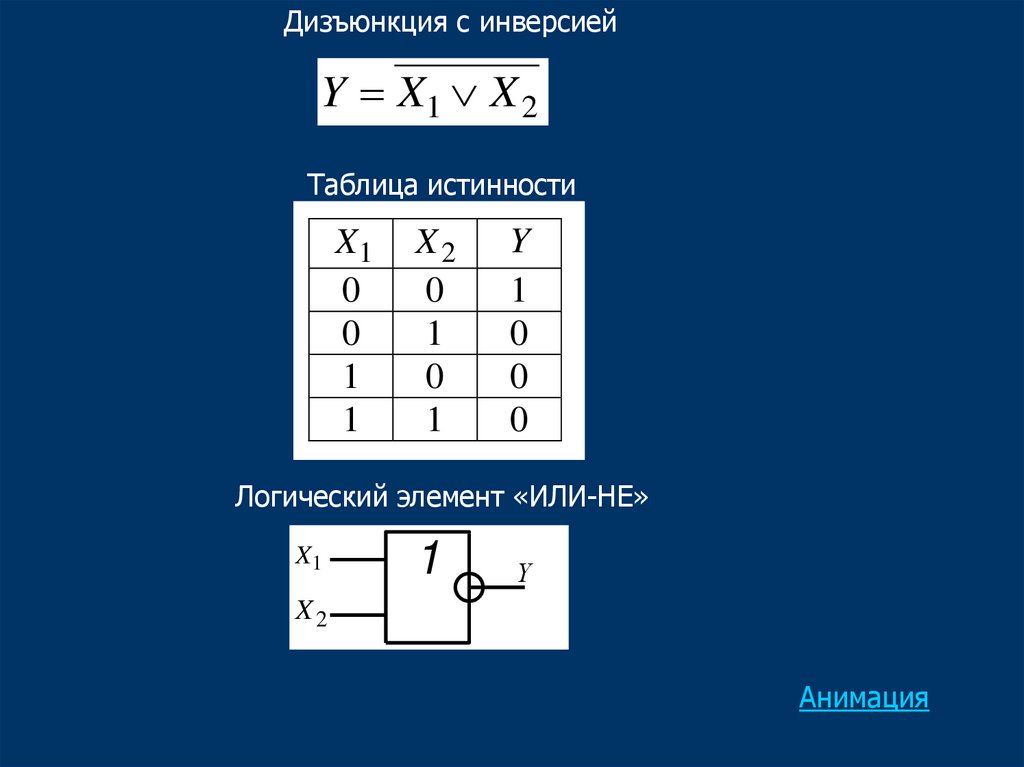
Дизъюнкция с инверсиейY X1 X 2
Таблица истинности
X1
0
0
1
1
X2
0
1
0
1
Y
1
0
0
0
Логический элемент «ИЛИ-НЕ»
X1
1
Y
X2
Анимация
36.
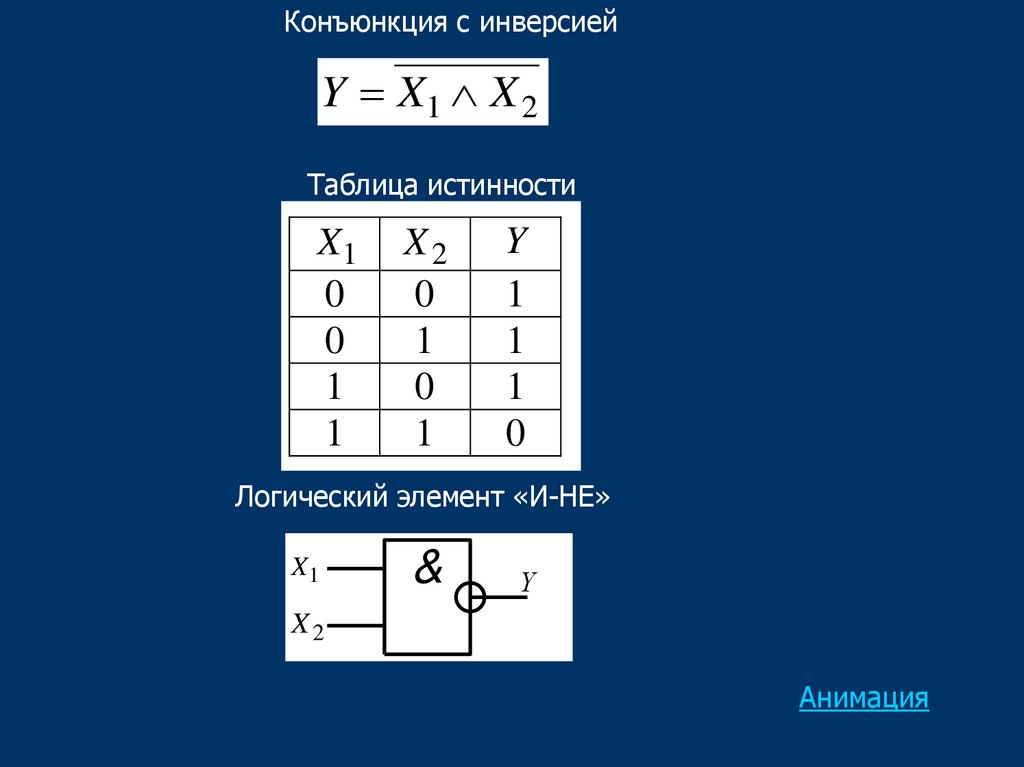
Конъюнкция с инверсиейY X1 X 2
Таблица истинности
X1
0
0
1
1
X2
0
1
0
1
Y
1
1
1
0
Логический элемент «И-НЕ»
X1
&
Y
X2
Анимация
37.
Микросхема КP1533ЛА3 (IN74HC00)38. Цифровые триггеры
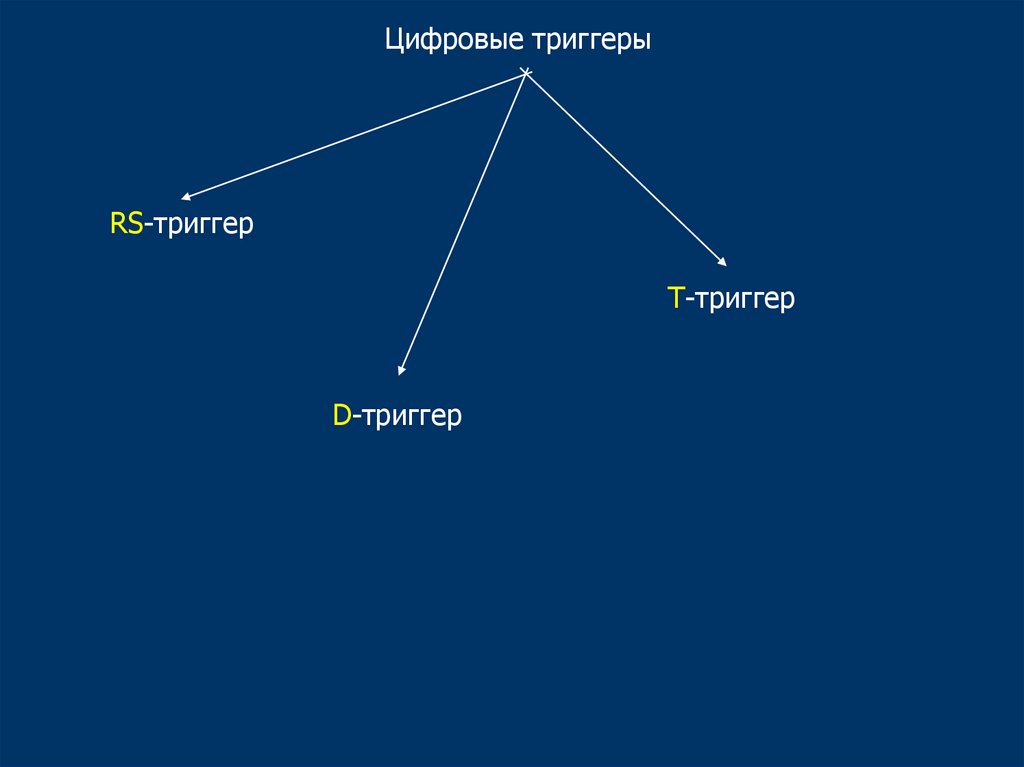
39.
Цифровые триггерыRS-триггер
Т-триггер
D-триггер
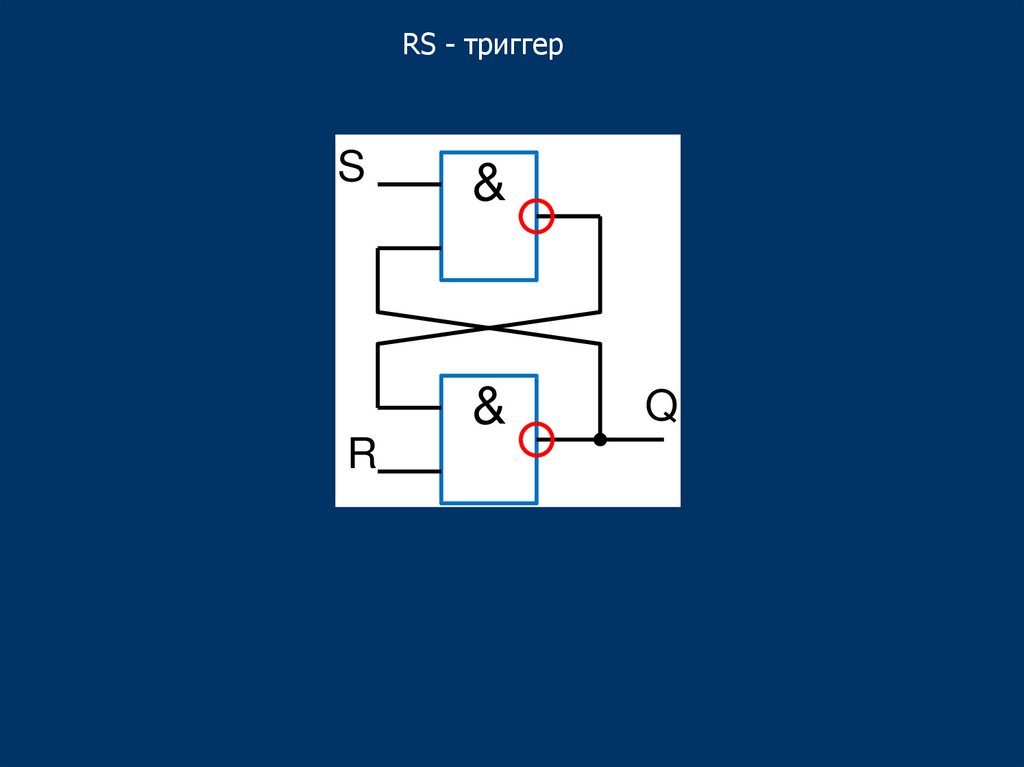
40.
RS - триггерS
&
&
R
Q
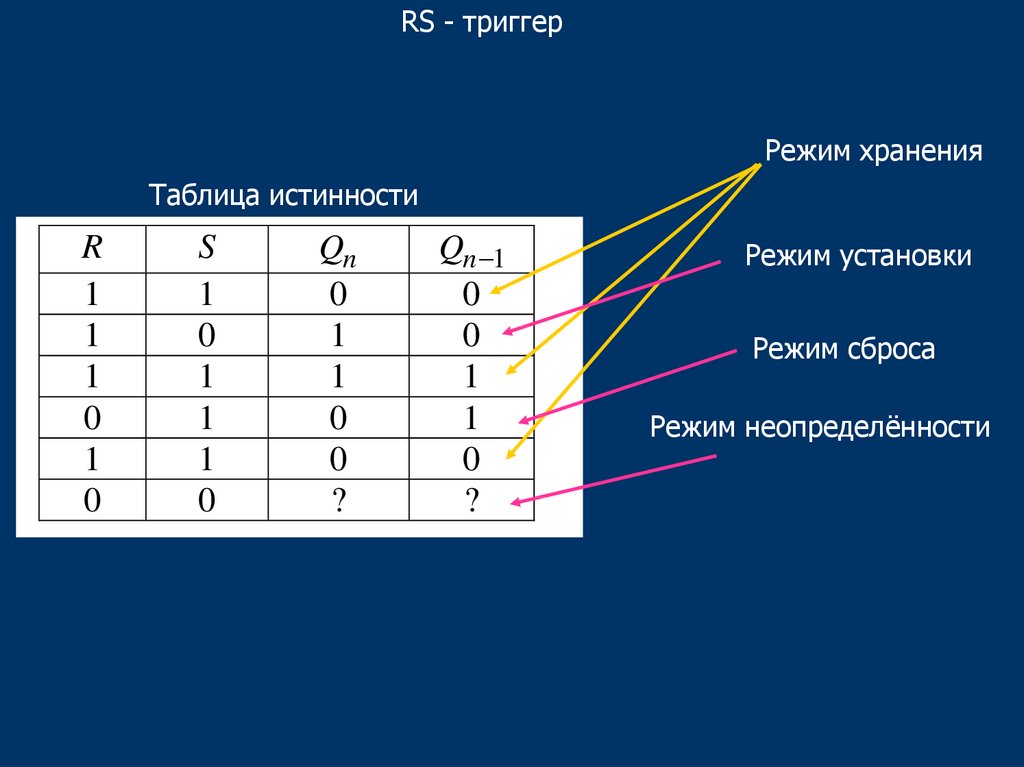
41.
RS - триггерРежим хранения
Таблица истинности
R
1
1
1
0
1
0
S
1
0
1
1
1
0
Qn
0
1
1
0
0
?
Qn 1
0
0
1
1
0
?
Режим установки
Режим сброса
Режим неопределённости
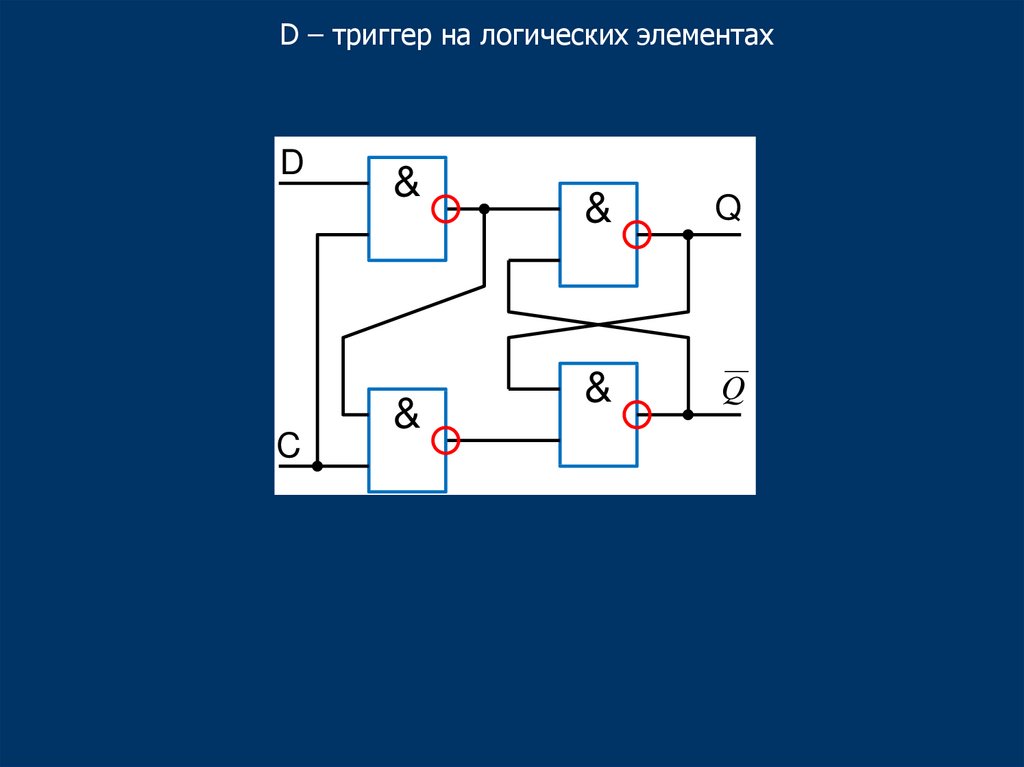
42.
D – триггер на логических элементахD
C
&
&
&
Q
&
Q
43.
D - триггерD T
Q
Q
C
D
t
C
t
Q
t
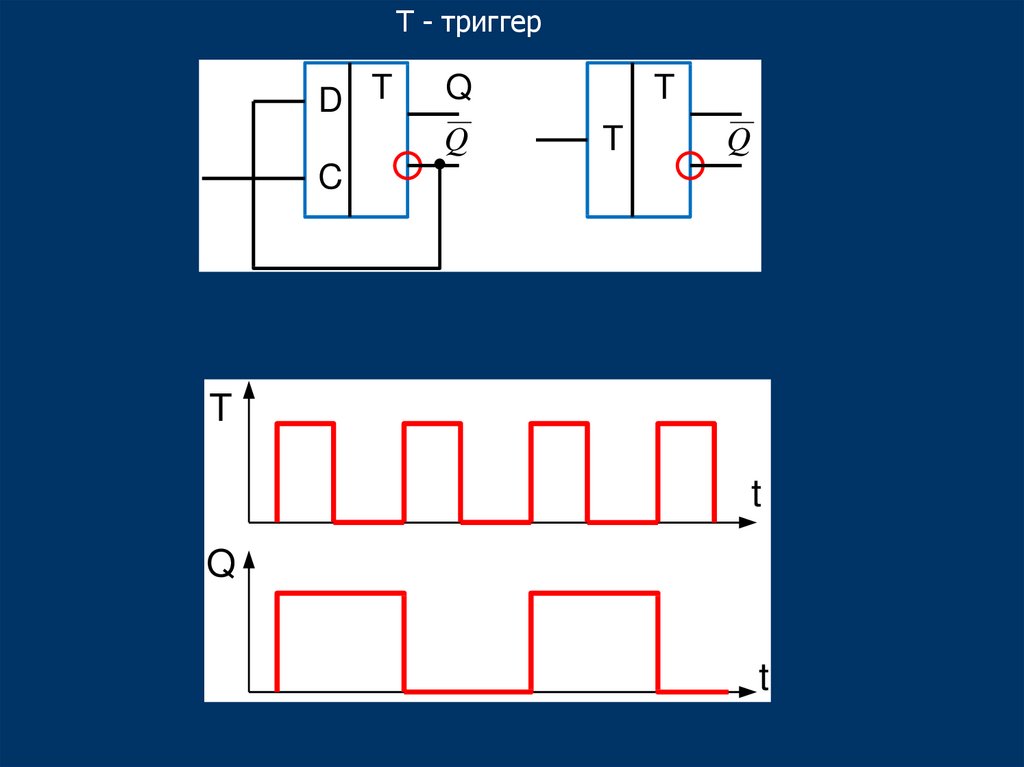
44.
T - триггерD T
Q
Q
T
T
Q
C
T
t
Q
t
45. Двоичные счётчики
46.
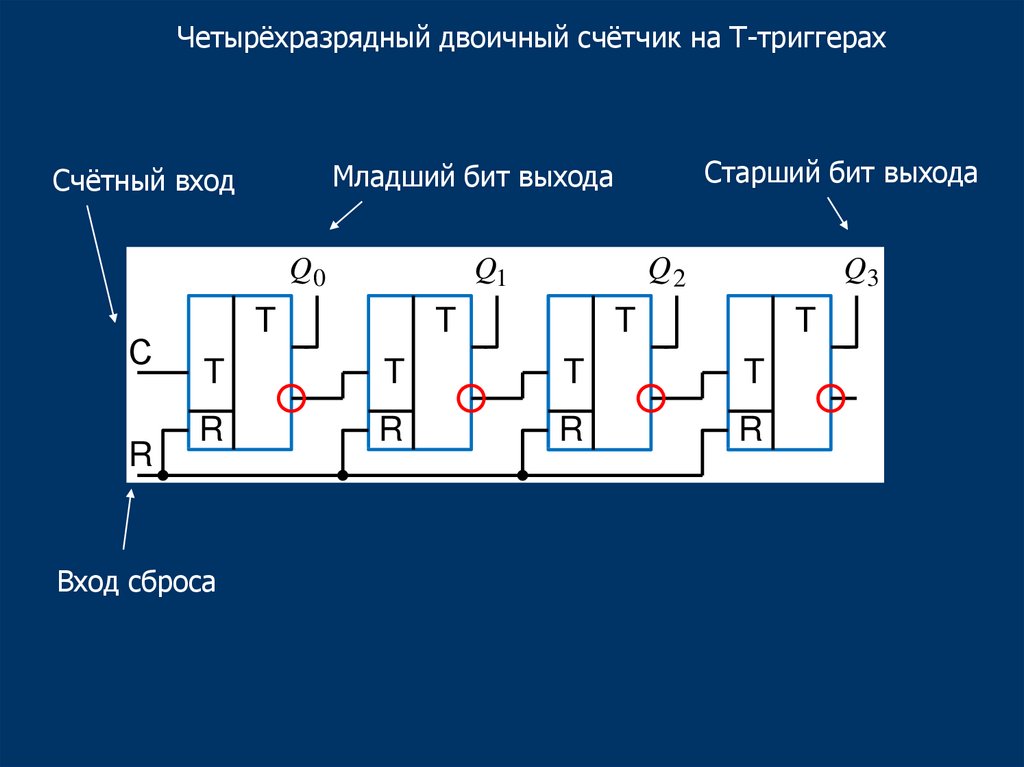
Четырёхразрядный двоичный счётчик на Т-триггерахQ0
С
R
Старший бит выхода
Младший бит выхода
Счётный вход
Q2
Q1
T
T
Q3
T
T
T
T
T
T
R
R
R
R
Вход сброса
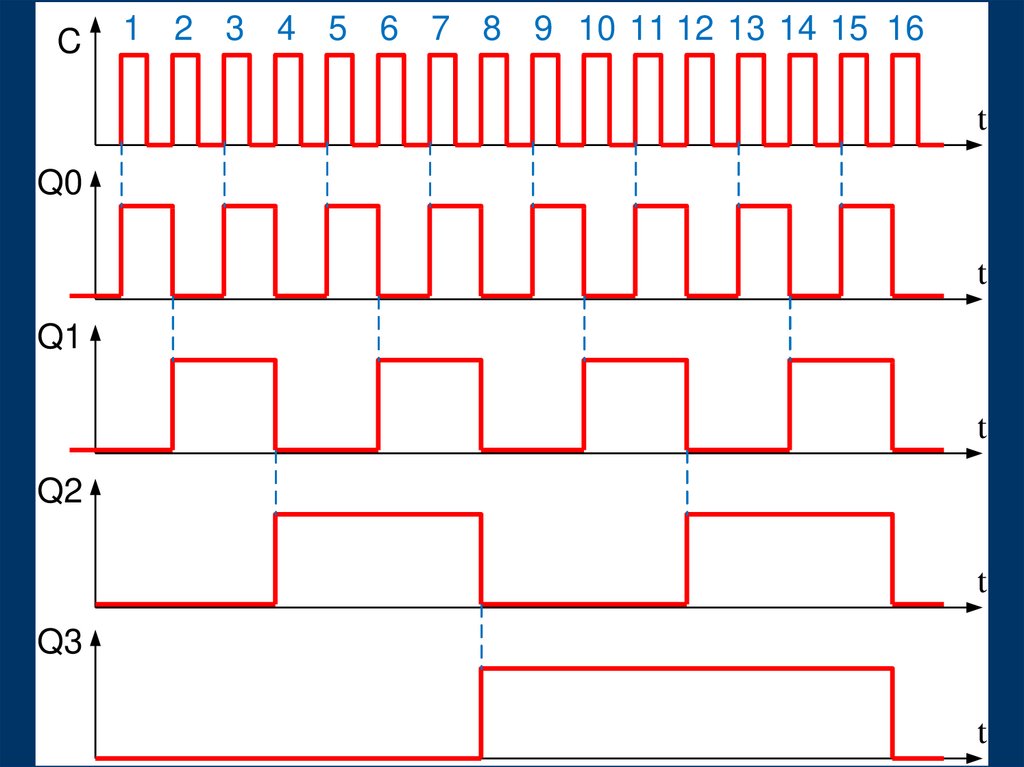
47.
C1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
t
Q0
t
Q1
t
Q2
t
Q3
t
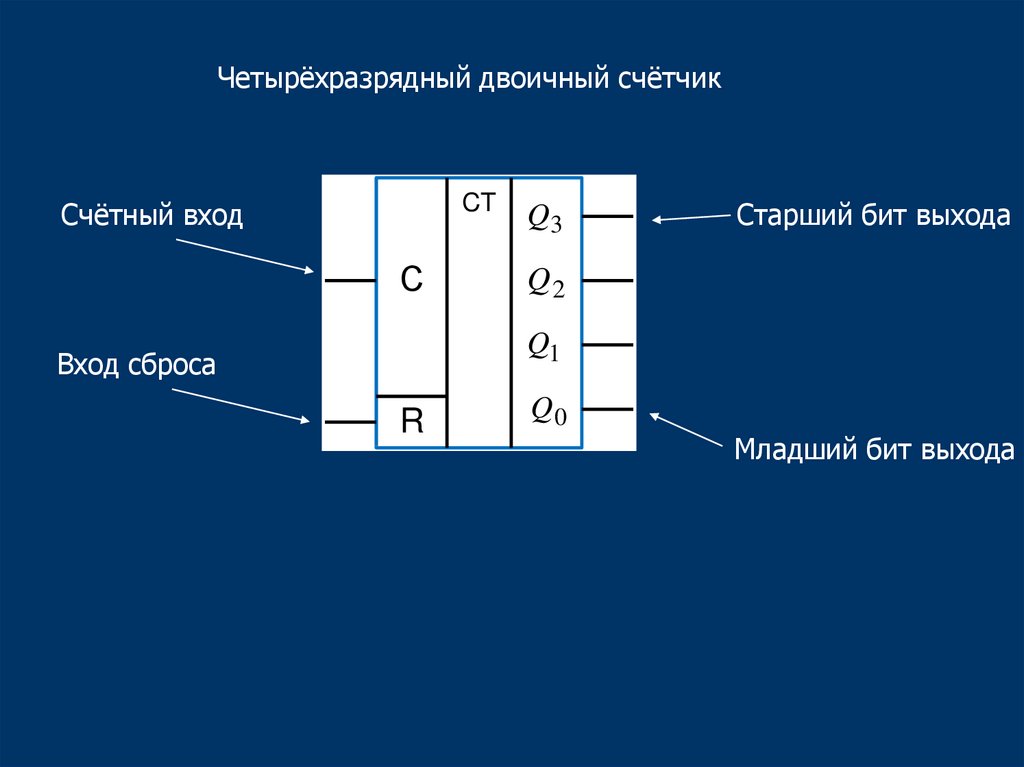
48.
Четырёхразрядный двоичный счётчикCT
Счётный вход
С
Q3
Старший бит выхода
Q2
Q1
Вход сброса
R
Q0
Младший бит выхода
49.
Таблица истинности четырехразрядного двоичного счетчикаN имп 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0
Q0
0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0
Q1
0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 0
Q2
0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 0
Q3
Анимация
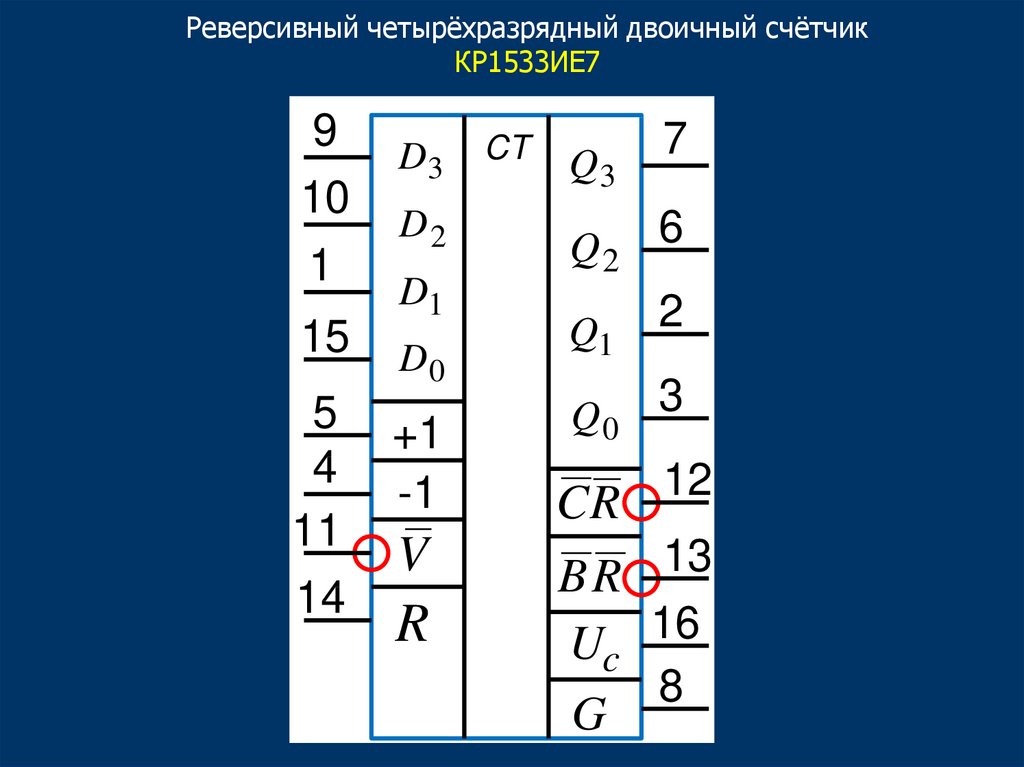
50.
Реверсивный четырёхразрядный двоичный счётчикКР1533ИЕ7
9
10
1
15
D3
D2
D1
D0
5
4
11
+1
-1
14
R
V
CT
Q3
Q2
Q1
7
6
2
Q0 3
12
CR
B R 13
Uc 16
8
G
51. Цифровые регистры
52.
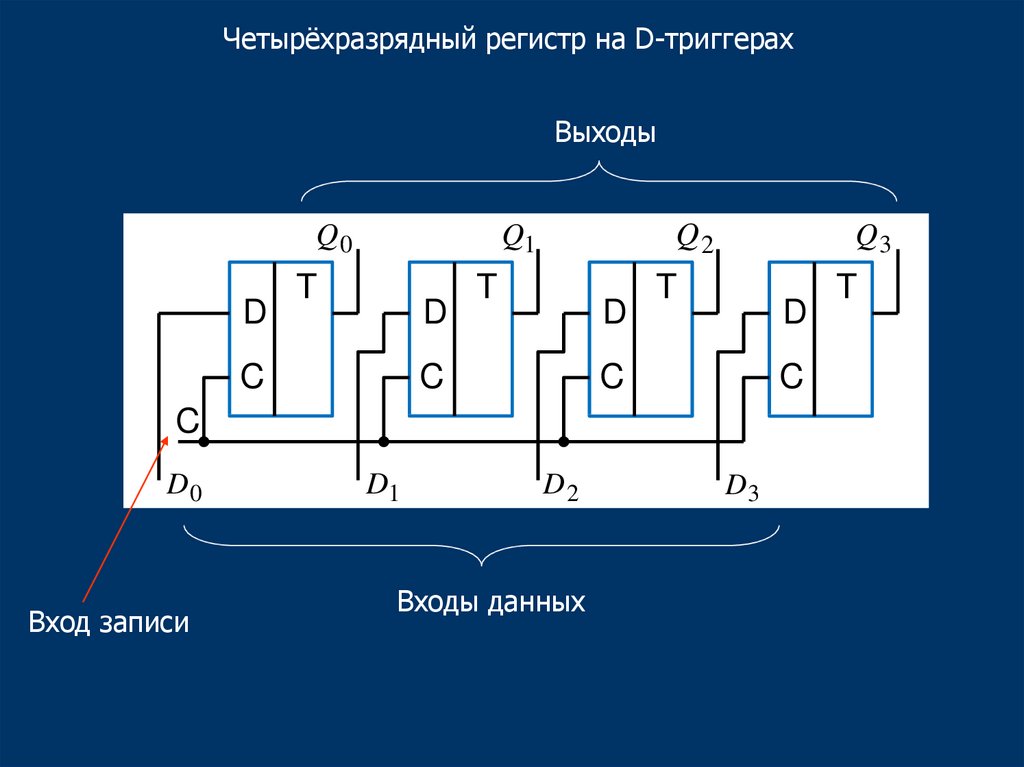
Четырёхразрядный регистр на D-триггерахВыходы
Q0
D
Q2
Q1
T
D
C
T
D
C
Q3
T
D
C
C
C
D0
Вход записи
D1
D2
Входы данных
D3
T
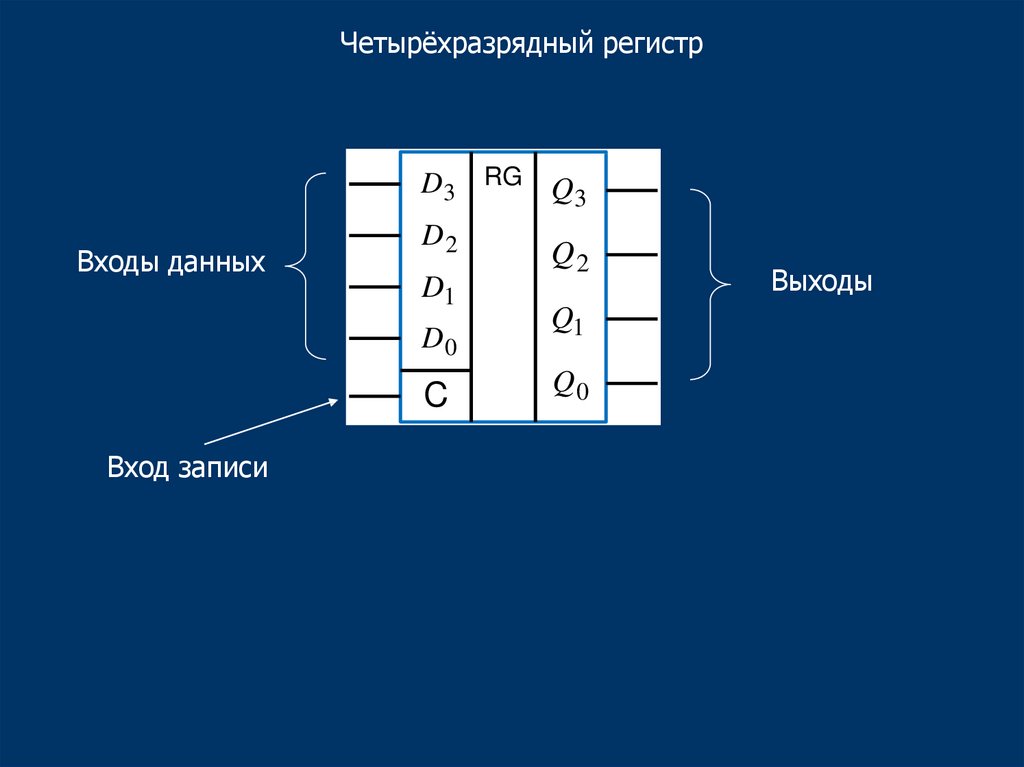
53.
Четырёхразрядный регистрВходы данных
D3 RG Q3
D2
D1
D0
C
Вход записи
Q2
Q1
Q0
Выходы
54. Цифровые мультиплексоры
55.
Четырёхразрядный мультиплексорD3 MUX
Входы данных
D2
D1
D0
Входы адреса
А1
А0
Q
Выход
56.
Таблица истинности мультиплексораA1
A2
Q
0
0
D0
0
1
D1
1
0
D2
1
1
D3


































 Электроника
Электроника








