Цифровая схемотехника

1. Курс лекций по дисциплине «Цифровая схемотехника»

2. Системы счисления

Изначально число – способ выражения количества
предметов или количественного отношения между
предметами
Можно придумать разные способы изображения
(хранения) числа. Значение числа от способа его
изображения не зависит
Системы счисления бывают:
– непозиционная;
–позиционная.

3. Системы счисления

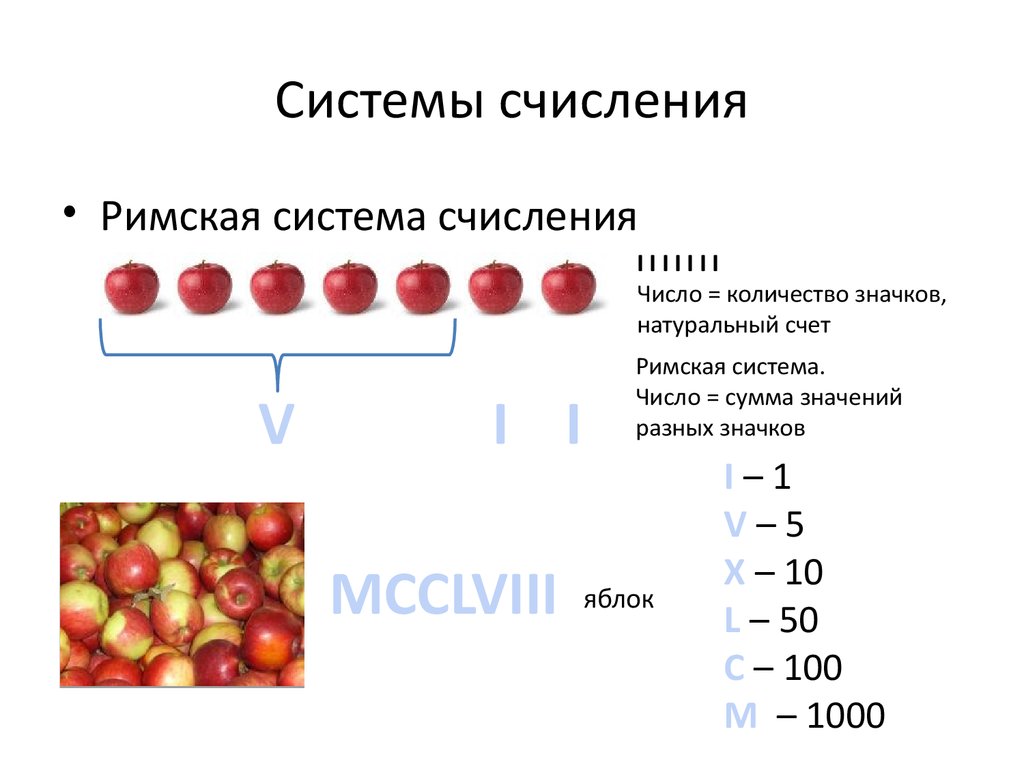
• Римская система счисления
IIIIIII
Число = количество значков,
натуральный счет
V
I I
MCCLVIII
Римская система.
Число = сумма значений
разных значков
яблок
I–1
V–5
X – 10
L – 50
C – 100
M – 1000

4. Системы счисления

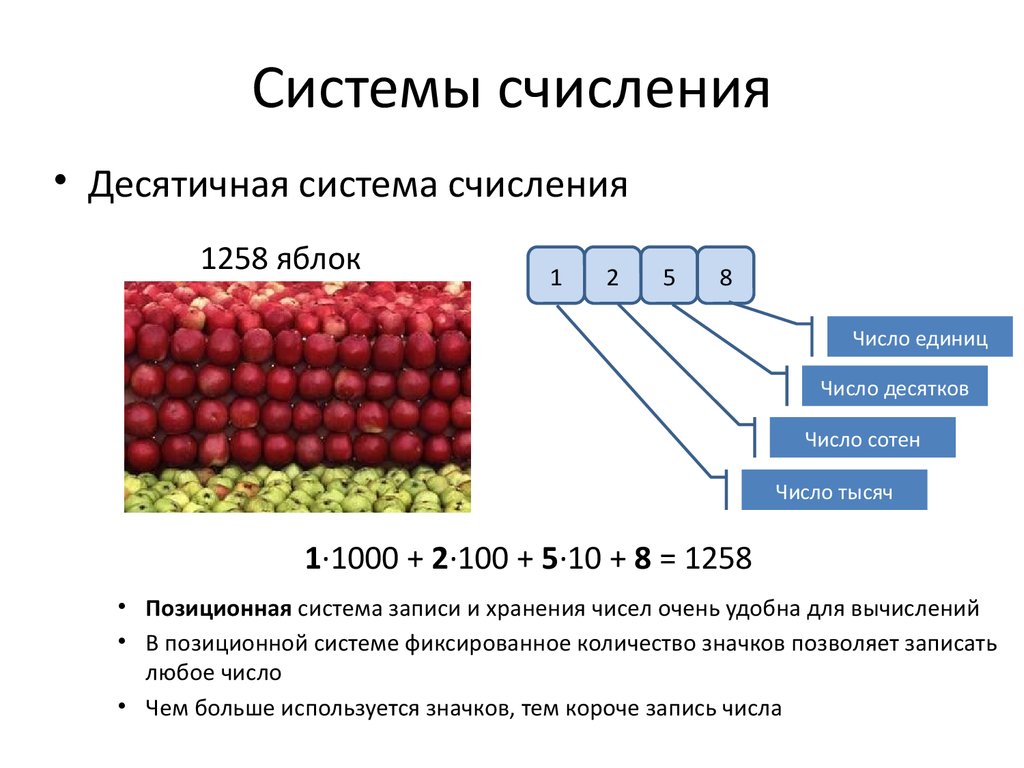
• Десятичная система счисления
1258 яблок
1
2
5
8
Число единиц
Число десятков
Число сотен
Число тысяч
1∙1000 + 2∙100 + 5∙10 + 8 = 1258
• Позиционная система записи и хранения чисел очень удобна для вычислений
• В позиционной системе фиксированное количество значков позволяет записать
любое число
• Чем больше используется значков, тем короче запись числа

5. Системы счисления

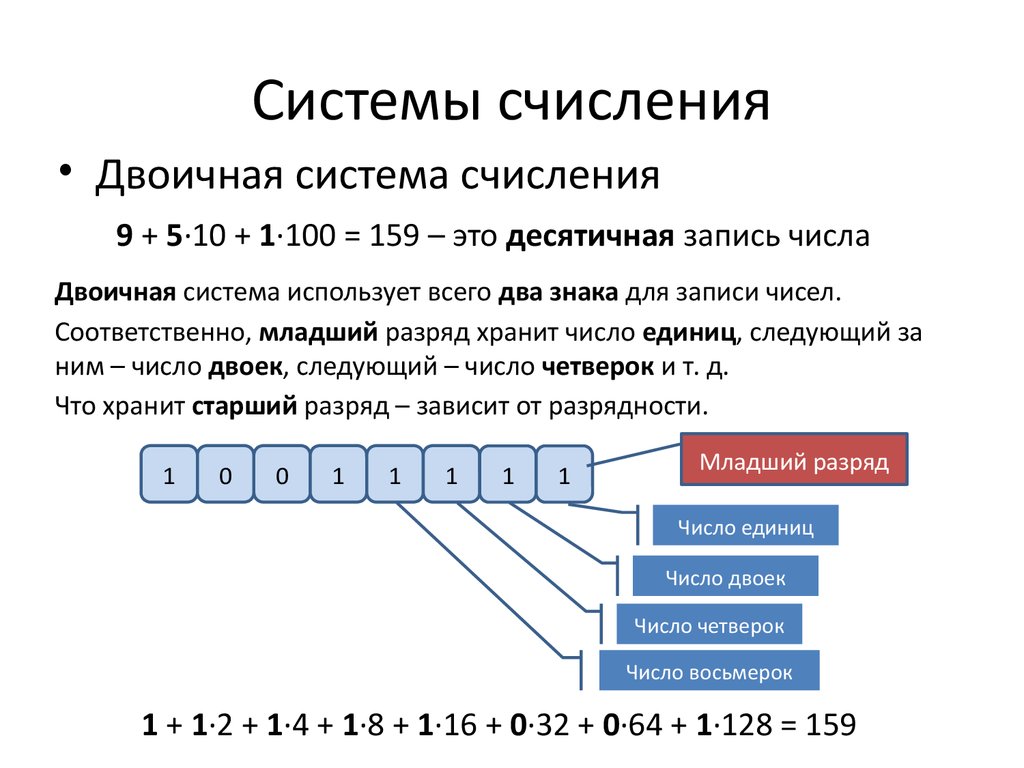
• Двоичная система счисления
9 + 5∙10 + 1∙100 = 159 – это десятичная запись числа
Двоичная система использует всего два знака для записи чисел.
Соответственно, младший разряд хранит число единиц, следующий за
ним – число двоек, следующий – число четверок и т. д.
Что хранит старший разряд – зависит от разрядности.
1
0
0
1
1
1
1
1
Младший разряд
Число единиц
Число двоек
Число четверок
Число восьмерок
1 + 1∙2 + 1∙4 + 1∙8 + 1∙16 + 0∙32 + 0∙64 + 1∙128 = 159

6. Системы счисления

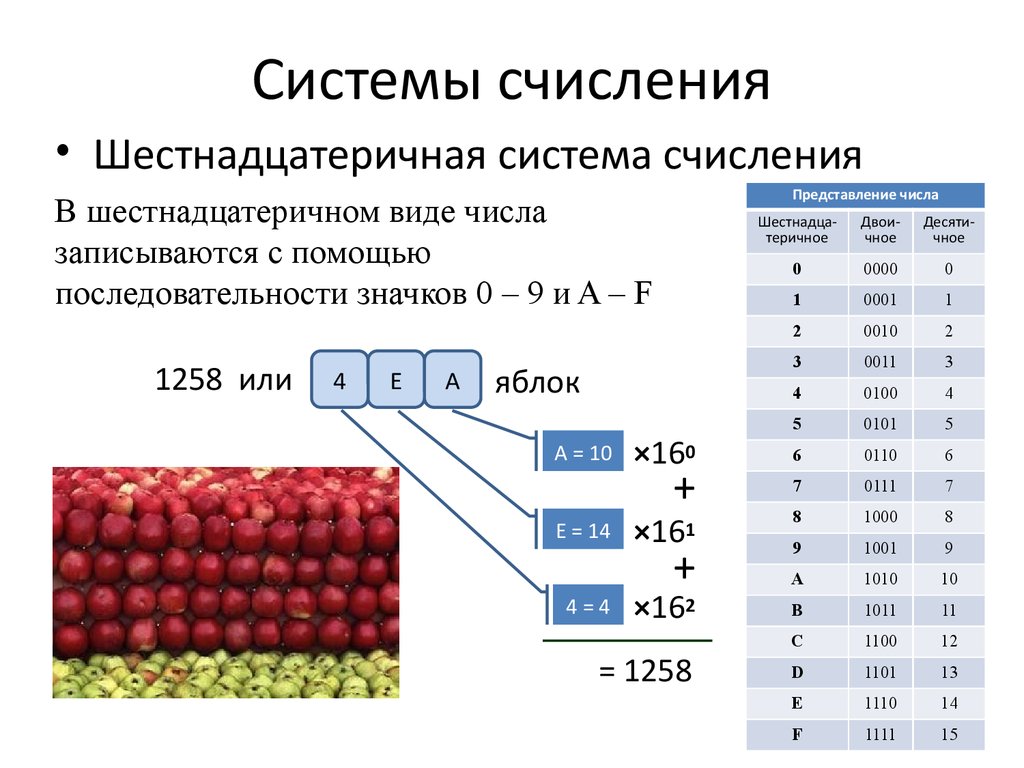
• Шестнадцатеричная система счисления
Представление числа
В шестнадцатеричном виде числа
записываются с помощью
последовательности значков 0 – 9 и A – F
1258 или
4
E
A
яблок
A = 10
E = 14
4=4
×160
+
×16
1
+
×162
= 1258
Шестнадцатеричное
Двоичное
Десятичное
0
0000
0
1
0001
1
2
0010
2
3
0011
3
4
0100
4
5
0101
5
6
0110
6
7
0111
7
8
1000
8
9
1001
9
A
1010
10
B
1011
11
C
1100
12
D
1101
13
E
1110
14
F
1111
15

7. Системы счисления

Перевод чисел из двоичной системы в
шестнадцатеричную и наоборот
• Для перевода многозначного двоичного числа в
шестнадцатеричную систему нужно разбить его на
тетрады справа налево и заменить каждую тетраду
соответствующей шестнадцатеричной цифрой.
• Для перевода числа из шестнадцатеричной
системы в двоичную нужно заменить каждую его
цифру на соответствующую тетраду двоичной
системы.
Например: 0101101000112 = 0101 1010 0011 = 5A316

8. Логические устройства

Основные положения алгебры логики
Переменная величина Х в алгебре логики может
принимать: Х = 1 (логическая единица лог. «1»);
Х = 0 (логический ноль лог. «0»)
Три основных операции:
– инверсия (логическое отрицание);
– дизъюнкция (логическое сложение);
– конъюнкция (логическое умножение).

9. Инверсия (логическое отрицание)

•Операция инверсии на языке логики называется
«НЕ», «NOT».
Инвертированный сигнал X в алгебре логики
обозначается как .
Зависимость между логическими переменными
отображается таблицами истинности.
X
Y
0
1
1
0
На электрических схемах:
1

10. Дизъюнкция (логическое сложение)

•Операция дизъюнкции на языке логики
называется «ИЛИ», «OR»
Дизъюнкция сигналов Х1 и Х2 в алгебре логики
записывается как ;
X
X
Y
Таблица истинности
1
На электрических схемах:
2
0
0
0
0
1
1
1
0
1
1
1
1

11. Конъюнкция (логическое умножение)

•Операция конъюнкции на языке логики
называется «И», «AND».
Конъюнкция сигналов Х1 и Х2 в алгебре логики
записывается как ;
Таблица истинности
X
X
Y
1
На электрических схемах:
2
0
0
0
0
1
0
1
0
0
1
1
1

12. «Исключающее или»

•Операция «исключающее или» на языке логики
называется «XOR», «eXclusive OR»
XOR сигналов Х1 и Х2 в алгебре логики
записывается как ;
Таблица истинности
X
X
Y
1
2
0
0
0
0
1
1
1
0
1
1
1
0
На электрических схемах:

13. Основные соотношения , правила, теоремы

Х0=Х
Х1=1
ХХ=Х
Х=1
Дистрибутивный закон:
Закон поглощения:
Правило склеивания:
Правило двойного отрицания
Теорема де Моргана:
Х0 = 0
Х 1 =Х
Х=Х
Х =0

14. Логические функции

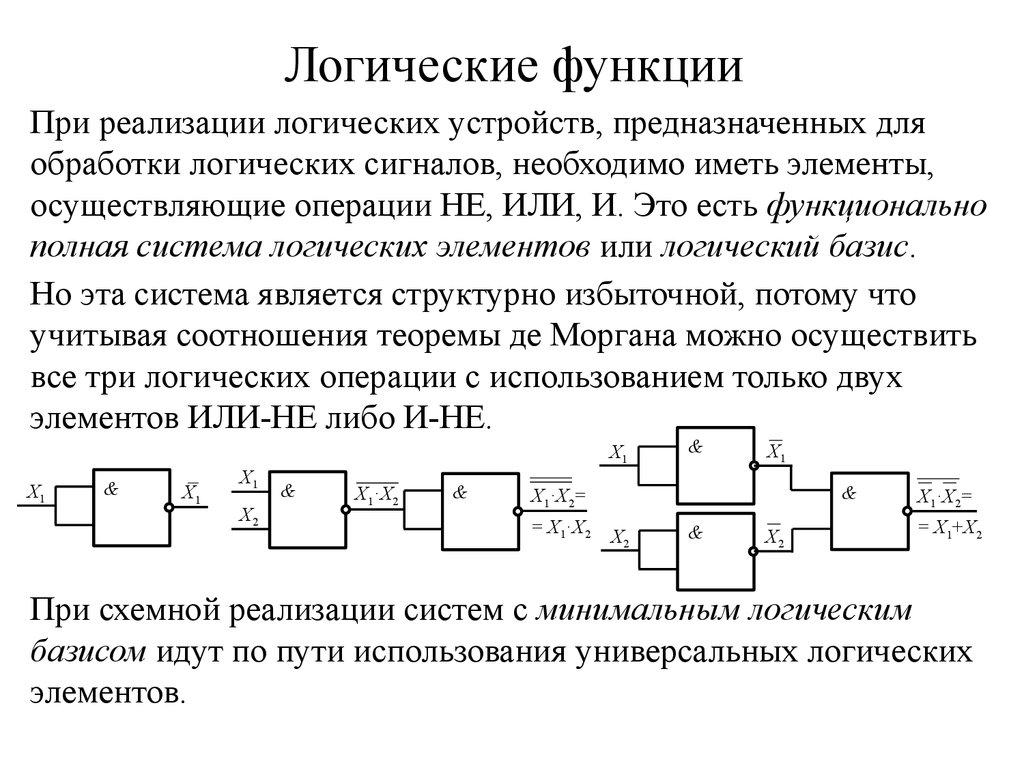
При реализации логических устройств, предназначенных для
обработки логических сигналов, необходимо иметь элементы,
осуществляющие операции НЕ, ИЛИ, И. Это есть функционально
полная система логических элементов или логический базис.
Но эта система является структурно избыточной, потому что
учитывая соотношения теоремы де Моргана можно осуществить
все три логических операции с использованием только двух
элементов ИЛИ-НЕ либо И-НЕ.
X1
&
–
X1
X1
X2
X1
&
X1·X2
&
&
X1
&
X1·X2=
= X1·X2
X2
&
X2
X1·X2=
= X1+X2
При схемной реализации систем с минимальным логическим
базисом идут по пути использования универсальных логических
элементов.

15. Логические функции

В общем случае логическая функция Y может зависеть от нескольких
переменных X1, X2, … , Xn. Наиболее часто связь между логической функцией
и логическими переменными задается в виде таблицы истинности или в
алгебраической форме. Определить структуру логического устройства
можно, исходя из алгебраической формы записи. Переход от таблицы
истинности к алгебраической форме записи осуществляется с
использованием совершенной конъюнктивной нормальной формы (СКНФ),
либо совершенной дизъюнктивной нормальной формы (СДНФ). Также
может использоваться метод карт Карно.
СДНФ – составляется сумма (дизъюнкция) произведений независимых
логических переменных, для которых функция принимает значение равное
единице. Если какая-либо переменная равна нулю, то берется ее инверсное
значение.
СКНФ – составляется произведение (конъюнкция) сумм логических
переменных, для которых логическая функция принимает значение равное
нулю. Если какая-либо переменная равна единице, то берется ее инверсное
значение.

16. Логические функции

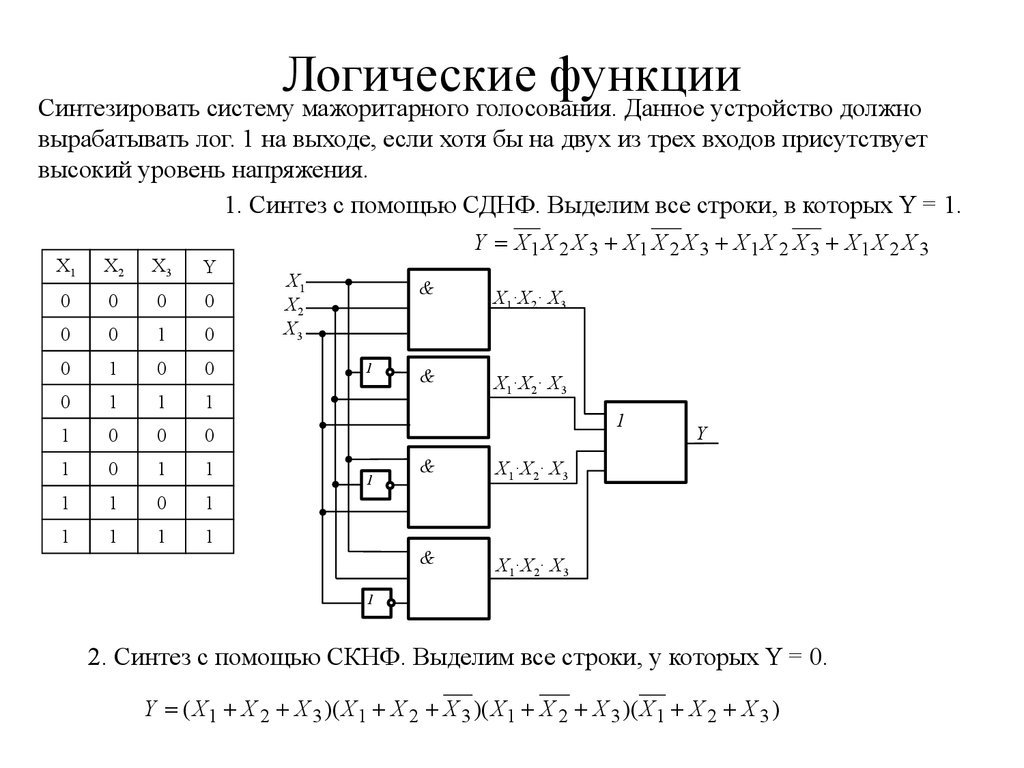
Синтезировать систему мажоритарного голосования. Данное устройство должно
вырабатывать лог. 1 на выходе, если хотя бы на двух из трех входов присутствует
высокий уровень напряжения.
1. Синтез с помощью СДНФ. Выделим все строки, в которых Y = 1.
X1
X2
X3
Y
0
0
0
0
0
0
1
0
0
1
0
0
0
1
1
1
1
0
0
0
1
0
1
1
1
1
0
1
1
1
1
1
Y X1 X 2 X 3 X1 X 2 X 3 X1 X 2 X 3 X1 X 2 X 3
Х1
Х2
Х3
1
&
Х1·Х2· Х3
&
Х1·Х2· Х3
1
1
&
Х1·Х2· Х3
&
Х1·Х2· Х3
Y
1
2. Синтез с помощью СКНФ. Выделим все строки, у которых Y = 0.
Y ( X 1 X 2 X 3 )( X 1 X 2 X 3 )( X 1 X 2 X 3 )( X 1 X 2 X 3 )

17. Минимизация логических функций

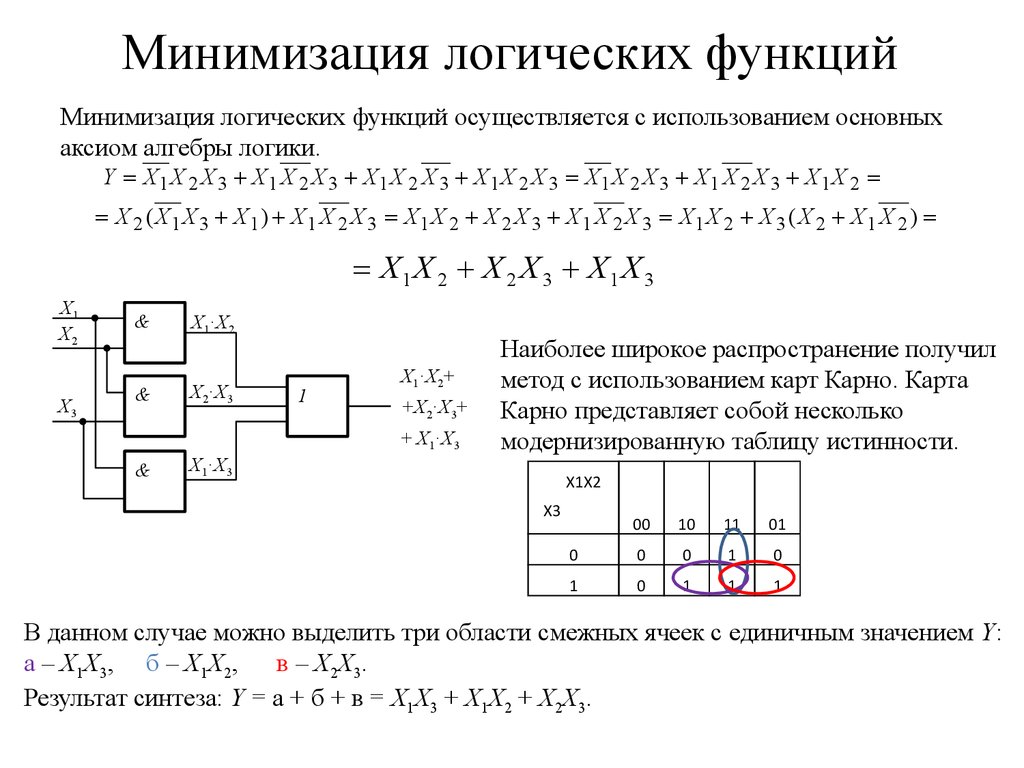
Минимизация логических функций осуществляется с использованием основных
аксиом алгебры логики.
Y X1 X 2 X 3 X1 X 2 X 3 X1 X 2 X 3 X1 X 2 X 3 X1 X 2 X 3 X1 X 2 X 3 X1 X 2
X 2 ( X1 X 3 X1 ) X1 X 2 X 3 X1 X 2 X 2 X 3 X1 X 2 X 3 X1 X 2 X 3 ( X 2 X1 X 2 )
X1 X 2 X 2 X 3 X1 X 3
Х1
Х2
Х3
&
&
Х1·Х2
Х2·Х3
1
Х1·Х2+
+Х2·Х3+
+ Х1·Х3
&
Х1·Х3
Наиболее широкое распространение получил
метод с использованием карт Карно. Карта
Карно представляет собой несколько
модернизированную таблицу истинности.
X1X2
X3
00
10
11
01
0
0
0
1
0
1
0
1
1
1
В данном случае можно выделить три области смежных ячеек с единичным значением Y:
а – X1X3, б – X1X2,
в – X2 X3 .
Результат синтеза: Y = а + б + в = X1X3 + X1X2 + X2X3.

18. Типы логических элементов

Существует несколько типов транзисторных логик, которые реализуют универсальные
логические элементы. Из основных можно выделить:
а) транзисторно-транзисторная логика (ТТЛ);
б) эмиттерно-связанная логика (ЭСЛ);
в)транзисторная логика на комплементарных ключах (КМДП (КМОП)).
Параметры логических элементов можно разделить:
а) статические (напряжение питания, уровни логических нуля и единицы, логический
перепад, токи);
б) динамические (быстродействие, определяемое скоростями перехода из одного
состояния в другое).

19. Триггеры

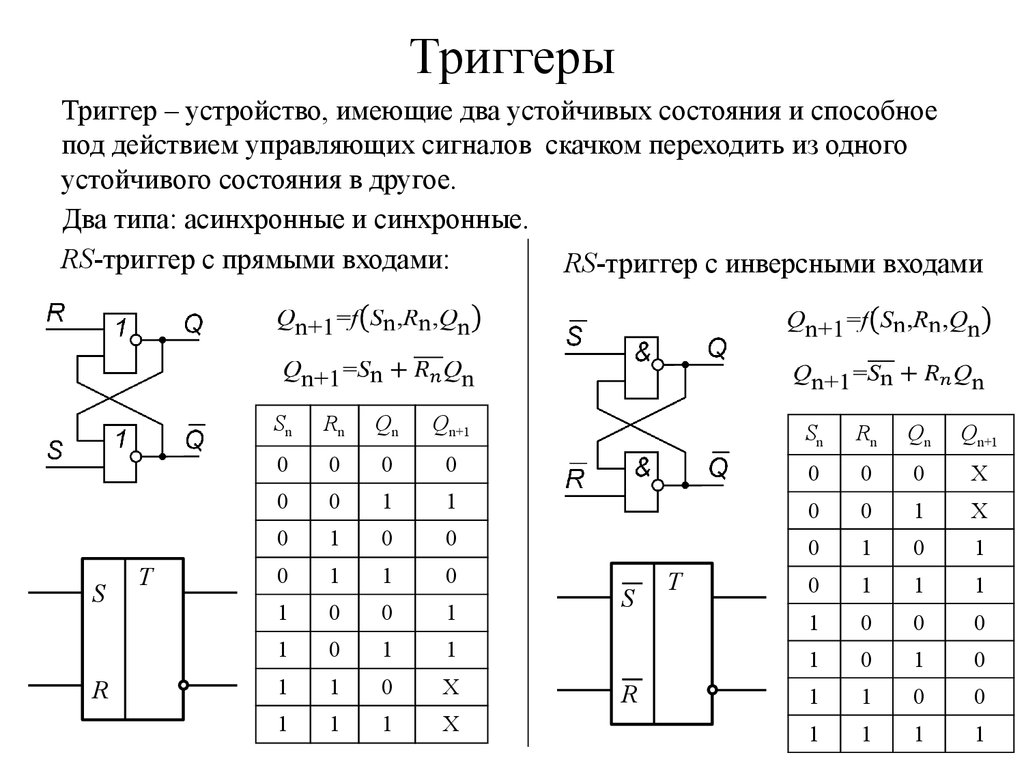
Триггер – устройство, имеющие два устойчивых состояния и способное
под действием управляющих сигналов скачком переходить из одного
устойчивого состояния в другое.
Два типа: асинхронные и синхронные.
RS-триггер с прямыми входами:
RS-триггер с инверсными входами
S
R
T
Sn
Rn
Qn
Qn+1
Sn
Rn
Qn
Qn+1
0
0
0
0
0
0
0
Х
0
0
1
1
0
0
1
Х
0
1
0
0
0
1
0
1
0
1
1
0
0
1
1
1
1
0
0
1
1
0
0
0
1
0
1
1
1
0
1
0
1
1
0
X
1
1
0
0
1
1
1
X
1
1
1
1
S
R
T

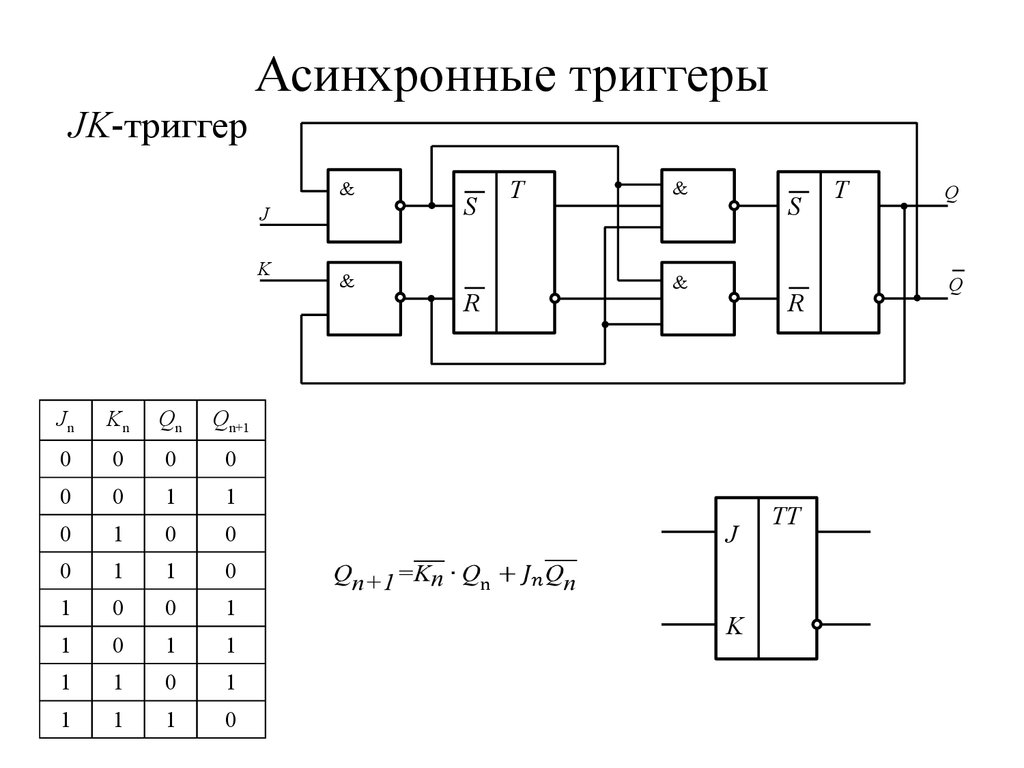
20. Асинхронные триггеры

JK-триггер
&
J
K
Jn
Kn
Qn
Qn+1
0
0
0
0
0
0
1
1
0
1
0
0
0
1
1
0
1
0
0
1
1
0
1
1
1
1
0
1
1
1
1
0
&
S
R
T
&
S
&
R
J
K
TT
T
Q
Q

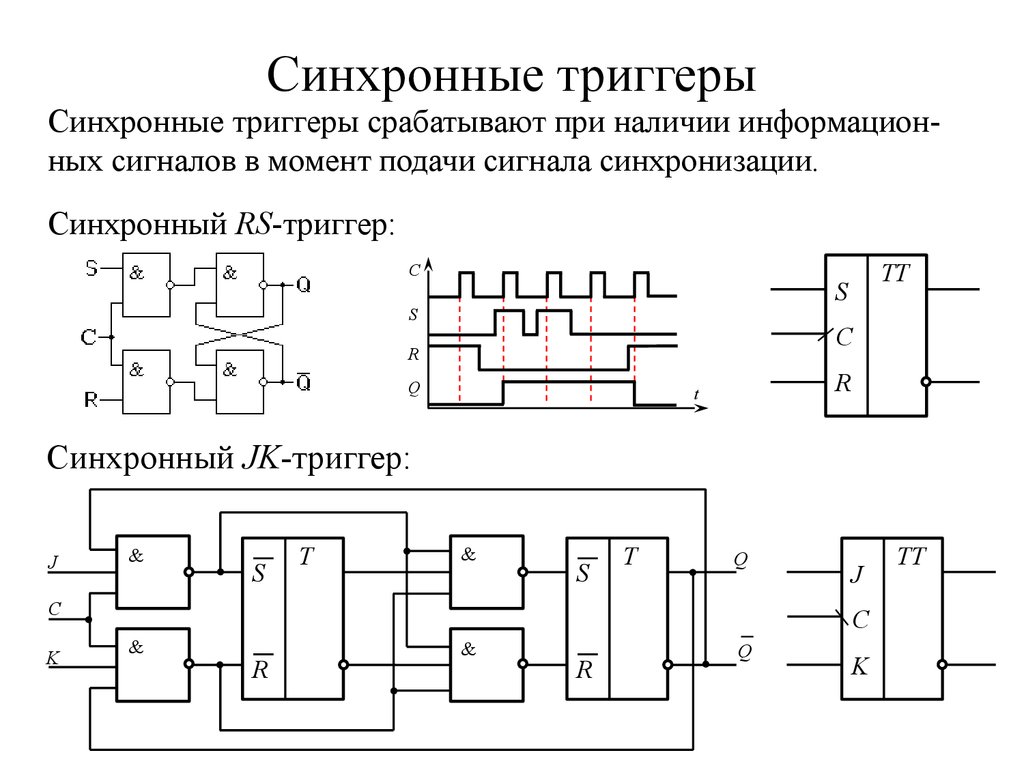
21. Синхронные триггеры

Синхронные триггеры срабатывают при наличии информационных сигналов в момент подачи сигнала синхронизации.
Синхронный RS-триггер:
C
TT
S
S
C
R
Q
R
t
Синхронный JK-триггер:
J
&
S
T
&
S
T
Q
C
K
J
C
&
R
&
R
Q
K
TT

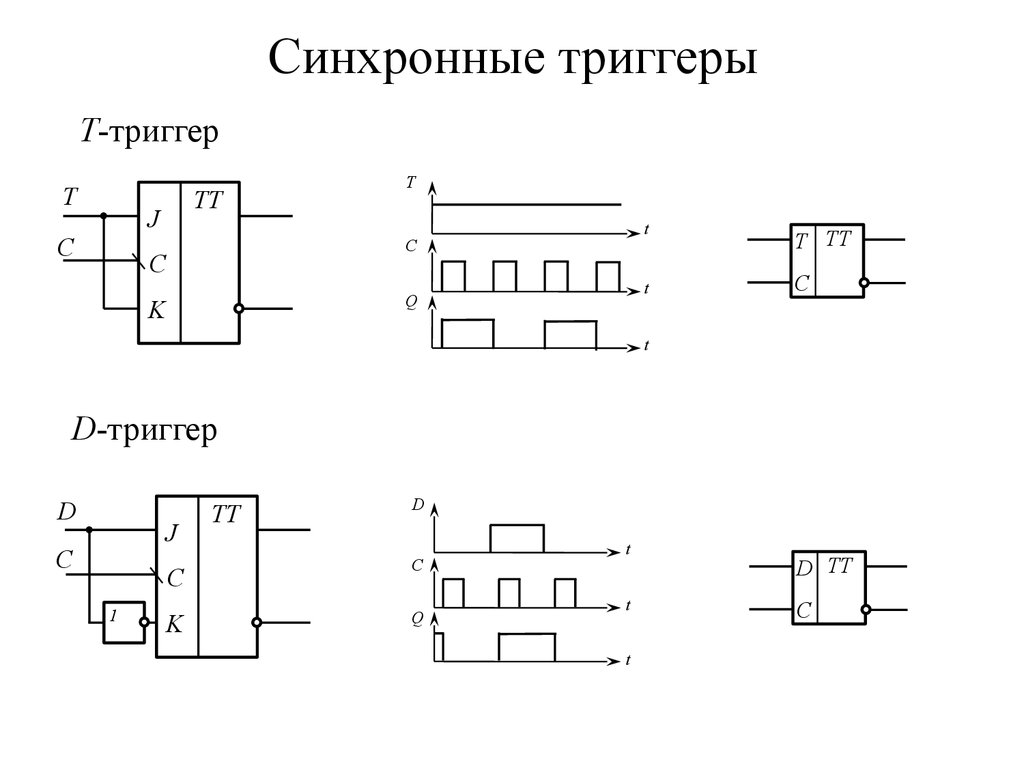
22. Синхронные триггеры

Т-триггер
T
TT
J
C
T
C
C
Q
K
t
T TT
t
C
t
D-триггер
D
J
C
1
TT
D
C
C
K
Q
t
t
t
D TT
C

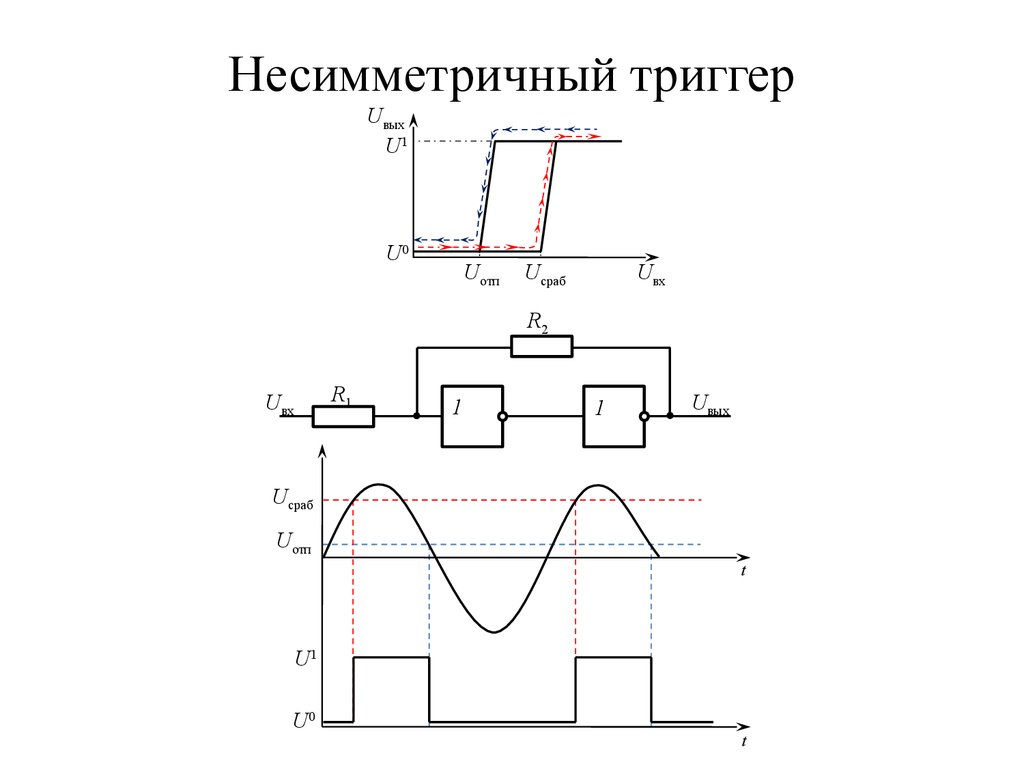
23. Несимметричный триггер

Uвых
U1
U0
Uотп
Uсраб
Uвх
R2
R1
Uвх
1
1
Uвых
Uсраб
Uотп
t
U1
U0
t

24. Цифровые функциональные узлы

Это устройство, предназначенное для выполнения определенных
действий с двоичными переменными: сложение, преобразование,
счет, прием, передачу и хранение цифровой информации.
Два класса функциональных узлов:
– комбинационный тип;
– последовательностный тип.
Комбинационными называются функциональные узлы, выходной
сигнал которых определяется комбинацией логических сигналов
на входах, действующих в данный момент времени.
Последовательностными называются функциональные узлы,
выходной сигнал которых зависит не только от значений входных
сигналов, действующих в данный момент времени, но и от
предыдущих значений.

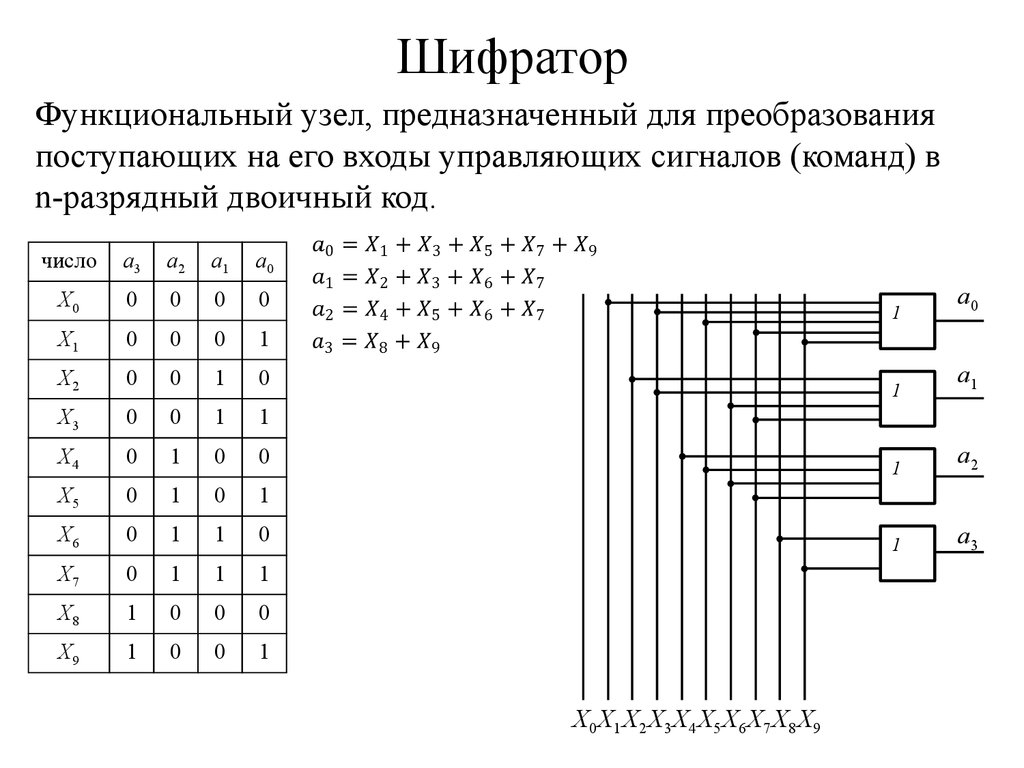
25. Шифратор

Функциональный узел, предназначенный для преобразования
поступающих на его входы управляющих сигналов (команд) в
n-разрядный двоичный код.
число
a3
a2
a1
a0
X0
0
0
0
0
X1
0
0
0
1
X2
0
0
1
0
X3
0
0
1
1
X4
0
1
0
0
X5
0
1
0
1
X6
0
1
1
0
X7
0
1
1
1
X8
1
0
0
0
X9
1
0
0
1
X0 X1 X2 X3 X4 X5 X6 X7 X8 X9
1
a0
1
a1
1
a2
1
a3

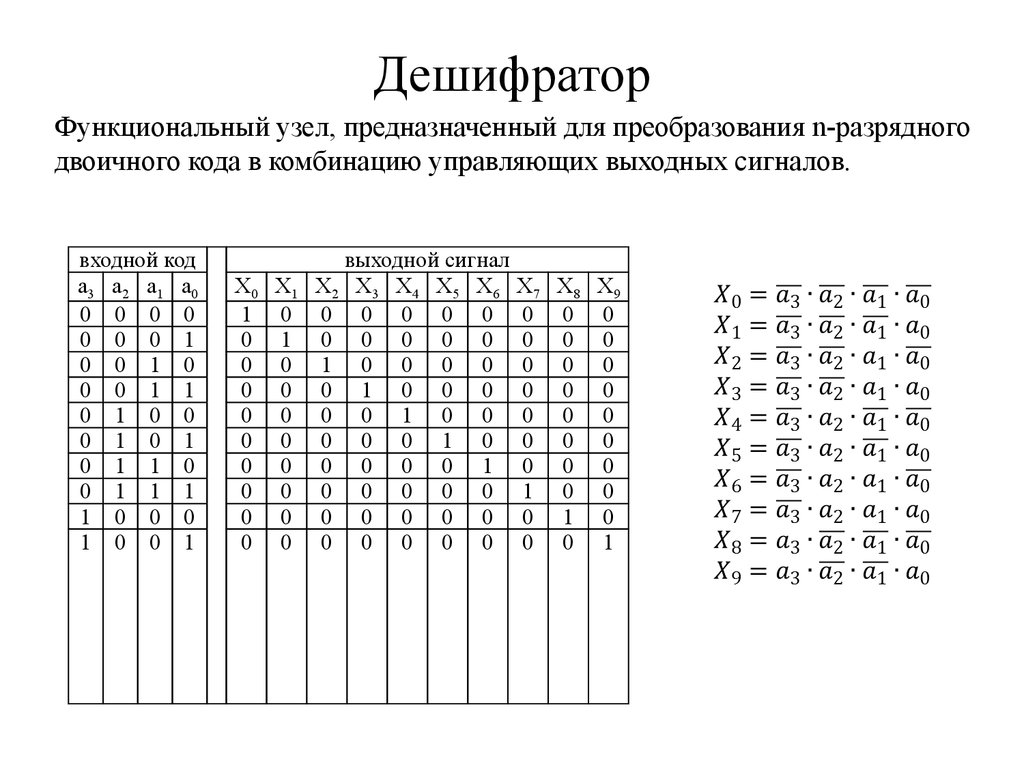
26. Дешифратор

Функциональный узел, предназначенный для преобразования n-разрядного
двоичного кода в комбинацию управляющих выходных сигналов.
входной код
a3 a2 a1 a0
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
X0 X1
1 0
0 1
0 0
0 0
0 0
0 0
0 0
0 0
0 0
0 0
выходной сигнал
X2 X3 X4 X5 X6 X7 X8 X9
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0
0 1 0 0 0 0 0 0
0 0 1 0 0 0 0 0
0 0 0 1 0 0 0 0
0 0 0 0 1 0 0 0
0 0 0 0 0 1 0 0
0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 1

27. Дешифратор

a0 a1
a2 a3
00
10
11
01
00
10
11
01
X0
X4
X1
X5
X3
X7
X2
X6
1
X8
1
X9
1
1
1
1
&
X0
&
X1
&
&
&
&
1
a3
1
a2
1
a1
1
a0
.
.
.
.
.
.
X4
X5
X8
X9

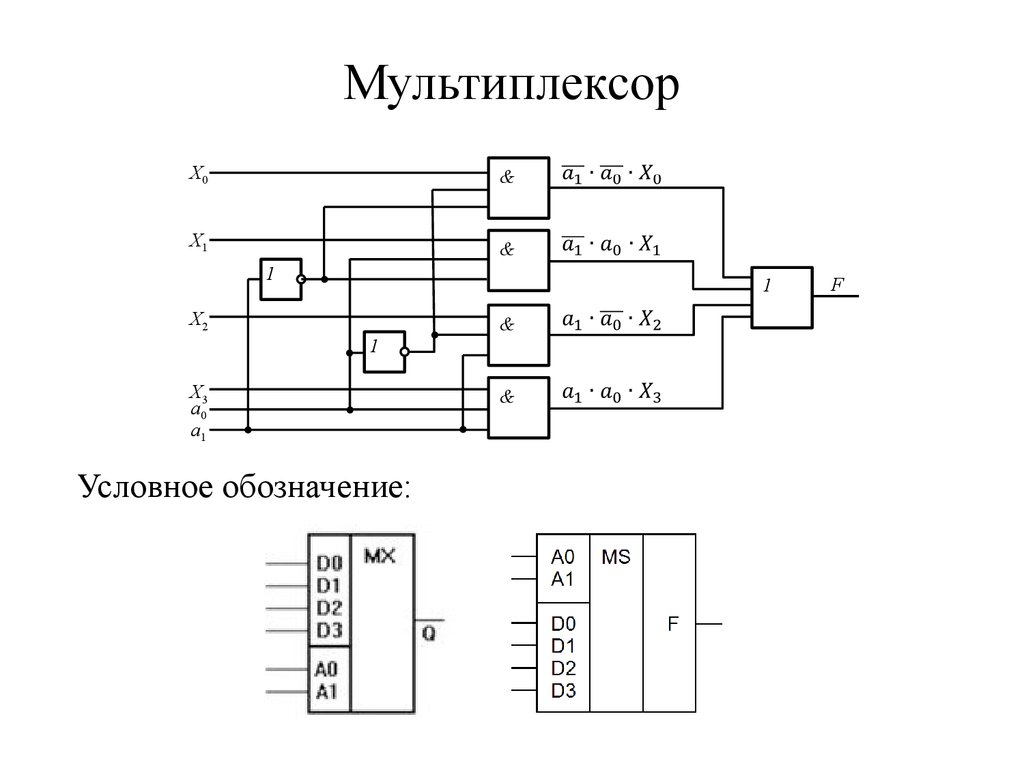
28. Мультиплексор

Функциональный узел, который осуществляет управляемую
коммутацию информации, поступающей по N входным линиям,
на одну выходную линию. Коммутация определенной входной
линии происходит в соответствии с двоичным адресным кодом.
Если адресный код имеет n разрядов, то можно осуществить
N = 2n комбинаций адресных сигналов.
Рассмотрим n = 2, N = 4. F – значение информации.
Таблица функционирования будет следующей:
a1
a0
F
0
0
X0
0
1
X1
1
0
X2
1
1
X3

29. Мультиплексор

X0
&
X1
&
1
1
X2
&
1
X3
a0
a1
Условное обозначение:
&
F

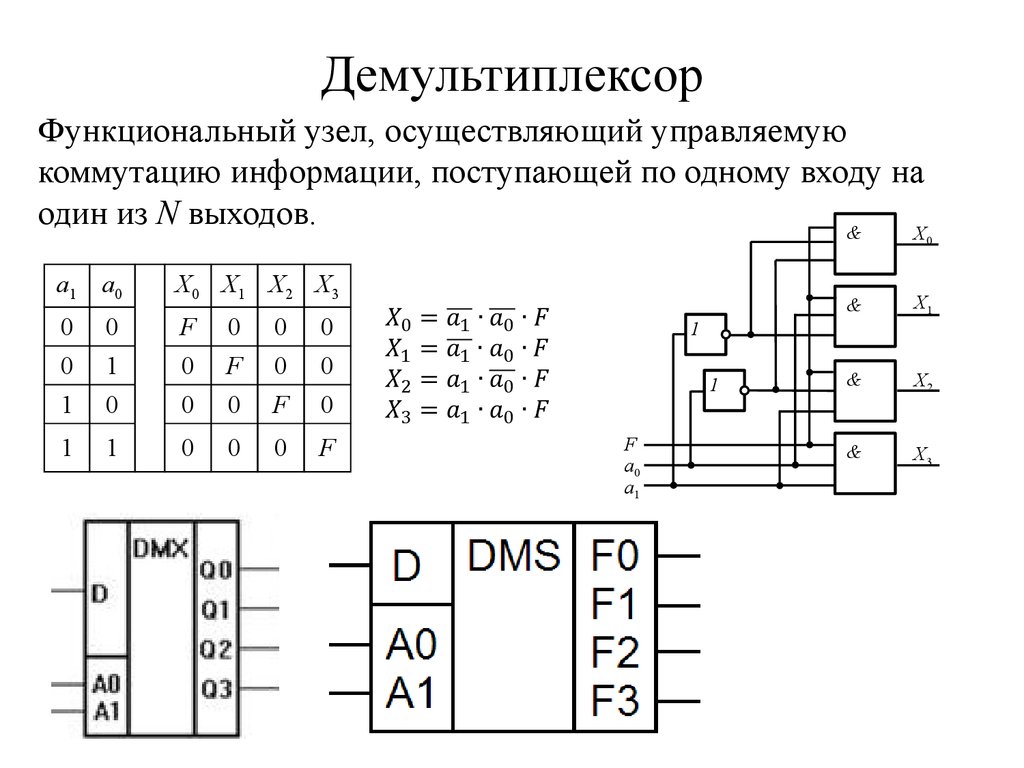
30. Демультиплексор

Функциональный узел, осуществляющий управляемую
коммутацию информации, поступающей по одному входу на
один из N выходов.
&
X
a1 a0
X0 X1 X2 X3
0
0
F
0
0
0
0
1
0
F
0
0
1
0
0
0
F
0
1
1
0
0
0
F
0
&
X1
&
X2
&
X3
1
1
F
a0
a1

31. Сумматор

Функциональный узел, выполняющий арифметическое сложение кодов двух
чисел.
По количеству одновременно обрабатываемых разрядов складываемых
чисел:
– одноразрядные,
– многоразрядные.
По числу входов и выходов одноразрядных двоичных сумматоров:
– четвертьсумматоры;
– полусумматоры;
– полные одноразрядные двоичные сумматоры.
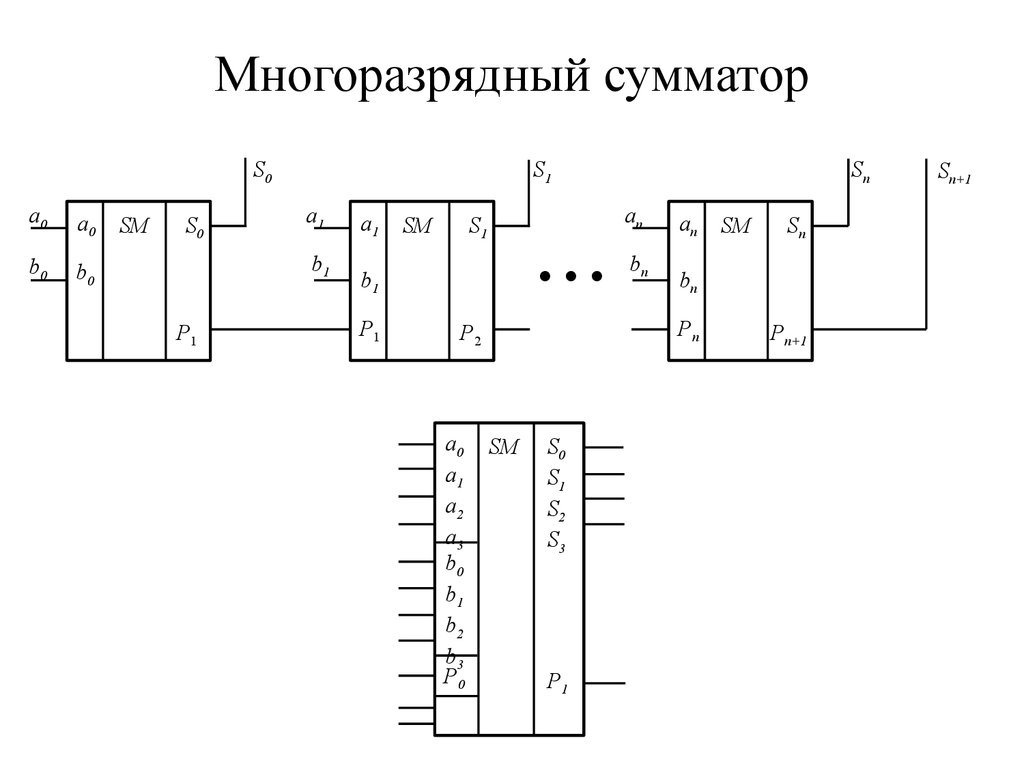
По способу представления и обработки складываемых чисел многоразрядные сумматоры подразделяются на:
– последовательные, в которых обработка чисел ведется поочередно, разряд за
разрядом на одном и том же оборудовании;
– параллельные, в которых слагаемые складываются одновременно по всем
разрядам, и для каждого разряда имеется свое оборудование.

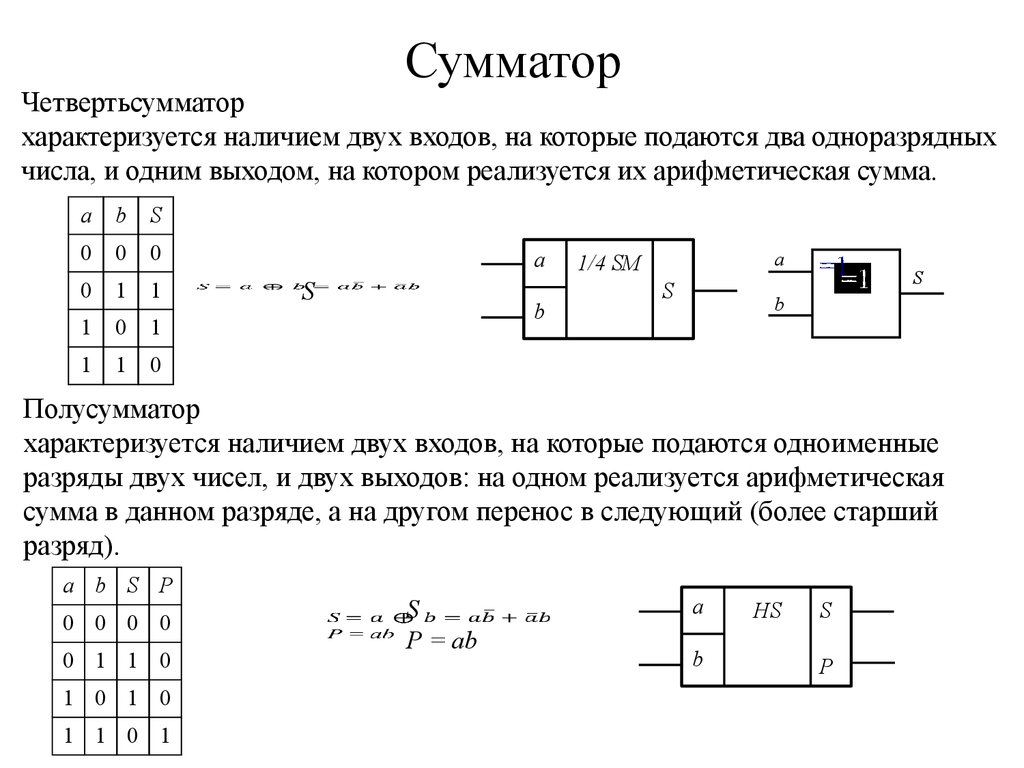
32. Сумматор

Четвертьсумматор
характеризуется наличием двух входов, на которые подаются два одноразрядных
числа, и одним выходом, на котором реализуется их арифметическая сумма.
a
b
S
0
0
0
0
1
1
1
0
1
1
1
0
a
S
b
a
1/4 SM
S
S
b
Полусумматор
характеризуется наличием двух входов, на которые подаются одноименные
разряды двух чисел, и двух выходов: на одном реализуется арифметическая
сумма в данном разряде, а на другом перенос в следующий (более старший
разряд).
a b S P
0 0 0 0
0 1 1 0
1 0 1 0
1 1 0 1
S
P = ab
a
b
HS
S
P

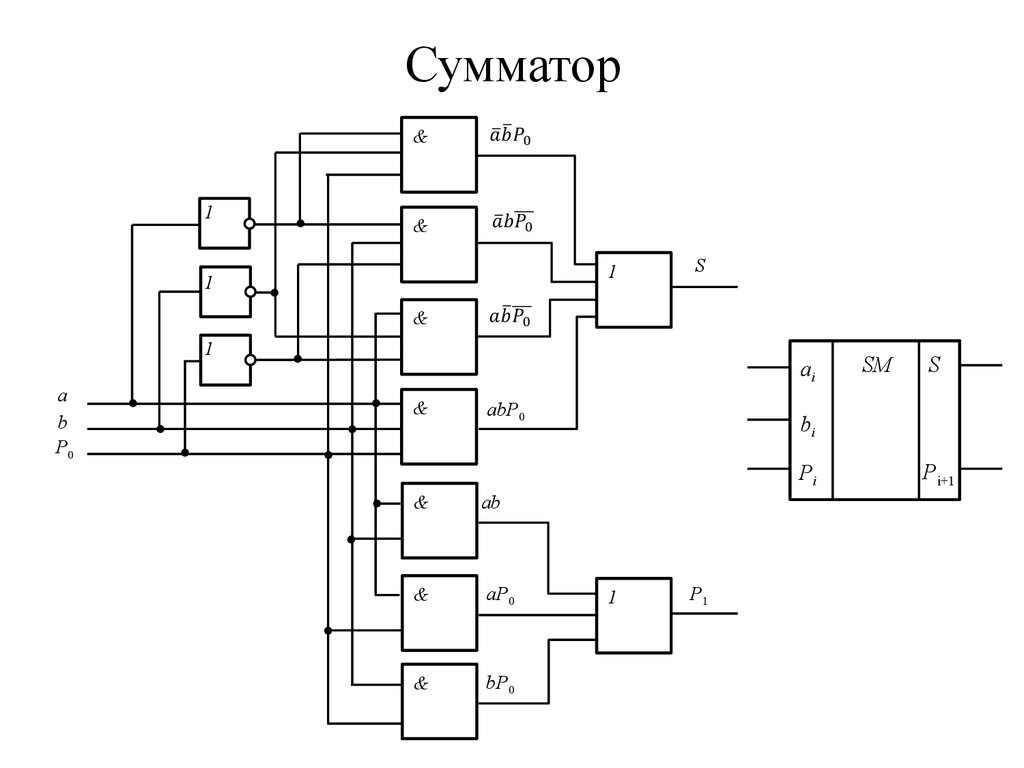
33. Сумматор

Полный одноразрядный двоичный сумматор
характеризуется наличием трех входов, на которые подаются одноименные
разряды двух складываемых чисел и перенос из предыдущего (более младшего)
разряда, и двумя выходами: на одном реализуется арифметическая сумма в
данном разряде, а на другом перенос в следующий (более старший разряд).
Для S:
ab
00 10 11 01
P0
a
b
P0
S
P1
0
0
0
0
0
0
0
1
1
0
0
0
1
0
1
0
1
0
1
0
1
1
0
1
0
0
1
1
0
1
1
0
0
1
0
1
0
1
0
1
1
1
0
0
1
1
1
1
1
1
Для P1:
ab
00 10 11 01
P0
0
0
0
1
0
1
0
1
1
1
S

34. Сумматор

&
1
&
1
1
S
&
1
a
b
P0
ai
&
abP0
ab
&
aP0
&
bP0
S
bi
Pi
&
SM
1
P1
Pi+1

35. Многоразрядный сумматор

S0
a0
a0
b0
b0
SM
S0
S1
a1
b1
P1
a1
SM
…
S1
b1
P1
an
bn
an
SM
S0
S1
S2
S3
P1
SM
Sn
bn
Pn
P2
a0
a1
a2
a3
b0
b1
b2
b3
P0
Sn
Pn+1
Sn+1

36. Функциональные узлы последовательностного типа

Регистры
Функциональный узел, осуществляющий прием, хранение и
передачу информации.
2 типа регистров:
– регистры с последовательным приемом и выдачей
информации (сдвиговые регистры);
– регистры с параллельным приемом и выдачей информации
(регистры памяти).

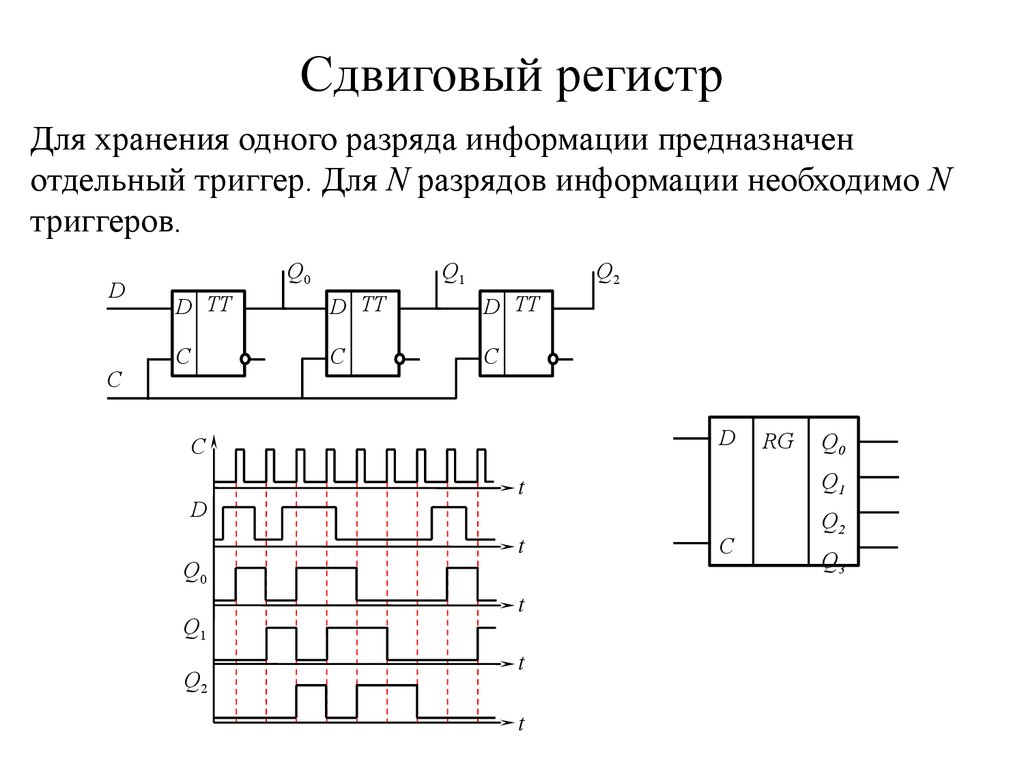
37. Сдвиговый регистр

Для хранения одного разряда информации предназначен
отдельный триггер. Для N разрядов информации необходимо N
триггеров.
D
С
Q0
Q1
Q2
D TT
D TT
D TT
C
C
C
D
С
D
Q0
Q1
Q2
t
t
t
Q0
Q1
t
t
RG
C
Q2
Q3

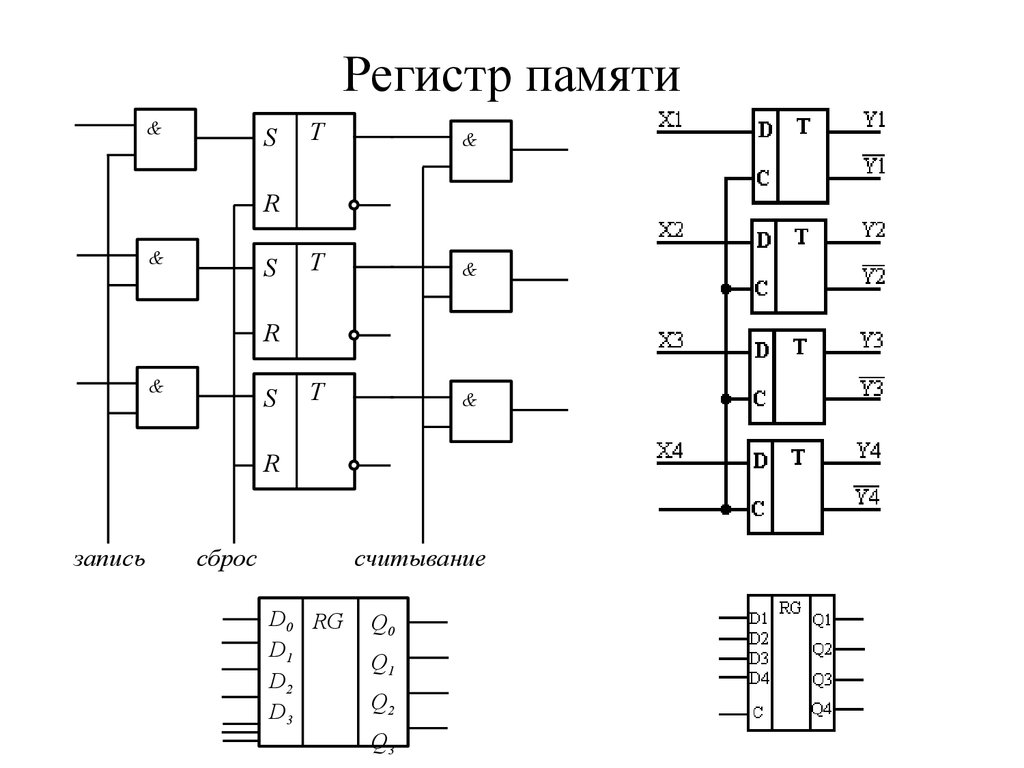
38. Регистр памяти

&
S
T
&
T
&
T
&
R
&
S
R
&
S
R
запись
сброс
считывание
D0 RG
D1
D2
D3
Q0
Q1
Q2
Q3

39. Счетчики

Функциональный узел, предназначенный для подсчета количества
импульсов.
2 класса счетчиков: двоичные и недвоичные.
Основные параметры: коэффициент пересчета и быстродействие.
Коэффициент пересчета Ксч – максимальное число импульсов,
которое может быть подсчитано данным счетчиком, и зависит от
количества разрядов n (Ксч = 2n).
Быстродействие счетчика определяется двумя величинами: разрешающей способностью и временем установки очередного
состояния. Разрешающая способность tp = 1/fсч (fсч – частота
следования входных импульсов) определяется минимально
допустимым временным интервалом между двумя выходными
импульсами, при котором не происходит потери счета (сбоя). Время
установки представляет собой интервал времени между поступлением
импульса на вход счетчика и переходом его в новое состояние.

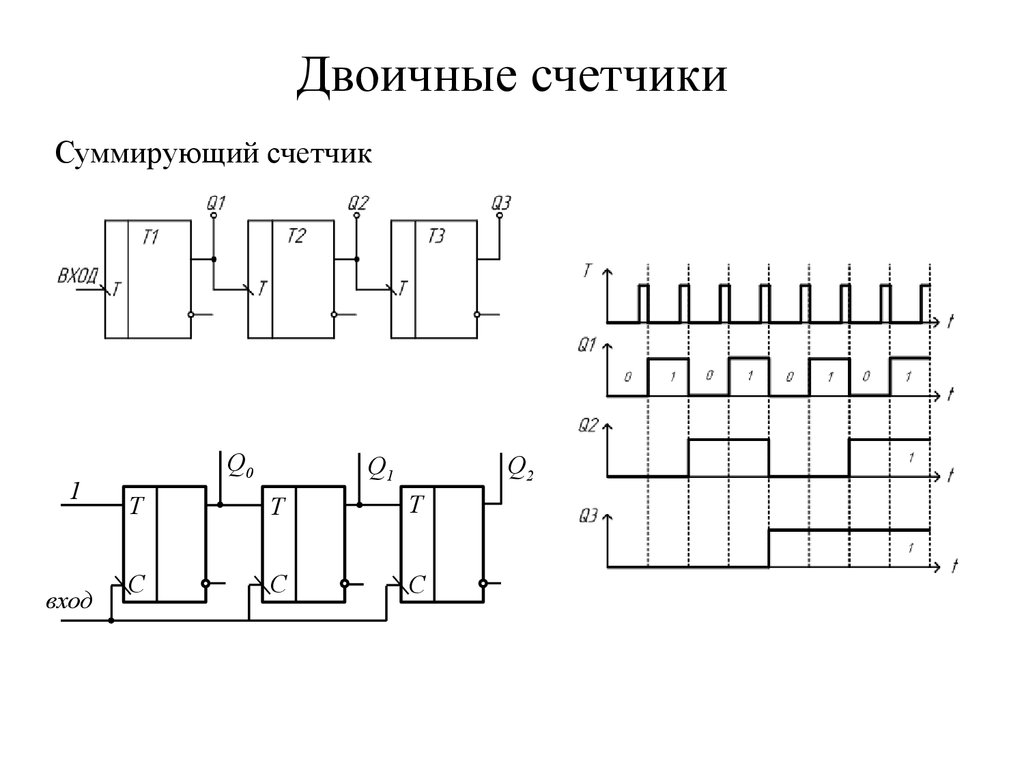
40. Двоичные счетчики

Суммирующий счетчик
1
вход
Q0
Q2
Q1
T
T
T
C
C
C

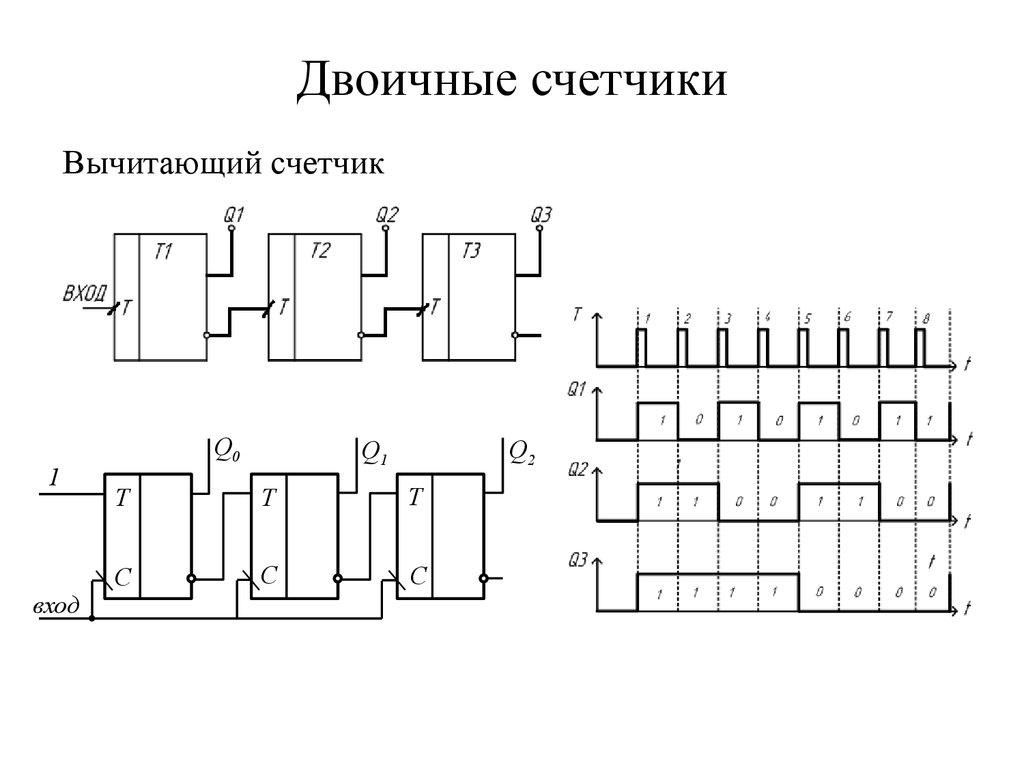
41. Двоичные счетчики

Вычитающий счетчик
1
вход
Q0
Q2
Q1
T
T
T
C
C
C

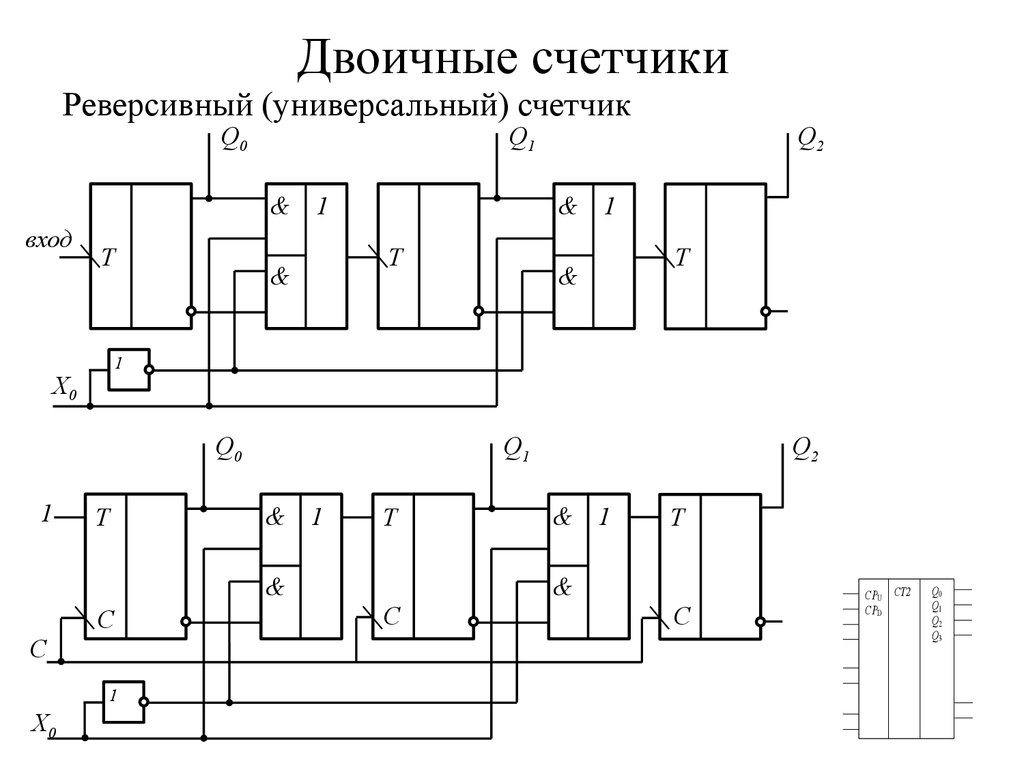
42. Двоичные счетчики

Реверсивный (универсальный) счетчик
Q0
Q1
& 1
вход
T
&
& 1
T
Q0
T
Q1
& 1
T
&
C
C
1
X0
&
T
1
X0
1
Q2
Q2
& 1
T
&
C
C
CPU CT2
CPD
Q0
Q1
Q2
Q3

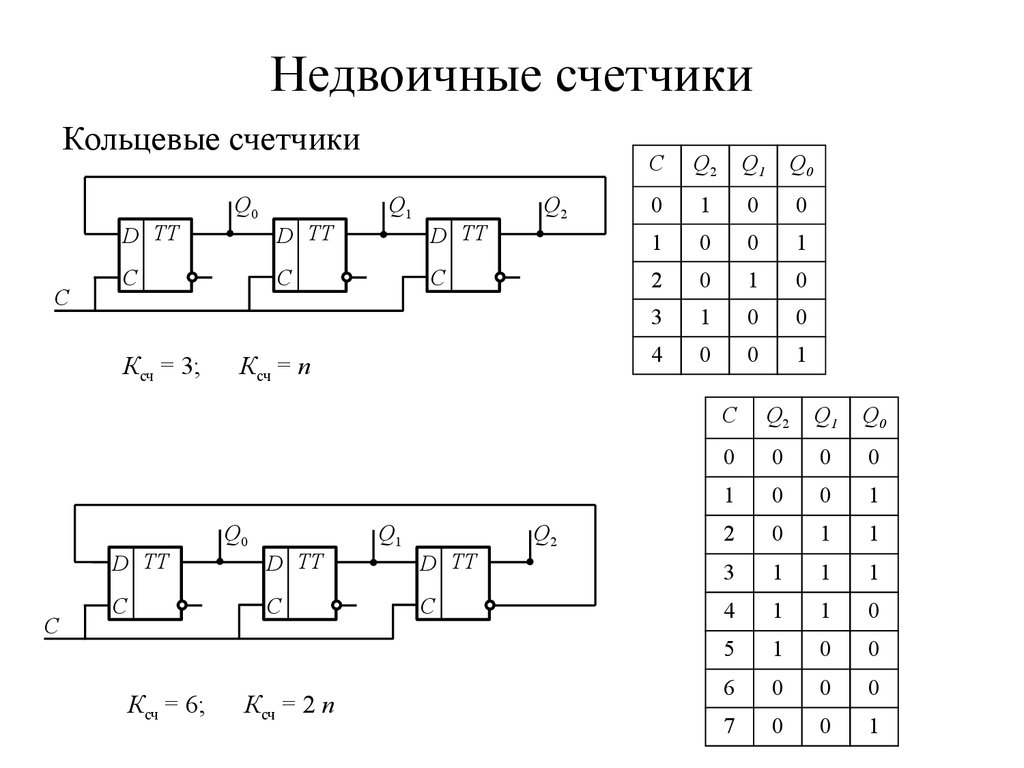
43. Недвоичные счетчики

Кольцевые счетчики
D TT
С
C
Ксч = 3;
D TT
С
Q0
C
Ксч = 6;
D TT
Q1
C
D TT
Q2
C
Ксч = n
Q0
D TT
C
Ксч = 2 n
Q1
D TT
C
Q2
С
Q2
Q1
Q0
0
1
0
0
1
0
0
1
2
0
1
0
3
1
0
0
4
0
0
1
С
Q2
Q1
Q0
0
0
0
0
1
0
0
1
2
0
1
1
3
1
1
1
4
1
1
0
5
1
0
0
6
0
0
0
7
0
0
1

44. Недвоичные счетчики

Счетчики с обратными связями
На примере Ксч = 5.
Имп. Q2n Q1n Q0n Q2n+1 Q1n+1 Q0n+1
1
2
3
4
5
0
0
0
0
1
0
0
1
1
0
Для FQ0:
0
1
0
1
0
0
0
0
1
0
0
1
1
0
0
FQ2 FQ1 FQ0
0
0
0
1
0
1
0
0
FQ1 :
0
0
1
0
FQ2:
Q0 Q1
Q0 Q1
Q2 00 10 11 01
Q0 Q1
Q2 00 10 11 01
Q2 00 10 11 01
0
0
0
1
0
0
0
0
1
0
Х
Х
Х
1
0
X
X
X
1
X
X
X

45. Недвоичные счетчики

Для J0:
J 1:
J2:
Q0 Q1
Q0 Q1
Q0 Q1
Q2 00 10 11 01
Q2 00 10 11 01
Q2 00 10 11 01
0
X
X
X
1
0
0
1
X
X
0
0
0
1
0
1
0
Х
Х
Х
K1 :
1
0
X
X
X
K2:
1
X
X
X
X
Для K0:
Q0 Q1
Q0 Q1
Q0 Q1
Q2 00 10 11 01
Q2 00 10 11 01
Q2 00 10 11 01
0
X
1
1
X
0
X
X
1
0
0
X
X
X
X
1
X
Х
Х
Х
1
X
X
X
X
1
1
X
X
X
J 0 Q2;
K 0 1;
J1 K1 Q0;
J 2 Q0Q1;
K 2 1.

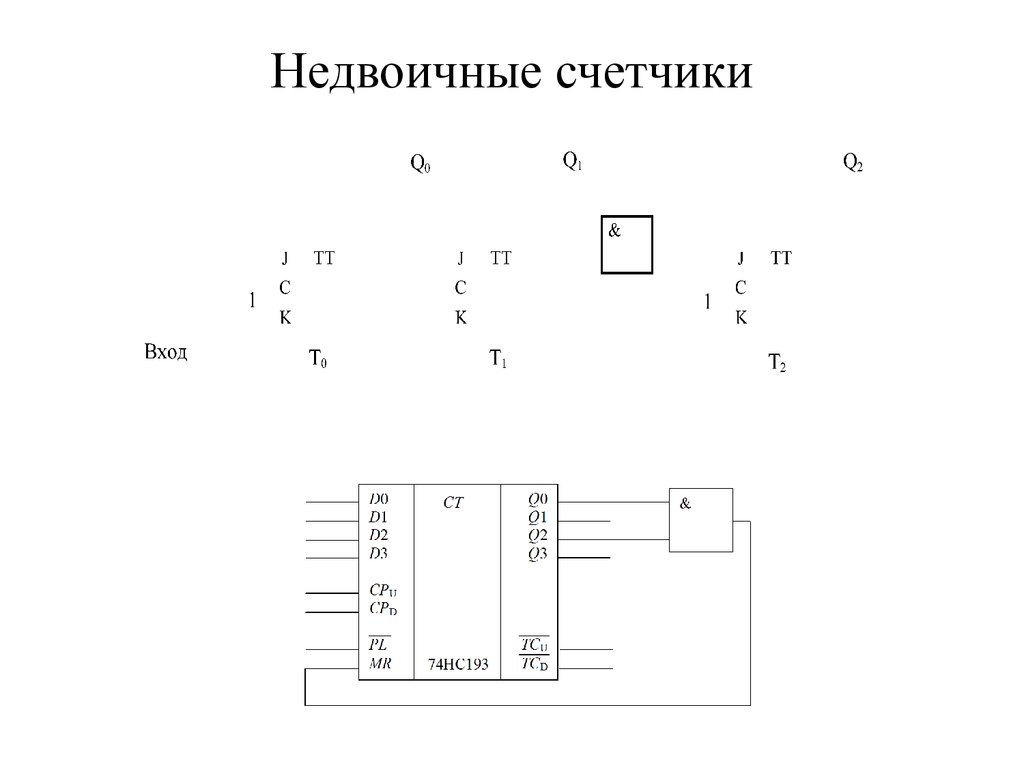
46. Недвоичные счетчики

47. Цифро-аналоговый преобразователь (ЦАП)

Идея заключается в получении мгновенного значения аналогового сигнала,
соответствующего входному цифровому коду, путем суммирования эталонных токов с
последующим преобразованием их в напряжение. Управление эталонными токами
или эталонными напряжениями осуществляется с помощью двоичного кода.
Величины эталонных напряжений нормируются.
Старшему разряду СР соответствует
максимальное значение эталонного
напряжения:
1
U1 U ср U п ш .
2
U 2 U пш / 4
U n U пш / 2 n
1
1 1
U вых ... n U пш 1 2 n U пш
2
2 4
7
1 1 1
Если три разряда, то U вых U пш U пш
8
2 4 8

48. ЦАП с резисторами веса

i0 i1 i2 ... ii ... in .
U вых U оп U оп
U
U
... оп ... оп .
R0
R1
R2
Ri
Rn
R
ΔU вых 0 U оп
Ri
R R
R
R
U вых U оп 0 0 ... 0 ... 0
Ri
Rn
R1 R2
i0
R0 1
R1 2
R1 2 R0 , R2 4 R0 Rn 2n
1
1 1
U вых U оп ... n U оп 1 - 2- n
2
2 4
Погрешность воспроизведения определяется весом младшего разряда.
Для практической реализации схемы ЦАП с резисторами веса требуется большое
количество резисторов с разными значениями сопротивлений.

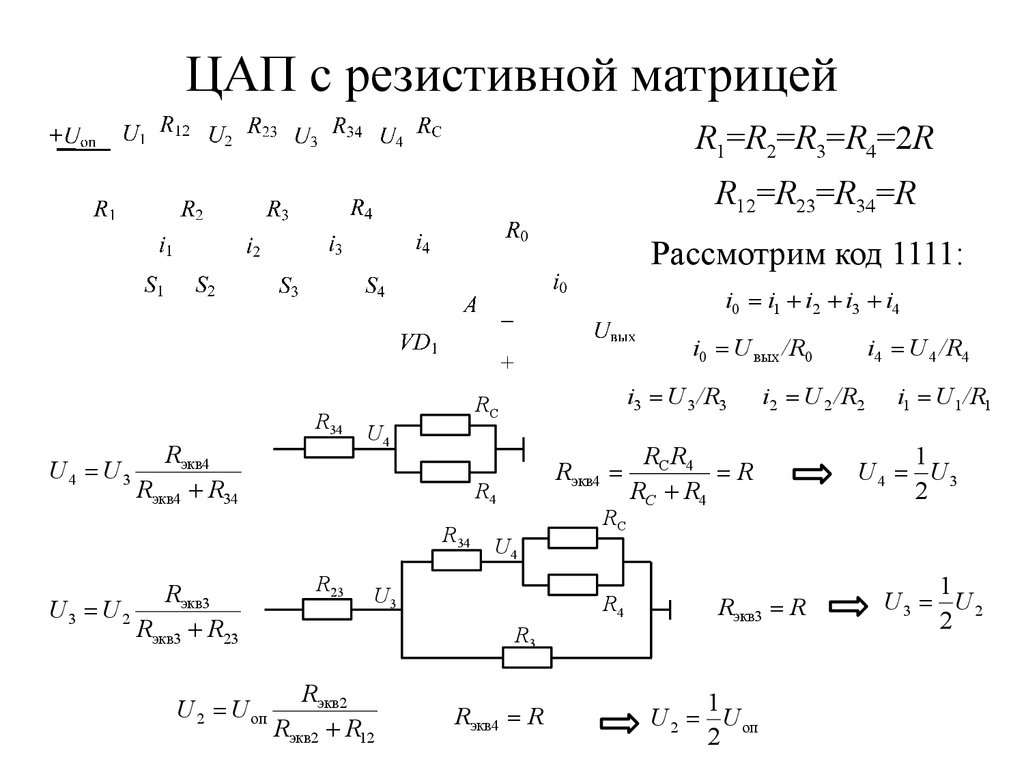
49. ЦАП с резистивной матрицей

R1=R2=R3=R4=2R
R12=R23=R34=R
Рассмотрим код 1111:
i0 i1 i2 i3 i4
i0 U вых /R0
R34
U 4 U3
Rэкв4
Rэкв4 R34
U4
U 2 U оп
Rэкв4
R4
R34
Rэкв3
U3 U2
Rэкв3 R23
i3 U 3 /R3
RC
R23
U4
U3
R4
R3
Rэкв2
Rэкв2 R12
RC
Rэкв4 R
i2 U 2 /R2
RC R4
R
RC R4
Rэкв3 R
1
U 2 U оп
2
i4 U 4 /R4
i1 U1 /R1
1
U4 U3
2
1
U3 U2
2

50. ЦАП с резистивной матрицей

Следовательно: U2=2U3=4U4
и, соответственно
i2 2i3 4i4.
Uоп= U1=2U2=4U3=8U4
i1
U1 U оп
U
U
U U
U
U
; i2 2 оп ; i3 3 оп ; i4 4 оп .
R1 2 R
R2 4 R
R3 8 R
R4 16 R
1 1 1 1
U вых R0 in U оп .
n 1
2 4 8 16
4
Преимущество: нет бросков токов.
Недостаток: постоянно протекает ток, что ведет к большим
затратам энергии.

51. Параметры ЦАП

Разрешение – количество разрядов входного двоичного кода.
Шагом квантования – расчетное приращение выходного напряжения ЦАП при
изменении входного кода на единицу младшего разряда (1 МР). Из формулы (11.1) для
двух кодов, отличающихся на единицу младшего разряда, получим: h = Uоп Rо.с /R(2b – 1).
Погрешность смещения нуля (δOFF) – смещение выходного напряжения ЦАП
относительно нуля в начальной точке преобразования.
Погрешность коэффициента передачи, или погрешность наклона (δG) – смещение
выходного напряжения ЦАП относительно значения Uоп в конечной точке
преобразования.
Нелинейностью (интегральная нелинейность) (δL) называется максимальное отклонение
реальной характеристики ЦАП от теоретической прямой, соединяющей нулевое и
максимальное значения выходного сигнала.
Дифференциальной нелинейностью преобразования (δLD) называется отклонение шага
преобразования ЦАП от идеального, который должен точно соответствовать 1 МР.
Динамические параметры:
время установления выходного сигнала tc – интервал времени от момента подачи
цифрового кода на вход ЦАП до момента появления выходного аналогового сигнала,
отличающегося от окончательного на некоторую величину (обычно 1 МР);
максимальная частота преобразования – наибольшая частота дискретизации, при
котором параметры ЦАП соответствуют заданным значениям.

52. Аналого-цифровой преобразователь (АЦП)

Существуют три основных типа аналого-цифровых преобразователей:
– АЦП последовательных приближений обладают сравнительно высоким
быстродействием и точностью, преобразуемый аналоговый сигнал последовательно
сравнивается с весовыми значениями напряжений, которые соответствуют весовым
коэффициентам разрядов.
– АЦП параллельного преобразования, входной аналоговый сигнал одновременно
(параллельно) сравнивается с 2n-1 градациями опорного напряжения, образуемыми
резистивным делителем. Получаемый результат сравнения преобразуется в
параллельный n–разрядный двоичный код. Такие АЦП обладают максимальным
быстродействием.
– АЦП с двойным интегрированием: на первом этапе происходит интегрирование
входного аналогового сигнала за определенный промежуток времени. Затем
осуществляется интегрирование противоположного по знаку известного
постоянного напряжения и фиксируется интервал времени, за который выходное
напряжение станет равным нулю, путем подсчета импульсов, следующих с
известной частотой. Зафиксированное счетчиком число импульсов представляется в
виде кода.

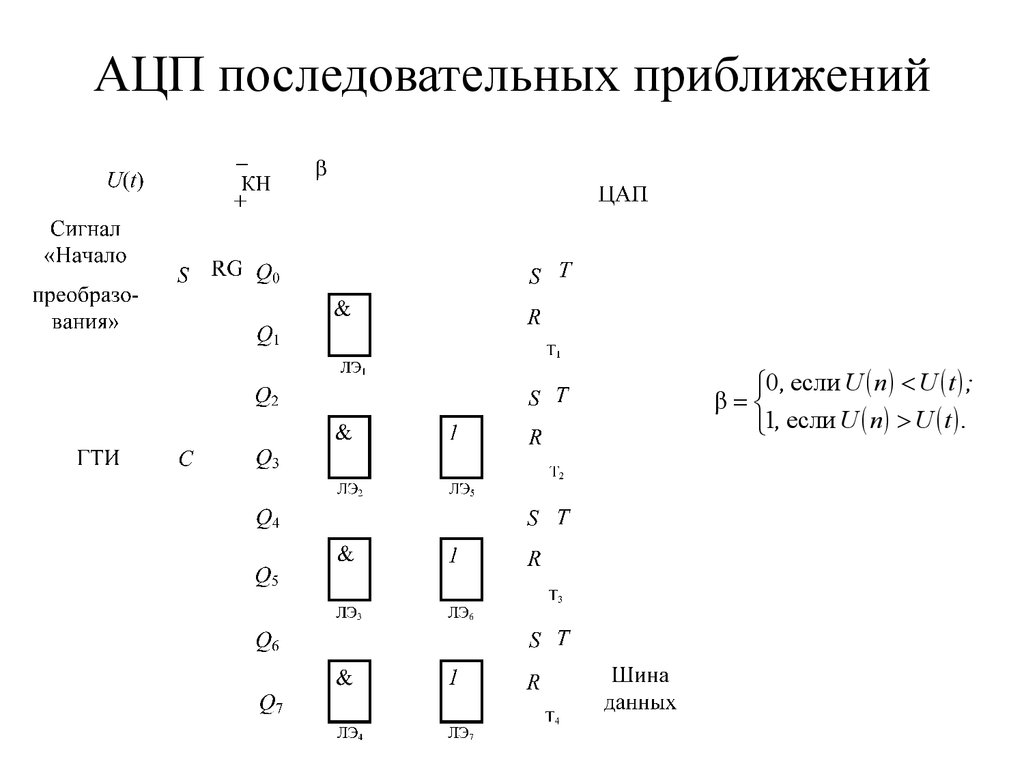
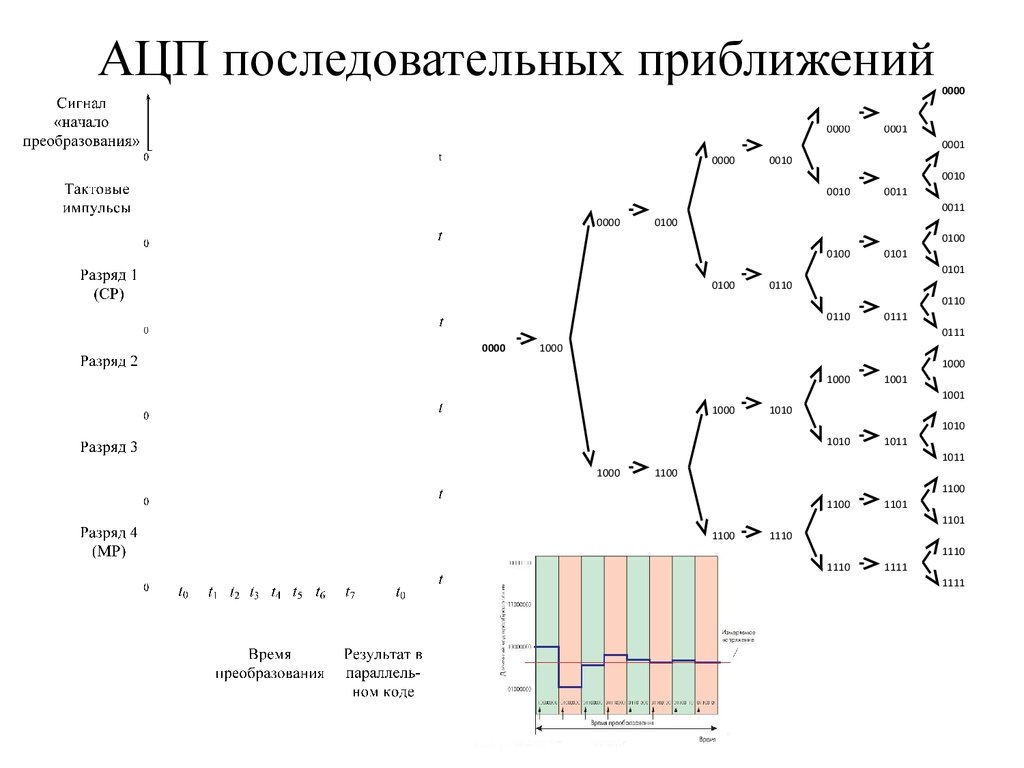
53. АЦП последовательных приближений

0 , если U n U t ;
β
1, если U n U t .

54. АЦП последовательных приближений

0000
0000
0001
0001
0000
0010
0010
0010
0011
0011
0000
0100
0100
0100
0101
0101
0100
0110
0110
0110
0111
0111
0000
1000
1000
1000
1001
1001
1000
1010
1010
1010
1011
1011
1000
1100
1100
1100
1101
1101
1100
1110
1110
1110
1111
1111

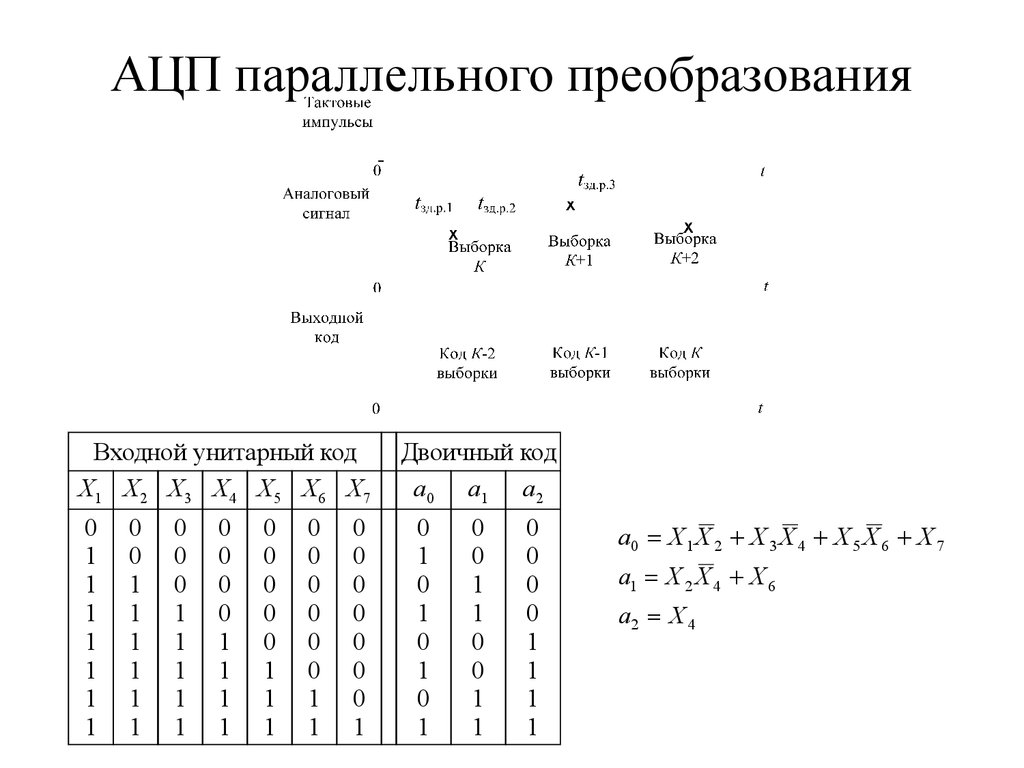
55. АЦП параллельного преобразования

N = 2n-1

56. АЦП параллельного преобразования

Входной унитарный код
Х 1 Х2 Х3 Х 4 Х5 Х6 Х 7
0
1
1
1
1
1
1
1
0
0
1
1
1
1
1
1
0
0
0
1
1
1
1
1
0
0
0
0
1
1
1
1
0
0
0
0
0
1
1
1
0
0
0
0
0
0
1
1
0
0
0
0
0
0
0
1
Двоичный код
а0 а1 а2
0
1
0
1
0
1
0
1
0
0
1
1
0
0
1
1
0
0
0
0
1
1
1
1
a0 X 1 X 2 X 3 X 4 X 5 X 6 X 7
a1 X 2 X 4 X 6
a2 X 4

57. АЦП с двойным интегрированием

58. АЦП с двойным интегрированием

1 t
1 t
U t dt
U оп dt 0.
RC t
RC t
1
2
0
1
t1 t0 =Т0
U t U t
U t T0 U опTх .
T0 N1 / f ; Tх N 2 / f
U t U оп N 2 /N1.
Таким образом, величина выходного сигнала
пропорциональна числу импульсов N2.

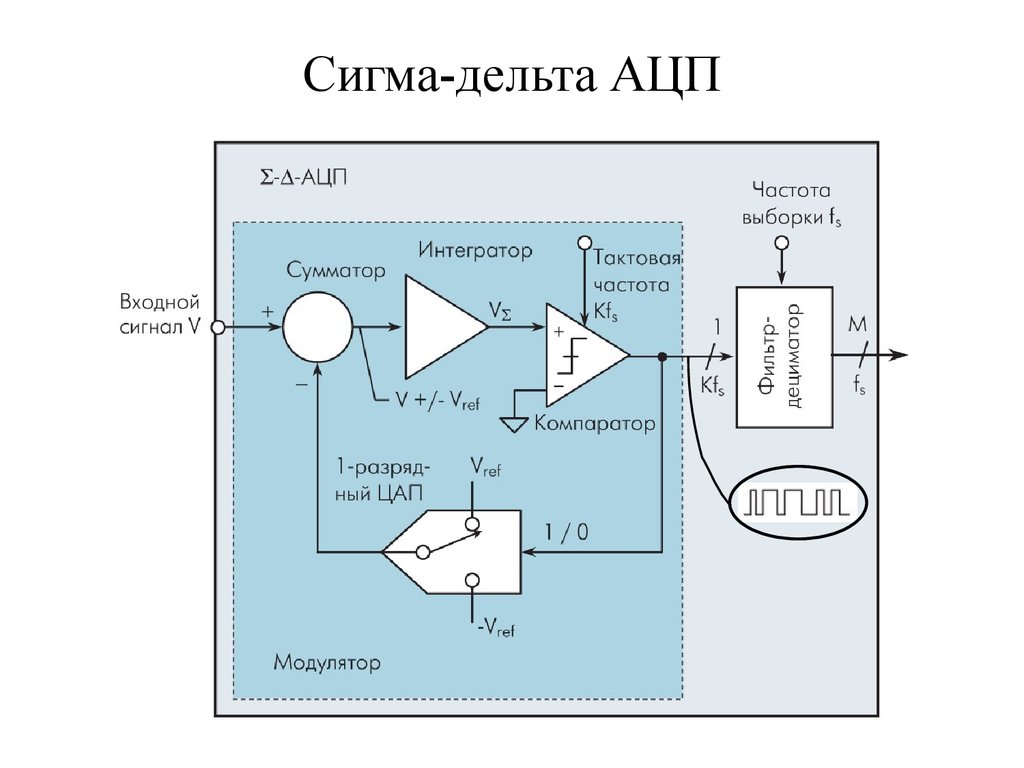
59. Сигма-дельта АЦП

60. Сигма-дельта АЦП

Рассмотрим для Uвх = 0.6 В:
N такта US, В Uи, В Uк, бит
UЦАП, В
1
0,6
0,6
1
1
2
-0,4
0,2
1
1
Перед началом вычисления новой выборки
3
-0,4
-0,2
0
-1
напряжения на выходе интегратора (Uи) и на выходе
4
1,6
1,4
1
1
ЦАП (UЦАП) равны нулю. Сигнал с выхода
5
-0,4
1,0
1
1
сумматора US поступает на интегратор, где
6
-0,4
0,6
1
1
суммируется с предыдущим значением интегратора
7
-0,4
0,2
1
1
(т. е. для i-ой итерации Uи(i) = Uи (i - 1) + V s ).
8
-0,4
-0,2
0
-1
В начальный момент входной сигнал U без
изменений поступает на интегратор.
Компаратор сравнивает выходное значение интегратора Uи с уровнем “0” и выдает 1,
если Uи ≥ 0, и 0 при Uи < 0. Сигнал с компаратора поступает в выходной регистр,
образуя последовательность одноразрядных цифровых отсчетов (выборка модулятора).
Также этот сигнал попадает в ЦАП, который в зависимости от его уровня выдает Uref
или - Uref . В сумматоре это значение вычитается из входного сигнала U и складывается с
Uи в интеграторе. После чего процесс многократно повторяется.

61. Сигма-дельта АЦП

Если U = - Uref, выходная последовательность будет состоять 000000…, а если U =
Uref – 111111… При U = 0 на выходе компаратора будет 101010...
Математически механизм работы модулятора можно представить следующим
образом. Пусть значение Uи в ходе преобразования k раз было меньше “0” и n раз
больше или равным нулю; то общая длина кодовой последовательности для одной
выборки: N = n + k.
Очевидно, что Uи(N) = U + n(U - Uref) + k(U + Uref); Uи(0) = U.
Предположим, что через какое-то число итераций N ≠ 0 напряжение на интеграторе
вновь принимает исходное значение: Uи (N) = U.
Тогда можно записать: U = U (1 + n + k) + Uref (k - n);
Uи = Uref (n - k) / (n +k) = Uref (2n / N - 1).
Таким образом, отношение числа единиц к общей длине циклической
последовательности n/N определяет измеряемое напряжение U как часть диапазона
измерений Uref .

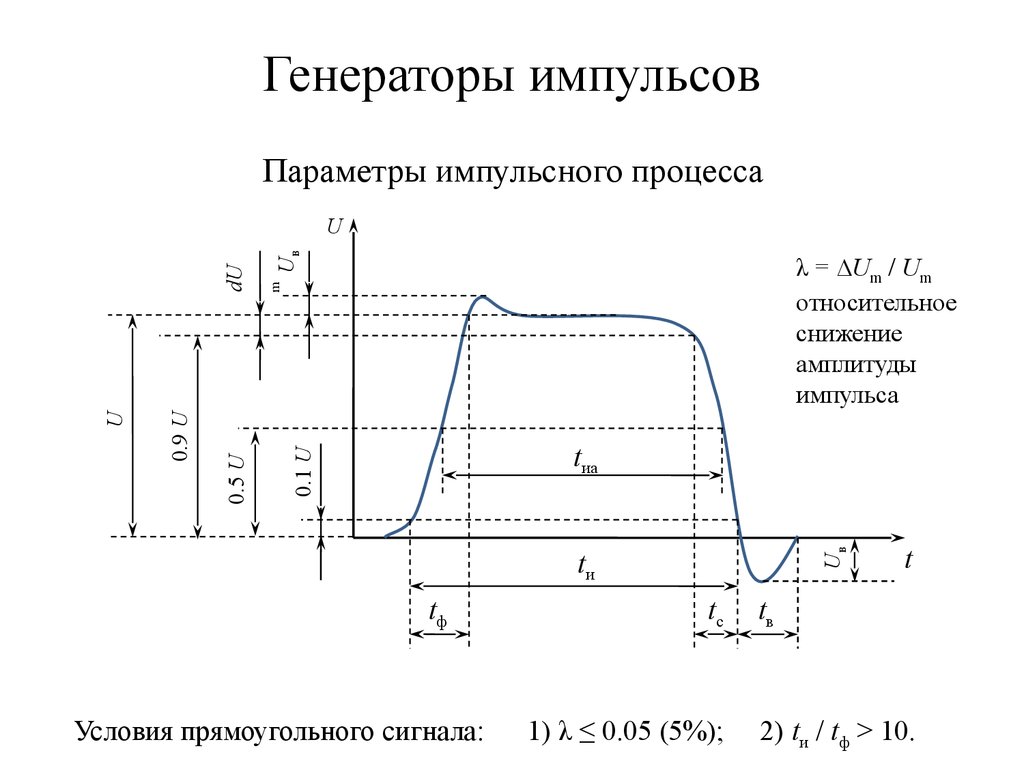
62. Генераторы импульсов

Параметры импульсного процесса
Uв
m
λ = ∆Um / Um
относительное
снижение
амплитуды
импульса
Uв
tиа
0.1 U
0.5 U
0.9 U
U
dU
U
tи
tф
Условия прямоугольного сигнала:
tс
1) λ ≤ 0.05 (5%);
t
tв
2) tи / tф > 10.

63. Параметры импульсного процесса

Сигнал — физический процесс, несущий информацию. По природе
физического процесса делятся на электромагнитные, в частности
электрические (телефония, радио, телевидение, мобильная связь, ЛВС,
Интернет), световые (оптоволоконный кабель), звуковые (общение
людей), пневматические и гидравлические (определенные отрасли
автоматики)и др.
Параметры периодической последовательности импульсов:
– Т
период повторения импульсов;
– f=1/T
частота повторения импульсов;
– Q = T / tи
скважность импульсов;
– Kз = 1 / Q = tи / T
коэффициент заполнения.

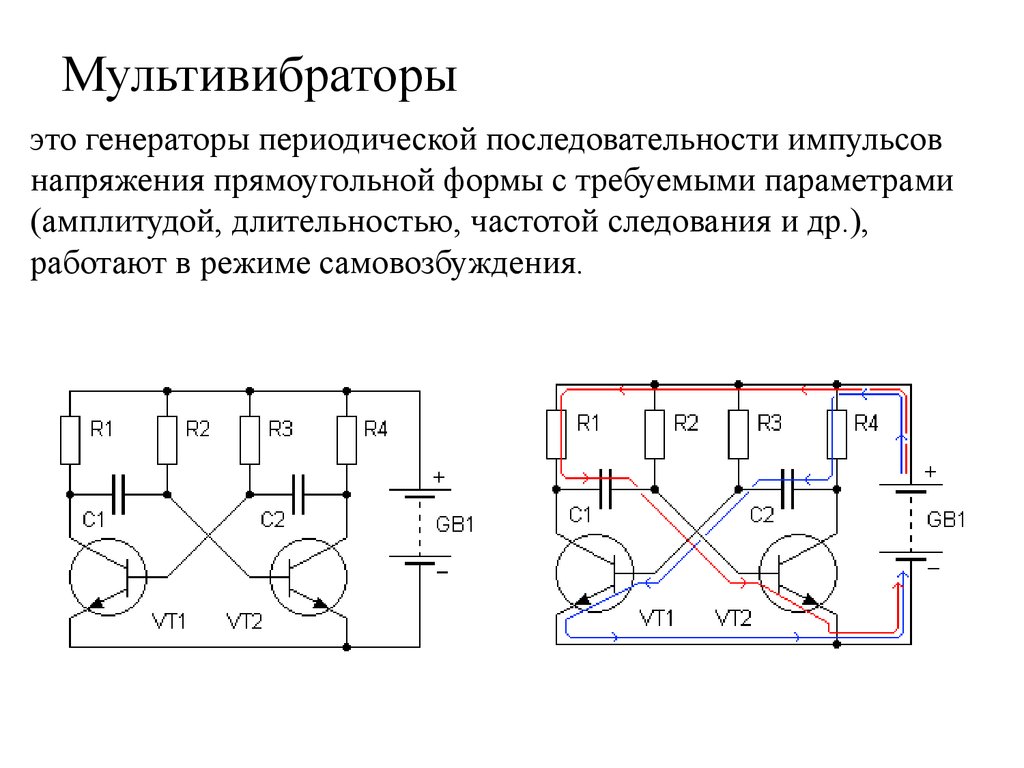
64. Мультивибраторы

это генераторы периодической последовательности импульсов
напряжения прямоугольной формы с требуемыми параметрами
(амплитудой, длительностью, частотой следования и др.),
работают в режиме самовозбуждения.

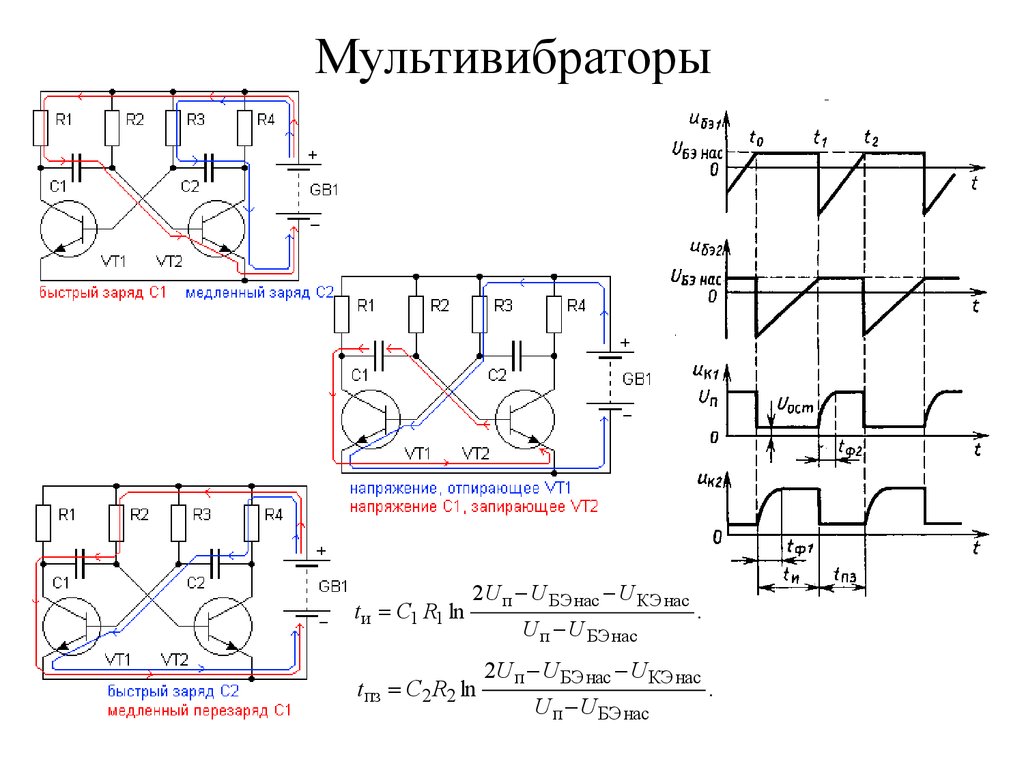
65. Мультивибраторы

tи C1 R1 ln
2 U п U БЭ нас U КЭ нас
tпз C2 R2 ln
U п U БЭ нас
.
2U п U БЭ нас U КЭ нас
U п U БЭ нас
.

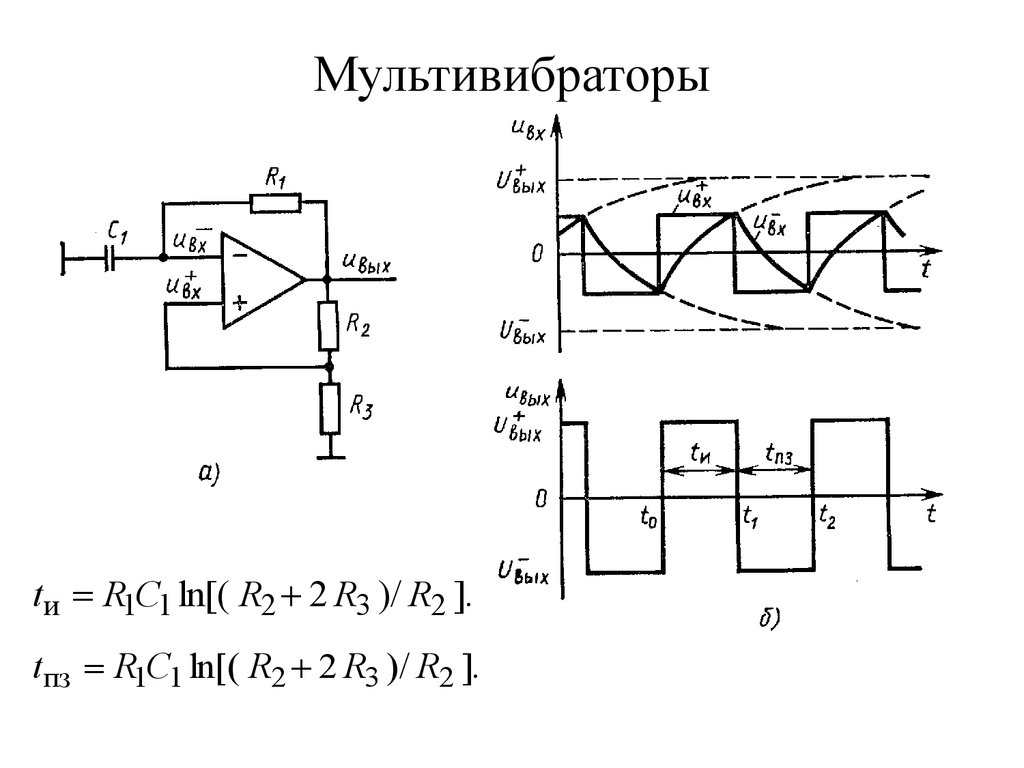
66. Мультивибраторы

tи R1С1 ln[( R2 2 R3 )/ R2 ].
tпз R1С1 ln[( R2 2 R3 )/ R2 ].

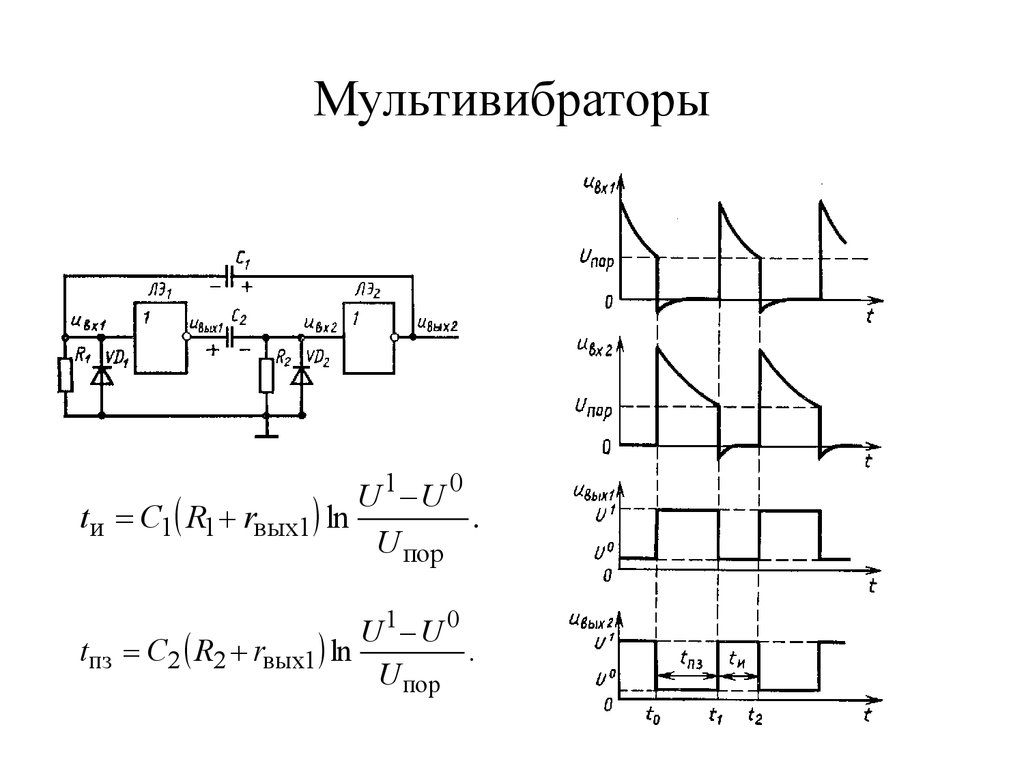
67. Мультивибраторы

U 1 U 0
tи C1 R1 rвых1 ln
.
U пор
U 1 U 0
tпз C2 R2 rвых1 ln
.
U пор

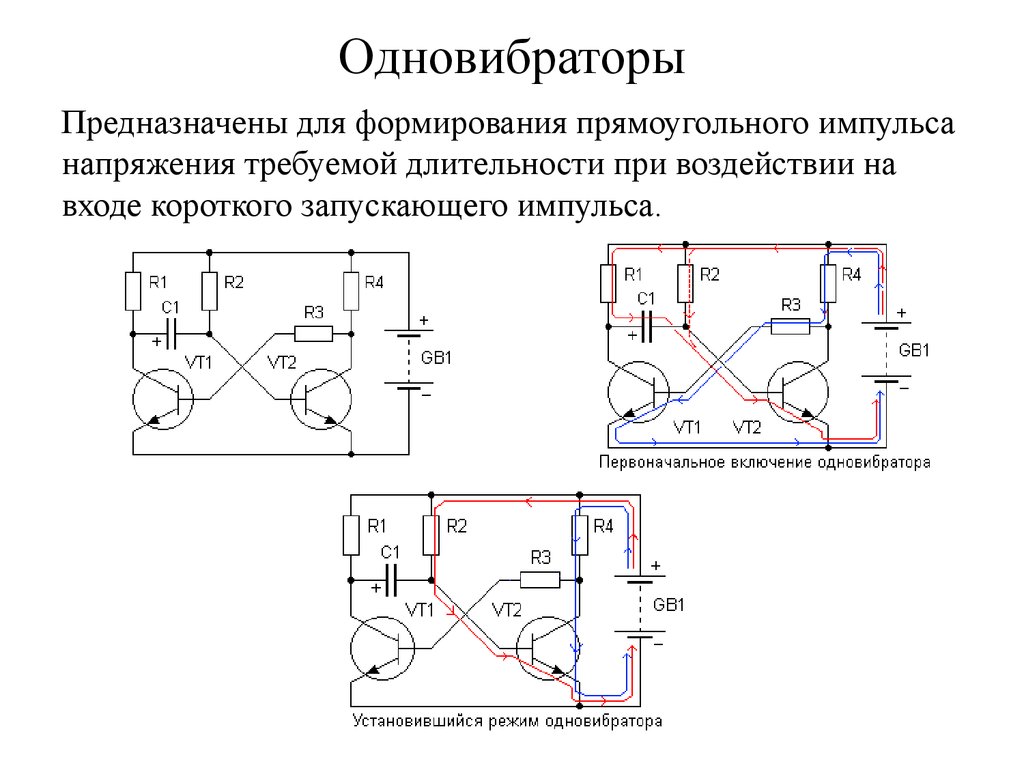
68. Одновибраторы

Предназначены для формирования прямоугольного импульса
напряжения требуемой длительности при воздействии на
входе короткого запускающего импульса.

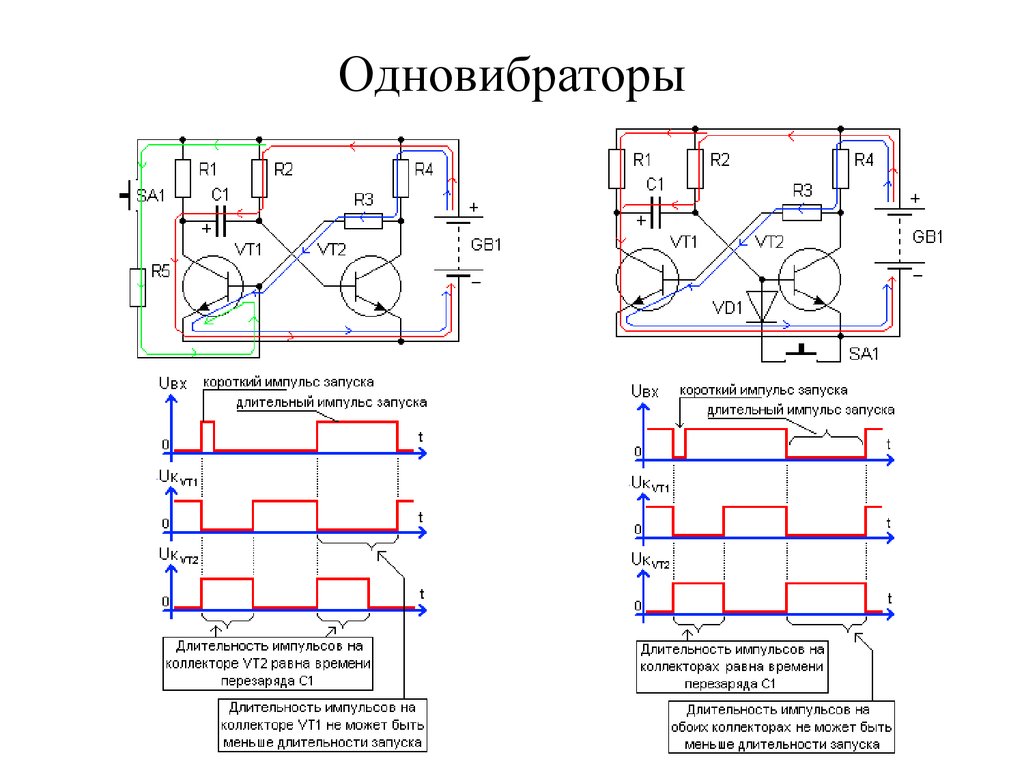
69. Одновибраторы

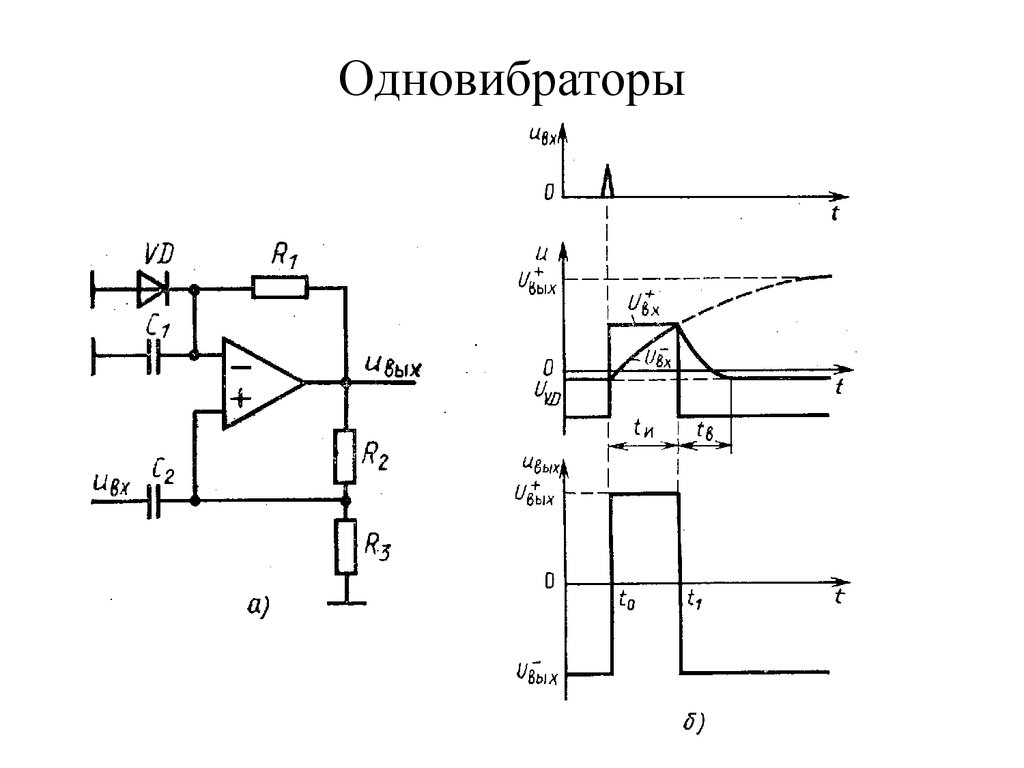
70. Одновибраторы

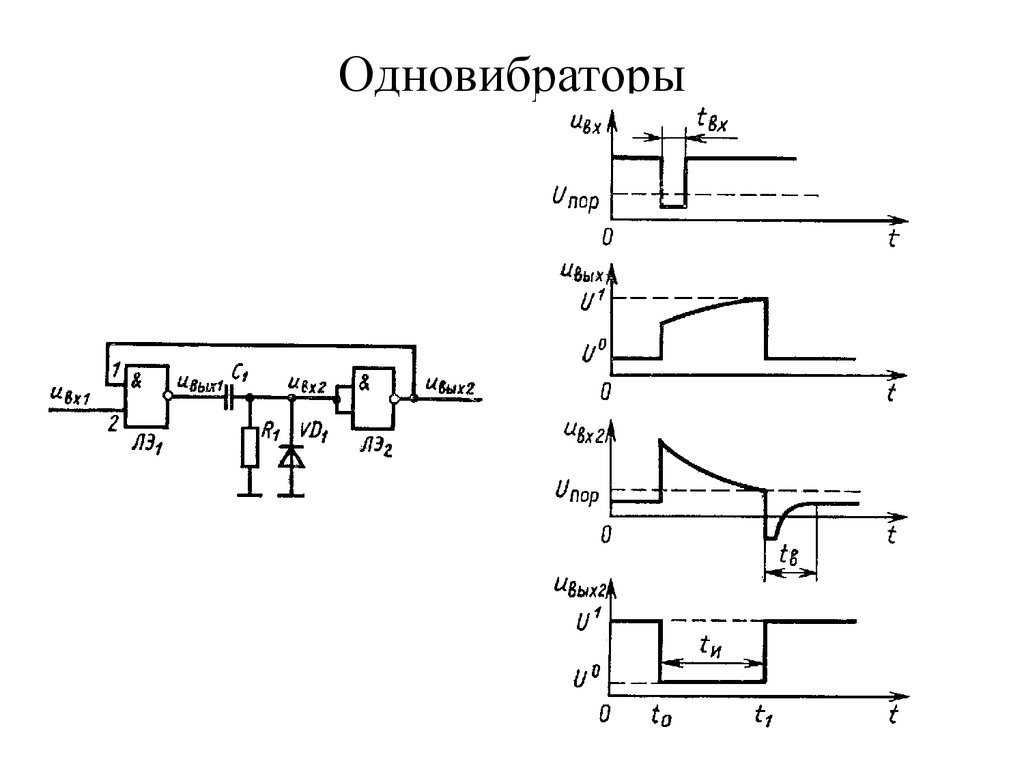
71. Одновибраторы

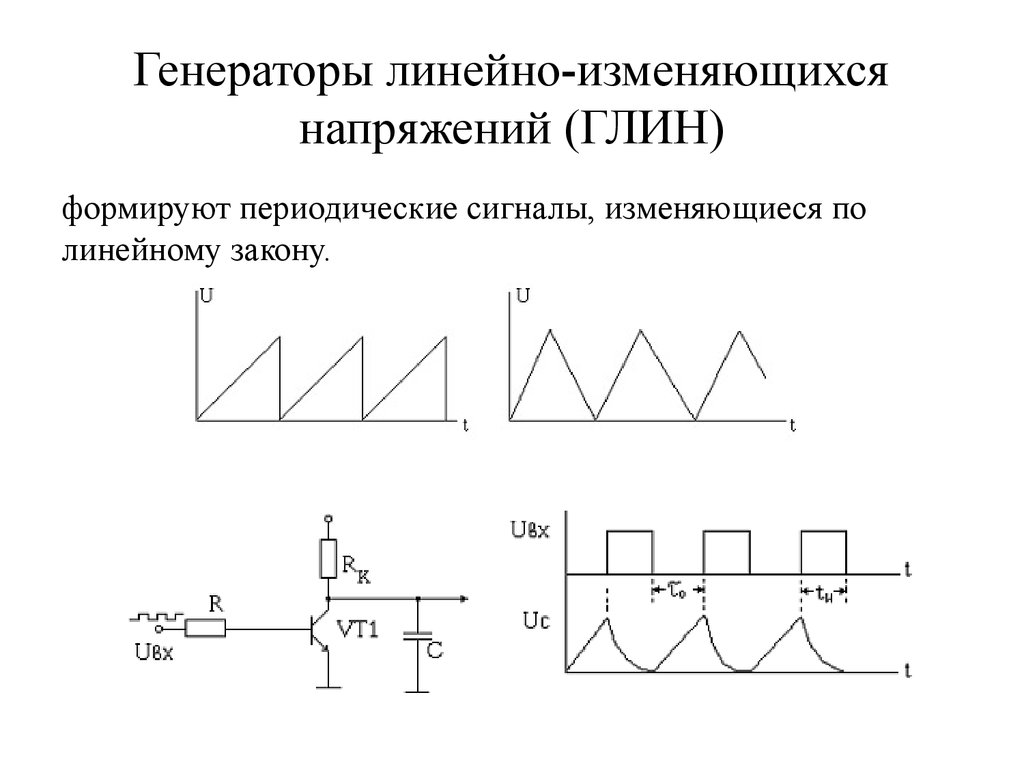
72. Генераторы линейно-изменяющихся напряжений (ГЛИН)

формируют периодические сигналы, изменяющиеся по
линейному закону.

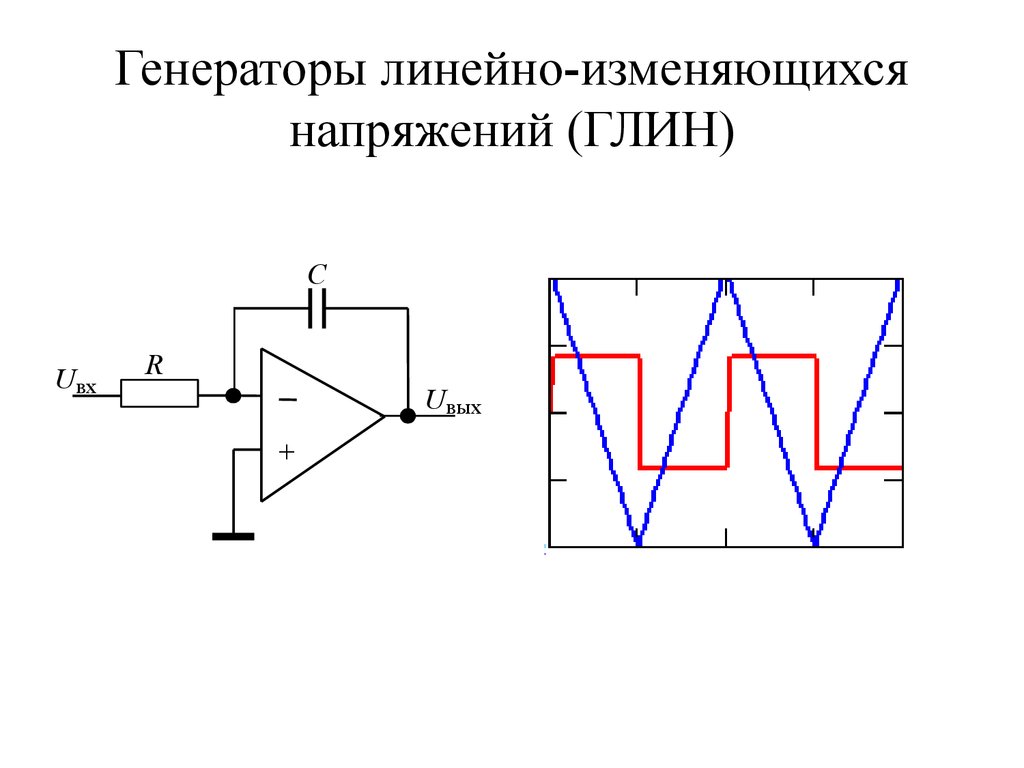
73. Генераторы линейно-изменяющихся напряжений (ГЛИН)

С
Uвх
R
Uвых
+