Похожие презентации:
Симметрия в пространстве. Уравнение Сферы
1. Уравнение Сферы
2.
ОкружностьОкружность – геометрическая фигура,
состоящая из множества точек
плоскости, равноудалённых от данной
точки.
Примеры
Сфера
Сферой называется поверхность,
состоящая из всех точек пространства,
расположенных на данном расстоянии от
данной точки.
Примеры
3.
RА
О
т.О – центр сферы;
R – радиус сферы;
АВ – диаметр сферы – отрезок,
В
соединяющий две точки сферы и
проходящий через её центр.
А, В – диаметрально противоположные
точки шара.
http://lapinagv.jimdo.com/
4.
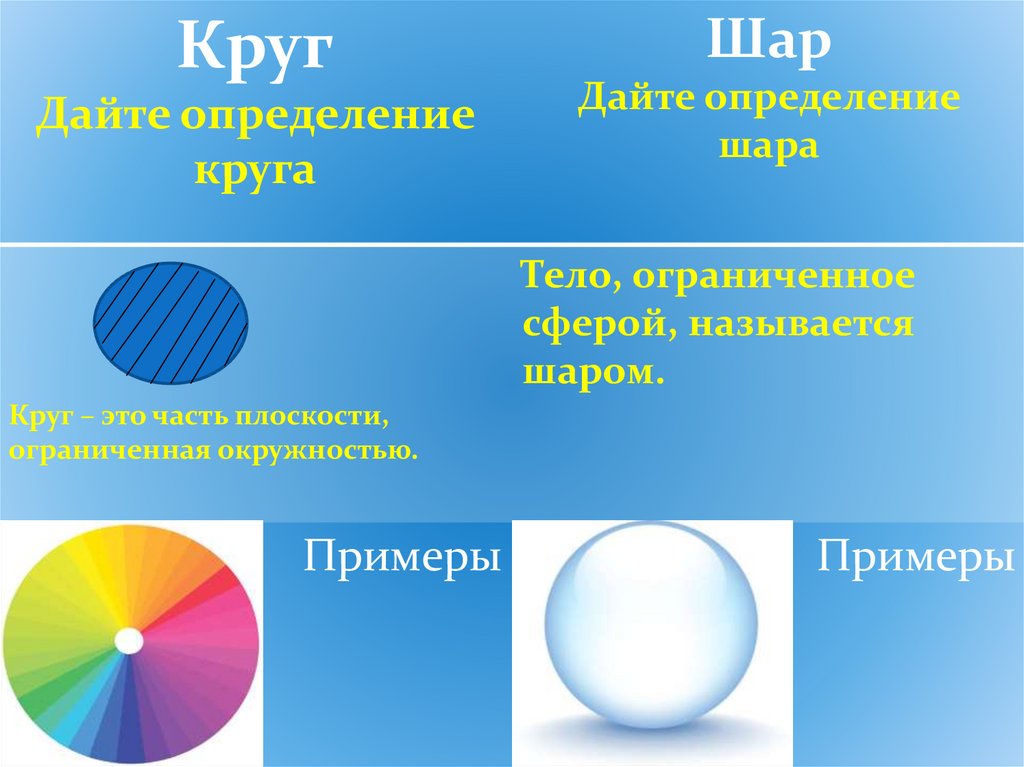
КругДайте определение
круга
Шар
Дайте определение
шара
Тело, ограниченное
сферой, называется
шаром.
Круг – это часть плоскости,
ограниченная окружностью.
Примеры
Примеры
5.
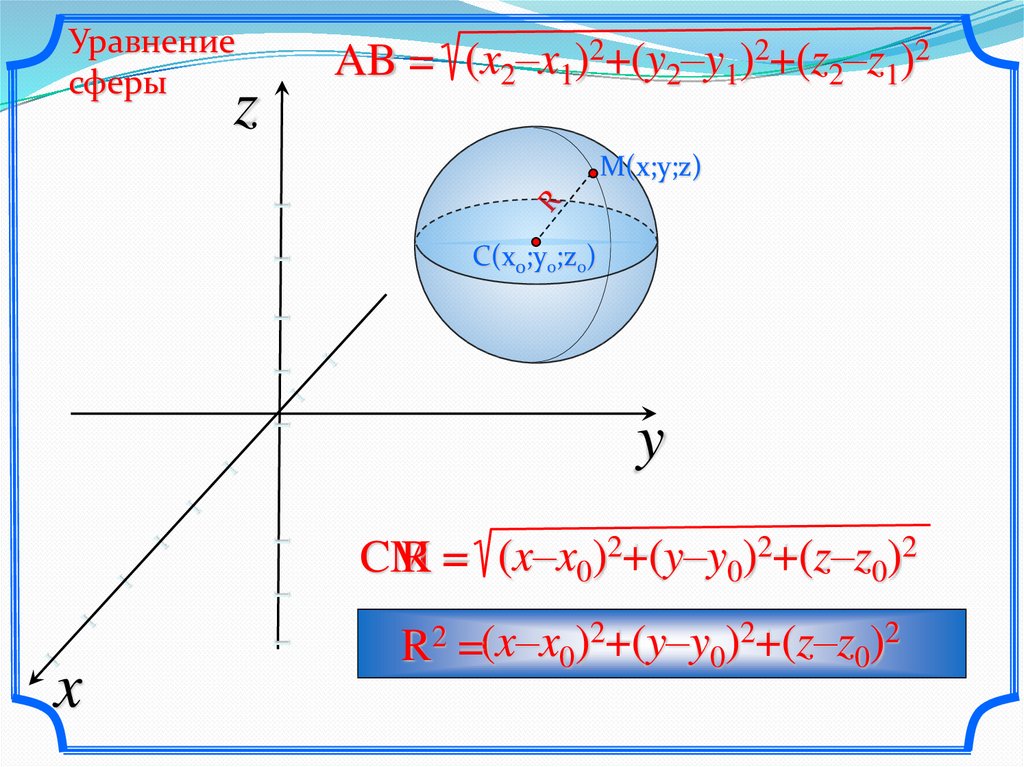
Уравнениесферы
AB = (x2–x1)2+(y2–y1)2+(z2–z1)2
z
C(x0;y0;z0)
y
R = (x–x0)2+(y–y0)2+(z–z0)2
CM
I
I
I
I
I
I
I
I
M(x;y;z)
x
R2 =(x–x0)2+(y–y0)2+(z–z0)2
6. Вывести уравнение сферы с центром в начале координат
x²+y²+z²=R²7.
Уравнение сферыЦентр
r
(x–3)2 +(y–2)2 +(z – 1)2=16 C(3;2;1)
r=4
(x–1)2+(y+2)2+(z+5)2 = 4
C(1;-2;-5)
r=2
(x+5)2+(y–3)2 + z2 = 25
C(-5;3;0)
(x – 1 )2 + y 2 + z 2 = 8
C(1;0;0)
r=5
r= 8
x2 +(y+2)2 +(z+8)2 = 2
C(0;-2;-8)
C(0;0;0)
r= 2
r=3
x 2 + y 2 + z 2= 9
(x–3 )2+(y–2)2 + z 2 = 0,09
C(3; 2;0)
(x+7)2+(y–5)2 +(z+1)2 = 2,5 C(-7; 5;-1)
1
2
2
2
C(0;-4;9)
x +(y+4) + (z+4) = 64
r = 0,3
r = 2,5
5
r= 2





 Математика
Математика








